Vorlesungsmanuskript ET-EW 2011.pdf - von Prof. Dr.-Ing. H. Alt, FH ...

Energietechnik – Energiewirtschaft 

Aachen Fach Nr. 55610, Jülich 1515 

Vorlesungsmanuskript 

Inhaltübersicht der Vorlesung in Stichworten: 

• Elektrische Energieerzeugungssysteme 

- Stoffliche Umwandlungsarten (chem. und kerntechnische) 

- CO2 Emission bei Kohle- und Gasverbrennung 

- Hauptsätze der Thermodynamik 

- Dampfkraftwerksprozesse: Kohle und Kernenergie 

- GuD - Anlagen, BHKW's, Brennstoffzellen 

- Regenerative Energieerzeugung (Wasser, Wind, Sonne, Biomasse) 

- Leistungs-Frequenzregelung 

- Leistungsaustausch in Verbundsysteme, UCTE 

- Verfügbarkeit, Erzeugungsprofil und Lastprofil 

• Energiewirtschaftsgesetz, EU – Richtlinie 

- Stromerzeugungskosten, Leistungs- und Arbeitspreise 

- Wirtschaftlichkeitsberechnung, Annuität 

- Liberalisierter Strommarkt, Undbundling, 

- Strombörse, Stromhandel, Strompreisbildung 

- EEG, KWK-Gesetz, BNA, Emissionshandel 

- Strommix, -Kosten und -Preise 

- Netznutzungsentgelte 

- Kundenwechselprozesse 

- Stromkosten, Stromtarife 

• Elektrische Energieverteilungssysteme 

- Netzebenen und Netzkosten, TSO, DSO 

- AC, DC Übertragungssysteme HDÜ, HGÜ 

- Versorgungsqualität 

- Netzberechnungen, Strahlen-, Ring-, und Maschennetze 

- Lastflussberechnungen, Praktiker-, Knotenpunkt-Potenzial-Verfahren 

- Kurzschlussstromberechnungen 

• Energieanwendungen 

- Strom und Spannungsverhältnisse beim Reihenschwingkreis 

- Oberschwingungsentstehung und –belastung 

- Wechselstromleistung nicht sinusförmiger Ströme 

- Steinmetzschaltung 

- Kraftwirkungen im elektromagnetischen Feld 

- Transformatoren 

- Elektrische Maschinen, Drehstrom und Gleichstrom 

Prof. 

Dr.-Ing. H. Alt 

Stand 30.1.2011

2 

1. Stoffliche Umwandlungsarten zur elektrischen Energieerzeugung 

1.1 Chemische Umwandlungsprozesse 

1.1.1 Kohleverbrennung (Oxidation des Kohlenstoffs, Prozesstemperatur 525 °C bis 700 °C) 

C + O2 ⇒ CO2 + 393 kJ/12g C thermische Energie 

Atomgewichte: 12 + 32 = 44 

Daraus folgt: 

1kg C ergibt 1000g 

393kWs 

kWh 

W = ⋅ = 9, 

10 bei 

44 

GCO 2 = kg = 3, 

67kg 

CO2 

12g 

s kg C 

12 

3600 

h 

Die energiebezogene CO2-Emission beträgt somit: 

kg CO2 

3, 

67 

kg C g CO2 

gCO2 = 

= 403 

kWh kWh 

9, 

1 

kg C 

Für Steinkohle gilt: C + O2 ⇒ CO2 + 8,14 kWh/kg Kohle 

Die CO2 Emission bei der Stromerzeugung mit η= 50 % beträgt 900 g/kWh 

1.1.2 Erdgasverbrennung (Oxidation des Kohlenstoffs und Wasserstoffs, 

Prozesstemperatur 800 °C) 

CH4 + 2 O2 ⇒ CO2 + 2 H2O + 886 kJ/16g CH4 therm. Energie 

Atomgewichte: 16 + 64 = 44 + 36 

1kg CH4 ergibt W 

1000g 

886kWs 

kWh 

⋅ = 15, 

38 

16g 

s kg CH 

3600 

4 

h 

44 

GCO 2 = kg = 2, 

75kg 

CO 

16 

Mit der Dichte von CH4: 

kg 

CH 0, 

72 

4 3 

m 

= ρ folgt: WV kWh 

= W ⋅ ρ CH = 11, 

1 

4 3 

m 

Die energiebezogene CO2-Emission beträgt somit: 

kg CO2 

2, 

75 

kg CH 4 

gCO2 = 

kWh 

15, 

38 

kg CH 4 

g CO2 

= 178, 

8 

kWh 

Für Erdgas gilt: CH4 + 2 O2 ⇒ CO2 + 2 H2O + 11,0 kWh/m 3 CH4 

Die CO2 Emission bei der Stromerzeugung mit η= 50 %: 393 g/kWh 

D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc 

= bei 2 

1.1.3 Brennstoffzelle (umgekehrte Elektrolyse, "kalte Verbrennung", Oxidation des Wasserstoffs 

in einer PEM - Zelle (Proton Exchange Membran), Prozesstemperatur 80 °C) 

2 H2 + O2 ⇒ 2 H2O + 572 kJ/4g H2 therm. Energie 

1kg H2 ergibt: 1000g 

572kWs 

kWh 

W = ⋅ = 39, 

72 ohne CO2-Emission 

4g 

s kg H 

3600 

2 

h 

Mit der Dichte von H2: 

kg 

kWh 

ρ CH = 0, 

0899 folgt: W 3, 

57 

4 

3 

V = W ⋅ ρ CH = 4 

3 

m 

m 

Atomgewichte: 4 + 32 = 36 

Für Wasserstoff gilt: 2 H2 + O2 ⇒ 2 H2O + 3,5 kWh/m 3 H2 

Positive Wasserstoffionen H + (Protonen) wandern in der Zelle durch eine gasdichte Elektrolytmatrix 

von der Anode (Wasserstoffzufuhr mit der Anodenreaktion: H2 - 2e - = 2H + ) zur Kathode 

(Sauerstoffzufuhr mit der Kathodenreaktion: 2H + + 2e - + 1/2 O2 = H2O). Der Ladungsausgleich 

erfolgt im äußeren Stromkreis durch einen Elektronenfluss von der Anode zur Kathode entsprechend 

einem elektrischen Stromfluss von der Kathode (+ Pol) zur Anode (- Pol). An der Kathode 

wird Wasser als Reaktionsprodukt abgeführt. (Zellenspannung 1,23 V). Die langfristige Funktionstüchtigkeit 

der Zelle erfordert sehr reinen Wasserstoff. 

Für stationäre Anwendungen SOFC (Solid Oxide Fuel Cell) mit keramischem Elektrolyt (O 2- Ionen, 

die von der Kathode zur Anode wandern) und einer Prozesstemperatur von 900 °C.


Brennstoffzellen „Elektroden - Reaktionen“ 

SOFC: Kathode: 

Anode: 

Gesamtreaktion: 

MCFC: Kathode: 

Anode: 


PAFC, PEMFC: Anode: 

Kathode: 


AFC: Kathode: 

Anode: 


3 

O2 + 2e - ⇒ O2 - 

O2 - + 2 H2 - 2e - ⇒ 2H2O 

2H2 + O2 ⇒ 2H2O + 572 kJ 

CO2 + ½O2 + 2e - ⇒ CO3 2- 

CO3 2- + H2 - 2e - ⇒ H2O + CO2 

H2 + CO2 + ½O2 ⇒ H2O + CO2 

H2 - 2e - ⇒ 2H + 

2H + + 2e - + ½O2 ⇒ H2O 

H2 + ½O2 ⇒ H2O + 286 kJ 

½O2 + 2e - + H2O ⇒ 2OH - 

2OH - + H2 - 2e - ⇒ 2H2O 

2(H2 + ½O2) ⇒ 2H2O + 572 kJ 

572 kJ/Mol = 572 kJ/4gH = 143 kJ/gH = 143 kWs/gH = 39,7 kWh/kg H. Der untere Heizwert von 

Wasserstoff beträgt: 33 kWh/kg, von Methan 13,9 kWh/kg und von Benzin 12,4 kWh/kg. 

Das spezifische Gewicht (Wichte) des Wasserstoffs H unter Normalbedingungen (d.h. 0°C, 760 

mm QS) ist 0,09 kg/m 3 . 

Dem unteren Heizwert von 33 kWh/kg entspricht somit 3 kWh/m 3 , so dass für die exotherme 

Wasserstoff - Sauerstoff - Redaktion gilt: 

H2 + ½ O2 ⇒ H2O + 3 kWh/m 3 (Hu) 

Zum Vergleich: Erdgasverbrennung (CH4) ergibt 11,3 kWh/m 3 . Ohne katalytische Verluste ergeben 

sich somit einschließlich der Konvertierung und Reformierung des Erdgases rd. 3 kWh elektrische 

Energie und 8 kWh Wärmeenergie. In der Praxis ist dieses Verhältnis elektrische zu thermische 

Energie bei Reformierung des Erdgases CH4 mit Wasserdampf zu H2 und CO2 etwa 1:3. 

Strukturvielfalt der Kohlen- 

Wasserstoff-Verbindungen: 

Netzstruktur 

Linearstruktur 

Zentralstruktur 

Atombindung 

Abkürzungen und Brennstoffzellenarten: 

SOFC: Solid Oxide Fuel - Cell, Elektrolyt: Keramik (dotiertes Zirkonoxyd) 

MCFC: Molten Carbonate Fuel - Cell, Elektrolyt: Karbonatschmelze 

PAFC: Phosphoric Acid Fuel - Cell, Elektrolyt: H3PO4 

(ortho - Phosphorsäure) 

PEMFC: Proton Exchange Membran Fuel - Cell, Elektrolyt: 

DMFC: Direct Methanol Fuel - Cell, Polymermembran 

(2CH3OH + 4H2O → 5H2 + 2H2O + 2CO2) 

AFC: Alcaline Fuel - Cell, Elektrolyt: KOH (Kaliumhydroxid)

Funktionsweise der Brennstoffzellen – Arten: 

Nicht umgesetzter 

Brennstoff (10-20 %) 

SOFC: Solid Oxide Fuel - Cell, Elektrolyt: Keramik (dotiertes Zirkonoxyd) 

MCFC: Molten Carbonate Fuel - Cell, Elektrolyt: Karbonatschmelze 

PAFC: Phosphoric Acid Fuel - Cell, Elektrolyt: H3PO4 (ortho - Phosphorsäure) 

PEMFC: Proton Exchange Membran Fuel - Cell, Elektrolyt: 

DMFC: Direct Methanol Fuel - Cell, Polymermembran 

(2CH3OH + 4H2O → 5H2 + 2H2O + 2CO2) 

AFC: Alcaline Fuel - Cell, Elektrolyt: KOH (Kaliumhydroxid) 

Erdgas-Brennstoffzelle 

mit Reformer und Konverter: 

Reformer: 

T > 200 °C: 

CH4 + H2ODampf⇒ 3H2+CO - 214 kJ/mol 

Konverter: 

T < 500 °C: 

CO + H2ODampf ⇒ H2+CO2 + 42 kJ/mol 


4 

Elektrischer Strom I 

2 H2O 

SOFC O 2 - O2 O 800-1000 °C 

2- 

2 H2 

CO2 CO2 

MCFC H2O CO3 600-660 °C 

2- 

H2 ½O2 

PAFC H2 160-200 °C 

PEMFC H H2O 60- 80 °C 

DMFC Methanol ½O2 80-110 °C 

+ 

H + 

H2O H2O 

AFC ½O2 60-90 °C 

Brennstoff H2 

H2 

- Pol 

- - 

U 

Zellenspannung < 1 V 

Elektrisches Feld 

E 

OH - OH - 

- - 

+ Pol 

Elektrolyt 

Polymere- 

Membran 

Anode Kathode 

- Anionen 

CH4 

(Erdgas) 

CO2 

Reformer 

und 

Konverter 

+ Kationen 

(Wasserdampf) 

H2O 

H2 

(Wasserstoff) 

Nicht umgesetzter 

Oxidant 

Sauerstoff O2, (Luft) 

CO2 (Oxidant) 

Luft / Sauerstoff 

Brennstoffzelle 

z. B. 

A 

K 

K 

PEM-FC

5 

1.2 Kerntechnische Umwandlungsarten 

Bei kerntechnischen Umwandlungen ist man ins Kleinste „Im Herzen der Materie“ vorgestoßen. 

Lecture room in the Ernest Rutherford museum, 

Arts Centre, Christchurch, Canterbury, New Zealand 

Rutherfords Streuexperiment 

Im Jahr 1911 schossen Rutherfords Team Hans Geiger und Ernest Marsden in einem bahnbrechenden 

Experiment Alphateilchen auf eine dünne Goldfolie und beobachteten zu ihrer Verblüffung, 

dass einige Alphateilchen unter sehr großen Streuwinkeln gestreut wurden, während die 

meisten praktisch ohne Ablenkung durch die Goldfolie flogen. Ein solches Streuexperiment ist im 

Rutherford Museum im Arts Centre, in Christchurch, Neuseeland zu beobachten. Ernest Rutherford 

erklärte diese Beobachtung mit der Annahme, dass Atome aus einem kleinen, positiv geladenen 

Kern bestehen, um den Elektronen kreisen. Im Atomkern wirken sehr starke Kernkräfte der 

Nuklide anziehend, die elektrischen Kräfte jedoch abstoßend, wobei bei engem Kontakt der Nuklide 

die Kernkräfte überwiegen (wie bei klebrigen Bonbons). 

Große Streuwinkel treten demnach auf, wenn die Flugbahn eines positiv geladenen Alphateilchens 

ganz nah an einem Kern vorbeiführt. Dieses Experiment gilt allgemein als Ausgangspunkt für die 

Erforschung des Aufbaus der Materie. 

Später stellte sich heraus, dass der Kern aus positiv geladenen Protonen und elektrisch neutralen 

Neutronen besteht. Die Annahme, dass diese Bestandteile punktförmig seien, ließ sich jedoch 

nicht lange halten. 1956 führte Robert Hofstadter weitere Streuexperimente durch, nun mit Elektronen 

an Protonen, deren Ergebnisse sich bei ausreichend hoher Energie der Elektronen nicht 

mehr durch die Rutherfordsche Streuformel beschreiben ließen. Eine Erklärung war jedoch möglich 

unter der Annahme, dass die Ladung des Protons nicht in einem Punkt konzentriert ist. 

Die höhere Energie war entscheidend - sie ermöglichte das „Abtasten“ des Protons mit hinreichend 

guter Auflösung, sodass sich dessen ausgedehnte Natur offenbarte. 

Ende der Sechzigerjahre schließlich führten Jerome Friedman, Henry Kendall und Richard Taylor 

eine Reihe von Experimenten am Stanford Linear Accelerator Center (SLAC) mit Elektronenstrahlen 

von noch höherer Energie durch. Dabei zeigte sich, dass sich das nach Rutherford erwartete 

Verhalten wieder einstellt, wenn man drei punktartige Bestandteile des Protons mit elektronischen 

Teilladungen postuliert - jene Quarks, die Murray Gell-Mann und Georg Zweig vorausgesagt hatten. 

Mit Quarks als Bestandteilen ließen sich die Eigenschaften von Proton, Neutron und viele andere 

Teilchen erklären. 

Aber auch dieses einfache Bild erwies sich als unvollständig: Weitere Experimente am Europäischen 

Laboratorium für Teilchenphysik (CERN) und am Fermi National Accelerator Laboratory 

(FNAL) in den Siebziger- und Achtzigerjahren zeigten, dass die Summe der Impulse der Quarks 

allein nur die Hälfte des Protonimpulses ergab. Den Rest tragen die von der Theorie der starken 

Wechselwirkung, der Quantenchromodynamik (QCD), vorhergesagten Gluonen, mit deren Hilfe 

sich die in verschiedenen Experimenten beobachtete Protonenstruktur erklären lassen. 

Die Wahrscheinlichkeit einer Wechselwirkung bei einem Streuexpereiment wird durch den 

„Wirkungsquerschnitt“, gemessen in barn angegeben (1 barn = 10 -28 m 2 ). 

Quelle:Caldwell, Allen; Grindhammer, Günter: Im Herzen der Materie, Physik Journal 6(2007) S.39-45. 

D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc

6 

1.2.1 Kernspaltung 

Einsteinsche Energie-Masse-Relation 

In der Physik ist beim Aufbau der Materie das Ganze weniger als die Summe seiner Teile. 

Dies hat mit der so genannten Bindungsenergie zu tun. 

Dass ein Element "stabil" ist, heißt nichts anderes, als dass es nicht einfach so im Laufe der Zeit 

spontan in seine Einzelteile, den Nukliden, zerfällt. Ein Helium-Atomkern beispielsweise zerfällt 

nicht einfach in die zwei Protonen und zwei Neutronen, aus denen er zusammengesetzt ist. 

Um einen stabilen Atomkern in seine Bestandteile zu zerlegen, ist ein energetischer Aufwand nötig, 

es muss Energie aufgewandt werden um etwa die Nuklide auseinander zuziehen und dabei die 

Kräfte überwinden, die sie zusammenhalten. Energie kann nun aber nicht aus dem Nichts entstehen 

oder verschwinden. In der Energiebilanz für die Zerlegung eines Atomkerns in seine Einzelteile, 

muss daher auch die Energie auftauchen, die für die Zerlegung aufgewandt werden muss: 

Energie des gebundenen Systems + aufgewendete Energie = Summe der Energien der Einzelteile 

oder, wenn man die aufzuwendende Energie auf die rechte Seite der Gleichung hinüberbringt, 

Energie des gebundenen Systems = Summe der Energien der Einzelteile - zur Trennung aufzuwen-dende 

Energie. Energetisch ist das gebundene System damit weniger als die Summe seiner 

Teile. 

Die "zur Trennung aufzuwendende Energie" wird auch Bindungsenergie EB genannt: 

2 

2 

≈ ∆m 

⋅ c , = ( M − Z ⋅ M − N ⋅ M ) ⋅ c 

EB EB K 

P 

N 

mit MK : Kernmasse, Mp : Protonmasse, Mn : Neutronmasse 

Mit Einsteins berühmter Äquivalenz von Energie und (relativistischer) Masse E = ∆m·c 2 entspricht 

jeder Energie eine Masse und jeder Masse lässt sich eine Energie zuschreiben. Die relativistische 

Masse des gebundenen Systems ist daher etwas kleiner als die Summe der Massen der Einzelteile, 

nämlich: 

Masse des gebundenen Systems = Summe der Massen der Einzelteile - Bindungsenergie/c 2 . 

Ein Heliumatomkern aus zwei Protonen und zwei Neutronen hat beispielsweise etwas weniger 

Masse als zweimal Protonenmasse plus zweimal Neutronenmasse. Die Differenz, der so genannte 

Massendefekt, ist ein Maß für die Bindungsenergie und damit dafür, wie stark die Bindung der vier 

Kernteilchen aneinander ist: Je größer die Energie, die zur Zerlegung aufgewendet werden muss, 

umso stärker die Bindung (wie bei klebrige Bonbons). Für chemische Bindungen, mit Bindungsenergien 

von bis zu wenigen eV, wie sie die Atome und Moleküle der uns umgebenden Materie 

zusammenhalten, ist der Massendefekt freilich unmessbar klein. Typische Massendefekte liegen 

bei Hunderttausendsteln oder Millionstel der Masse eines Elektrons (man spricht hier von starker 

bzw. schwacher Wechselwirkung). 

Anders bei den Bindungsenergien der Kernkräfte, die die Protonen und Neutronen eines Atomkerns 

zusammenhalten. Sie sind millionen- bis milliardenfach größer. Massendefekte bei Atomkernen 

entsprechen den Massen einiger Dutzende bis Hunderte von Elektronen. Solche Massenunterschiede 

sind bei Atomkernen tatsächlich mit großer Genauigkeit messbar (man sagt hier starke 

Wechselwirkung). 

Kr 

Krypton 

Sehr stabile 

Kerne 

Ba Barium 


Kernspaltung 

(200 MeV bei 

Massenzahl 235) 

T Tritium 

Kernfusion (17,6 MeV, bei Massenzahl 4) 

D Deuterium 

Jeder der rund 2.000 Punkte entspricht 

einer bestimmten Sorte 

Atom (115 Elemente und Isotope 

der Elemente). 

Auf der Ordinatenachse ist die 

Bindungsenergie in MeV pro 

Kernteilchen aufgetragen. Sie ist 

ein Maß dafür, wieviel Energie 

man aufwenden muss, um ein 

Proton oder Neutron aus dem 

Atomkern herauszulösen. 

Definiert ist diese Einheit als die 

Energie, die ein Elektron gewinnt, 

wenn es eine elektrische Spannungsifferenz 

von einer Million

7 

Volt durchläuft. 1 MeV entspricht in etwa der doppelten Masse eines Elektrons. 

Die Einsteinsche Energie-Massenrelation bedeutet keine Umrechnung von Masse in Energie, sondern 

beschreibt die relativistische Masse und Bindungsenergie der Nuklide. (Otter/Honecker, Bd.II, 

S.257) 

Energiebilanz und Massenumwandlung bei der Kernspaltung 

Eine von vielen im Kernreaktor ablaufende Kernspaltungsreaktionen des Uransisotops 235 ist 

z.B.: 

1 97 137 

1 

U + o n → Kr + Ba + n + Energie 

235 

92 36 56 2 0 

(200 MeV) 

Die Summe der Masse der 92 Protonen und 143 Neutronen des 235 U beträgt einzeln 236,91 AME. 

Die Basiseinheit der Stoffmenge ist das Mol. 1 Mol ist die Stoffmenge eines Systems, das aus 

ebensoviel Einzelteilchen besteht, wie Atome in 12 g des Kohlenstoffnuklids 12 C enthalten sind. 

Seit den Arbeiten von Amadio Avogadro (1776-1856) ist die Zahl der Teilchen in einem Mol bekannt: 

In einem Mol Kohlenstoff (12g) sind es 6,022045 . 10 23 Teilchen (Avogadrosche Zahl, 

Loschmidtsche Zahl, NA). Die Atommasseneinheit AME entspricht der Masse von 1/NA in g: 

1 

-24 

2 

1 AME = g = 1,66 ⋅10 

g = 931 , 5MeV/c 

23 

6, 

022 ⋅10 

Ein Kilogramm U235 ( 1000 g) enthält 6,022·10 26 /235 Kerne, d.h. der Massendefekt bei der Spal- 

26 

3 

− 24 6, 

022 ⋅10 

0, 

213 ⋅10 

tung von 1 kg U235 ist: ∆m 

= 0, 

213 ⋅1, 

66 ⋅10 

⋅ 

= 

g = 0, 

906 g 

235 235 

Nach der Einsteinschen Energie-Masserelation ergibt sich für die Energieausbeute bei der Spaltung 

1kg U235: 

2 

2 

2 ⎛ 8 m ⎞ 

−3 

16 m 

13 kg ⋅ m 

12 

E = ∆m 

⋅ c = 0, 

906 g ⋅ ⎜3 

⋅10 

⎟ = 0, 

906 ⋅10 

kg ⋅ 9 ⋅10 

= 8, 

154 ⋅10 

= 81, 

54 ⋅10 

Ws 

2 

2 

⎝ s ⎠ 

s 

s 

6 

E = 22, 

65 ⋅10 

kWh thermische Energie je kg U235. 

In einem kg Natururan sind 0,71 % spaltbares Uran 235, somit beträgt der Energieinhalt von 1 kg 

0, 

71 

Natururan: ENatururan = E ⋅ kWh = 160. 

815 kWh 

100 

Im Betrieb eines Kernreaktors wird aus dem nicht spaltbaren U238 durch die Wechselwirkung mit 

den bei der Kernspaltung zunächst vorhandenen schnellen Neutronen in einem Brutprozess spaltbares 

Plutonium 239 und spaltbares Uran 233 gebildet, die dann im weiteren Betrieb des Reaktors 

ebenfalls gespalten werden und zur Energiegewinnung beitragen, so dass die thermische Energieerzeugung 

aus dem Natururan insgesamt rd. 350.000 kWh pro kg beträgt. Bei Kohle beträgt 

die thermische Energie 8,14 kWh. Das nicht im Reaktor selbst gespaltene Plutonium wird bei der 

Wiederaufbereitung der Brennelemente chemisch isoliert und in so genannten Mischoxid- 

Brennelementen (MOX) wieder dem Reaktor zugeführt. 


Baustein Atommasse mK 

Kernart Protonen Neutronen AME 

235 U 92 143 235,125 

1 n 0 1 1,009 

Summe 92 236,134 

Spaltprodukte nach der Kernspaltung: 

137 

Ba 56 81 136,951 

97 Kr 36 61 96,952 

2 1 n 0 2 2,018 

Summe 92 144 235,921 

Massendefekt (Differenz) je Kernspaltung 0,213 

2

8 

1.2.2 Kernfusion 

Kernenergie lässt sich auch über den Aufbau schwerer Kerne aus leichten Kernen (Kernfusionpro- 

2 3 4 1 

zess), gewinnen z. B.: 1 D+ 1T 

⇒2 

He + 0n 

+ ∆E 

, ∆E = 17,6 MeV 

Kernfusion und Kernspaltung lassen sich als Kettenreaktion führen; allerdings wurde bisher nur bei 

der Kernspaltung eine kontrollierte Kettenreaktion verwirklicht. Eine massenkontrollierte Fusionsreaktion 

liefert die Wärme unseres Zentralgestirns, eine unkontrollierte Kernfusions-Kettenreaktion 

erfolgt bei der Explosion einer Wasserstoffbombe. Im Jahr 1991 wurde am Joint European Torus 

(JET) in Culham/England erstmals auch unter irdischen Bedingungen nachgewiesen, dass sich 

eine (D2 + T2)-Mischung auch thermisch in kontrollierter Form „zünden“ lässt. 

Die bei Kernprozessen freiwerdende Energie ∆E tritt – wie dies auch bei chemischen Reaktionen 

der Fall ist – als Massendifferenz zwischen Anfangs- und Endzustand des Systems in Erscheinung 

(Massendefekt). Dieser Massendefekt ∆m ist über die Einstein-Beziehung ∆E = ∆m c 2 einer Energie 

gleich; wobei der Masse 1 AME die Energie 931 MeV entspricht. Die relativen Massendefekte 

∆m/m sind für chemische Reaktionen verschwindend klein. 

Hier wird meist nur die Bindungsenergie der chemischen Bindungen im Bereich von (1 – 5)eV frei. 

Nach den chemischen Reaktionen weisen die radioaktiven Zerfallsprozesse die geringsten Massendefekte 

auf (∆m/m in der Größenordnung von 10 -10 ; 10 Milliardstel), während der Massenverlust 

bei Kernfusion und Kernspaltung (∆m/m in der Größenordnung von 10 -3 ; Tausendstel) mit einer 

guten Waage bestimmt werden könnte. Eine vollständige Massenvernichtung (∆m/m=1!) tritt 

bei Teilchen-Antiteilchen-Reaktionen auf, z. B. bei der Wechselwirkung von Positronen mit Negatronen 

(Paarvernichtung). 

Wird die von einem Radionuklid emittierte Strahlung in der Probe absorbiert, so führt dies in den 

meisten Fällen zu deren Aufheizung (Ausnahme: (a,n)-, (g,n)-Kernreaktionen oder g-Wechselwirkung) 

In den Radionuklid- oder Isotopenbatterien nutzt man den sich somit ausbildenden Temperaturunterschied 

zur Umgebung aus. Bei den heute in Betrieb befindlichen Isotopenbatterien 

wird diese Wärmeenergie über die thermoelektrische Konversion (Seebeck-Effekt) mit einem Wirkungsgrad 

von maximal 3 bis 5 % in elektrische Energie umgewandelt. Eine höhere Ausbeute an 

elektrischer Energie von 8 bis 10 % liefert die thermoionische Anordnung, deren Technologie aber 

noch nicht genügend entwickelt ist. 

Die bei radioaktiven Zerfallsprozessen freiwerdende Energie ist mit weniger als 100 keV/u relativ 

gering. Für Isotopenbatterien mit konstanter, hoher Leistung, aber kleinem Volumen und Gewicht 

werden Radionuklide benötigt, die eine relativ lange Halbwertszeit besitzen, beim Zerfall möglichst 

viel Energie in Freiheit setzen und keine oder nur eine sehr geringe Abschirmung benötigen, um 

eine Strahlenbelastung der Umgebung auszuschließen. 

Vorteilhaft sind daher α-strahlende Nuklide wie 238 Pu, 244 Cm und 210 Po. β-aktive Nuklide wie 144 Ce 

und 90 Sr sind zwar als Abfallprodukte der Kernspaltung billiger, bedürfen aber einer relativ dicken 

Abschirmung. 

Das wichtigste Nuklid für Isotopenbatterien ist 238 Pu, da es mit einer Halbwertszeit von 87,74 Jahren 

beim Zerfall nur α-Strahlen mit 5,5 MeV emittiert und die Zahl der Spontanspaltneutronen wegen 

der langen Spontanspalthalbwertszeit von 238 Pu niedrig ist. 238 Pu wird heute in kg-Mengen 

über die Reaktionen: 

237 Np (n,g) 238 Np -(b - ) → 238 Pu 

und in geringeren Mengen über: 241 Am (n,g) 242 Am -(b - ) → 242 Cm-(a) → 238 Pu gewonnen. 

Durch 237 Np-Bestrahlung erzeugtes 238 Pu besteht zu etwa 80 bis 85 % aus 

238 239 

Pu, zu 10 bis 15 % aus Pu und zu 3 bis 5 % aus höheren Pu-Isotopen. 

Sämtliche im Rahmen des Apollo-Mondlandungsprogramms benutzten Isotopenbatterien 

enthielten 238 PuO2 als Energiequelle (SNAP-27 mit ca. 4 kg 

238 

PuO2 lieferte bei 1480 Wth eine elektrische Leistung von ca. 60 W). 

Seit 1968 beim Absturz nach dem Fehlstart einer Rakete eine ungeschütze 

Pu-Isotopenbatterie in der Erdatmosphäre verglühte, wurde eine 

Wiederholung einer solchen Freisetzung durch entsprechend angebrachte 

Hitzeschilde ausgeschlossen. Für die Erforschung der äußeren 

Planeten unseres Sonnensystems sind Pu-Isotopen-Batterien die 

bisher einzige, zuverlässige Energiequelle. 


100 Watt Pu-238 Quelle, wie sie in einer 

Raumfahrtmission 1970 verwendet worden 

ist. Die Quelle ist 250 g schwer und 

ungefähr 3 cm im Durchmesser. Quelle: 

Los Alamos National Laboratory, U.S.A

9 

2. Thermodynamische Kreisprozesse 

2.1 Hauptsätze der Thermodynamik 

2.1.1 1. Hauptsatz: Energieerhaltungssatz 

Der erste Hauptsatz der Thermodynamik ist aus dem Satz der Energieerhaltung abgeleitet: 

Jedes abgeschlossenen System besitzt eine innere Energie U (= extensive Zustandsgröße). 

Diese kann sich nur durch den Transport von Energie in Form von Wärme Q Und/oder 

von technischer Arbeit Wt über die Grenze des Systems ändern, das heißt: 

t 

Dabei ist Wt die Summe aus der Volumenarbeit und der im System dissipierten Arbeit (z. B. 

Reibungsarbeit). 

Die Energie eines abgeschlossenen Systems bleibt unverändert. Verschiedene Energieformen 

können sich demnach ineinander umwandeln, aber Energie kann weder aus dem 

Nichts erzeugt noch kann sie vernichtet werden. Deshalb ist ein Perpetuum Mobile erster 

Art unmöglich (kein System verrichtet Arbeit ohne Zufuhr einer anderen Energieform 

und/oder ohne Verringerung seiner inneren Energie). 

Eine Einschränkung der Umwandelbarkeit von Wärme in Arbeit ergibt sich erst aus dem 

zweiten Hauptsatz der Thermodynamik. 

2.1.2 2. Hauptsatz: Gesetz des Geschehens 

Der zweite Hauptsatz schränkt die Aussage des ersten Hauptsatzes über die Gleichwertigkeit 

von Wärme und Arbeit ein und ist damit eines der Fundamente der Thermodynamik. Er 

ermöglicht mit der Einführung der thermodynamischen Temperatur und der thermodynamischen 

Entropie als Zustandsgröße die numerische und anschauliche Beschreibung von 

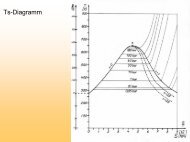
Prozessen z.B. im T-s-Diagramm. 

Er wird im Rahmen der Statistischen Mechanik mit den übrigen Theorien der Physik verknüpft: 

Je nach philosophischem Standpunkt bekommt er eine stochastische Formulierung 

oder wenigstens eine wahrscheinlichkeitsbezogene Begründung. 

Der Zweite Hauptsatz der Thermodynamik in der Formulierung von Clausius lautet: 


dU = δ Q + δW 

Es gibt keine Zustandsänderung, deren einziges Ergebnis die Übertragung von Wärme von 

einem Körper niederer auf einen Körper höherer Temperatur ist. 

Einfacher ausgedrückt: Wärme kann nicht von selbst von einem Körper niedriger Temperatur 

auf einen Körper höherer Temperatur übergehen. Diese Aussage scheint zunächst überflüssig 

zu sein, denn sie entspricht der alltäglichen Erfahrung, wie die über die Anziehungskraft 

der Erde. Dennoch ist sie äquivalent zu allen weiteren, weniger „selbstverständlichen“ 

Aussagen, denn alle Widersprüche zu den anderen Aussagen lassen sich auf einen 

Widerspruch zu dieser zurückführen. 

Der Zweite Hauptsatz der Thermodynamik in der Formulierung von Kelvin und Max 

Planck lautet: 

Es gibt keine Zustandsänderung, deren einzige Ergebnisse das Abkühlen eines Körpers 

und das Heben eines Gewichtes sind. 

Dem ersten Hauptsatz würde die Annahme nicht widersprechen, dass es möglich sei, einer 

- wie immer auch gearteten - Kraftmaschine einen stetigen Wärmestrom zuzuführen, den 

diese vollständig als mechanische oder elektrische Leistung abgibt. Eine solche Maschine 

wird als Perpetuum mobile zweiter Art bezeichnet. Dies wäre z.B. ein mit einer Wärmekraftmaschine 

angetriebenes Schiff, welches steuerbordseitig warmes Seewasser an Bord 

nimmt und dieses um einige Grad abkühlt und dann backbordseitig wieder ins Meer abzulassen. 

Die Abkühlung des geförderten Wassers um ∆T würde den EnergiegewinnQ 

= G ⋅ c ⋅ ∆T 

bereitstellen, die Abkühlung des Weltmeeres wäre unerheblich und der 

erste Hauptsatz würde nicht verletzt. 

Eine entsprechende Formulierung des zweiten Hauptsatzes lautet: 

Auch ein Perpetuum Mobile zweiter Art ist unmöglich.

10 

Eine weitere Aussageform des zweiten Hauptsatzes lautet: 

Es gibt keine Wärmekraftmaschine, die bei gegebenen mittleren Temperaturen der Wärmezufuhr 

und Wärmeabfuhr einen höheren Wirkungsgrad hat als der aus diesen Temperaturen gebildete 

Tkalt 

Carnot-Wirkungsgrad. 

η C = 1− 

Twarm 

Die Nennung der mittleren Temperaturen ist deshalb von Bedeutung, weil in der Regel durch 

Wärmezufuhr oder Wärmeentnahme ein Wärmereservoir seine Temperatur ändert. 

Unmittelbar in diesem Zusammenhang lässt sich weiter formulieren: 

Alle reversiblen Wärme-Kraft-Prozesse mit gleichen mittleren Temperaturen der Wärmezufuhr und 

Wärmeabfuhr haben denselben Wirkungsgrad wie der entsprechende Carnot-Prozess, alle 

irreversiblen Wärme-Kraft-Prozesse haben einen geringeren Wirkungsgrad. 

Mit den in der modernen Thermodynamik festgelegten Begriffsdefinitionen (Wärme, Arbeit, Innere 

Energie, Zustandsgröße, Prozessgröße, adiabatische Zustandsänderung) und mit der systematischen 

Einteilung der Systeme kann über die von Clausius eingeführte Zustandsgröße Entropie S 

eine für alle geschlossenen Systeme allgemein gültige Aussage des zweiten Hauptsatzes in mathematischer 

Form gegeben werden: 

δQ 

δWdiss 

dS = + 

T T 

Dabei ist δWdiss die innerhalb des Systems dissipierte Arbeit (Arbeit, die nicht nach außen gelangt, 

sondern infolge von Reibungs-, Drosselungs- oder Stoßvorgängen die innere Energie erhöht). Sie 

ist immer positiv. Man bezeichnet den entsprechenden Term in der Gleichung als „produzierte Entropie“ 

– im Gegensatz zum ersten Term, der „transportierte Entropie“ genannt wird und auch negativ 

sein kann. Für das adiabate System mit δQ = 0 ergibt sich daraus: 

In einem geschlossenen adiabaten System (dQ=0) kann die Entropie nicht abnehmen, sie nimmt 

in der Regel zu. Nur bei reversiblen Prozessen bleibt sie konstant. 

Q2 Q 

Q 1 

2 T2 

≥ ⇒ ≥ 

T T 

Q T 


2 

η = 

Q 

1 

− Q 

Q 

1 2 

2 = 1− 

≤ 1 

Q1 

Q1 

Der Wirkungsgrad einer Wärmekraftmaschine ist immer kleiner als der Carnot-Wirkungsgrad. 

Der ideale Kreisprozessverlauf ist der Carnet-Prozess, dann gilt das Gleichheitszeichen. Dieser 

wird im Ts-Diagramm durch zwei isotherme und zwei adiabate Verläufe der Zustandsänderung 

des Prozessmediums gebildet. 

Der Begriff "Entropie" entstammt dem Altgriechischen mit der Bedeutung "Verwandlung, 

Transformation, Wendung, Änderung". Der wahrscheinlichste Zustand ist derjenige Makrozustand, 

der die größte Entropie hat, die unter Beachtung der Randbedingungen (z.B. konstante 

Temperatur) möglich ist. Der wahrscheinlichste Makrozustand ist auch der unordentlichste Zustand. 

Daher ist die Entropie auch ein Maß für den Ordnungsgrad eines Zustands: 

„Je unordentlicher ein Zustand, desto größer ist seine Entropie S“. 

Q ist der energetische Wärmeinhalt des Arbeitsmediums und W ist die vom Arbeitsmedium geleistete 

technische Arbeit, U ist die innere thermodynamische Energie des Mediums. Diese 

kann durch Wärmetransport oder durch Arbeitsleistung verändert werden (Druck und Temperaturänderung): 

Die Änderung der inneren Energie in einem abgeschlossenen System kann durch Wärmetransport 

oder durch technische Arbeit erfolgen. Mit der Verwendung von Kleinbuchstaben ist 

der jeweilige spezifische Energieinhalt pro kg des Mediums gemeint. 

Alle spontan ablaufenden Prozesse sind irreversibel. Dort findet immer eine Entropiezunahme 

statt. Beispiele sind die Vermischung von zwei unterschiedlichen Gasen und der Wärmefluss von 

einem heißen zu einem kalten Körper ohne Gewinnung von Arbeit. Die Wiederherstellung des Anfangszustandes 

(„geordneter Systemzustand“) erfordert dann den Einsatz von Energie. 

Reversible Prozesse sind nicht mit einer Erhöhung der Gesamtentropie verbunden und laufen daher 

auch nicht spontan ab. 

1 

T 

− 

T 

∆U 

= ∆Q 

+ ∆W 

= T ⋅ ∆S 

+ S ⋅ ∆T 

1 

1 

2

11 

Mit den Begriffen der Exergie und der Anergie kann der zweite Hauptsatz auch wie folgt formuliert 

werden: 

Die thermische Energie eines Systems besteht aus einem Anteil Exergie und einem Anteil Anergie, 

wobei der exergetische Anteil verschwindet, wenn das System in den Umgebungszustand übergeführt 

wird. 

Die thermische Energie der Wärme besteht aus der Exergie plus der Anergie 

Die Exergie oberhalb der Umgebungstemperatur ist der umwandelbare 

Anteil thermischer Energie in andere Energieformen. 

Wird ein Körper bzw. System mit einem Zustand, der von dem 

der Umgebung abweicht, reversibel in den Umgebungszustand 

gebracht, so wird seine Exergie als Arbeit abgegeben. Die Wärme, 

die ein Körper (z.B. ein heißes Rauchgas im Kessel eines 

Kraftwerks) abgibt, wenn es sich auf Umgebungstemperatur abkühlt, 

kann theoretisch über eine Folge von differenziellen Carnot-Prozessen 

zur Umwandlung in Arbeit genutzt werden. Der 

exergetische Anteil ergibt sich durch Aufsummieren der differenziellen 

Flächenanteile oberhalb der Umgebungstemperatur TU. 


E 

S 

ex = ∫ 

S 

1 

2 

[ T ( S) 

−T 

] ⋅ dS 

U 

Die Wärmesenke für diese Prozesse zur Aufnahme der Anergie Flächenanteil unterhalb TU ist die 

Umgebung. Herrscht bei einem Gas im Ausgangszustand gegenüber dem Umgebungszustand 

nicht nur eine höhere Temperatur, sondern auch ein höherer Druck, so besteht die gesamte Exergie 

nicht nur aus dem exergetischen Anteil der Wärme, sondern zusätzlich aus einem Anteil 

Volumenarbeit. 

Der thermische Wirkungsgrad der realen Wärmekraftmaschine ist also immer kleiner als 1 und – 

bedingt durch die von dem Kreisprozess vorgegebenen Prozessführung und den Eigenschaften 

des Prozessmedium sowie die unvermeidlichen dissipativen Effekte – auch immer kleiner als der 

der idealen Wärmekraftmaschine: 

TU 

Exergie 

η th = 1− 

= 

T thermische Energie 

m, 

zu 

wobei TU die Umgebungstemperatur und Tm,zu die mittlere Temperatur der Wärmezufuhr sind. Tm,zu 

ergibt sich, wenn die gelbe Fläche der Exergie durch ein flächengleiches Rechteck oberhalb der 

Linie der Umgebungstemperatur ersetzt wird. 

Der zweite Hauptsatz hat somit erhebliche technische Auswirkungen. Da viele Maschinen, die mechanische 

Energie liefern, diese über einen Umweg aus thermischer Energie erzeugen (z.B. 

Dampfmaschine: Chemische Energie ⇒ thermische Energie ⇒ mechanische Energie), gelten für 

ihre Wirkungsgrade immer die Beschränkungen des 2. Hauptsatzes. 

Im Vergleich dazu bieten Wasserkraftanlagen, die bei der Umwandlung keine Zwischenstufe über 

thermische Energie benötigen, erheblich höhere Wirkungsgrade, die nur durch technisch bedingte 

Unzulänglichkeiten wie Reibung oder elektrische Verluste verursacht werden und durch Materialauswahl 

oder technisch kluge, reibungsarme Konstruktion mimierbar sind. 

Zusammenfassung der Aussagen des zweiten Hauptsatzes: 

1. Wärme kann nicht von selbst von einem Körper niedriger Temperatur auf einen Körper höherer 

Temperatur übergehen. 

2. Wärme kann nicht vollständig und umso weniger in technischer Arbeit umgewandelt werden, 

je näher die Prozesstemperatur bei der Umgebungstemperatur liegt. Dies wäre die 

Realisierung eines Perpetuum Mobile`s zweiter Art. 

3. Der Wirkungsgrad des Carnot - Prozesses kann nicht übertroffen werden. 

4. Alle spontan (in eine Richtung) ablaufenden Prozesse sind irreversibel. 

5. Alle Prozesse, bei denen Reibung stattfindet, sind irreversibel. 

6. Ausgleichs- und Mischungsvorgänge sind irreversibel. 

7. In einem geschlossenen adiabaten System kann die Entropie nicht geringer werden. 

8. Das Gleichgewicht isolierter thermodynamischer Systeme ist durch ein Maximalprinzip der 

Entropie ausgezeichnet.

Kohle 

Der Carnotprozess im Ts-Diagramm: 

Der Carnot-Prozess ist durch zwei Isotherme T1 und 

T2 und zwei adiabate Zustandsänderungen s1 und s2 

gekennzeichnet. 

2.2 Der technische Dampfkraftwerks - Kreisprozess im Ts- und hs- Diagramm 

2.2.1 Energieumwandlung im Kondensationskraftwerk 

5 

4 

1 

3 

Regler 

6 n,f G 

3~ 

Die adiabate Entspannung von Punkt 1 

nach Punkt 2 setzt die dem hs-Diagramm 

entsprechende Energie in kJ/kg als 

technische Arbeit in der Turbine frei. 

Für die Leistung gilt: 

hs - Diagramm h = f(s): 

Enthalpie h in kJ/kg 

Entropie s in kJ/(kg ⋅ K) 


2 

P = ∆ h ⋅ m 

Fläche 

η = 

Fläche 

P=ω·M 

P 

Kühlwasser 

12 

°C 

500 

400 

300 

200 

100 

0 

T in K 

T1 

Tu=T2 

4 

3 

wt,zu 

4 

qzu 

Exergie 

1 

3 qab 2 

s1 

Flüssikeits 

- wärme 

Anergie 

Verdam- 

pfungs- 

wärme 

s2 

qFl qü 

5 

r 

wt,ab 

s in kJ/(kg·K) 

Ts-Diagramm T=f(s) 

5 

Über- 

hitzungs- 

wärme 

4 

3 

0 2 4 6 8 kJ/kg K 

s 

6 

1 

2 

1 

2

2.2.2 Energieumwandlung im Kraftwärmekopplungsprozess 

Ersatzschaltplan eines KWK Prozesses 

im Heizkraftwerk 


13 

Ts – Diagramm der Wärmeauskopplung 

im KWK - Kreisprozess 

Kraft und Wärme sind elementare Lebensbedürfnisse. Schon seit Jahrmillionen setzt die Natur 

Prinzip der Kraft-Wärme-Kopplung (KWK) ein, also der Nutzung von Brennstoffen zur Erzeugung 

der zum Leben notwendigen Kraft und Wärme in einem einzigen, gekoppelten Prozess. Jede Muskelzelle 

arbeitet nach diesem Prinzip, 

Der Mensch verschafft sich die zum Leben notwendige Kraft und Wärme jedoch nicht nur mit Hilfe 

seiner Körperzellen, sondern durch Techniken, also mit Hilfe des Verstandes. 

Im Laufe der Entwicklung der menschlichen Kultur haben wir zur Befriedigung unserer Bedürfnisse 

nach Kraft, Mobilität und Wärme die verschiedensten Erfindungen gemacht, von der Kleidung und 

dem Feuer über die Nutzung der Körperkraft von Tieren bis zu Segelschiffen, Wind- und Wassermühlen 

sowie schließlich mechanischen Triebwerken. 

Diese Techniken wurden für Kraft und Wärme zunächst getrennt entwickelt: früher waren es 

Ochsengespann und Herdfeuer, heute sind es Automobil, Kraftwerk und Heizkessel. Das war zwar 

thermodynamisch gesehen eine nicht optimale Nutzung der verbrauchten Primärenergie. 

Effizienter ist es, die Wärme auf hohem Temperaturniveau zunächst zur Krafterzeugung zu nutzen 

und dann erst auf niedrigem Temperaturniveau zur Wärmebedarfsdeckung. 

Damit ist aber die Richtung der Prozesse thermodynamisch vorgegeben und entsprechend dem 

zweiten Hauptsatz der Thermodynamik gilt: „Es gibt nichts umsonst“. 

In Kondensationskraftwerken werden nur 30 bis 50% der eingesetzten Primärenergie in Strom 

umgewandelt. 50 bis 70% bleiben als Niedertemperaturwärme ungenutzt und müssen auf niedrigem 

Temperaturniveau, knapp oberhalb der Umgebungstemperatur, über gewaltige Kühltürme an 

die Umgebung abgeführt werden, damit der Dampf bei sehr niedrigem Druck kondensiert und als 

Wasser über die Speisewasserpumpe wieder dem Kessel mit hohem Druck zugeführt werden 

kann. 

KWK-Strom hat in Deutschland derzeit einen Anteil an der gesamten Stromerzeugung von ca. 

11%. Dieser Anteil könnte durch Ausbau der Fernwärmeversorgung erhöht werden sofern die damit 

verbundenen höheren Kosten für die Stromerzeugung dies rechtfertigen. Die Auskopplung der 

Wärme bedeutet allerdings eine Verminderung der verfügbaren Stromerzeugung etwa im Verhältnis 

Wärmeenergie zu Stromenergie von 10:1. Eine kWh Stromeinbuße stellt 10 kWh Wärme bereit. 

In der Papierindustrie, wo produktionstechnisch ganzjährig ein hoher Wärmebedarf besteht, hat 

daher die KWK - Technik bereits seit Anbeginn der Industrialisierung mit der Strom- 

Eigenerzeugung Anwendung gefunden. 

Die höheren Gesamt-Systemkosten bei niedrigen Brennstoffpreisen in den 60 bis 70 er Jahren 

haben dann in der Industrie oft zu einem Ausstieg aus der Strom-Eigenerzeugung geführt. Mit dem 

Anstieg der Stromkosten durch erhöhte Umweltauflagen und staatliche Zusatzlasten wie 

Stromsteuer und EEG/KWK Umlage sowie Offshore - Umlage hat sich in den letzten Jahren ein 

Rückbesinnung auf die KWK-Technik ergeben.

14 

3. Regenerative Energieerzeugung 

3.1 Wasserkraft 

Für die Potentielle Energie des Wassers auf der Höhe h gilt: W = G ⋅ h = m ⋅ g ⋅ h 

dW dm dV 

Für die Leistung gilt: P = = ⋅ g ⋅ h = ⋅ ρ ⋅ g ⋅ h = Q ⋅ ρ ⋅ g ⋅ h 

dt dt dt 

⎡ ⎤ 

⎡ ⎤ 

⎢ 

3 

2 

Q ⎥ m kg m ⎡ h ⎤ ⎢ Q ⎥ ⎡ h ⎤ 

3 kg ⋅ m 

P = ⎢ ⎥ 1000 ⋅ 9, 

81 ⋅ m ⎥ ⋅ ⋅ 9, 

81⋅10 

⋅ 

3 

3 

2 

3 

3 

m s m s 

⎢ ⎢ 

m⎥ 

⋅ = 

m 

⎢m 

⎥ 

⎢ ⎥ 

⎣ ⎦ ⎢ ⎥ ⎣ ⎦ 

s 

⎢⎣ 

s ⎥⎦ 

⎢⎣ 

s ⎥⎦ 

⎡ ⎤ 

⎡ ⎤ 

⎡ ⎤ 

⎢ Q ⎥ 

2 

⎡ h ⎤ 

kg m ⎢ Q ⎥ h 

N m ⎢ Q ⎥ 

3 ⋅ 

⎡ ⎤ 

3 ⋅ 

⎡ h ⎤ 

P = ⎢ ⎥ ⋅ 

⋅ ⋅ ⋅ ≈ ⋅ ⎢ ⎥ ⋅ kW 

m 

⎢m 

⎥ ⋅ 9 , 81⋅ 

10 ⋅ = ⎢ ⎥ ⋅ 

s m 

⎢m 

⎥ 9, 

81 10 10 

3 

2 

3 

3 

s m 

⎢m 

⎥ 

⎢ ⎥ ⎣ ⎦ 

⎢ ⎥ ⎣ ⎦ 

⎢ ⎥ ⎣ ⎦ 

⎢⎣ 

s ⎥⎦ 

⎢⎣ 

s ⎥⎦ 

⎢⎣ 

s ⎥⎦ 

Mit dem Wirkungsgrad η ergibt sich die Leistung in kW, wenn man den Wasserdurchfluss in m 3 /s 

und die Höhe h in m einsetzt zu: P = 10 ⋅Q 

⋅ h ⋅η 

Für ein Wasserkraftwerk ist somit also ein möglichst großer Durchfluss Q und eine möglichst große 

Fallhöhe h zwischen Oberwasserspiegel und Unterwasserspiegel erwünscht. Die Bruttoleistung 

beträgt je m 3 /s Durchfluss und je m Höhendifferenz rd. 10 kW. Die Abbildungen zeigen die wichtigsten 

Bauformen: Francis-Spiralturbine und Laufrad, Kaplan- und Pelton-Turbine. 


P = 10 ⋅Q 

⋅ h 


⋅η 

15 

Je nach verfügbarer Wassermenge und Fallhöhe werden folgende Turbinenarten vorteilhaft 

eingesetzt: 

Francisturbine: 

mittlere Fallhöhen, mittlere Wassermengen. 

Kaplanturbine: 

Geringe Fallhöhen, große 

Wassermengen. 

Peltonturbine: 

Große Fallhöhen, geringe Wassermengen 

Der Anwendungsbereich reicht von 

einer Durchflussmenge 0,5 m 3 /s bis 

1000 m 3 /s und Fallhöhen zwischen 

2 m und 2000 m mit einem 

Leistungsbereich von 30 kW bis 

1000 MW. 

Bei Kleinwasserkraftwerken im 

Leistungsbereich bis 50 kW werden 

Durchströmturbinen (auch unter 

oder oberschlägige Wasserräder) in 

Verbindung mit Asynchrongeneratoren 

und einem Getriebe 

eingesetzt. 

Wasserkraftnutzung ist die älteste 

und günstigste Form der 

elektrischen Energieerzeugung, 

erfordert jedoch entsprechende topologische Gebirgsformationen, die leider nur relativ selten in 

günstiger Form angetroffen werden. 

Die heutigen Turbinen der Wasserkraftwerke verbinden, wie bereits die Wasserräder, meistens 

das Aktions- und Reaktionsprinzip (mit Ausnahme der Pelton- oder Freistrahlturbine). Ihren Namen 

haben sie von dem französischen Ingenieur Claude Burdin, der diesen Begriff erstmals für sein 

1824 entwickeltes Wasserrad verwandte (von lat. "turbo", was soviel wie Kreisel oder Wirbel bedeutet). 

Burdin wollte damit den Preis von 6 000 Francs erringen, der für die Konstruktion eines 

industriell verwertbaren Wasserrads ausgesetzt worden war. 

Den Preis gewann allerdings nicht Burdin, sondern sein Schüler Benoit Fourneyron, der die praktische 

Nutzbarmachung des Reaktionsprinzips mit einer zweiteiligen Konstruktion verwirklichte: Das 

Wasser strömt innerhalb eines geschlossenen Systems zunächst durch die gekrümmten Schaufeln 

eines Leitwerks, bevor es auf die Schaufeln des Laufrads trifft und diese in Bewegung setzt. Fourneyrons 

Maschine hatte den erstaunlich hohen Wirkungsgrad von 80 bis 85 %. Im Prinzip funktionieren 

so bis heute alle "Überdruckturbinen" (Francis-, Kaplanturbinen). Mit dem Unterschied, dass 

Fourneyron das Leitwerk im Innern des Laufrads anbrachte und das Wasser radial abfließen ließ, 

während heute das Leitwerk außen sitzt und das Wasser nach innen durch das Laufrad fließt. 

Francis-Turbinen 

Ein Nachteil von Fourneyrons Reaktions-Turbine war, dass sich beim Übergang des Wassers aus 

dem innen angebrachten Leitwerk in die Schaufeln des Laufrads Turbulenzen ergaben, die bremsende 

Wirkung hatten. 1837 kam der Deutsche Karl Anton Henschel auf die Idee, dies zu vermeiden, 

indem er die Leitschaufeln oberhalb des Laufrads statt in dessen Zentrum anordnete. Weitere 

Verbesserungen ersannen der Amerikaner Samuel B. Howd, der 1838 das Laufrad ins Innere des 

Leitwerks verlegte, sowie der Engländer James Thomson, der verstellbare Leitschaufeln und gekrümmte 

Laufradschaufeln einführte. 1849 konstruierte der anglo-amerikanische Ingenieur James 

B. Francis auf diesen physikalischen Grundlagen eine auch technisch verbesserte Turbine, die 

einen Wirkungsgrad von rund 90 % erreichte. Von ihm hat die Francis-Turbine ihren Namen, die 

heute die verbreiteste und am universelsten verwendbare Turbinenart ist. Die größten Francis- 

Laufräder erreichen ein Gussgewicht von ca. 150 t und Leistungen von über 700 MW. 

Die Francis-Turbine kann auch als Pumpe arbeiten. Dies macht man sich in den Pumpspeicher- 

Kraftwerken zunutze, wo eine Francis-Turbine und der Generator häufig zur sog. Pumpturbine

16 

vereinigt sind, die sich wahlweise auf (stromverbrauchenden) Pumpbetrieb oder (stromerzeugenden) 

Generatorbetrieb umstellen lässt. 

Kaplan-Turbinen 

Speziell für geringe Wasserdrücke entwickelte zu Beginn der zwanziger Jahre der österreichische 

Ingenieur Viktor Kaplan die nach ihm benannte Kaplan-Turbine. Ihr Laufrad gleicht einem Schiffspropeller, 

durch dessen verstellbare Schaufeln die Wassermassen strömen und - umgekehrt wie 

beim Schiffsantrieb - den Propeller antreiben. Das Leitwerk der Kaplan-Turbine lenkt die einströmenden 

Wassermassen so, dass sie parallel zur Welle der Turbine auf die drei bis sechs Schaufeln 

des Laufrads treffen. Sowohl die Laufradschaufeln als auch das Leitwerk sind verstellbar. Dies 

ermöglicht das Anpassen an Schwankungen der Wasserführung und des Gefälles. Große Kaplan- 

Turbinen werden vor allem vertikal eingebaut, so dass das Wasser von oben nach unten durchströmt. 

Die äußerst schnelllaufende Turbine weist in einem weiten Belastungsbereich einen Wirkungsgrad 

von 80 bis 95 % auf. 

Rohr-Turbinen 

Für niedrige Fallhöhen wurde aus der Kaplan-Turbine die Rohr-Turbine entwickelt, die in Laufwasser-Kraftwerken 

Leistungen bis 75 MW erzielt. Die Rohr-Turbinen werden horizontal, in der Richtung 

des strömenden Wassers, eingebaut, so dass Umlenkverluste weitgehend vermieden werden. 

Der Generator befindet sich in Verlängerung der Turbinenwelle in einem vom Wasser umströmten, 

wasserdichten Gehäuse. Rohr-Turbinen sind platzsparend und ermöglichen deshalb 

hervorragend die landschaftliche Einpassung von Wasserkraftwerken. 

Straflo-Turbinen 

Eine Weiterentwicklung der Rohrturbine ist die Straflo-Turbine (von engl. "straight flow"). Generator 

und Turbine bilden hier eine Einheit: Das Laufrad der Turbine trägt auf seinem äußeren Kranz 

zugleich die magnetischen Pole des Rotors, während der Stator, der äußere Teil des Generators, 

in das Turbinengehäuse integriert ist. Das Wasser fließt also durch den Rotor des Generators hindurch. 

Durchström-Turbinen 

Für kleinere Leistungen werden auch sog. Durchström-Turbinen eingesetzt, die sich durch einfachen, 

robusten Aufbau und kostengünstige Konstruktion auszeichnen. Sie verfügen über ein walzenförmiges 

Laufrad mit gekrümmten Schaufeln, denen das Wasser durch einen Leitapparat zugeführt 

wird. Eine solche Turbine mit einer Leistung von 30 kW ist z.B. im Wasserkraftwerk der Familie 

Reiffers in Lünebach (Südeifel) installiert. 

Die Pelton-Turbine 

Aber auch das reine Aktionsprinzip, bei dem nur die Bewegungsenergie des Wassers genutzt wird, 

gelangte zu neuen Ehren: 1880 konstruierte der amerikanische Ingenieur Lester Pelton eine Freistrahlturbine, 

die als Pelton-Turbine bekannt wurde. Sie erinnert vom Aussehen wie vom physikalischen 

Prinzip her am ehesten an das klassische Stoß-Wasserrad. Allerdings gliedert sich jedes 

der bis zu 40 Schaufelblätter in zwei Halbschalen (Becher). Das Wasser wird auch nicht einfach 

über die Schaufeln geleitet, sondern trifft die Mitte der Halbschalen tangential, mit hohem Druck 

aus einer oder mehreren Düsen, so dass der Wasserstrahl in den Schaufelmulden eine Ablenkung 

um fast 180 Grad erfährt und seine Energie fast vollständig an die Turbine abgibt. 

Bei einer Fallhöhe von 1000 Metern schießt der Wasserstrahl mit einer Geschwindigkeit von etwa 

500 km/h aus der Düse. Da die kinetische Energie des Wasserstrahls von der Fallhöhe abhängt, 

ist die Pelton-Turbine typisch für Kraftwerke im Hochgebirge. Die Umfangsgeschwindigkeit des 

Laufrades muss, um das Maximum der Leistung zu erreichen, gleich der halben Austrittsgeschwindigkeit 

des Wasserstrahls sein. Der Wasserstrahl hat dann nach der Umlenkung in der 

Schaufel relativ zum Erdboden den Wert Null, so dass die gesamte kinetische Energie (abzüglich 

der Reibungsverluste) von dem Laufrad aufgenommen wurde. 

v Strahl 

v Strahl 

v = = 2 ⋅π 

⋅ r ⋅ n , n = , = 2 ⋅ g ⋅ h 

Umfang 

2 

4 ⋅π 

⋅ r 

v Strahl 

Die Begrenzung der Durchflussmenge ergibt sich aus der Forderung eines Minimaldruckes p2 an 

der Auslaufstelle im Speicherbecken aus dem Rohrquerschnitt AD an der Einlaufstelle im Speicherbecken 

in Relation zum Querschnitt der Auslassdüse Ad. 

Die für flüssige strömende Medien geltende Bernoulli-Gleichung besagt, dass die Summe aus dynamischem 

Druck, geodätischem Druck (Schweredruck) und statischem Druck konstant ist. Es gilt 

die Bernoulli-Gleichung in Verbindung mit der Kontinuitätsgleichung: 


1 2 


v3 

17 

v1 =0, p1 =1bar =10 

v2 

h1 

D h2 

d β 

u 

5 N/m 2 

Bernoulli-Gleichung: ρ ⋅v + ρ ⋅ g ⋅ h + p = const. 

, Kontinuitätsgleichung: Ad ⋅ v d = AD 

⋅v 

D 

2 

Hierbei sind ρ die Dichte, g die Fallbeschleunigung, h die Höhe und v die Geschwindigkeit des 

Fluids sowie p der statische Druck. Die Bernoulli-Gleichung folgt aus dem Energieerhaltungssatz 

oder aus dem integrierten Impulserhaltungssatz in Verbindung mit der Kontinuitätsgleichung (Massenerhaltungssatz). 

Für die Düsenaustrittsgeschwindigkeit gilt: v d = 2 ⋅ g ⋅ h1 

Für die maximal zulässige Rohreintrittsgeschwindigkeit gilt: 

Wasserspeicher 

2( 

p1 

− p 

2 

2, 

min zul. 

) 

v D = v d + 

− 2 ⋅ g ⋅ h , 2 

2 

ρ 

v v D = , v d = v 3 

Daraus folgt für den minimal zulässigen Einlaufquerschnitt 

v d 

des Fallrohres AD : AD ≥ Ad 

⋅ 

v D 

v 3 

Für die Leistung gilt mit u = für Pmax: 

2 

. 

p3 = 1 bar 

P u 

d d d 

= F ⋅u 

= ρ ⋅ A ⋅v 

⋅( 

v −u) 

⋅( 

1+ 

β) 

⋅u 

3.2 Windkraft 

Elektrische Energieerzeugung durch Umwandlung der kinetischen Energie des Windes in Rotationsenergie 

mittels aerodynamischer Kraftwirkung an den Flügelprofilen in elektrische Energie: 

Ableitung der Leistungsgleichung: 

W = 

1 2 2 

m ( v 1 − v 2 ) 

2 

2 2 ( v v ) 

dW 1 ds 

P = = ρ A 1 − 

dt 2 dt 

Mit der mittleren Windgeschwindigkeit im Wechselwirkungsbereich mit den 

Flügeln: 

ds v1 

+ v 2 

v m = = ergibt sich: 

dt 2 

2 

2 2 ( v v ) 

1 v + v 

P − 

2 2 

1 2 

= ρ A 

Maximum der Leistung: v1 = v, v2/v1 = x ⇒ 

1 2 

3 

f ( P) 

= v ( 1 + x) 

( 1 − x 

[ ( 1 − x ) + ( −2x 

( 1 + ) ] = 0 

df ( P) 

3 

2 

= v 

x 

dx 

v 

1 ⎛ 1 3 ⎞ 

x + 2x 

− 1 = 0 ⇒ x 1, 

2 = − ± ⎜ + ⎟ ⇒ 

3 ⎝ 9 9 ⎠ 

3 2 

1 

3 

v 

2 = folgt für die Leistung: 

2 

) 

16 

27 

df ( P) 

2 

dx 

3 2 

⇒ = v [ 1 − x − 2x 

− 2x 

] = 0 

ρ A v 

2 

Die Leistung eines Windflügelrades ist mit der dritten 

Potenz der Windgeschwindigkeit proportional. Die 

dadurch bedingte stark fluktuierende Leistung muss durch 

Flügelverstellung (pitch-Regelung) oder durch Strömungsabriss 

(stall-Regelung) auf den Nennwert der 

Generatorleistung begrenzt werden. 

P 

= 

A 

1 

3 

x 1 = ⇒ v2 =1/3 v1, mit v 1 = v und 

3 

Leistung in MW 

V1 

20.000 

15.000 

10.000 

5.000 

0 

ds 

V2 

Windleistungseinspeisung vom 09.01. bis 15.01.2009 

Installierte Leistung: 23.312 MW, zeitgleiche 

Summenleistung aller 19.868 Anlagen 

mehrtägige Frostperiode 

in ganz Deutschland 

9.1 11.1 13.1 15.1 

Tage im Januar 2009 (Stunden-Mittelwerte)

18 

800 

h/a 

600 

400 

200 

vm,B vm,K pitch 

stall-Regelung 

v 

% 

100 

75 

50 

25 

0 

0 

0 5 10 15 20 25 m/s 

Windgeschwindigkeit 

3 

3 

ρ A v 

Allgemein gilt: P = cP 

⋅ 

2 

kg 

Dichte der Luft: ρ = 1, 25 , cP ist 

3 

m 

der Leistungsbeiwert: cP = 0,3 bis 0,5 

auch Betz-Faktor genannt. 

-Bereich 

Windenergieanlagen (WEA) werden in 

Leistungsbereichen von 1 bis 6 MW zur 

Stromerzeugung eingesetzt. 

Der Anlauf beginnt bei einer 

Windgeschwindigkeit von 3 bis 4 m/s. Die Nennleistung wird bei rd. 13 m/s Windgeschwindigkeit 

erreicht. Die Abschaltung und Anlagensicherung durch Windfahnenstellung erfolgt bei rd. 25 m/s 

Windgeschwindigkeit. Bei drehbarem Flügel erfolgt die Leistungsregelung durch Verstellung des 

Anstellwinkels (pitch-Regelung), bei starrem Flügel tritt die Leistungsbegrenzung durch Strömungsabriss 

ein (stall-Regelung). 


25.000 

20.000 

15.000 

10.000 

5.000 

0 


Häufigkeit 

1/4 h - Leistungsganglinie der Windleistung in 

Deutschland von So. 1.11. bis Mo. 30.11.2009 

0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 

Zeit in Tage ab dem 1.11. bis 30.11. 2009 

Maximale und minimale Werte der Windleistung 

von 2006 bis 2010 

maximale Leistung 

installierte Leistung 

Für 2011 wird eine EEG geförderte Stromeinspeisung aus Windenergieanlagen von 51.951 GWh 

erwartet. Dafür werden 4,67 Milliarden € an EEG-Vergütung gezahlt, also durchschnittlich 8,99 

ct/kWh. Von den 4,67 Mrd. € sind höchstens 1,0 Mrd. € ersparte Stromerzeugungskosten in den 

ohnehin notwendigerweise vorhandenen Kraftwerken, also rd. 3,6 Mrd. € reine Subvention zu Lasten 

aller Stromverbraucher. Die zeitgleiche Leistungseinspeisung liegt zwischen Null und rd. 90 % 

der installierten Leistung. Daher muss die Summen-Windleistung nahezu mit 100 % der Leistung 

durch die ohnehin notwendigerweise vorhandenen Kraftwerke abgesichert werden. 

Windenergieanlagen können mit höherem Wirkungsgrad betrieben werden, wenn ihre Drehzahl an 

die Windgeschwindigkeit angepasst werden kann. Ihre Drehzahl muss also möglichst variabel veränderbar 

sein. Ein vom Windrad angetriebener Synchrongenerator hat dann eine variable Frequenz 

und kann so nicht direkt mit dem Netz gekoppelt werden. Am besten geschieht daher die 

Netzanbindung über einen Umrichter mit Gleichstromzwischenkreis. Eine weitere Möglichkeit ist 

die Verwendung einer doppelt gespeisten Asynchronmaschine anstatt einer einfachen 

Asynchronmaschine. Diese ist zwar ständerseitig auch direkt mit dem Netz gekoppelt, aber bei ihr 

kann die Drehzahl entsprechend der Windgeschwindigkeit verändert werden. Hierzu wird der Läufer 

über einen Umrichter gespeist, der von der festen Netzfrequenz auf die variable 

(von der Drehzahl abhängigen) Läuferfrequenz übersetzt. Der Umrichter ist in der Regel ebenfalls 

ein Umrichter mit Gleichspannungszwischenkreis. Er 

braucht bei dieser Variante nur für einen Teil 

der Leistung des Windgenerators ausgelegt zu werden, 

während bei der Synchronmaschine die gesamte Leistung 

über den Umrichter übertragen werden muss. 

Bei der 4-poligen Maschine beträgt die synchrone Drehzahl 

(Leerlaufdrehzahl) 1.500 min -1 Drehzahl 1.500 min 

(gelber Arbeitspunkt).Bei 

Unterschreitung dieses Wertes liegt Motorbetrieb 

vor (roter Arbeitspunkt), bei Überschreitung liegt Generatorbetrieb 

vor (grüner Arbeitspunkt). Von der Flügelwelle 

wird die Drehzahl mittels Getriebe etwa 1:30 angehoben. 

-1 

Kippmoment Motorbetrieb 

Motorbetrieb 

Generatorbetrieb 

Kippmoment Generatorbetrieb 


30.000 

25.000 

20.000 

15.000 

10.000 

minimale Leistung 

5.000 

30.592 GWh 39.540 GWh 40.429 GWh 37.772 GWh 36.392 GWh 

0 

1.500 h/a 1.834 h/a 1.734 h/a 1.492 h/a 1.380 h/a 

0 2006 12 2007 24 2008 36 2009 48 2010 60 

Jahr/Monate 

Drehmoment 

Leistung P/Pn

19 

Heylandkreis der Asynchronmaschine auf Basis des vereinfachten Ersatzschaltplanes: 

Beispiel anhand der Maschinendaten der Asynchronmaschine: 

∆400 V, 50 Hz, 5,9 A, 3 kW, cos φ = 0,86, 2890 min -1 . Der Leerlaufstrom beträgt I0 = 1,62 A induktiv. 

Vereinfachter Ersatzschaltplan: 

U 

0 1, 

62 A 

X h = = = = 0, 

94 

I 

I1 

I2´ 

Xk 

, 1 I µ 

A 

I µ 3 3 

400 V 

X 1h 

= = 425, 

5Ω 

0, 

94 A 

` 

I 2 = I1 

− I µ Für Nennbetrieb gilt: I I n I µ − = U Iµ X1h 

` 

2 1 , 

I1n 

= 

I 

° 

n 

5, 

9A 

-j34 

( cosϕ 

− j sinϕ 

) = ( 0, 

86 − j0, 

51) 

= ( 2, 

93 − j1, 

74) 

A = 3,41A 

⋅ e 

3 

3 

` 

I 2 = ( 2, 

93 − j1, 

74) 

− ( − j0, 

94) 

= ( 2, 

93 − j0, 

81) 

A 

` U 

Z 2 = ` 

I 2 

` 

400V 

R2 

= 

= ( 126, 

83 + j35, 

06) 

Ω = + jX k , 

( 2, 

93 − j0, 

81) 

A 

sn 

nn 

2890 

` 

sn 

= 1− 

= 1− 

= 0, 

0367 R 2 = 0, 

0367 ⋅126, 

83Ω 

= 4, 

65Ω 

, X k 

n0 

3000 

Berechnung Ik und I∞: 

= 35, 

06Ω 

⎛ 1 

I 

⎜ k = U 

⎝ jX 1h 

1 

+ ` 

R2 

+ jX k 

⎞ ⎛ 1 1 ⎞ 

⎟ = 400⎜ 

+ 

⎟ = ( 1, 

49 − j12, 

15) 

A = 12,24A ⋅ e 

⎠ ⎝ j425, 

5 4, 

65 + j35, 

06 ⎠ 

U 

I ∞ = I µ + 

jX k 

400 

° 

-j90 

= − j0, 

94 + = − j12, 

35 A = 12,35 A ⋅ e 

j35, 

06 

A 

Maßstäbe für den Heylandkreis: Strommaßstab: m I = 1 

cm 

A kW 

Leistungsmaßstab: 

mP = 3 ⋅U 

⋅ mI 

= 3⋅ 

400V 

⋅1 

= 1, 

2 

cm cm 

mP 

1, 

2 kWs Nm 

Drehmomentenmaßstab: 

mM 

= = 

= 3, 

82 

2 ⋅π 

⋅ n 3000 

0 

cm 

2 ⋅π 

⋅ 

60 

Kippmoment aus dem 

Kreisdiagramm: 

mit mI =1,42 A/cm folgt: 

Mkipp = 4 cm x1,42 x3,82 Nm/cm 

= 21,75 Nm 

Re 


U 

I0 

Pn, Motor 

In 

In,Generator 

Pn, Generator 

Motorbetrieb 

Mn 

Ik 

Mk 

Sn,Motor = 4 % 

s=100 % 

s=75 % 

s=50 % 

s=25 % 

I∞ 

s=0 % 

s=- 25 % 

Generatorbetrieb 

Pk 

P∞ 

R ` 

2 

s 

° 

-j83,02 

Skipp = 18 % 

Bremsbetrieb 

-j 

Sn,Generator = -4 %

20 

3.3 Sonnenenergie 

3.3.1 Photovoltaik 

Bei der Stromerzeugung durch Sonnenstrahlung bei Photovoltaikanlagen wird der Effekt der Ladungsträgerpaarbildung 

durch Strahlungsenergie in einem pn-Übergang eines Halbleiters genutzt. 

Die Strahlungsenergie ES ist gleich dem Produkt aus der Frequenz υ der Strahlung und dem 

Planck`schen Wirkungsquantum h: ES = h ⋅υ 

Der Wirkungsgrad ist abhängig von der Zellenart und liegt zwischen 6 und 18 % bis 23% bei Hybridzellen), 

wobei der untere Wert für amorphe, der mittlere für multikristalline und der obere Wert 

für monokristalline bis hin zu Hybridzellen mit 23 % gilt. 

Wirkungsgrad: 

η = 6 - 7 % für amorphe 

η = 12 -14 % für multikristalline 

η = 17 -18 % für monokristalline 

Siliziumzellen 

10 x 10 cm2 10 x 10 cm 

Leistung 1 W 

2 

10 x 10 cm 

Leistung 1 W 

2 

Leistung 1 W 

Die Zellenspannung von rd. 

0,7 V wird durch Reihenschaltung 

auf die Modulspannung 

von einigen 10 V 

gebracht und dann durch 

weitere Reihen- und Parallelschaltung 

der Module auf 

die Eingangsspannung und 

den Eingangsstrom für die 

Wechselrichter. 

Die Abhängigkeiten von der 

Einstrahlungsleistung und 

von der Temperatur der Zellen 

ist aus den Kennlinenfeldern 

der Photovoltaikzellen 

ersichtlich. 

Für eine effenziente Arbeitsweise 

muss die Zelle 

möglichst kühl gehalten 

werden, dies kollidiert allerdings 

dem höheren Ertrag 

bei voller Einstrahlung. 


R = 0,25 Ω 

R = 1 Ω 

Energie: 

E = h ⋅ ν 

Kathode 

Anode 

Für 2011 wird eine EEG 

geförderte Stromeinspeisung 

aus Photovoltaikanlagen von 19.399 GWh erwartet. Dafür werden 8,02 Milliarden € an EEG- 

Vergütung gezahlt, also durchschnittlich 41,3 ct/kWh. Von den 8,02 Mrd. € sind höchstens 0,4 Mrd. 

€ ersparte Stromerzeugungskosten in den ohnehin notwendigerweise vorhandenen Kraftwerken, 

also rd. 7,6 Mrd. € reine Subvention zu Lasten aller Stromverbraucher. Die Leistungseinspeisung 

der Photovoltaikanlagen ist mit einer Benutzungsdauer der Nennleistung von rd. 800 h noch wesentlich 

mehr fluktuierend, als die Windleistungseinspeisung und steht nachts definitiv nicht zur 

Verfügung, so dass nur Primärenergieverbrauch in den vorhandenen Kraftwerken erspart wird.

3.3.2 Solarthermie 


21 

Die thermisch Nutzung der Sonnenenergie 

zur Stromerzeugung ist wegen der thermodynamischen 

Verluste im Kreisprozess nur 

in sonnenreichen Ländern sinnvoll, da dort 

wegen der hohen Temperaturen die Effizienz 

der Photovoltaikzellen wieder ungünstiger 

wird. Pilotanlagen wurden in 

Spanien in dem Andasol-Projekt gebaut. 

Das erste Parabolrinnen-Kraftwerk Europas, 

Andasol 1 im südspanischen Andalusien 

(Provinz Granada) hat unter dem Projektentwickler 

Solar Millennium AG in Erlangen 

und des DLR am 1. Juli 2009 den 

Testbetrieb aufgenommen und wird nach 

erfolgreichem Abschluss der Testphase den ersten Strom ins spanische Netz einspeisen. Auf einer 

Gesamtfläche von fast zwei Quadratkilometern stehen über 600 Parabolrinnen-Kollektoren, von 

denen jeder einzelne 150 m lang und 5,7 m breit ist. Insgesamt haben die Spiegel eine Fläche von 

über 510.000 m 2 . Bei einer elektrischen Leistung von 50 MW wird eine Jahresarbeit von 179 GWh 

erwartet. 

Das Solarfeld der Andasol-Anlage besteht aus 312 Kollektorreihen mit einer Gesamtlänge von rund 

90 km und rund 210.000 Parabolspiegeln. Die Sonnenstrahlung wird mittels der Parabolspiegel auf 

eine Brennlinie fokussiert und durch entsprechende Erwärmung des Thermoöl- Primärkreislaufs in 

thermische Energie umgewandelt. In der Mitte des 70 Fußballfelder großen Solarfeldes befindet 

sich ein SalzWärmespeicher der als Pendelspeicher aus zwei Tanks von 14 m Höhe und 36 m 

Durchmesser besteht. Das flüssige Salz wird in einem Wärmetauscher durch das mit Sonnenenergie 

erhitzteThermoöl im Primärkreislauf auf bis zu 390° Celsius aufgeheizt. Mit der gespeicherten 

Wärme kann das Kraftwerk dann bis zu 7,5 Stunden nach Sonnenuntergang noch Strom mit voller 

Leistung (50 Megawatt) liefern. Tagsüber wird der Turbinendampf über einen weiteren Wärmtauscher 

erzeugt und der Salzspeicher wieder aufgeladen. Diese thermische Energiespeicher- 

Möglichkeit ist ein wichtiger Vorteil zur planbaren Stromproduktion solarthermischer Kraftwerke 

gegenüber Wind- oder Photovoltaikanlagen. 

Diese höhere Verfügbarkeit erfordert natürlich entsprechende Mehrkosten für die Wärmespeicher 

zur indirekten Stromspeicherung und vermindert die während der Ladezeit verfügbare Leistung. 

Die Benutzungsdauer der Nennleistung beträgt demnach 3.580 h. Die Kosten der Anlage betragen 

310 Mio. € entsprechend 6.200 €/kW. 

Die Einspeisevergütung wurde mit 21 Ct/kWh für 25 Jahre garantiert. 

Die Füssigsalz-Wärmespeicher ermöglichen auch nach Sonnenuntergang noch 7,5 Stunden lang 

eine weitere Stromerzeugung.

22 

3.3.3 Biomasse 

Die Stromerzeugung durch Biomassenutzung erfolgt über einen Gasmotor oder eine Blockkraftanlage 

als Antriebsaggregat für den Generator zur Stromerzeugung. Da diese Art der Stromerzeugung 

auf einen Biomassespeicher basiert, ist sie eben so verlässlich verfügbar, wie die Stromerzeugung 

aus fossilen Primärenergien oder aus Kernenergie. 

Der Nachteil aller vorgenannten Arten der regenerativen Stromerzeugung - mit Ausnahme der 

Wasserkraft - ist, dass diese um ein Vielfaches teurer sind als konventionelle Erzeugungsarten. 

Dazu kommt bei Sonne und Wind die nur dargebotsabhängige Verfügbarkeit. Bei Photovoltaik rd. 

800 h und bei Wind onshore-Anlagen 1.800 h und offshore-Anlagen rd. 3.500 h von den 8.760 

Jahresstunden. Da die Dargebotsabhängigkeit witterungs- bzw. sonnscheinbedingt ist, tritt diese 

großflächig und weitgehend durch die Wetterlage synchronisiert auf, so dass die vorrangig einspeisende 

Summen-Anlagenleistung mit nahezu 100 % durch Ersatzanlagen im standby-Betrieb 

abgesichert sein muss. 

Für 2011 wird eine EEG geförderte Stromeinspeisung aus Biomasseanlagen von 24.315 GWh 

erwartet. Dafür werden 4,25 Milliarden € an EEG-Vergütung gezahlt, also durchschnittlich 17,48 

ct/kWh. Von den 4,25 Mrd. € sind höchstens 1,3 Mrd. € ersparte Stromerzeugungskosten, also rd. 

3,0 Mrd. € reine Subvention zu Lasten aller Stromverbraucher. 

Zusammenfassend wird in 2011 für die prognostizierte Gesamtmenge an EEG Strom, abzüglich 

der direkt vermarkteten Menge von 12.332 GWh von 97.955 GWh erwartet. Dafür erhalten die 

Windanlagenbetreiber für 51.951 GWh eine Vergütung von 4,67 Mrd. €, Die Photovoltaikbetreiber 

für nur 19.399 GWh eine Vergütung von 8,02 Mrd. € und die Biomasse-Anlagenbetreiber für 

24.315 GWh eine Vergütung von 4,25 Mrd. €. 

Nach Abzug der ersparten Stromerzeugungskosten in den ohnehin notwendigerweise vorhandenen 

Kraftwerken verbleibt eine reine Subventionssumme von 14,2 Mrd. € zu Lasten aller Stromverbraucher. 

Das macht bei 40 Millionen Haushalte im Durchschnitt 355 € jährliche Belastung, auf 

welchem Weg auch immer die dort ankommt. Hinzu kommen noch die Aufwandskosten für die 

hierzu notwendigen Netzausbaumaßnahmen. 

Der frühere Umweltminister Trittin sprach im Wahlkampf von einer Belastung durch das EEG- 

Gesetz von nur 1 € pro Monat, und das sei die Sache doch wert! 

In dem Nachfolgenden Diagramm ist die tatsächliche Entwicklung der EEG vergüteten Strommengen 

dargestellt. 

Verdrängte und damit ersparte Stromerzeugzungskosten 

in den 

ohnehin notwendigen Kraftwerken! 


Subvention zu Lasten aller 

Stromverbraucher 

2010 

2011: 14,2 Mrd. € 

Subvention 

Subvention

23 

4. Messung elektrischer Größen 

4,1 Leistungsmessung (Wirkleistung) 

4.1.1 Schaltungen zur Leistungsmessung in unsymmetrische 3 und 4 Leiter Drehstromsysteme 

(Wirkleistungsmessung) 

Dreileitermessung im Vierleitersystem: 

* 

* 

* 

{ U ⋅ I 1 + U ⋅ I 2 + U ⋅ I 3 } = U1 

⋅ I1 

⋅ cosϕ 

1 + U 2 ⋅ I 2 ⋅ cosϕ 

2 + U 3 ⋅ 3 ⋅ cos 3 

P = Re I ϕ 

1 

2 

3 

Falls U 1 = U 2 = U 3 und I 1 = I 2 = I3 

(symmetrisches System) ist P = 3 ⋅ P1 

N 

U1 U2 U3 

3 

U2,3 φ 

I1 

2 

In Dreileitersysteme genügen zwei Leistungsmessgeräte, um in beliebig unsymmetrische Systeme 

die gesamte Leistung zu messen (Aron-Schaltung): 

Wegen I + I + I = 0 gilt: I = − I + I ) 

1 

2 

3 

( 1 3 


2 

{ ( ) } { } { } * 

* 

* 

* 

* 

* 

U ⋅ I − U ⋅ I + I + U ⋅ I = Re ( U − U ) ⋅ I + ( U − U ) ⋅ I = Re U ⋅ I + U 

P = Re ⋅ I 

1 

1 

2 

1 

3 

3 

3 

1 

2 

1 

3 

2 

3 

1, 

2 

1 

U = U 

− j150° 

j 90° 

− j 30° 

− j 90° 

U 1, 

2 = U1, 

2 ⋅ e , U 2, 

3 = U 2, 

3 ⋅ e , U 3, 

1 = U 3, 

1 ⋅ e , U 3, 

2 = U 2, 

3 ⋅ e , 3, 

2 2, 

3 

j ( 180° 

−ϕ 

) 

j ( 60° 

−ϕ 

) 

− j ( 60° 

+ ϕ ) 

I 1 = I1 

⋅ e , I 2 = I 2 ⋅ e , I 3 = I3 

⋅ e , { } * 

P1 Re U 1, 

2 ⋅ I 1 

* 

P2 = Re U 3, 

2 ⋅ I 3 

P 

P 

1 

2 

= 

= 

= , { } 

* 

− j150° 

− j ( 180° 

−ϕ 

) 

j ( 30° 

+ ϕ ) 

{ U 1, 

2 ⋅ I 1} 

= Re{ 

U1, 

2 ⋅ e ⋅ I1 

⋅ e } = Re{ 

U1, 

2 ⋅ I1 

⋅ e } = U1, 

2 ⋅ I ⋅ cos( 

30° 

+ ϕ) 

* 

− j 90° 

j ( 60° 

+ ϕ ) 

− j ( 30° 

−ϕ 

) 

{ U ⋅ I 3 } = Re{ 

U ⋅ e ⋅ I ⋅ e } = Re{ 

U ⋅ I ⋅ e } = U ⋅ I ⋅ cos( 

30° 

− ϕ) 

Re 1 

Re 3, 

2 

3, 

2 

3 

3, 

2 3 

3, 

2 3 

4.1.2 Zweileitermessung im Dreileitersystem: 

L1 

U1,2 

L2 

U2,3 

L3 

L1 

U1,2 

L2 

U2,3 

L3 

P1 

P1 

U3,1 

P2 

P2 

Für symmetrische Last gilt bei rein ohmscher Last ( ϕ = 0) 

: 

1 

P 1 = U1, 

2 ⋅ I1 

⋅ cos( 30° 

+ ϕ ) = U ⋅ I ⋅ ⋅ 3 = P2 

, P = P1 

+ P2 

= U ⋅ I ⋅ 3 

2 

Allgemein gilt für symmetrische Systeme für ( ϕ ≠ 0) 

: 

P = U ⋅ I ⋅ cos 30° 

+ ϕ + cos 30° 

− ϕ 

[ ( ) ( ) ] 

[ cos30° cosϕ 

− sin30° 

sinϕ 

+ cos30° 

cosϕ 

+ sin30° 

sinϕ] 

= U ⋅ ⋅ 3 ⋅ cosϕ 

P = U ⋅ I ⋅ 

I 

Bei digitale Meßsysteme gilt mit 32 Abtastpunkte pro Periodendauer: 

32 

32 

32 

Für die Wirkleistung: 1 

P ⋅ uk 

⋅ i , Blindleistung: 1 

k 

Q = ⋅ ∑u k ⋅ i , Spannung: 

1 

U = ( ) 

k + 8 

∑ uk 

32 

32 

32 

= ∑ 

k = 1 

U3,1 

P3 

I1 

I2 

I3 

I1 

I2 

I3 

Z1 

Z2 

Z3 

Z1 

Z2 

Z3 

Leistung P1 und P2 p.U. 

k = 1 

1 

0,75 

0,5 

0,25 

0 

-0,25 

-0,5 

j 

I2 

U3,1 

U3 

Re 

1 

U1 

U2 

I3 

Leistungsdiagramm ARON-Schaltung 

P1 P2 

U1,2 

1 

3, 

2 

-90 -60 -30 0 30 60 90 

Kapazitive Last 

Phi Induktive Last 

2 

3

24 

4.2 Blindleistungsmessung 

Da Blindleistung eine Leistung ist, die es nicht gibt (Blindleistung ist eine Wirkleistung mit der Besonderheit, 

dass ihr Mittelwert über eine Periode gleich Null ist) kann man diese auch nicht so ohne 

weiteres messen. Was es nicht gibt kann man auch nicht messen! Daher sind einige Voraussetzungen 

und Kniffe erforderlich, um diese besondere Art der Leistung messen zu können. 

Eine Voraussetzung ist das Vorhandensein eines symmetrischen Spannungssystems. Der Spannungspfad 

des Blindleistungsmessgerätes wird an eine Spannung angeschlossen, die zu der 

Spannung des Messobjektes um 90° phasenverschoben ist und vom Betrag her zu dieser Spannung 

in einer festen Relation steht. Daher die Voraussetzung eines symmetrischen Spannungssystems. 

Zu U1 um 90° phasenverschoben ist die Spannung U23 und es 

− j 90° 

gilt: U 23 = 3 ⋅U 

1undU 

23 = 3 ⋅U 

1 ⋅ e 

4.2.1 Dreileiter- Blindleistungsmessung im Vierleitersystem: 

* 

* 

* 

Q = Im U ⋅ I + U ⋅ I + U ⋅ I = U ⋅ I ⋅ sinϕ 

+ U ⋅ I ⋅ sinϕ 


{ 1 

2 

3 } 1 1 1 2 2 2 3 3 3 

1 

2 

3 


, gleiche ϕ (symmetrisches System) ist Qges = 3 ⋅Q1 

Da die Messgeräte aber nur Wirkleistung messen können, werden die drei Phasenspannungen 

durch die jeweils um 90 ° gedrehten Leiterspannungen ersetzt. 

Somit wird gemessen: 

* 

* 

* 

= Re U ⋅ I + U ⋅ I + U ⋅ I 

Q M 

{ } 

2, 

3 1 3, 

1 2 1, 

2 3 

1 ⋅ cos( ϕ1 − 90° 

) + U 3, 

1 ⋅ I 2 ⋅ cos( ϕ 2 − 90° 

) + U1, 

2 ⋅ I 3 ⋅ cos( 3 

QM = U 2 , 3 ⋅ I 

ϕ − 90° 

) 

Da cos 90° = 0 und sin 90° = 1 ist, fallen die ersten Terme der Additionstheoreme weg und es 

bleibt übrig: 

= U ⋅ I ⋅ sinϕ + U ⋅ I ⋅ sinϕ 


Q M 

2, 

3 

1 

1 

3, 

1 


2 

2 

1, 

2 

3 

Das ist aber bis auf den Faktor 3 genau die Gleichung für die Blindleistung des Gesamtsystems. 

D.h. Qges = 

L1 

1 

⋅Q 

M 

3 

= 

1 

⋅ ( U 2, 

3 

3 

Q1 

⋅ I1 

⋅ sinϕ 

1 + U 3, 

1 ⋅ I 2 ⋅ sinϕ 

2 + U1, 

2 ⋅ I 3 ⋅ sinϕ 

) 

I1 

Z1 

Re 

1 

N 

In Dreileitersysteme genügen auch hier zwei Leistungsmessgeräte, um in symmetrische Systeme 

die gesamte Blindleistung zu messen (Aron-Schaltung für Blindleistungsmessung): 

Wegen I + I + I = 0 gilt: I = − I + I ) 

1 2 3 

2 ( 1 3 

{ ( ) } { } { } * 

* 

* 

* 

* 

* 

U 1 ⋅ I 1 − U 2 ⋅ I 1 + I 3 + U 3 ⋅ I 3 = Im ( U 1 − U 2 ) ⋅ I 1 + ( U 3 − U 2 ) ⋅ I 3 = Im U 1, 

2 ⋅ I 1 + U 3, 

2 3 

Q = Im ⋅ I 

3 

U = U 

− j150° 

j 90° 

− j 30° 

− j 90° 

U 1, 

2 = U1, 

2 ⋅ e , U 2, 

3 = U 2, 

3 ⋅ e , U 3, 

1 = U 3, 

1 ⋅ e , U 3, 

2 = U 2, 

3 ⋅ e , 3, 

2 2, 

3 

j ( 180° 

−ϕ 

) 

j ( 60° 

−ϕ 

) 

− j ( 60° 

+ ϕ ) 

I 1 = I1 

⋅ e , I 2 = I 2 ⋅ e , I 3 = I3 

⋅ e , { } * 

Q1 Im U 1, 

2 ⋅ I 1 

* 

Q2 = Im U 3, 

2 ⋅ I 3 

Q 

Q 

1 

2 

= 

= 

U1,2 

L2 

U2,3 

L3 

U1 

U2 

U3 

Q2 

U3,1 

Q3 

= , { } 

* 

− j150° 

− j( 

180° 

−ϕ 

) 

j ( 30° 

+ ϕ ) 

{ U 1, 

2 ⋅ I 1} 

= Im{ 

U1, 

2 ⋅ e ⋅ I1 

⋅ e } = Im{ 

U1, 

2 ⋅ I1 

⋅ e } = U1, 

2 ⋅ I ⋅ sin( 

30° 

+ ϕ) 

* 

− j 90° 

j ( 60° 

+ ϕ ) 

− j( 

30° 

−ϕ 

) 

{ U ⋅ I } = Im{ 

U ⋅ e ⋅ I ⋅ e } = Im{ 

U ⋅ I ⋅ e } = −U 

⋅ I ⋅ sin( 

30° 

− ϕ) 

Im 1 

Im 3, 

2 3 

3, 

2 

3 

3, 

2 3 

3, 

2 3 

I2 

I3 

Da aber nur die Realteilprodukte elektrischer Größen messbar sind, müssen als Messspannung 

die um 90° verdrehten Spannungen, also für U 1, 

2 ⇒ U 3 und für U 3, 

2 ⇒ U 1angeschlossen 

werden. 

Es gilt dann: Q 1 

erforderlich) 

= 3 ⋅Q1, 

M und Q 2 = 3 ⋅Q 

2, 

M , Qges = Q1 

+ Q2 

(Es ist ein Sternpunkt 

Z2 

Z3 

j 

3 

I2 

U2,3 

U3,1 

U3 

φ 

I1 

U1 

U2 

I3 

U1,2 

2

25 

4.2.2 Zweileiter- Blindleistungsmessung im Dreileitersystem: 

* 

* 

* 

Q = Im U ⋅ I + U ⋅ I + U ⋅ I = U ⋅ I ⋅ sinϕ 



{ 1 

2 

3 } 1 1 1 2 2 2 3 3 3 

1 

2 

3 


, gleiche ϕ (symmetrisches System) ist Qges = 3 ⋅Q1 

1 2 3 

2 = ( 1 3 , Für komplexe Größen gilt: { } { } ° − j 90 

Im G = Re G ⋅ e 

{ ( ) } { } { } * 

* 

* 

* 

* 

* 

Im U 1 ⋅ I 1 − U 2 ⋅ I 1 + I 3 + U 3 ⋅ I 3 = Im ( U 1 − U 2 ) ⋅ I 1 + ( U 3 − U 2 ) ⋅ I 3 = Im U 1, 

2 ⋅ I 1 + U 3, 

2 I 3 

Wegen I + I + I = 0 gilt: I − I + I ) 

Q = 

⋅ 


U = U 

− j150° 

j 90° 

− j 30° 

− j 90° 

U 1, 

2 = U1, 

2 ⋅ e , U 2, 

3 = U 2, 

3 ⋅ e , U 3, 

1 = U 3, 

1 ⋅ e , U 3, 

2 = U 2, 

3 ⋅ e , 3, 

2 2, 

3 

j ( 180° 

−ϕ 

) 

j ( 60° 

−ϕ 

) 

− j ( 60° 

+ ϕ ) 

I 1 = I1 

⋅ e , I 2 = I 2 ⋅ e , I 3 = I3 

⋅ e , { } * 

Q1 Im U 1, 

2 ⋅ I 1 

* 

Q2 = Im U 3, 

2 ⋅ I 3 

Q 

Q 

1 

2 

= 

= 

= , { } 

* 

− j150° 

− j( 

180° 

−ϕ 

) 

j ( 30° 

+ ϕ ) 

{ U 1, 

2 ⋅ I 1} 

= Im{ 

U1, 

2 ⋅ e ⋅ I1 

⋅ e } = Im{ 

U1, 

2 ⋅ I1 

⋅ e } = U1, 

2 ⋅ I ⋅ sin( 

30° 

+ ϕ) 

* 

− j 90° 

j ( 60° 

+ ϕ ) 

− j( 

30° 

−ϕ 

) 

{ U ⋅ I } = Im{ 

U ⋅ e ⋅ I ⋅ e } = Im{ 

U ⋅ I ⋅ e } = −U 

⋅ I ⋅ sin( 

30° 

− ϕ) 

Im 1 

Im 3, 

2 3 

3, 

2 

3 

3, 

2 3 

3, 

2 3 

Da die Messgeräte aber nur Realteilprodukte elektrischer Größen bilden können, also nur Wirkleistung 

messen können, werden die beiden Leiterspannungen durch die jeweils um 90 ° gedrehten 

Leiterspannungen ersetzt. An den Spannungsspulen wird für U 1, 

2 ⇒ U 3 , (denn 

− j 90° 

U 1, 

2 ⋅ e = −U 

3 ⋅ 3 ) und für U 3, 

2 

− j 90° 

⇒ U 1, 

(denn U 3, 

2 ⋅ e = U 1 ⋅ 3 ) angeschlossen. Es gilt 

dann: Q 1 = 3 ⋅Q1, 

M und Q 2 = − 3 ⋅Q 

2, 

M , Qges = Q1 

+ Q2 

Da im Dreileitersystem kein Sternpunkt 

vorhanden ist, muss ein solcher über drei gleich große Widerstände R als künstlicher Sternpunkt 

gebildet werden. 

Q 

Q 

1, 

M 

2, 

M 

= 

= 

− j 60° 

− j ( 180° 

−ϕ 

) 

− j (´ 60° 

−ϕ 

) 

{ − U 3 ⋅ e ⋅ I1 

⋅ e } = Re{ 

U 3 ⋅ I1 

⋅ e } = U 3 ⋅ I ⋅ cos( 

60° 

− ϕ) 

j180° 

j ( 60° 

+ ϕ ) 

j (´ 240° 

+ ϕ ) 

{ U ⋅ e ⋅ I ⋅ e } = Re{ 

U ⋅ I ⋅ e } = U ⋅ I ⋅ cos( 

240° 

+ ϕ) 

Re 1 

Re 1 

3 

1 3 

1 3 

Mit cos ( 60° 

− ϕ ) = sin( 

30° 

+ ϕ) 

, ( 240° 

+ ϕ) = − sin( 

30° 

− ϕ) 

U ⋅ I ⋅ ( 30° 

+ ) = Q ⋅ 3 

−U 

cos folgt: 

Q1 = 1, 

2 1 sin ϕ 1, 

M , Q2 = 3, 

2 ⋅ I3 

⋅ sin ( 30° 

− ϕ ) = −Q2, 

M ⋅ 3 , 

Qges . = Q1 

+ Q 2 

Re 

1 

L1 

U1,2 

Leistung P, P1 und P2 

p.U. 

L2 

U2,3 

L3 

2 

1,5 

1 

0,5 

0 

-0,5 

Q1 

R U3 U1 

U3,1 

Q2 

Wirkleistungsdiagramm ARON-Schaltung 

P1 P2 P gesamt 

-90 -60 -30 0 30 60 90 

Kapazitive Last Phi Induktive Last 

I1 

I2 

I3 

Z1 

Z2 

Z3 

2 

Leistung Q, Q1 und Q2 

p.U. 

1 

0 

-1 

-2 

j 

3 

I2 

U2,3 

U3,1 

U3 

φ 

I1 

U1 

U2 

Blindleistungsdiagramm ARON-Schaltung 

Q1 Q2 Q gesamt 

I3 

U1,2 

-90 -60 -30 0 30 60 90 

Kapazitive Last 

Phi Induktive Last 

2

26 

4.3 Komplexe Leistung 

Wirk- und Blindleistung als Komponenten der komplexen Leistung 

~ 

u 

u 

I 

U 

) 

Z 


j 

U) 

ε 

) 

u 

2 

U 

φ 

δ 

ωt 

j⋅( 

ωt 

+ ε ) − j⋅( 

ωt 

+ ε ) 

() t = u ⋅ cos( 

ωt 

+ ε ) = e + e 

1 

jωt 

* − jωt 

() t = ⋅ [ U ⋅ e + U ⋅ e ] 

i 

i 

p 

2 

) 

= i ⋅cos 

ωt 

+ δ 

) 

i 

2 

j⋅( 

ωt 

+ δ ) − j⋅( 

ωt 

+ δ ) 

() t ( ) = e + e 

1 jωt 

* − jωt 

() t = ⋅ [ I ⋅e 

+ I ⋅ e ] 

2 

1 * * 1 

j 2ωt 

* * − j 2ωt 

() t = [ U ⋅I 

+ I ⋅U 

] + [ U ⋅I 

⋅e 

+ U ⋅I 

⋅e 

] 

p 

2 

2 

Der Mittelwert der Leistung ist gleich dem Integralwert 

über eine Periode von 0 bis ωt = 2π. 

Der erste Term ist gleich dem Argument des Terms selbst, 

der zweite Term ergibt den Integralwert Null. 

T 

1 

P = p 

T ∫ 

0 

1 * * 

() t ⋅dt 

= ( U ⋅I 

+ I ⋅U 

) 

2 

jε 

jδ 

U = U ⋅e 

, I = I ⋅e 

, ϕ = ε − δ 

ϕ > 0 der Strom eilt der Spannung nach 

(induktive Last). (Merkregel: I nach dem 

I 

ϕ < 0 der Strom eilt der Spannung vor 

Re (kapazitive Last) 

ϕ = 0 Strom und Spannung Phasengleich 

(ohmsche Last) 

1 jωt 

j⋅ε 

− jωt 

− j⋅ε 

[ ] = ⋅ U[ 

e ⋅ e + e ÷ e ] 

2 

1 jωt 

j⋅δ 

− jωt 

− j⋅δ 

[ ] = ⋅U[ 

e ⋅ e + e ÷ e ] 

1 j 2ωt 

* * 

* * − j 2ωt 

() t = u() 

t ⋅ i() 

t = [ U ⋅I 

⋅e 

+ U ⋅I 

+ I ⋅U 

+ U ⋅I 

⋅e 

] 

2 

Diesen Wert der Leistung nennt man Wirkleistung, da der Mittelwert über eine Periode ungleich 

Null ist, wenn U > 0 und I > 0 sind. Dieser Mittelwert ist gleich der Hälfte der Summe aus dem Produkte 

aus der konjugiert komplexen Spannung mal dem komplexen Stromwert und dem konjugiert 

komplexen Strom mal dem komplexen Spannungswert. Es ist für die Wirkleistung daher auch zulässig 

und richtig, eines der beiden Produktwerte zu ermitteln ohne diesen Wert dann zu halbieren. 

Diese Beliebigkeit hat allerdings eine Auswirkung auf das Vorzeichen der Blindleistung, die man 

als den imaginären Anteil der komplexen Leistung definiert. 

* 

Man definiert daher die Scheinleistung zu: S = P + jQ = U ⋅I 

oder 

* 

U ⋅I 

* 

Wir wählen die Form: S = P + jQ = U ⋅I 

, weil dann die induktive 

Blindleistung als positive Blindleistung in der komplexen 

Leistungsebene erscheint. 

Hier wird auch deutlich, dass im physikalischen Sinne die Leistung 

nur als Wirkleistung existiert, die Blindleistung ist eine Wirkleistung 

mit der Eigenschaft, dass sie über eine Periode gemittelt 

den Wert Null ergibt. 

In oberschwingungsbehafteten Netzen ist nur die Grundschwingung 

des Stromes Träger der Wirkleistung. 

Blindleistung 

2 

j 

U 

Scheinleistung 

U I* 

I 

Q 

Re 

P 

U * I 

I * 

Wirkleistung 

U *

27 

4.4 Leistungsanpassung bei Wechselstrom und komplexen Widerständen 

Aus der Gleichstromtechnik ist bekannt, dass die maximale Leistung von einer Quelle an den 

Abschlusswiderstand abgegeben wird, wenn Ra =Ri ist (Leistungsanpassung). 

= 

U0 

Ri 

P 

I 

Ua 

Nach der Spannungsteilerregel ist: 0 U 

Z a 

U a = ⋅ 

Z + Z 

U 

Z 

= ⋅U 

, 

a 

Mit: a 

0 

Z i + Z a 

Ra 

U 

2 

a 

~ 

i 

U0 

2 

a 

2 

Z a 

Im Ersatzschaltplan der Kompensation durch Reihenresonanz ergänzen sich die Blindwiderstände 

zu Null und im Ersatzschaltplan durch Parallelresonanz zu unendlich, so dass diese im jeweiligen 

Ersatzschaltplan entfallen und nur noch die Wirkwiderstände Ri und Ra erscheinen. 


Zi 

a 

P 

Z 

2 

= ⋅U 

0 folgt: 

Z + 

⎪ 

⎧ 

2 

Z a U ⎪ 

⎫ 

⎪ 

⎧ 2 

U ⎪ 

⎫ 

2 

⋅ 0 

0 

U0 

Pa = Re ⎨ ⎬ = Re⎨ 

⋅ Z a ⎬ = ⋅R 

2 

2 

2 

⎪⎩ Z i + Z a ⎪⎭ ⎪⎩ Z i + Z a ⎪⎭ Z i + Z a 

U 

P ⋅R 

2 

0 

a = 2 

2 

( Ri 

+ Ra 

) + ( X i + X a ) 

a 

i 

I 

Ua Za 

{{ } * 

U I 

Pa = Re a ⋅ a 

P a 

⎪⎧ 

U 

Re⎨{ 

U a ⋅ 

⎪⎩ Z 

2 

⎪⎧ 

U ⎪⎫ 

a 

P a = Re⎨ 

* ⎬ 

⎪⎩ Z a ⎪⎭ 

* 

a 

= * 

a 

⎪ 

⎧ 2 2 

Z ⎪ 

⎫ 

a ⋅U 

0 

P a = Re⎨ 

2 * ⎬ 

⎪⎩ Z i + Z a ⋅ Z a ⎪⎭ 

Notwendige Bedingung für den relativen Extremwert von Pa ist, dass die partiellen Ableitungen 

nach Ra und Xa gleich Null sind: 

δP 

a 

δR 

a 

δP 

δX 

a 

a 

= U 

= U 

2 

0 

⋅ 

δP 

a 

δR 

a 

δPa 

= 0 und = 0 

δX 

( Ri 

2 

+ Ra 

) + ( X i 

2 

+ xa 

) − 2 ⋅ ( Ri 

+ Ra 

) 

( R + R 

2 ) + ( X + x 

2 ) 

2 

[ i a 

i a ] 

a 

⋅ R 

a 

a 

= 0 

( ) ( ) ( ) 2 

2 

⋅ R i + Ra 

⋅ Ra 

= Ri 

+ Ra 

+ X i + x 

( ) 2 

R i 

2 2 

2 

⋅ Ra 

+ 2 ⋅ Ra 

= Ri 

+ 2 ⋅ Ri 

⋅ Ra 

+ Ra 

+ X i + x 

( ) 2 

2 2 

R a = Ri 

+ X i + xa 

− 2 ⋅ ( X i + X a ) ⋅R 

a 

= 0 ⇒ X 

2 

2 2 

a 

( R + R ) + ( X + x ) 

−X 

i 

2 a 

2 ⋅ 

a 

2 

0 

⋅ 

[ i a 

i a ] 

= ⇒ R a = Ri 

⇒ Z a = Z 

Das Leistungsmaximum wird erreicht, wenn Ra = Ri ist und der innere Blindwiderstand durch den 

äußeren Blindwiderstand kompensiert wird. 

Beispiel Ersatzspannungs-und Ersatzstromquelle: 

Kompensation durch Reihenresonanz: Kompensation durch Parallelresonanz: 

I 

I 

Ri 

Xi 

~ U0 Zi Ua 

Pmax 

Ra 

Xa=-Xi 

Za = Zi * 

~ 

Ik 

Zi 

Ua 

* 

i 

⎪⎫ 

⎬ 

⎪⎭ 

Ri Xi Ra 

Xa=-Xi 

Pmax 

Za = Zi *

Funktionswert 

1,00 

0,75 

0,50 

0,25 

0,00 

-0,25 

-0,50 

-0,75 

-1,00 

28 

4.5 Nachweis für die Behauptung, dass nur die Grundschwingung des Stromes bei 

sinusförmiger Spannung Träger der Wirkleistung ist. 

Die Spannung sei rein sinusförmig gegeben als cosinus-Funktion der Zeit mit der Kreisfre- 

uˆ 

jωt 

− jωt 

uˆ 

quenz ω: u() 

t = cosωt = ⋅ ( e + e ) = ⋅ ( cosωt 

+ j sinωt 

+ cosωt 

− j sinωt 

) 

2 

2 

Der Strom sei gegeben als eine Summe aus der Grundschwingung mit der Kreísfrequenz ω 

und den Oberschwingungen υ ⋅ ω wobei υ = 3 , 5, 

7,..., 

2n 

+ 1ist. 

Die gradzahligen Oberschwingungen entfallen gemäß den Gesetzen der Fourier-Analyse bei 

in t = T/2 bzwω t = π , spiegelsymmetrischer Kurvenform des Wechselstromes. 

Damit gilt für den oberschwingungsbehafteten Strom: 

2n+ 

1 

n 

iˆ 

2 + 1iˆ 

υ υ jυ⋅ωt 

− jυ⋅ωt 

i() 

t = ∑ cos( 

υ ⋅ωt 

) = ∑ ⋅ ( e + e ) 

υ = 1 2 

υ = 1 2 

Die Leistung ergibt sich aus dem Produkt aus Spannung mal Strom: 

n+ 

u jωt 

− jωt 

iυ 

jυ⋅ωt 

− jυ⋅ωt 

p() 

t = u() 

t ⋅ i() 

t = ⋅ ( e + e ) ⋅ ∑ ⋅ ( e + e ) 

υ = 

1 2 

ˆ 

ˆ 

2 

1 2 

2n+ 

1ˆ 

2n+ 

1 

i 

ˆ 

υ uˆ 

jωt 

− jωt 

jυ⋅ωt 

− jυ⋅ωt 

iυ 

uˆ 

jωt 

( 1+ 

υ ) j ( 1−υ 

) − jωt 

( 1−υ 

) − j ( 1+ 

υ ) 

p () t = ∑ ⋅ ⋅ ( e + e )( e + e ) = ∑ ⋅ ⋅ ( e + e + e + e ) 

υ= 

1 2 2 

υ = 1 2 2 

û 

iˆ 

υ 

Mit U = und I υ = folgt: 

2 

2 

2n+ 

1 

2n+ 

1 

1 

ω υ 

υ ω υ 

υ 

() = ⋅ ∑ ˆ j t( 

1+ 

) j ( 1− 

) − j t ( 1− 

) − j ( 1+ 

) 1 

p t U Iυ 

⋅ ( e + e + e + e ) = ⋅U 

∑Iˆ 

υ ⋅ 2 cosωt 

( 1+ 

υ) 

+ cosωt 

( 1−υ 

) 

2 

2 

p 

υ= 

1 

= ∑ υ 

υ 

+ 2n 

1 

U Iˆ 

= 1 

() t [ cosωt 

( 1+ 

υ) 

+ cosωt 

( 1−υ 

) ] 


υ = 1 

[ ] 

Für den Mittelwert der Leistung über eine Periode ergibt sich als „Wirkleistung“: 

T 

ωT 

2π 

2n+ 

1 

1 

1 

1 

P = ∫ p() 

t ⋅dt 

= ∫ p( 

ωt 

) ⋅ d( 

ωt 

) = ∫U ∑Iˆ 

υ cosωt 

( 1+ 

υ) 

+ cosωt 

( 1−υ 

) ⋅ d ωt 

T ωT 

2π 

P 

0 

1 2π 

2π 

0 

2n 

1 

= ∫ ∑ + 

U 

2π 

0 

Iˆ 

υ 

υ = 1 

0 

0 

υ = 1 

[ cosωt 

( 1+ 

υ) 

+ cosωt 

( 1−υ 

) ] ⋅ d( 

ωt 

) = 0 

1 

1 

P = U ⋅Iˆ 

1 

⋅ 

2 ∫ π 

π 

2π 

[ ] ( ) 

für υ ≠ 1 

[ cos2ωt 

+ 1] 

⋅ d( 

ωt 

) = U ⋅I1 

⋅ ( 2 − 0) 

= U I1 

, Ergebnis: 1 I U P ⋅ = 

Beispiel eines reinen Oberschwingungsstromes: = i ( sin 3ω 

t + sin5ω 

t + sin7ω 

t + sin11ω 

t ) 

Λ 

Wechselstrom, -Spannung und -Leistung 

Spannung Strom 3. Oberschwingung Leistung 

0 30 60 90 120 150 180 210 240 270 300 330 360 

Argument 

1,00 

0,75 

0,50 

0,25 

0,00 

-0,25 

-0,50 

-0,75 

-1,00 

Der Mittelwert der Leistung 

ist gleich Null. 

Aber es ist wohl eine 

Blindleistung als 

Verzerrungsleistung 

vorhanden. 

Funktionswert 



0 30 60 90 120 150 180 210 240 270 300 330 360 

Argument 

Funktionswert 

1,00 

0,75 

0,50 

0,25 

-0,75 

-1,00 

Funktionswert 

i ges 

1,00 

0,75 

0,50 

0,25 

0,00 

-0,25 

-0,50 

-0,75 

-1,00 


Spannung Strom 3.+5.+7.+11.Oberschwingung Leistung 



0 30 60 90 120 150 180 210 240 270 300 330 360 

Argument 

0,00 

0 

-0,25 

-0,50 

30 60 90 120 150 180 210 240 270 300 330 360 

Argument 

Funktionswert 

1,00 

0,75 

0,50 

0,25 

-0,75 

-1,00 



0,00 

0 

-0,25 

-0,50 

30 60 90 120 150 180 210 240 270 300 330 360 

Argument 

Man erkennt die Spiegelsymmetrie 

des Stromes da gilt: 

⎛ T ⎞ 

i () t = −i⎜ 

t − ⎟ 

⎝ 2 ⎠ 

Die Oberschwingungen löschen 

sich teilweise gegenseitig aus.

29 

5. Netzregelung 

5.1 Primärregelung mit statischer Frequenz-Leistungs-Kennlinie 

5.1.1 Drehmoment und Leistung von Strömungsmaschinen 

Das Drehmoment durch die Kraftwirkung des strömenden Mediums auf die Turbinenschaufeln ist 

maximal bei Stillstand des Rotors bei ω = 0 . Es ist gleich Null, wenn die Umfangsgeschwindigkeit 

gleich der Strömungsgeschwindigkeit des ausströmenden Mediums ist, da dann keine Kraft mehr 

auf die Turbinenschaufeln ausgeübt wird: ω = ωmax 

. Wird für 0 ≤ ω ≤ ωmax 

ein linearer Zusammhang 

angenommen, so gilt: 

⎛ ω ⎞ 

M = M ⋅ 

⎜ − 

⎟ 

max 1 Für die Leistung gilt: P = ω ⋅ M 

⎝ ωmax 

⎠ 

⎛ ω ⎞ 

P = M ⋅ ⋅ 

⎜ − 

⎟ 

max ω 1 Dies ist eine quadratische 

⎝ ωmax 

⎠ 

Abhängigkeit von der Winkelgeschwindigkeitω . 

Die maximale Leistung ergibt sich durch Differentiation 

und Null setzen zu: 

dP ⎡⎛ 

ω ⎞ ⎛ 1 ⎞⎤ 

= M ⎢ ⎜ 

⎟ + 

⎜ 

⎜− 

⋅ 

⎟ 

max ⋅ 1− 

ω ⎥ 

dω 

⎣⎝ 

ωmax 

⎠ ⎝ ωmax 

⎠⎦ 

⎛ ω ⎞ 

= max ⋅ 

⎜ 

⎜1− 

2 

⎟ = 0 

ω ⎝ ωmax 

⎠ 

M 

Drehmoment- / Leistungsdiagramm 

M P 

2 

Werte normiert 

1,5 

auf Mn und Pn 

1 

0,5 

0 

0 0,5 1 1,5 2 

dP 

d 

∆P 

1 Pn 

Leistungskoeffizient 

K = = ⋅ 

1 ∆f 

s fn 

Daraus folgt: ω = ωn 

= ωmax 

2 

Strömungsmaschinen werden mit einer Drehzahl betrieben, die der Hälfte der maximal erreichbaren 

Geschwindigkeit im Leerlauf entspricht. (Durchgangsdrehzahl). 

5.1.2 Primärregelung der Kraftwerke durch statische Regelkennlinie: 

∆f 

f tanα 

= ≈ s 

Ys 

∆P 

3 

R 

Italien- Blackout am 

α 

28. September 2003 

fn 

n 

T 

G 

∆f 

fn 

∆f 

⋅ P 

3~ 

n 

Statik s = = 

∆P 

P ∆P 

⋅ f 

PÜ 

0 

0 

Üblicher Wert s = 4 % 

Pn 

5.1.3 Sekundärregelung mit dem Netzkennlinienverfahren nach Graner 

Durch die Sekundärregelung werden die Übergabeleistungen an den Übergabestellen zu den 

Nachbarnetzen und die Frequenz wieder auf ihre jeweiligen Sollwerte zurückgeführt. 

Sekundärregelung im Verbundbetrieb der Kraftwerke zweier Netzgebiete 

G 

3~ 

PG1 

Es sei in der Ausgangslage: PG1 =PN1 und PG2 = PN2, dann ist die Übergabeleistung Pü =0 und die 

Frequenz ist gleich der Nennfrequenz f = 50 Hz. Der Arbeitspunkt liegt im Schnittpunkt der beiden 


n 

PN1 

N1 

n 

K 

P 

Übergabeleistung Pü 

Drehmoment M, Leistung P 

Zunahme der Leistung im 

Netzgebiet N2 um ∆PN2 mit der 

Folge, dass Pü um ∆P1 ansteigt 

N2 

PN2+∆PN2 

G 

3~ 

PG2

P2 

30 

Netzkennlinien (Frequenz-Leistungskennlinien K1 und K2). Die Kraftwerke im Netzgebiet N1 liefern 

die Leistung PG1 und die Kraftwerke im Netzgebiet N2 liefern die Leistung PG2. 

f 

f 

Leistungskoeffizient 

∆P 

1 Pn 

K = = ⋅ 

∆f 

s f 

K2 ´ 

f 

fn 

f ´ 

Nun soll die Last im Netzgebiet N2 um ∆PN2 zunehmen. Die Folge ist eine Frequenzabsenkung 

durch die Lastzunahme im Netz 2. Diese beträgt: 

Infolge der Frequenzabsenkung steigt die Last der Kraftwerke im Netzgebiet N1 um 

P = K ⋅ ∆f 

P = K ⋅ ∆ an. 

∆ 1 1 und im Netzgebiet 2 um ∆ 2 2 f 

Nun greift die Sekundärregelung ein und bildet die Stellgrößen: 

YS1 = K1∆f 

+ ∆Pü 

und YS2 = K 2∆f 

+ ∆Pü 

. = K ∆f 

− K ∆f 

= 0 Y = K ∆f 

+ K ∆f 

= K ⋅ ∆f 

= ∆P 

YS 1 1 1 , S2 

2 1 

N 2 

Im Netzgebiet N2 wird die Frequenz-Leistungskennlinie durch Aktivierung von Leistung parallel 

nach oben verschoben, so dass sich der ursprüngliche Arbeitspunkt A wieder einstellt. 

5.1.4 Tertiärregelung zum Zeitausgleich zwischen 

astronomischer Zeit tA und der Synchronzeit 

tS: 

TA 

1 

tS = ⋅ f t ⋅ dt A für f = const ∆t 

S 

f ∫ ( ) , 

. : 

n 0 


50,3 

50,2 

50,1 

50 

49,9 

Frequenz Hz 

Blackout in Italien am 28.9.2003 um 3.29 Uhr 

Erzeugerleistung > 

Verbraucherleistung 

49,8 

0:00 1:00 2:00 3:00 4:00 5:00 6:00 

Zeit 

Auf der Zeitachse lösen die einzelnen Regelverfahren 

einander ab: Die Primärregelung ist in den ersten 30 Sekunden wirksam, dann folgt die Sekundärregelung 

in dem verursachenden Netzgebiet, um in den folgenden 15 Minuten den Normalzustand 

bezüglich der Frequenz und Leistungen zu den benachbarten Netzen in allen Netzgebieten wieder 

herzustellen. Nach Absprache kommt dann ggfs. die Minutenreserveleistung dort zum Einsatz, wo 

keine ausreichende Regelleistung mehr verfügbar ist, mit entsprechender Anpassung der Sollwerte 

für die Übergabeleistungen. 

Primär- 

Regelung 

50,05 

Hz 

50,1 

50 

49,95 

PG1 ´´ 

K1 

A2 

∆P2 

´ PG1 PG2 

PG2 

Sekundär- 

Regelung 

A 

∆PN2 

∆P1 

= 

Minutenreserve - Leistung 

30 s 15 min 1 h 

Frequenzverlauf UCTE Netz Europa 

02.09.2010 

f 

f 

n 

A1 

K2 

PG1 ´ 

PG2 ´´ 

⋅ ∆t 

49,9 

00:00:00 06:00:00 12:00:00 

Zeit 

18:00:00 00:00:00 

A 

50,05 

Hz 

50,1 

50 

49,95 

49,9 

n 

∆f 

∆PN2 

Frequenzverlauf UCTE Netz Europa 

t 

fn 

02.09.2010 

P1 

06:00:00 07:00:00 08:00:00 09:00:00 

Zeit

31 

6. Ausgewählte Themen der Netzpraxis 

6.1 Verschiebungs- und Verzerrungsblindleistung 

Wechselstromleistung nicht sinusförmiger Ströme nach DIN 40110: 

2 2 2 

2 2 

Scheinleistung 

1 2 3 ... ... n I I I I I U I U S + + + + + ⋅ = ⋅ = υ 

Für spiegelsymmetrische Funktionen d.h. i( t ) = −i( 

t −T 

) entfallen die geradzahligen 

2 

2 2 2 

2 2 

Oberschwingungen, so dass gilt: 

1 3 5 ... ... n I I I I I U I U S + + + + + ⋅ = ⋅ = ν 

Träger der Wirkleistung ist nur die Grundschwingung des Stromes in Verbindung mit der 

sinusförmigen Spannung: 

P = P = U ⋅I 

⋅cosϕ 

Für die Blindleistung Q gilt: 


1 

2 

Q = S − P 

Die Blindleistung Q setzt sich zusammen aus der Grundschwingungsblindleistung Q1 und der 

Verzerrungsleistung D: 

Q = U ⋅I 

⋅ sinϕ 

1 

1 

1 

2 

D + 

1 

2 2 

2 2 

= U ⋅ I3 

+ I5 

+ ... + Iυ 

... In 

Für die Grundschwingungs-Scheinleistung S1 gilt: 

S1 = U ⋅I1 

Für den Leistungsfaktor λ als das Verhältnis von Wirkleistung zu Scheinleistung gilt: 

λ = = i ⋅ cosϕ1 

g 

P 

I1 

mit g i = 

S 

I 

gi ist der Grundschwingungsgehalt des Stromes. 

cosφ1 ist der Grundschwingungs-Leistungsfaktor (auch Verschiebungsfaktor genannt). 

Für nichtsinusförmige Ströme gilt: λ < cosϕ1 

Für die Scheinleistung S gilt: 

S + 

2 2 2 2 

= P + Q1 

D , 

2 2 

S = P + Q1 

+ 

Die Verzerrungsblindleistung lässt sich auch mit dem Klirrfaktor k und der Scheinleistung S 

ausdrücken: 

D = S ⋅ k 

In der Nachrichtentechnik werden nichtlineare Verzerrungen durch das Dämpfungsmaß Dk 

(Klirrdämpfung) in dB oder als Klirrfaktor k in Prozent angegeben. Auch der englische Ausdruck 

THD = Total Harmonic Distortion ist für die Verzerrungsgröße Klirrdämpfung üblich. Das 

Dämpfungs-maß Dk ist der Pegelunterschied zwischen Klirranteil (unerwünschte 

Oberschwigungen) und dem gesamten Signal in dB. Der Klirrfaktor eines Audiogeräts gibt an, in 

welchem Maße einem sinusförmigen Eingangssignal (Messton) durch nichtlineare Verzerrungen 

unerwünschte Obertöne bzw. Harmonische zugefügt werden. Er ist also ein Maß für die 

auftretenden harmonischen Verzerrungen. 

k = 

U 

2 

1 

U 

2 

2 

+ U 

+ U 

2 

2 

2 

3 

+ U 

+ U 

2 

3 

2 

4 

+ U 

+ ... + U 

2 

4 

2 

υ 

+ ... + U 

Zeigerdarstellung der Leistungen: 

+ ... + U 

1 

U 

+ U 

D 

2 

+ U 

+ ... + U 

2 

2 2 2 

2 

n 

2 

2 

υ + ... + Un 

⋅100% 

= 

2 3 4 

2 

U 

υ 

THD = Dk 

= 20dB ⋅log10 

k 

D 

P 

Q 

S 

Q1 

+ ... + U 

2 

n 

⋅100%

32 

Liniendiagramme verschiedener Oberschwingungsströme bei sinusförmiger Spannung: 

Λ 

u = u sinωt 

, i = i sin 3ω 

t 

p ( t ) = u sinω 

t ⋅ i sinν 

⋅ ω t 

ν 

Λ 

p ( t ) = u ⋅ i ⋅ sinω 

t ⋅ sinν 

⋅ ω t 

ν 

n 

∑ 

ν = 1 

Λ 

T 

0 

Λ 

1 

P = p ( t ) dt = P 

T ∫ ν 

Λ 

Λ 

Λ Λ 2π 

1 

2 

1 

P1 = ⋅ u⋅ 

i1 

sin t ⋅ d 

⋅ 

2 ∫ ω 

π 

2 

0 

Für alle ν ungleich 1 gilt: 


1 

Λ Λ 

( ωt 

) = ⋅ u ⋅ i1 

= U I1 

T 

1 

= ∫ p ( t ) dt = 0 

T 

Pν ν 

0 

Allgemein gilt: Nur die Grundschwingung des Stromes ist Träger der Wirkleistung 

= Λ 

i 

[ sin ω t + 1 3 sin( 

3ωt 

) + 1 5 sin( 

5t 

) + 1 7 sin( 

7 t ) + ... ] 

i ω 

Oberschwingungsbehafteter Strom bestehend 

aus Grundschwingung + 3. bis 11. Oberschwin- 

sinusförmige Spannung 

gung, Leistungsmaximum = 1,00 p.u. 

Man erkennt, dass die aus der Summe aller Teilleistungen 

der Grund- und Oberschwingungen 

gebildete rote Leistungsfläche Flächengleich der 

allein aus der Grundschwingung des Stromes 

mit der sinusförmigen Spannung gebildeten grünen 

Leistungsfläche ist. 

Stromaufnahme kapazitiver Netzgeräte 

(z. B. Fernseher, Computer, Energiesparlampen, 

Ladegeräte): 

i ges 

= i 

Λ 

Λ 

u = u sinω 

t 

Effektivwert der Spannung: 

Λ 

Λ 

U = u / 2 = 0, 

707u 

Normierung p.u. 

Λ 

Leistung: 

Funktionswert 

1,00 

0,75 

0,50 

0,25 

0,00 

-0,50 

-0,75 

-1,00 

Funktionswert 

Funktionswert 

1,00 

0,75 

0,50 

0,25 

0,00 

-0,25 

-0,50 

-0,75 

-1,00 

1,00 

0,75 

0,50 

0,25 

0,00 

-0,25 

-0,50 

-0,75 

-1,00 


Spannung Sinus Strom 3. Oberschwingung Leistung 

0 30 60 90 120 150 180 210 240 270 300 330 360 

Argument 


Grundschwingungsstrom + 3.+5.+7.+9.+11. Oberschwingung 

Leistung aus Grundschwingungsstrom 

Leistung aus Synthesestrom 

Strom als Rechteckfunktion 

0 30 60 90 120 150 180 210 240 270 300 330 360 

Argument 

( 0, 27sinω 

t − 0, 

19sin3ω 

t + 0, 

19sin5ω 

t − 0, 

13sin7ω 

t + 0, 

11sin9ω 

t − 0, 

11sin11ω 

t ) 

u 

i 

u = = 1 i = = 1 

U 

I 

0 

() t = u() 

t i() 

t 

p ⋅ 

Funktionswert 

1,00 

0,75 

0,50 

0,25 

-0,75 

-1,00 

Λ 

0 


Spannung Strom Grundschwingung Leistung 

0,00 

0 

-0,25 

-0,50 

30 60 90 120 150 180 210 240 270 300 330 360 

Argument 


sinusförmige Spannung (Effektivwert = 0,707 p.u.) 

Grundschwingungsstrom + 3.+5.+7.+9.+11. Oberschwingung 

Leistung aus Grundschwingungsstrom 

Leistung aus Analysestrom 

Leistungsmittelwert = 0,14 p.u. 

Effektivwert des Stromes = 0,31 p.u. 

0 30 60 90 120 150 180 210 240 270 300 330 360 

-0,25 

Argument

33 

6.2 Resonanzwirkungen in oberschwingungsbehafteten Netzen 

6.2.1 Resonanz zwischen Einspeisetrafo und Blindleistungskompensationsanlage 

Schaltplan einer Last mit 

Kompensationskondensator, Ersatzschaltplan: 

uk = 4% 


RY ist der Phasenwiderstand 

und CY ist die Phasenkapazität der Ersatz-Sternschaltung. 

Zunächst soll der Widerstand RY unbeachtet bleiben. Dann gilt für die Resonanzfrequenz der Reihenschaltung 

aus Induktivität und Kapazität (Reihenresonanz mit Blindwiderstand X=0) bei der 

Resonanzfrequenz fR: 

Mit X k ≈ Zk 

gilt: 

f 

R 

1 

= ⋅ 

2π 

U 

L 

k 

1 

⋅C 

Y 

, 

L 

X 

Q 

k 

C 

k = , CY 

= 2 

ωn 

ωn 

⋅U 

n 

k X k = , Für die Kurzschlussspannung des Transformators gilt: 

In 

uk 

Un 

Uk = ⋅ 

100 3 

u k ist die relative Kurzschlussspannung. Sie wird als Prozentwert angegeben. 

Bei Ortsnetztransformatoren ist z.B. u k = 4% 

. Bei Hochspannungstransformatoren ist u k = 10% 

. 

Die Kurzschlussspannung ist diejenige Spannung, die bei kurzgeschlossener Unterspannungsseite 

oberspannungsseitig angeschlossen werden kann, damit der Strom in beiden Wicklungen gleich 

dem Nennstrom wird. So lässt sich im Prüffeld das thermische Verhalten auch bei niedriger Leistung 

prüfen. 

Uk 

QC 

uk 

Un 

1 QC 

uk 

1 1 QC 

uk 

QC 

Lk 

⋅CY = ⋅ = ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ = ⋅ 

2 

2 

2 

ω ⋅ I ω ⋅U 

100 3 ω ⋅ I ω ⋅U 

100 3 ω ⋅ I ω ⋅U 

100 ω ⋅ S 

n 

n 

U = Un 

n 

R C 

Damit ergibt sich für die Resonanzfrequenz: 

n 

n 

n 

n 

n 

100 S 

fR = fn 

⋅ ⋅ 

u Q 

2 

UY 

Mit Berücksichtigung des Lastwiderstandes RY ergibt sich mit der LastP 

= 3 ⋅ 

RY 

( ) 

( ) 

2 

Un 

= folgendes: 

RY 

2 

1 

RY 

⋅ 

jωCY 

RY 

RY 

⋅ 1− 

jωCY 

RY 

Z = jωLk 

+ = jωLk 

+ 

= jωLk 

+ 

1 

jωCY 

RY 

+ 1 

R + 

1+ 

ωCY 

RY 

jωCY 

Resonanz liegt vor, wenn der Imaginärteil verschwindet, also Im { Z} = 0 wird. 

( ) 2 

2 

ω ⋅CY 

⋅ RY 

ω ⋅ Lk 

= 

⇒ ( ) 

1+ ω ⋅CY 

⋅ RY 

2 

2 

CY 

⋅ RY 

= 1+ ω ⋅CY 

⋅ R ⇒ 

Y 

Lk 

( ) ⎟ 2 

ω = 

CY 

1 

2 

⋅ RY 

⎛ C 2 ⎞ 

Y ⋅ ⎜ ⋅ RY 

− 1 

⎝ Lk 

⎠ 

2 1 

ω = 

Lk 

⋅CY 

⎛ Lk 

⋅ 

⎜ 

⎜1− 

2 

⎝ RY 

⋅CY 

⎞ L 

⎟ , k 

2 

⎠ RY 

⋅CY 

2 

uk 

Un 

= ⋅ 

100 ωn 

⋅ Sn 

1 

⋅ 2 

RY 

2 

2 

ωn 

⋅U 

n uk 

Un 

⋅ = ⋅ 

QC 

100 ωn 

⋅ Sn 

P 

⋅ 4 

Un 

2 

ωn 

⋅U 

n ⋅ 

QC 

2 

2 1 ⎛ u 

⎞ 

⎛ 

⎞ ⋅ ⎛ 

k P 100 ωn 

⋅S 

n uk 

P 

2 100 Sn 

uk 

P 

ω = ⋅ 

⎜ 

⎜1− 

⋅ 

⎟ = ⋅ ⋅ 

⎜ 

⎜1− 

⋅ 

⎟ = ω ⎜ 

n 1− 

⋅ 

Lk ⋅CY 

⎝ 100 ⋅S 

n ⋅QC 

⎠ uk 

QC 

⎝ 100 ⋅S 

n ⋅QC 

⎠ uk 

⋅QC 

⎝ 100 Sn 

⋅Q 

Allgemein gilt somit für die Resonanzfrequenz: fR 

= fn 

⋅ 

100 ⋅ S ⎛ 

⎞ 

n uk 

P 

⎜ 

⎜1− 

⋅ 

⎟ 

uk 

⋅QC 

⎝ 100 Sn 

⋅QC 

⎠ 

Beispiel: Ortsnetztransformator 630 kVA, uk = 4 %, P = 500 kW, QC=250 kVar: 

fR 

= fn 

⋅ 

100 Sn 

⋅ 

uk 

QC 

= 50Hz 

100 ⋅ 630 

= 397Hz 

, fR 

4 ⋅ 250 

= fn 

⋅ 

100 ⋅ S ⎛ uk 

P ⎞ 

n 

1 

384Hz 

uk 

Q ⎜ − ⋅ = 

C 100 Sn 

Q ⎟ 

⋅ ⎝ 

⋅ C ⎠ 

Durch die ohmsche Last wird die Resonanzfrequenz geringfügig um 3,4 % erniedrigt. 

Xk 

Un 3 

RY CY 

k 

n 

C 

n 

Widerstand in Ohm 

n 

0,2 

0,0 

-0,2 

-0,4 

-0,6 

-0,8 

Blindwiderstand X=XL-XC Reihenresonanz 

Trafo mit Kompensationsanlage 

n 

XL XC X = XL+XC f Resonanz 

50 150 250 350 450 550 650 

Frequenz in Hz 

n 

C 

⎞ 

⎟ 

⎠ 

n 

n

34 

6.2.2 Verdrosselung der Blindleistungkompensationsanlage 


C 

Ersatzschaltplan für die Oberrschwingungeinspeisung 

des Stromrichters 

IK 

, h 

IL, 

h 

ZN, 

h 

= 

ZN, 

h + ZK 

, h 

mit der Netzimpedanz: ZN, 

50Hz 

2 

UN 

= uk 

Sn, 

T 

u k als per unit -Wert (p.u.) 

2 

UN 

für Oberschwingung h ist die Netzimpedanz: ZN, 

h = uk 

Sn, 

T 

h 0,8 

p = 4 7 14 % 

Für den verdrosselter Kompensationszweig gilt: 

0,6 

X K = X LD − X C , 

0,4 

X LD 

mit dem Verdrosselungsfaktor p = 

X C 

2 

= ω n ⋅ LD 

⋅CY 

folgt: 

0,2 

0,0 

2 

U n 

X C = , für die Oberschwingung h: X C, 

h 

QC 

1 

= ⋅ X C 

h 

2 

1 Un 

= ⋅ , 

h QC 

2 

UN 

X LD = p ⋅ X C = p ⋅ , für die Oberschwingung h: X LD, 

h 

QC 

2 

U n 

= p ⋅ h ⋅ X C = p ⋅ h ⋅ 

QC 

2 

U n ⎛ 1 ⎞ ω 

X k, 

h = X LD, 

h − X C, 

h = ⎜ p ⋅ h − ⎟ , h = , QLC 

Q ⎝ h ⎠ ω 

= 

X 

2 

U 

− X 

= 

X 

2 

U 

− p ⋅ X 

= 

Q 

n 

C 

Ik / IL 

Saugwirkung einer verdrosselten 

Kompensationsanlage für die 7. Oberschwingung 

0,0 0,2 0,4 0,6 0,8 1,0 

Qc / Sn,T 

LD 

C 

C 

C 

( 1− 

p) 

QLC ist die kapazitive Blindleistung der verdrosselten Kompensationsanlage. (s. Grossmann, etz 5/2008) 

Damit folgt für das Verhältnis des von der Kompensationsanlage abgesaugten Oberschwingungs- 

stromes zu dem vom Stromrichter emittierten Oberschwingungsstrom der Ordnung h: 

2 

Un 

QC 

Q 

uk 

⋅ h ⋅ 

uk 

⋅ 

uk 

⋅ ( 1− 

p) 

⋅ 

IK 

, h ZN, 

h 

Sn, 

T 

Sn, 

T 

S 

= 

= 

= 

= 

2 2 

I 

1 

, Z , Z , U U 1 Q 

Q 

L h N h + K h 

n n ⎛ ⎞ 

C 

u h 

p h uk 

p u 1 p 

k ⋅ ⋅ + ⎜ ⋅ − ⎟ ⋅ + − 2 k ⋅ − ⋅ 

S Q ⎝ h ⎠ Sn, 

T h 

Sn, 

T 

n, 

T 

C 

LC 

n, 

T 

1 

h 

LC ( ) + p − 2 

Durch die Verdrosselung wird die Resonanzfrequenz der Kompensationsanlage mit dem Einspeisetransformator 

zu niedrigeren Werten verschoben: 

ω 

Mit h = , ergibt sich die Resonanz- 

Blindwiderstand X=XL-XC Reihenresonanz Trafo 

ωn 

mit Kompensationsanlage 

frequenz, wenn man den Nenner gleich 

Null setzt, mit ω = ωR 

zu: 

0,2 

ω = ω ⋅ 

R 

n 

u 

S 

k 

nT 

⋅Q 

C 

1 

⋅ 

Sn, 

T 

1+ 

p ⋅ 

u ⋅Q 

Mit den vorstehenden Daten ergibt sich 

bei p = 7 % für die Resonanzfrequenz 

fR = 170, 

6 Hz gegenüber 

= 396, 

9Hz 

ohne Verdrosselung. 

f R 

uk = 4% 

U = Un 

M 

k 

LD 

C 

C 

⋅ 

IL 

IL,h 

Xk 

Widerstand in Ohm 

0,0 

-0,2 

-0,4 

-0,6 

-0,8 

Ik,h 

LD 

CY 

XL XC X = XL+XC f Resonanz XL+XCD 

Resonanzfrequenz bei 

7 % Verdrosselung 

Resonanzfrequenz 

ohne Verdrosselung 

50 150 250 350 450 550 650 

Frequenz in Hz

35 

6.3 Allgemeine Bestimmungsgleichungen im Drehstromnetz, Stern-Dreieckumwandlung 

a) für Dreieck-Stern-Umwandlung 

L1 

L2 

L3 

U12 U31 

U23 

U12 

U23 

Z 

I1 

I2 

U31 

I3 

I2 

L1 

L2 

U2 

L3 

Mp 

I1 

I3 

U3 

Z 

U1 

Z1=R 

Z2=R 

Z3=R 

Z12 

Z23 

⋅ Z 

12 31 

1 = , 

Z 12 + Z 23 + Z 31 

b) für Stern-Dreieck-Umwandlung 

Z1 

Z2 

Z3 

Z0 


I1 

I2 

I3 

I0 

Z31 

Z 

∆ - Ү 

Z0 → 

Z 

∞ 

⋅ Z 

23 12 

2 = , 

Z 12 + Z 23 + Z 31 

Ү - ∆ 

L1 

L2 

U2 

L3 

Mp 

Z 

U3 

3 

U12 

U23 

U1 

= 

Z 

12 

I1 

I2 

I3 

U31 

I0 

I2 

23 

I1 

I3 

Z1 

Z2 

Z3 

Z0 

Z 31 ⋅ Z 23 

+ Z + Z 

Z 1 ⋅ Z 2 

Z 12 = Z 1 + Z 2 + , Z 23 

Z 3 

Leiterströme im Dreileitersystem: 

Z 2 ⋅ Z 3 

= Z 2 + Z 3 + , Z 31 = Z 3 

Z 1 

Z 3 ⋅ Z 1 

+ Z 1 + 

Z 2 

In einem Dreileiter-Drehstromnetz muss der Widerstand Z0 im Mittelpunktleiter gleich unendlich 

gesetzt werden (I0 = 0), so dass für die drei Bestimmungsgleichungen der Leiterströme gilt: 

I 

I 

I 

1 

2 

3 

U 

= 

1 

U 

= 

U 

= 

2 

3 

Z 2 + Z 3 ) − ( U 2 Z 3 + U 3 Z 2 ) 

( Z 1 Z 2 + Z 2 Z3 

+ Z 3 Z 1) 

( Z 3 + Z 1) 

− ( U 3 Z 1 + U 1 Z 3 ) 

( Z 1 Z 2 + Z 2 Z 3 + Z 3 Z 1) 

( Z 1 + Z 2 ) − ( U 1 Z 2 + U 2 Z 1) 

( Z Z + Z Z + Z Z ) 

( 

1 

2 

2 

Ein Beispiel ist die Symmetrierschaltung im Induktionsofenbau (Steinmetz-Schaltung): 

L1 

L2 

L3 

U12 U31 

U23 

I1 

I2 

I3 

3 

UPh 

U 

Für die Leiterströme gilt: I1 

= I2 

= I3 

= = wenn X = 3 ⋅R 

ist. 

R 3 ⋅R 

Die Ströme sind in Phase mit den zugehörigen Phasenspannungen, d.h. die Schaltung wirkt wie 

eine rein ohmsche Last mit dem Widerstand R. Der Strom I1 ist unabhängig von der Größe des 

Widerstandes Z1 = R, da Z2 = - Z3 ist! Da die Induktionsspule zur Erzeugung des Wechselfeldes im 

Schmelzmaterial ein ohmsch-induktiver Widerstand ist, muss dieser durch eine gesteuerte Parallelkompensation 

auf cos φ = 1 kompensiert werden. 

3 

Z1=3R 

Z2=jX 

Z3=-jX 

1 

L1 

U12 

L2 

U23 

L3 

∼ 

∼ 

∼ 

L1 

U1 

L2 

U2 

L3 

U3 

U31 

I3 

I2 

I1 

31 

Z12 

Z23 

I1 

I2 

I3 

Z12=jX 

Z23=R 

Z1 

Z2 

Z3 

X= 3 R 

Z31 

Z31=-jX

36 

6.4 Belastung des Transformators mit maximalem Wirkungsgrad 

2 

S P 

Pv = P0 

+ 3 ⋅ I ⋅ Rk 

, I = = 

, 

U ⋅ 3 U 3 ⋅ cosϕ 

Für den Wirkungsgrad gilt: 


η 

P 

P 

= = 

2 

P + Pv 

P + P0 

+ 3 ⋅ I 

2 2 

P 

P ⋅U 

⋅ cos ϕ 

η = = 

= f ( P) 

2 

2 2 

2 

⎛ P ⎞ ( P + P0 

) ⋅U 

⋅ cos ϕ + Rk 

⋅ P 

P + P + ⋅ R ⎜ 

⎟ 

0 3 k ⋅ 

⎜ 

U 

⎟ 

⎝ 3 ⋅ cosϕ 

⎠ 

Um das Maximum zu finden wird die Funktion f(P) nach P differenziert und gleich Null gesetzt: 

dη 

U 

= 

dP 

2 

2 

⋅ cos ϕ ⋅ 

dη 

= 0 ⇒ η = η 

dP 

[ ] [ ( ) 

] 

[ ] 2 

2 2 

2 2 2 

2 2 

( P + P0 

) ⋅U 

⋅ cos ϕ + Rk 

⋅ P − U ⋅ cos ϕ + 2 ⋅ P ⋅ Rk 

⋅ P ⋅U 

⋅ cos ϕ 

2 2 

2 

( P + P ) ⋅U 

⋅ cos ϕ + R ⋅ P 

max 

0 

2 2 

2 2 

⋅ [ ( P + P0 

) ⋅U 

⋅ cos ϕ + R ⋅ Pk 

] = [ U ⋅ cos ϕ + 2 ⋅ P ⋅ R ] ⋅ P ⋅ 

2 2 

cos ϕ 

( 2 2 

+ P ) ⋅U 

⋅ cos ϕ + R 

2 

⋅ P 

2 2 

= U ⋅ cos ϕ + 2 ⋅ P ⋅ R ⋅ 

2 

⋅ cos ϕ 

U ⋅ 

2 

U k 

[ ] [ ] P 

P 0 

k 

k 

P 

2 

2 2 

2 

2 

P ⋅U 

⋅ cos ϕ + R ⋅ P = 2 ⋅ P ⋅ R 

0 

k 

2 2 2 

P ⋅U 

⋅ = P ⋅ R 

0 cos ϕ 

k 

2 2 

2 P0 

⋅U 

⋅ cos ϕ 

P = , Rk 

Rk 

= 

Pk 

2 

⋅ I 

2 2 

2 

2 2 

P0 

⋅U 

⋅ cos ϕ ⋅ 3 ⋅ In 

P0 

⋅ Sn 

⋅ cos ϕ 2 2 

= = 

= S ⋅ cos ϕ 

P 

P 

k 

P0 

S = ⋅ S 

P 

Anwendungsbeispiel: 

Ortsnetztransformator mit Sn = 630 kVA Nennleistung, Un =400V, cosφ=0,9 

weist im Prüfprotokoll folgende Daten aus: P0=1.350 W, Pk=7.000 W 

P0 

1. 

350 

S = ⋅ Sn 

= ⋅ Sn 

= 0, 

44 ⋅ Sn 

= 44% 

⋅ S 

P 7. 

000 

η 

k 

P 

P 

= = 

= 

= 

2 

2 

P + Pv 

P + P0 

+ 3 ⋅ I ⋅ Rk 

S ⋅ cosϕ 

+ P0 

+ 3 ⋅ 

ϕ 

n k 

k 

n 

k 

n 

k 

S ⋅ cosϕ 

Allgemein gilt für den Lastfaktor a = S/Sn = (P/cosφ)/Sn: 

η 

max 

= 

0, 

44 

⋅ S 

n 

0, 

44 

⋅ S 

⋅ cosϕ 

+ P 

0 

n 

η 

⋅ cosϕ 

+ 3 ⋅ 

a ⋅ S 

⋅ cosϕ 

n 

= 2 

a ⋅ Sn 

⋅ cosϕ 

+ P0 

+ a 

( 0, 

44 ⋅ I ) 

n 

2 

⋅ R 

k 

= 

0, 

44 

k 

3 n 

S ⋅ cosϕ 

⋅ R 

2 ( a ⋅ I ) ⋅ R S ⋅ cos + P0 

+ a ⋅ Pk 

⋅ S 

⋅ P 

k 

0, 

44 ⋅ Sn 

⋅ 0, 

9 

⋅ 0, 

9 + P + o, 

44 

η 98, 

93% 

bei cosφ = 0,9 , η 99, 

03% 

bei cosφ = 1 

max = 

max = 

n 

0 

2 

⋅ P 

k 

= 

k 

98, 

93 

%

7. Leitungsnetzberechnung 

7.1 Allgemeine Leitungsgleichungen 

Herleitung der Leitungsgleichungen 

x = x1 x 

∂u 

i i G′ 

⋅dx 

⋅u 

+ C′ 

1 = 2 + 

2 ⋅dx 

⋅ 

∂t 

∂i1 

u 1 = i1 

⋅R 

′ ⋅dx 

+ L′ 

⋅dx 

⋅ + u2 

∂t 


2 

37 

∂i 

∂u 

− = G′ 

⋅u 

+ C′ 

⋅ 

∂x 

∂t 

∂u 

∂i 

− = R′ 

⋅ i + L′ 

⋅ 

∂x 

∂t 

2 

∂ u ∂i 

∂ ∂i 

− = R′ 

⋅ + L′ 

⋅ ⋅ 

2 

∂x 

∂x 

∂t 

∂x 

2 

⎛ ∂u 

⎞ ⎛ ∂u 

∂ u ⎞ 

= −R 

′ ⋅ ⎜G′ 

⋅u 

+ C′ 

⋅ ⎟ − L′ 

⋅ ⎜ 

⎜G′ 

⋅ + C′ 

⋅ ⎟ 

2 

⎝ ∂t 

⎠ ⎝ ∂t 

∂t 

⎠ 

Dies führt zur Leitungs-Wellengleichung oder Telegraphengleichung: 

2 

2 

∂ u ∂ u 

∂u 

= L′ 

⋅C′ 

⋅ + ( R′ 

⋅C′ 

+ G′ 

⋅L′ 

) ⋅ + R′ 

⋅G′ 

⋅u 

, ( ) { } 

2 

2 

∂x 

∂t 

∂t 

t jω 

u = f x, 

t = Re 2 ⋅U 

⋅e 

, uˆ = 2 ⋅U 

Für die sinusfömigen Spannungen u(t) und die Ströme i(t ) gilt in der komplexen Ebene mit den 

jϕu 

jϕi 

Zeigergrößen: U = U ⋅e 

, I = I ⋅e 

(U und I sind die Effektivwerte der entsprechenden Größen): 

u() 

t = 

jωt 

∂u 

2 ⋅U 

⋅e 

, = jω 

⋅ 

∂t 

jωt 

2 ⋅U 

⋅e 

, i( 

t ) = 

jωt 

∂i 

2 ⋅I 

⋅e 

, = jω 

⋅ 

∂t 

jωt 

2 ⋅I 

⋅e 

, 

∂ 

∂t 

2 

u 2 

jωt 

= −ω 

⋅ 2 ⋅U 

⋅e 

2 

2 

∂ 

∂x 

j t 

[ ω + R′ 

G′ 

] ⋅ 2 ⋅U 

⋅e 

u ω 

2 

2 

, = − L′ 

C′ 

⋅ + jω( 

R′ 

C′ 

+ G′ 

L′ 

) 

2 

d U 

= ( R′ 

+ jω 

⋅L′ 

) ⋅ ( G′ 

+ jω 

⋅C′ 

) ⋅U 

2 

dx 

Diese Leitungsgleichung ist eine Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten, 

für die der Lösungsansatz gilt: 

γ ⋅x 

U γ ⋅x 

U = U 0 ⋅e 

, = U ⋅γ 

⋅e 

x 

2 

2 

d 

2 0 

Aus diesem Ansatz folgt für die komplexe Konstanteγ : 

d 

U 

0 

⋅ 

2 γ ⋅x 

⋅e 

= ( R′ 

+ jω 

⋅L′ 

) ⋅ ( G′ 

+ jω 

⋅C′ 

) ⋅U 

γ ⋅x 

⋅e 

( R ′ + jω 

⋅L′ 

) ⋅ ( G′ 

+ j ⋅C′ 

) , γ = ± ( R′ 

+ jω 

⋅ L′ 

) ⋅ ( G′ 

+ jω 

⋅C′ 

) = ± γ 

γ 0 

γ = ω 

2 

1, 

2 

= 

γ nennt man die Fortpflanzungskonstante, ZW ist der Wellenwiderstand der Leitung. 

γ α + jβ 

α ist der Dämpfungsbelag (Dämpfungskonstante), β ist der Phasenbelag (Phasenkonstante) der 

Leitung. Allgemeine Lösung der Leitungsgleichung: 

−γ 

⋅x 

+ γ ⋅x 

U( 

x) 

= U v ⋅ e + U r ⋅ e 

Dies ist die Summe aus einer vorlaufenden und einer rücklaufenden Spannungswelle. 

∂u 

δ i ∂U 

Wegen: − = R′ 

⋅ i + L′ 

⋅ oder − = ( R′ 

+ jω 

L′ 

) ⋅I 

folgt für den Strom I : 

∂x 

δ t ∂x 

I 

i1 = i(x,t) 

u1 = u(x,t) 

G′ 

+ jωC′ 

−γ 

⋅x 

+ γ ⋅x 

( x) 

= 

⋅ ( U v ⋅e 

−U 

r ⋅e 

) 

R′ 

+ jωL′ 

R'dx 

L'dx 

C'dx 

mit 

Somit folgt für den Strom: I( 

x) 

Z W 

U 

= 

Z 

v 

W 

= 

G'dx 

⋅e 

R′ 

+ jωL′ 

G′ 

+ jωC′ 

−γ 

⋅x 

x = x2 = x+dx 

U 

− 

Z 

i2 = i[(x+dx),t] = i1 + di 

u2 = u[(x+dx),t] = u1 + du 

r 

W 

⋅e 

als Wellenwiderstand. 

+ γ ⋅x

38 

Herleitung der hyperbolischen Form der Leitungsgleichungen 

Am Leitungsende gilt für x = l: 

−γ 

⋅l 

+ γ ⋅l 

−γ 

⋅l 

U = U ⋅ e + U ⋅ e 

U + Z ⋅I 

= 2U 

⋅ e 

Z 

W 

⋅I 

2 

2 

= U 

v 

v 

⋅ e 

−γ 

⋅l 

− U 


r 

r 

⋅ e 

+ γ ⋅l 

U 

2 

2 

− Z 

W 

W 

⋅I 

2 

2 

v 

= 2U 

Daraus folgt für die Spannung der vorlaufenden Welle: U v 

U 2 + Z W ⋅I 

2 

= 

2 

+ γ ⋅l 

⋅ e 

Entsprechend für die Spannung der rücklaufenden Welle: U r 

Am Leitungsanfang gilt für x = 0: 

U 2 − Z W ⋅I 

2 

= 

2 

−γ 

⋅l 

⋅ e 

v r U U U + = 

U v 

1 , I 1 = 

Z 

U r 

− 

Z 

Somit für die Spannung am Leitungsanfang: 

U 

1 

= U 

v 

+ U 

r 

U 

= 

2 

+ Z 

2 

W 

⋅I 

2 

⋅ e 

U = U γ ⋅ l + Z W ⋅I 

sinhγ 

⋅ l 

W 

W 

− Z 

2 

+ e 

2 

r 

⋅ e 

+ γ ⋅l 

+ γ ⋅l 

−γ 

⋅l 

+ γ ⋅l 

+ γ ⋅l 

U 2 W ⋅I 

2 −γ 

⋅l 

e 

e − 

+ 

⋅ e = U 2 

+ Z W ⋅I 

2 

1 2 cosh 2 , U( x) 

= U 2 coshγ ⋅( 

l − x) 

+ I 2 ⋅ Z W ⋅ sinhγ 

⋅( 

l − x) 

I 1 = 

U 2 

U 2 

I 2 coshγ 

⋅ l + ⋅ sinhγ 

⋅ l , I( 

x) 

= I 2 coshγ 

⋅( 

l − x) 

+ ⋅ sinhγ 

⋅( 

l − x) 

Z W 

Z W 

Sonderfälle: 

a) nur Längswiderstände: γ = ± ( R′ + jω 

⋅L′ 

) ⋅ ( G′ 

+ jω 

⋅C′ 

) = 0 , Z W = 

R′ 

+ jω 

L′ 

= ∞ 

G′ 

+ jωC′ 

I1 

U1 

x = 0 

e 

2 

−γ 

⋅l 

Die Unbestimmtheit des Produktes im zweiten Term 

der Spannungsgleichung ergibt sich aus der 

3 

2 

Reihenentwicklung: x 

x 

sinh x = x + + ... cosh x = 1+ 

+ ... 

3! 

2! 

zu: sinh γ ⋅ l = R + jωL 

, so daß gilt: 

( R + j ⋅ L) 

I 2 

1 = U 2 + ω , 1 2 

U ⋅ 

b) verlustlose Leitung, fürR ′ = 0 und G′ 

= 0 ergibt sich: γ = ( R ′ + jω 

⋅L′ 

)( ⋅ G′ 

+ jω 

⋅C′ 

) = α + jβ 

, 

α = 

Mit 

I1 

0 

U1 

R=R'·l 

x = 0 

0 

x 

L=L'·l 

I = 

2 ( ω ⋅ ′ ⋅C′ 

) = jβ 

= j ⋅ L′ 

⋅C 

γ = − L ω ′ , 

L′ 

L 

Z , 

v = 

W = 

ZW 

= = 

C=C'·l U2 

C′ 

C 

1 

= 

L′ 

⋅C 

′ 

c 

µ r ⋅ ε r 

v ist die Wellen, c ist die Lichtgeschwindigkeit 

1 

c = und c = λ ⋅f 

folgt: 

µ ⋅ ε 

0 

x 

L=L'·l 

U2 

x = l 

x = l 

I2 = I1 

1 c 1 

1 

β = 2π ⋅ ⋅ = 2π 

⋅ ⋅ µ ⋅ ε ≈ 2π 

, 

r r 

λ v λ 

λ 

Damit ergibt sich für die Spannung und den Strom 

am Leitungsanfang der verlustlosen Leitung: 

l L 

l 

U 1 = U 2 cos 2π 

⋅ + j ⋅ ⋅I 

2 sin2π 

⋅ 

λ C λ 

l C 

l 

I 1 = I 2 cos2π ⋅ + j ⋅ ⋅U 

2 sin2π 

⋅ 

λ L 

λ 

I2 

jx − jx 

e − e 

sinh jx = = j sin x 

2 

2.000 

U2 

1.000 

0 

-1.000 

I 

jx − jx 

e + e 

cosh jx = = cos x 

2 

Spannung und Strom bei Leerlaufbetrieb: 

Spannung U am Leitungsende und Strom am 

Leitungsanfang in Abhängigkeit von der 

Leitungslänge bei U1 = 400 kV, f = 50Hz 

Spannung U2 Strom I1 

2.000 

I1 

1.000 

-1.000 

-2.000 

-2.000 

0 1500 3000 Länge 4500 in km 6000 

0

7.2 Spannungsfallberechnung auf Leitungen 

Einphasiger Ersatzschaltplan: 

~ 

0 

Gleichmäßig verteilte Last p in kW/m 

I1 I(x) 


l 

39 

Für Höchstspannungsleitungen: Für Hoch- Mittel- und Niederspannungsleitungen: 

I1 

R L 

I2 

R X I 

U1 

Zeigerdiagramm: Drehstromleistung; 

P = P2 

= 3 ⋅U 

2 ⋅ I ⋅ cosϕ 

= 3 ⋅U 

n ⋅ I ⋅ cosϕ 

Spannungen: 

U l = I ⋅ R ⋅ cosϕ + I ⋅ X ⋅ sinϕ 

U q = I ⋅ X ⋅ cosϕ − I ⋅ R ⋅ sinϕ 

∆U 

= 

2 

U l 

2 

+ U q ≈ U l 

U l 

U l 

= I ⋅ cos ϕ ⋅ 

= I ⋅ cos ϕ ⋅ψ 

⋅ l = 

tanϕ 

P 

⋅ψ 

⋅ l , ψ = R `+ X`⋅ 

tanϕ 

3 ⋅U 

n 

Mit dem relativen Spannungsfall: ul 

= 

⋅U 

l 

U n 

3 

Re 

U1 

Uq 

φ 

I jX 

Ul 

φ I R 

δ 

U2=U2 

I 

φ 

folgt: 

j 

1 

∆u ≈ ul 

= 2 

U 

100% 

⋅ P ⋅ψ 

⋅ l = ⋅ P ⋅ψ 

⋅ l 

2 

U 

x l 

n 

( R + X ⋅ tanϕ 

) = I ⋅ cosϕ 

⋅ ( R`+ 

X`⋅ 

) ⋅ l 

Für eine Leitung mit gleich bleibenden Leitungsdaten und mehreren Lastentnahmen gilt: 

~ 

C/2 

G/2 C/2 

I1 

l2 

Für eine Leitung mit gleichmäßig verteilter Last gilt: 

n 

(Hier ist P1 die Summe aus verteilter Last plus P2) 

lk 

P1 P2 Pk 

G/2 

mit zusätzlicher Punktlast P2 am Leitungsende gilt: 

100% P1 

+ P2 

∆u = ⋅ψ 

⋅ l ⋅ 

mit 

2 

P 1 = 

p ⋅ l + P 

U 

2 

U2 

n 

100% 

∆u 

= 

U 

P = p ⋅ l 

1 , 

2 

n 

⎛ x ⎞ 

I 1− 

⎝ 

I 

⋅ψ 

⋅ 

1 

= 

n 

∑ 

k = 1 

P 

k 

3 ⋅U 

⋅ l 

P 

n 

1 

k 

⋅ cosϕ 

⎛ x ⎞ 

− 

⎝ 

( x) 

= I1 

⋅ ⎜ ⎟ , P( x) 

= P1 

⋅ ⎜1 

⎟ 

l ⎠ 

l ⎠ 

100% P1 

∆u = ⋅ψ 

⋅ l ⋅ 

2 

U 2 

Bei der Leitung mit gleichmäßig verteilter Last ist der Spannungsfall halb so hoch, als wenn die 

Gesamtlast am Leitungsende wirksam ist. Dann wäre hier: P1 = P2. 

ln 

Pn 

U1 

2 

X=ωL 

n 

U2

40 

7.3 Lastflussberechnung 

7.3.1 Herleitung des Knotenpunkt-Potenzialverfahrens 

Einige Voraussetzungen für die Geltung und Anwendung des Verfahrens: 

1. Symmetrische Belastung im Drehstromnetz 

2. Annähernd gleiche Phasenwinkel der Spannungen (sonst Berechnung mit komplexen Größen) 

3. Annähernd gleiche Leistungsfaktoren der Lasten 

Bezeichnungen: Unbekannte Netzknotenpunktspannungen U1, U2,…Uk…Un 

Speisepunkte mit vorgegebene Spannungen: UI, UII,…Us,…Um 

Vorzeichenregel: zufließende Leistungen positiv, abfließende Leistungen negativ 

1 

2 

Pi,k 

i 

Pi 

k 


Für den Längsspannungsfall der Phasenspannungen gilt: 

∆U Ph = Ui 

, ph − Uk 

, ph = −Ii 

, k ⋅cosϕ 

⋅ψ 

⋅ l i, 

k , ψ = R `+ X`⋅ 

tanϕ 

Für den verketten Wert der Spannungen im Drehstromsystem 

gilt: ∆U = ( Ui 

− Uk 

) = − 3 ⋅I 

i, 

k ⋅ cosϕ 

⋅ψ 

⋅ l i, 

k , 

1 

mitλ 

= gilt: 

l ⋅ψ 

mit: P i, 

k = 3 ⋅U 

n ⋅I 

i, 

k ⋅ cosϕ 

gilt: 

∆U ⋅ λ i, 

k = − 

Pi 

, k 

3 ⋅I 

i, 

k ⋅cosϕ 

= − 

U 

P 

∆U ⋅ λ i, 

k = ( Ui 

−U 

k ) ⋅ λi, 

k = − 3 ⋅I 

i, 

k ⋅cosϕ 

= − 

U 

1 

n 

n 

n 

i 

∑ ( U i − U k ) ⋅ λ i, 

k = − ⋅∑ 

Pi 

, k = − mit: Pi 

= ∑ 

k = 1, 

k ≠i 

U n k = 1 U n 

k = 1 

n 

n 

Pi 

U i ⋅ ∑ λ − ∑U 

⋅ λi 

, k = − 

U 

i, 

k 

k 

k = 1, 

k ≠i 

k = 1, 

k ≠i 

Nun werden alle Punkte k, die Speisespannungen sind, herausgenommen und auf die rechte Seite 

n 

∑ 

k = 1, 

k ≠i 

der Gleichung gebracht und λ i k = λi 

i gesetzt: 

, 

n 

Ui ⋅ λ i, 

i − ∑U 

k ⋅ λi, 

k 

k = 1, 

k ≠i 

, k ≠s 

m 

= ∑U 

s ⋅ λi, 

k 

k = s= 

I 

Pi 

− 

Un 

explizit ergibt dies für k=3 und s=2 folgende Matrizengleichung: 

⎛ λ11 

⎜ 

⎜− 

λ21 

⎜ 

⎝− 

λ31 

− λ12 

λ22 

− λ32 

− λ13 

⎞ ⎛U 

1 ⎞ ⎛ λ1, 

I 

⎟ ⎜ ⎟ ⎜ 

− λ23 

⎟ ⋅ ⎜U 

2 ⎟ = ⎜λ 

2, 

I 

λ ⎟ ⎜ ⎟ ⎜ 

33 ⎠ ⎝U 

3 ⎠ ⎝λ 

3, 

I 

λ1, 

II ⎞ 

⎛ P1 

⎞ 

⎟ ⎛U 

⎞ ⎜ ⎟ 

I 1 

λ2; 

II ⎟ ⋅ ⎜ 

⎟ − ⋅ ⎜P2 

⎟ 

⎟ ⎝U 

II ⎠ U n 

λ 

⎜ ⎟ 

3, 

II ⎠ 

⎝P3 

⎠ 

Mit λi 

, k = 

1 

= 

⋅ψ 

l 

1 

⋅ R`+ 

X`⋅ 

tanϕ 

( ) 

, 

li , k 

i, 

k 

Wenn man beide Seiten der Gleichung mit dem Widerstandsbelag der Leitung ψ multipliziert, 

kann man an Stelle der Leitwerte auch die Kehrwerte der Längen mit l -1 einsetzen: 

− ⎛ l 

⎜ 

⎜− 

l 

⎜ 

⎝ 

− l 

1 

11 

−1 

21 

−1 

31 

UI 

− l 

l 

− l 

−1 

12 

−1 

22 

−1 

32 

− l 

−1 

13 

−1 

23 

1 

33 

− l 

− 

l 

⎞ ⎛U 

⎛ 1 ⎞ l 

⎟ ⎜ ⎟ ⎜ 

⎟ ⋅ ⎜U 

2 ⎟ = ⎜l 

⎟ ⎜ ⎟ ⎜ 

⎠ ⎝U 

3 ⎠ ⎝ 

l 

−1 

1, 

I 

−1 

2, 

I 

−1 

3, 

I 

n 

l 

l 

l 

−1 

1, 

II 

−1 

2, 

II 

−1 

3, 

II 

P 

⎞ 

⎟ ⎛U 

⎟ ⋅ ⎜ 

⎟ ⎝U 

⎠ 

Der Lastfluss zwischen den Punkten x und y ergibt sich zu: 

P 

Us 

x, 

y 

~ 

= − 

~ 

( U − U ) ⋅U 

⋅λ 

= − ( U − U ) 

x 

y 

n 

x, 

y 

x 

I 

II 

n 

⎛ P 

⎞ ψ ⎜ 

⎟ − ⋅ ⎜P 

⎠ U n ⎜ 

⎝P 

y 

U n 

⋅ 

l ⋅ψ 

x, 

y 

1 

2 

3 

P 

⎞ 

⎟ 

⎟ 

⎟ 

⎠ 

i, 

k 

i, 

k 

n

41 

7.3.2 Anwendung der Lastflussberechnung nach dem Knotenpunkt-Potenzialverfahren 

Ω 

Für das angegebene Niederspannungsnetz mit der Impedanz, ψ 

= R`+ 

X`⋅ 

tanϕ 

= 0, 

22 , Un =400 V 

km 

sollen der Lastfluss und die Knotenspannungen berechnet werden. 

Für die Leitwerte gilt: 1 1 1 

λ xy = = 

= ⋅ 4, 

55 Skm 

l Ω 

xy ⋅ψ 

l xy 

l xy ⋅ 0, 

22 

km 

Allgemeine Form der Matrizengleichung 

U I 

beim Knotenpunkt-Potenzialverfahren: UI = Un = 400 V 

100 kW 

205 m 

300 m 

1 

205 m 

3 

⎛ λ11 

⎜ 

⎜− 

λ21 

⎜ 

⎝− 

λ31 

− λ12 

λ22 

− λ32 

− λ13 

⎞ ⎛U1 

⎞ ⎛ λ1I 

⎞ ⎛ P1 

⎞ 

⎟ ⎜ ⎟ ⎜ ⎟ 1 ⎜ ⎟ 

− λ23 

⎟ ⋅⎜U 

2 ⎟ = ⎜λ2I 

⎟ ⋅U 

I − ⋅⎜ 

P2 

⎟ 

⎟ ⎜ ⎟ ⎜ ⎟ Un 

λ 

⎜ ⎟ 

33 ⎠ ⎝U 

3 ⎠ ⎝λ3 

I ⎠ ⎝P3 

⎠ 

225 m 

2 

200 kW 

100 m 

⎛λ1I 

+ λ 

⎜ 

⎜ − λ21 

⎜ 

⎝ − λ31 

13 

− λ 

2I 

− λ 

12 

λ + λ 

32 


23 

− λ13 

⎞ ⎛U 

1 ⎞ ⎛ λ1I 

⎞ ⎛ P1 

⎞ 

⎟ ⎜ ⎟ ⎜ ⎟ 1 ⎜ ⎟ 

− λ23 

⎟ ⋅ ⎜U 

2 ⎟ = ⎜λ 

2I 

⎟ ⋅U 

I − ⋅ ⎜P2 

⎟ 

+ + ⎟ ⎜ ⎟ ⎜ ⎟ U n 

λ 

⎜ ⎟ 

31 λ3I 

λ32 

⎠ ⎝U 

3 ⎠ ⎝λ3 

I ⎠ ⎝P3 

⎠ 

An Stelle der Lambda-Werte kann man auch die Kehrwerte der Leitungslängen in km in die Gleichung 

einsetzen, wenn man die Längen-Matrizen mit ψ -1 multipliziert. 

⎛ 

⎜ 

⎜ 

⎜ 

⎝− 

⎛ 1 1 

⎜ + 

⎜ l1l 

l13 

⎜ 

⎜ 0 

⎜ 

⎜ 1 

⎜ 

− 

⎝ l 21 

0 

1 1 

+ 

l 2l 

l 23 

1 

− 

l 32 

1 ⎞ 

⎛ 1 ⎞ 

− ⎟ 

⎜ ⎟ 

l13 

⎟ ⎛U 

⎞ ⎜ l1l 

⎟ 

1 

⎛ P1 

⎞ 

1 ⎟ 1 ⎜ ⎟ ⎜ 1 ⎟ 1 1 ⎜ ⎟ 

− ⎟ ⋅ ⋅ ⎜U 

2 ⎟ = ⎜ ⎟ ⋅ ⋅U 

I − ⋅ ⎜P2 

⎟ 

l 23 ⎟ ψ ⎜ ⎟ ⎜ l 2l 

⎟ ψ U n ⎜ ⎟ 

1 1 1 ⎟ ⎝U 

3 ⎠ ⎜ 1 ⎟ 

⎝P3 

⎠ 

+ + 

l 

⎟ 

⎜ ⎟ 

31 l 3I 

l 32 ⎠ 

⎝ l 3l 

⎠ 

⎛ 1 1 

⎜ + 

⎜ 205 205 

⎜ 0 

⎜ 

⎜ 1 

⎜ − 

⎝ 205 

0 

1 1 

+ 

225 100 

1 

− 

100 

1 ⎞ ⎛ 1 ⎞ 

− ⎟ ⎜ ⎟ 

205 ⎟ ⎛U 

⎞ ⎜ 205 

1 ⎟ 

⎛ P1 

⎞ 

1 ⎟ 1 ⎜ ⎟ 

⎜ 1 ⎟ 1 ψ ⎜ ⎟ 

− 

⋅ ⎜U 

2 ⎟ = ⋅U 

I − ⋅ 

⎟ ⎜ ⎟ 

⎜P2 

⎟ 

100 m 

⎟ 

⎜ ⎟ 225 m U n 

⎜ ⎟ 

⎜ ⎟ 

1 1 1 ⎝U 

3 ⎠ 1 

⎝P3 

⎠ 

+ + ⎟ ⎜ ⎟ 

205 300 100 ⎠ ⎝ 300 ⎠ 

0, 

00976 

0 

0, 

00488 

⎛ 

⎜ 

⎜ 

⎜ 

⎝− 

0 

0 

0, 

01444 

− 

0, 

00976 

0, 

00488 

0, 

01 

0 

0, 

01444 

− 

− 0, 

00488 

− 0, 

01 

0, 

01821 

0, 

01 

⎞ ⎛U 

1 ⎞ ⎛0, 

00488⎞ 

⎛100 

⎞ 

⎟ 1 ⎜ ⎟ ⎜ ⎟ 1 

0, 

22Ω 

⎜ ⎟ 

⎟ ⋅ ⎜U 

2 ⎟ = ⎜0, 

00444⎟ 

⋅ 400V 

− 

⋅ ⎜100 

⎟kW 

⎟ m ⎜ ⎟ ⎜ m 1km ⋅ 400V 

3 0, 

0033 ⎟ 

⎜200⎟ 

⎠ ⎝U 

⎠ ⎝ ⎠ 

⎝ ⎠ 

− 0, 

00488⎞ 

⎛U 

1 ⎞ ⎛1, 

952⎞ 

⎛0, 

055⎞ 

⎛1, 

897⎞ 

⎟ 1 ⎜ ⎟ ⎜ ⎟ V ⎜ ⎟ V ⎜ ⎟ V 

− 0, 

01 ⎟ ⋅ ⎜U 

2 ⎟ = ⎜1, 

776⎟ 

− ⎜0, 

055⎟ 

= ⎜1, 

721⎟ 

m 

m m m 

0, 

01821 ⎟ ⎜ ⎟ ⎜ 

3 1, 

332⎟ 

⎜0, 

110 ⎟ ⎜1, 

222⎟ 

⎠ ⎝U 

⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ 

Hieraus ergibt sich der Lösungsvektor für die Knotenpunktspannungen 

und den Spannungsfall in %: 

⎛U 

1 ⎞ ⎛384, 

44⎞ 

⎜ ⎟ ⎜ ⎟ 

⎜U 

2 ⎟ = ⎜382, 

44⎟V 

⎜ ⎟ ⎜ 

3 380, 

15 ⎟ 

⎝U 

⎠ ⎝ ⎠ 

Für den Lastfluss gilt: 

P 

I, 

1 

= P 

x, 

y 

= − 

⎛ ∆u1 

⎞ ⎛ − 3, 

89⎞ 

Uν 

− U 

⎜ ⎟ ⎜ ⎟ 

n 

oder mit ∆u 

= ⋅100% 

für ∆u in %: ⎜∆u 

2 ⎟ = ⎜− 

4, 

39⎟% 

U n 

⎜ ⎟ ⎜ 

3 4, 

96⎟ 

⎝∆u 

⎠ ⎝− 

⎠ 

Un 

400 

( U − U ) ⋅U 

⋅λ 

= − ( U − U ) ⋅ = −( 

400 − 384, 

44) 

= −138 

kW 

x 

y 

n 

x, 

y 

I 

1 

l 

I, 

1 

⋅ψ 

205 ⋅ 0, 

22 

(Anmerkung: vom Punkt x aus abfließende Last wird negativ gezählt, d.h. Ux > Uy) 

100 kW

42 

7.3.3 Anwendung der Lastflussberechnung nach dem Praktiker-Verfahren 

U I 

100 kW 

205 m 

300 m 

225 m 

111,00 kW 

30,77 kW 

225 m 

2 

100 m 

Damit ist der Lastfluss vollständig bestimmt. 

Die Knotenspannungen können nun mit der 

Gleichung: P − ( U − U ) ⋅U 

⋅λ 

⇒ ( U −U 

) 

x, 

y 

x, 

y = x y n x, 

y 

y x = berechnet werden. 

U n ⋅ λx, 

y 


1 

2 

205 m 

100 m 

100 kW 

Im ersten Schritt werden alle Zweiglasten Im zweiten Schritt werden alle Zweiglasten 

in die benachbarten Knotenpunkte verlagert in den Knotenpunkten zusammengefasst 

50 kW 

1 

1 

U I 

30,77 kW 

205 m 

300 m 

225 m 

2 

205 m 

100 m 

50 kW 

3 

69,23 kW 

200 kW 

Im dritten Schritt werden alle parallelen Leitungen 

zu einer Ersatzleitung zusammengefasst 

173,24 m 

U I 3 

30,77 kW 

325 m 

319,23 kW 

Im fünften Schritt werden alle Leistungen 

zurück verlagert. 

z.B. 208, 

23 ⋅173, 

24 

P 205 = 

= 87, 

98kW 

410 

1 

87,98 kW 

205 m 

205 m 

U I 

3 

300 m 

120,25 kW 

319,23 kW 

P 

3 

U I 

200 kW 

30,77 kW 

205 m 

300 m 

225 m 

2 

205 m 

100 m 

3 

319,23 kW 

Im vierten Schritt werden die Teilleistungen 

der beiden parallelen Zweige nach der 

Stromteilerregel berechnet und eingetragen. 

325 

P1 = P 

= 208, 

23kW 

325 + 173, 

24 

173,24 m 

U I 3 

30,77 kW 

208,23 kW 

111,00 kW 

325 m 

319,23 kW 

Im sechsten Schritt werden alle vorher verlagerten 

Leistungen addiert und eingetragen 

100 kW 

1 

137,98 kW 

37,98 kW 

205 m 

U I 

205 m 3 

300 m 

141,77 kW 

120,25 kW 

2 

225 m 

100 kW 

200 kW 

41,77 kW 

100 m

U I 

U I = 400,0 

V 


43 

Lastfluss und Spannungen in einem Modellnetz 

mit 3 Lastpunkten und einer Speisespannung 

Das negative Vorzeichen bei den Lastflüssen bedeutet: vom Bezugspunkt aus abfließende Leistung. 

Die Leitungslängen können hier direkt in km eingegeben werden (Diese werden nach Tabelle 1 übertragen). 

-400,0 

U1= 384,44 kV 

100 kVA 

-138,0 

-38,0 

205 m 205 m 

-120,2 

300 m U3= 380,16 V 

200 kVA 

-141,8 

225 m 

Uebung zur Vorlesung EV/EW 

Prof. Dr.-Ing. Helmut Alt, FH Aachen 

U I = 20,0 

kV 


2 

S2 

1 

S1 

U2= 382,46 V 

100 kVA 

-41,8 

100 m 

Lastflussrechnungen werden in der Praxis mit umfangreichen Computerprogrammen unter Verwendung 

optimierter mathematischer Lösungsalgorithmen z.B. nach dem Newton-Raphson- 

Verfahren mit komplexen Datensätze durchgeführt. 

U I 


mit 3 Lastpunkten und 2 Speisespannungen 


Die Leitungslängen können hier direkt in km eingegeben werden (Diese werden nach Tabelle 1 übertragen). 

-9,01 

U1= 19,363 kV 

5,00 MVA 

-4,06 

-3,13 

-4,06 

10 km 6 km 10 km 

-4,95 

12 km 


1 

U2= 19,069 kV 

12,00 MVA 

3 

-3,96 

15 km 

-0,04 

-5,96 

5 km 10 km 

2 3 

S2 

S1 

S3 

U3= 19,065 kV 

6,00 MVA 

S3 

-13,99 

U II = 

U II 

20,0 

kV

44 

Bei Einspeisungen der Leistung aus Photvoltaikanlagen im Niederspannungsnetz wird das Spannungsniveau 

im Netz wesentlich durch die Sonneneinstrahlung beeinflußt. Bei wolkenlosem Himmel 

wird die Peakleistung eingespeist, bei trüber Wetterlage wird keine Leistung eingespeist, obschon 

der Leistungsbedarf aller Verbraucher dann sogar stark ansteigt. Dadurch variiert die Spannung 

in der Nähe der Einspeisestelle realtiv stark. 

U I = 


mit 3 Lastpunkten und Photovoltaikeinspeisung 


Die Leitungslängen können hier direkt in m eingegeben werden (Diese werden nach Tabelle 1 übertragen). 

Netz-Einspeisung 

U I 


U1= 383,75 

100 kVA 

V 

Solare-Einspeisespannung 

U II = 400,00 V 

bedeckt 

Sonne 

-466,4 kVA 

S3 

400,00 V -133,6 kVA 

300 m U3= 378,49 V 

15,1 kVA 300 kVA 

100 m 

-184,9 kVA 

225 m 



U I = 

S1 

-147,8 kVA -47,8 kVA 

205 m 205 m -133,6 kVA 

300 m 

S2 

1 

2 

U2= 377,68 

200 kVA 

V 

Im obigem Beispiel liefert die Photovoltaikanlage rund 120 kW Wirkleistung mit dem Leistungsfaktor 

cos φ =0,9 auch induktive Blindleistung, also eine Scheinleistung von 133,6 kVA. Dadurch 

wird die Spannung am Einspeisepunkt gegenüber dem Netzpunkt 3 von 378,5 V auf 400 V 

angehoben. 

Ziehen Regenwolken auf, so dass die Einspeisung verschwindet und durch 10,8 kVA Bezugsleisung 

ersetzt wird, sinkt die Spannung am Netzpunkt 3 auf 370 V und am Einspeisepunkt unvermeidbar 

auf 368 V ab. Bei Schwachlast mit 10 % der Nennlast und voller Sonne kehrt sich der 

Lastfluss am Speisetrafo um, es werden 61,7 kVA 

zurück gespeist und die Spannung 

U II steigt auf 424 V an (mit 56 V 

Spannungshub). 

Netz-Einspeisung 

U I 

3 

U1= 379,37 

100 kVA 

V 

~ 

U II 

Solare-Einspeisespannung 

U II = 368,00 V 

bedeckt 

Sonne 

-610,8 kVA 

S3 

400,00 V -188,1 kVA 

300 m U3= 369,73 V 

-35,1 kVA 300 kVA 

100 m 

-235,1 kVA 

225 m 



S1 

-187,6 kVA -87,6 kVA 

205 m 205 m 10,8 kVA 

300 m 

S2 

1 

2 

U2= 371,62 

200 kVA 

V 

3 

~ 

U II

45 

7.4 Spannungs-Leistungsdiagramme 

7.4.1 Spannungs- und Leistungsverhältnisse bei Gleichstrom 

2 

I 

U0 

P = U ⋅ I , I = , 

U 

P = , 

U 0 

P = U ⋅ 

Ri 

+ R R Ri 

+ R 

2 

Ri 

⇒ U ⋅ U0 

= P ⋅ Ri 

+ P ⋅ R = P ⋅ Ri 

+ U 

U0 = 

P U R 

2 

U − U ⋅U 

0 + P ⋅ Ri 

= 0 ⇒ U = f (P) 

U 0 ⎛U 

0 ⎞ 

U1, 2 = ± ⎜ ⎟ − P ⋅ R 

2 ⎝ 2 ⎠ 

Z = R+jX I 

Netz A Netz B 

UA, δA 

2 

∆U 

p v 

S / 

= ⋅ R ⋅ l`⋅10 

2 

U 


i 

folgt mit: 

P 

p = 

Pk 

, Pk 

2 

U0, 

n 

= : u1, 2 

Ri 

u0 

= ± 

2 

2 

⎛ u0 

⎞ 

⎜ ⎟ − p 

⎝ 2 ⎠ 

U 0 

u0 

U 

= 1 

1 

, p max = ⇒ Pmax 

= P bei u0 = 1 

k 

4 

4 

0n 

Der zulässige Betriebsbereich ist in dem 

Diagramm für 10 % Spannungsabweichung 

vom Nennwert der Spannung gekennzeichnet. 

Der Maximalwert der Leistungsabgabe beträgt 

bei Nennspannung 1/4 der Kurzschlussleistung 

Pk. Bei höherer Leerlaufspannung 

verschiebt sich der Punkt für die maximale 

Leistungsabgabe zu höheren Werten der 

Leistung und Spannung. 

Der Wirkungsgrad der Übertragung mit maximaler 

Leistung ist nur 50%, da Ri=R ist. 

7.4.2 Spannungs- und Leistungsverhältnisse 

bei Wechselstrom/Drehstrom 

Energiefortleitung im Übertragungsnetz 

mit Normierung der Spannung U auf die Nennspannung U0n 

Spannung / Nennspannung u 

UB, δB 

4 

2 

1 ⎛ 1⎞ 

und für u0 = 1: u1, 2 = ± ⎜ ⎟ − p 

%/100km 

2 

⎝ 2 ⎠ 

U A = U B + ∆U 

, 

∆U 

= jX ⋅ I 

Näherungsweise gilt in 

Hochspannungsnetzen: 

Z ≅ jX , b I jX U ⋅ ≅ ∆ 

Für die Verlustleistung 

2 

gilt: Pv = 3 ⋅I 

⋅R 

Pv 

2 

Für die spez. Verlustleistung pv 

= gilt mit Pv = 3 ⋅I 

⋅R 

und U als Leiterspannung sowie der 

S 

Übertragungsleistung S = 3 ⋅U 

⋅I 

: 

⎛ S ⎞ 

3 ⋅ ⎜ ⎟ ⋅ R′ 

⋅ l 

2 

3 ⋅ I ⋅ R`⋅l 

U 

S 

p 

⎝ 3 ⋅ ⎠ 

v = = 

= ⋅ R′ 

⋅ l 

2 

S 

S U 

Setzt man in diese Gleichung die Übertragungsleistung S in MVA, Die Leiterspannung U in kV, den 

längenbezogenen Leitungswiderstand R′ in Ω/km und die Leitungslänge l` in vielfache von 100 

km ein, so ergibt sich die zugeschnittene Zahlenwertgleichung: 

1,2 

1,0 

0,8 

0,6 

0,4 

0,2 

0,0 

2 

Spannungs- Leistungsdiagramm einer 

Spannungsquelle mit Innenwiderstand 

Leerlauf 

u0=1,0 u0=1,1 Maximalleistung 

u0 = 1,0 

Maximalleistung bei R=Ri 

Kurzschluss 

Spannungs- und Leistungsdiagramm einer 

Spannungsquelle mit Innenwiderstand Ri 

zulässiger 

Betriebsbereich 

u0 = 1,1 

0,0 0,1 0,2 0,3 0,4 

Leistungsabgabe / Kurzschlussleistung p 

Spannung in V 

100 

80 

60 

40 

20 

0 

R=90 Ohm 

P=Pmax=250W 

R=Ri=10 Ohm 

Spannung U 

0 2 4 6 Strom I 8in in A 10 

unendlich 40 15 Lastwiderstand R in Ohm 0 

250 

200 

150 

100 

50 

0 

Leistung in W

46 

Die charakteristischen Gleichungen für die Wirk- und Blindleistungsübertragung ergeben sich bei 

vernachlässigtem ohmschen Anteil der Leitung aus dem Zeigerdiagramm für Z = X zu: 

X I cos φ = UA sin δ = X Iw 

φ 

UA X I sin φ = UA cos δ - UB = X Ib 

δ 

UB 

Iw 

φ 


I 

Ib 

U A 

PB 

= 3 ⋅U 

B ⋅I 

⋅ cosϕ 

= 3 ⋅U 

B ⋅I 

w = 3 ⋅U 

B ⋅ ⋅ sinδ 

X 

PB 

U A ⋅U 

B = 3 ⋅ 

X 

⋅ sinδ 

(UA und UB sind Phasenwerte 

der Spannungen) 

d.h. Die Wirkleistungsübertragung von Punkt A nach Punkt B ist 

überwiegend vom Leitungswinkel δ der Spannungen δ = δA-δB 

abhängig. 

Für die Leiterspannungswerte von UA Und UB gilt entsprechend: 

UA 

⋅U 

B 

PB 

= ⋅ sinδ 

X 

Die Einspeiseleistung am jeweiligen Netzpunkt ist dem Leistungskoeffizienten k des 

Verbundnetzes und der bewirkten Freqenzänderung proportional: 

∆ P = k ⋅ ∆f 

k UCTE-Netz =16.000 bis 20.000 MW/Hz 

Die Blindleistungsübertragung ist dagegen überwiegend von der Spannungsdifferenz zwischen der 

Spannung am Leitungsanfang UA und der Spannung am Leitungsende UE abhängig. 

Q 

B 

= 3 ⋅U 

B 

⋅ I ⋅ sinϕ 

= 3 ⋅U 

B 

⋅ I 

2 

( U ⋅U 

⋅ cos U ) 

3 

QB = ⋅ A B δ − 

X 

B 

b 

= 3 ⋅U 

B 

U 

⋅ 

A 

⋅ cosδ 

− U 

X 

1 

2 

Für UA und UB als Leiterspannungen gilt: QB = ⋅ ( U A ⋅U 

B ⋅ cosδ 

− UB 

) 

X 

Die Lastflüsse bei Parallelleitungen verteilen sich umgekehrt proportional zu den 

Zweigimpedanzen. Eine Beeinflussung der Lastaufteilung ist durch Einbringung einer 

Zusatzspannung in einem Parallelzweig in Form eines Transformators mit Längs- Quer- oder 

Schrägregelung möglich. Bei Querregelung wird vornehmlich der Wirkleistungsfluss, bei 

Längsregelung der Blindleistungsfluss beeinflusst: 

I1 Z1 

Uz 

Z 2 U z 

Z 1 U z 

I 1 = I ⋅ − 

I 2 = I ⋅ + 

I 

Z + Z Z + Z 

Z + Z Z + Z 

I2 

Z2 

1 

2 

1 

2 

Bei der Parallelschaltung eines Kabels zu einer 

Freileitung ergibt sich das Problem ungünstiger 

Lastverteilung, da die Impedanzen sehr unterschiedlich 

sind. 

z.B. Es wird zu einer 110 kV Freileitung 95/15 Al/St mit 350 A Nennbelastbarkeit ein 110 kV-Kabel 

NA2XS2Y 3x1x150 mit 319 A Nennbelastbarkeit parallel geschaltet. Die Impedanzen sind: 

Freileitung: ZFreileitung = (0,30 + j0,395) Ω/km, Kabel: ZKabel = (0,206 + j0,126) Ω/km. 

Die Zusatzspannung sei gleich Null Uz = 0, dann ergeben sich folgende Teilströme: 

I 

Freileitung 

= I ⋅ 0, 

33 ⋅ e 

− j14, 

38° 

I 

Kabel 

= I ⋅ 0, 

68 ⋅ e 

Die stromtragfähigere Freileitung übernimmt nur noch 33 % der Last, das Kabel 68 %. Das Kabel 

saugt infolge der niedrigeren Impedanz der Freileitung den Strom weg! Die Einfügung einer 

Zusatzspannung scheidet aus technisch-wirtschaftlichen Gründen aus. 

B 

Falls UA, UB Leiterspannungen (verkettete 

Spannungswerte) sind, entfällt der Faktor 3. 

j 6, 

95° 

1 

2 

1 

2

47 

Bezieht man die Wirk- und Blindleistungen mit den Spannungen als Leiterspannungen auf 

U An ⋅U 

Bn 

die Kurzschlußleistung Sk 

= , so ergeben sich folgende normierte Gleichungen: 

X 

2 

U A U 

p B = u A ⋅u 

B ⋅ sinδ 

und qB = uA 

⋅ uB 

⋅ cosδ − uB 

mit: u = , u = 

1 

1 

2 

sinδ = ⋅ pB 

, cos = ( qB 

+ uB 

) 

u ⋅u 

u ⋅u 

Spannung / Nennspannung uB 

1,4 

1,2 

1,0 

0,8 

0,6 

0,4 

0,2 

0,0 

A 

B 

u + 

Spannungs- Leistungsdiagramm einer 

Übertragungsleitung 

tan phi =0 tan phi =1 tan phi = -1 pB max 

Leerlauf 

Kurzschluss 

zulässiger 

Betriebsbereich 

0,0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 

Wirkleistung / Kurzschlussleistung pB 


A 

B 

kapazitive Last phi = -45° 

rein ohmsche Last phi = 0° 

induktive Last phi = 45° 

A 

Un 

B 

B 

Un 

2 

[ B B ] 

1 2 

2 

δ daraus folgt: = p + ( q + u ) 

2 2 2 2 

2 4 

4 2 

2 2 2 

A ⋅ uB 

= p B + qB 

+ 2qB ⋅u 

B uB 

u B + u B ( 2q 

B − u A ) + pB 

+ q B = 0 

2 

2 2 2 

x + x( 

2qB 

− u A ) + pB 

+ qB 

= 0 

2 

2 

u ⎛ 

A u ⎞ 

A 

2 2 

x1, 2 = − qB 

± ⎜ q ⎟ B − qB 

− pB 

2 ⎜ 

− 

mit 

2 ⎟ 

⎝ ⎠ 

2 

2 

2 

u 

⎛ 

A 

u ⎞ A 

x p ⎜ ⎟ 

1 , 2 = − B tanϕ 

± − pB 

A tanϕ 

+ 

2 

⎜ ⎟ 

⎝ 2 ⎠ 

2 

2 ( u p ) 

2 

2 

2 

u 

⎛ 

A 

u ⎞ A 

u B = − p ⎜ ⎟ 

B tanϕ 

± − pB 

A tanϕ 

+ 

2 

⎜ ⎟ 

⎝ 2 ⎠ 

2 

2 

u ⎛ A u ⎞ A 

Für pB = 0 gilt: u B = ± 

⎜ 

⎟ = uA 

2 ⎝ 2 ⎠ 

2 

B 

2 ( u p ) 

q 

1 B 

u ⋅u 

B 

tan ϕ = folgt für: q B = pB 

⋅ tanϕ 

pB 

, 

B 

, Für tan ϕ = 0 gilt: 

2 

A 

2 

B 

2 

2 

u ⎛ A u ⎞ A 

uB = ± − p 

2 ⎜ 

2 ⎟ 

⎝ ⎠ 

2 

2 

B 

Bei rein ohmscher 

Last ist der 

Spannungsfall am 

geringsten. 

Bei induktiver Last 

ist der Spannungsfall 

groß. 

Bei kapazitiver Last 

steigt die Spannung 

am Lastpunkt an, es 

besteht die Gefahr 

der Überspannung. 

Der zulässige Betriebsbereich 

ist 

wesentlich kleiner 

als der mögliche 

Lastbereich zwischen 

Leerlauf und 

Kurzschluss bzw. 

bis zum Punkt maximalerLastentnahme 

(Radikant 

der inneren Wurzel 

größer Null, vergleiche 

Ra = Ri bei 

Gleichstrom). 

Auch hier ergibt sich ein Punkt maximaler Leistungsabgabe, der aber in der Energietechnik aus 

Gründen minimaler Leitungsverluste und vertretbarem Spannungsfall bei weitem nicht erreicht 

wird.

48 

8. Kurzschlussstromberechnung 

8.1 Ableitung der Allgemeinen Gleichung für den Kurzschlussstrom 

i(t) 

~ 

di 

u( t) 

= uˆ 

⋅ cos( 

ωt − ε ) , u( t) 

= i ⋅ R + L ⋅ ⇒ 

dt 

di uˆ 

i + T ⋅ = ⋅ cos ωt − ε 

dt R 

Dgl. 1.Ordnung ( ) 


40 

0 

-40 

ε 

u(t) 

0 5 10 15 20 

ωt 

ms 

u( 

t) 

di L ω ⋅ L X 

= i + T ⋅ mit: T = = = 

R dt R ω ⋅ R ω ⋅ R 

L 

, T = ist die Zeitkonstante des Systems 

R 

Homogene Gleichung: 

di h 

T 

i h + T ⋅ = 0 mit dem Lösungsansatz: i h = k ⋅ e 

dt 

Partikuläre Lösung durch Ansatz in Form des Störgliedes: 

= A ⋅ sinωt + B ⋅ cosωt 

i p 

di p 

= A ⋅ω 

⋅ cosωt − B ⋅ω 

⋅ sinωt 

mit L multipliziert und eingesetzt in die 

dt 

⋅L 

X 

Ausgangsdifferenzialgleichung 1. Ordnung ergibt mit T = = 

R R 

ω 

ω : 

di 

uˆ 

i + T ⋅ = ( A − B ⋅ωT 

) ⋅ sinωt + ( B + A ⋅ωT 

) cosωt 

= ⋅ ( cosωt 

⋅ cosε 

+ sinωt 

⋅ sinε 

) 

dt 

R 

Der Koeffizientenvergleich ergibt zwei Gleichungen zur Bestimmung der beiden unbekannten Grö- 

uˆ 

uˆ 

uˆ 

ßen A und B: A − B ⋅ ωT = ⋅ sinε 

, B ⋅ ωT + A = ⋅ cosε 

oder A + B ⋅ ωT = ⋅ cosε 

R 

R 

R 

Diese ergeben sich aus den Matrizengleichungen: 

( ) ( ) 2 

2 

A = 

uˆ 

⋅ sinε 

− ωT 

R 

uˆ 

⋅ cosε 

1 

R 

1 − ωT 

uˆ 

uˆ 

⋅ sinε 

+ ⋅ωT 

⋅ cosε 

R R 

uˆ 

sinε 

+ ωT 

⋅ cosε 

= 

= ⋅ 

1+ 

ωT 

R 1+ 

ωT 

ωT 

1 

uˆ 

sinε 

+ ωT 

⋅ cosε 

R R ⋅ sinε 

+ X ⋅ cosε 

⎛ R X ⎞ 

A = ⋅ 

⋅ = uˆ 

⋅ 

= uˆ 

⋅ ⎜ ⋅ sinε 

+ ⋅ cosε 

⎟ 

2 

2 2 

2 

2 

R 1+ 

( ωT 

) R R + X 

⎝ Z Z ⎠ 

uˆ 

⎛ R X ⎞ 

A = ⋅ ⎜ ⋅ sinε 

+ ⋅ cosε 

⎟ = iˆ 

⋅ ( cosϕ 

sinε 

+ sinϕ 

cosε 

) = iˆ 

sin( 

ε + ϕ) 

Z ⎝ Z Z ⎠ 

entsprechend folgt für B: 

uˆ 

⎛ R X ⎞ 

B = ⋅ ⎜ ⋅ cosε 

+ ⋅ sinε 

⎟ = iˆ 

⋅ ( cosϕ 

cosε 

+ sinϕ 

sinε 

) = iˆ 

cos( 

ε + ϕ) 

Z ⎝ Z Z ⎠ 

t = i t + i t mit der Anfangsbedingung: i ( t = 0 ) = 0 folgt: 

i h p 

Gesamte Lösung: () () () 

t 

R 

u(t) 

X 

ik(t) 

− 

T i() 

t = k ⋅ e 

− 

+ iˆ 

T 

[ sin( 

ε + ϕ ) ⋅ sinωt 

+ cos( 

ε + ϕ ) ⋅ cos ωt 

] = k ⋅ e + iˆ 

⋅ cos[ 

ωt 

− ( ε + ϕ ) ] 

Aus: 0 = + iˆ[ 

sin( 

ε + ϕ) 

⋅ 0 + cos( 

ε + ϕ) 

⋅1] 

= k + iˆ 

⋅ cos[ 

( ε + ϕ) 

] = −î 

⋅ cos ε + 

k folgt: k ( ϕ) 

folgt die 

⎪⎧ 

⎪⎩ 

− 

Gesamte Lösung: () = ˆ t 

i t i ⋅ ⎨cos[ 

ωt − ( ε + ϕ) 

] − e ⋅cos( 

ε + ϕ) 

⎬ 

⎪⎭ 

T 

t 

⎪⎫ 

t 

−

49 

8.2 Stosskurzschlussstrom und zeitlicher Verlauf des Kurzschlussstromes 

Der sich aus der allgemeinen Gleichung für den Kurzschlussstrom ergebende Maximalwert des 

Kurzschlussstromes nennt man Stosskurzschlussstrom Is. Diesen findet man, wenn die differnzierte 

Allgemeine Gleichung für den Kurzschlusstrom gleich Null gesetzt wird: 

T 

⎪⎧ 

− 

⎪⎫ 

Allgemeine Gleichung: () = ˆ t 


ωt − ( ε + ϕ) 

] − e ⋅ cos( 

ε + ϕ) 

⎬ Die einhüllende Grenzlinie 

⎪⎩ 

⎪⎭ 

erhält man, wenn man den cos-Funktionswert der eckigen Klammer gleich +/- 1 setzt. 

t 

di ⎪⎧ 

⎡ − 

⎤⎪⎫ 

= ˆ 1 T 

i ⋅ ⎨− 

ω sin[ 

ωt 

+ ( ε + ϕ) 

] − ⎢− 

⋅ e ⋅ cos( 

ε + ϕ) 

⎥⎬ 

=0, ⇒ 

dt ⎪⎩ 

⎢⎣ 

T 

⎥⎦ 

⎪⎭ 

sin 

1 

ωT 

− 

T 

[ ω t − ( ε + ϕ) 

] = ⋅ e ⋅ cos( 

ε + ϕ) 

FürR ≈ 0 gilt: sin ( ) = 


t 

− 

T 

sin[ 

ω t − ( ε + ϕ) 

] = ⋅ e ⋅ cos( 

ε + ϕ) 

X 

[ ωt − ε + ϕ ] 0 ⇒ [ ω − ( ε + ϕ) 

] = k ⋅ π 

R 

t 

t mit k = 0, 

1, 

2, 

3, 

L 

ω t = ε + ϕ , für R = 0 ist ϕ = −90° 

(induktiv) , ωt = ε − 90° 

1 

( ) [ ( ) ] ( ) ⎟ t 

t 

⎪⎧ 

− 

⎪⎫ 

⎛ − ⎞ 

= ˆ 

T 

⋅ ⎨ ε − ° + ε − ° − ⋅ ε − ° ⎬ = ˆ⎜ 

T 

i t1 

i cos 90 90 e cos 90 i 

⎜ 

1− 

e ⋅ sinε 

⎪⎩ 

⎪⎭ ⎝ 

⎠ 

Das Maximun wir für ε = −90° 

oder für ε = 270° 

jeweils am Nulldurchgang der Spannung! 

Für den Maximalwert des Stromes gilt somit: 

t ⎛ − ⎞ Uˆ 

T 

i( 

t ) iˆ 

1 = ⎜1 

e ⎟ 

⎜ 

+ 

⎟ 

≈ 1, 

8 ⋅ 

⎝ ⎠ Zk 

U ⋅ 2 

Für den Stosskurzschlussstrom IS gilt: IS 

= κ ⋅ 

Z k 

U ⋅ 2 

IS, 

max = 1, 

8 ⋅ 

Z k 

In der Praxis ist X k ≈ 10 ⋅ Rk 

. 

L X k 

Somit gilt für die Zeitkonstante T: T = = 

R ω ⋅ Rk 

10 ⋅ R 1 

= 

≈ s ≈ 30 ms 

1 10 ⋅π 

2 ⋅π 

⋅ 50 ⋅ R 

s 

Der Kurzschlusswechselstrom ´´ 

I k ist der sich zu Beginn des Kurzschlusses ergebende 

Wechselstromwert: 

´´ c ⋅U 

n 

I k = mit c = 1,1 

Z k 

kA 

50 

i(t) 

Kurzschlussstrom i(t) 

i(t) o.G. i(t) u.G. u(t) 

Beispiel: Un = 20 kV 

Sn = 60 MVA 

uk = 10% 

ε = 270° 

Xk = 0,66 Ω, φk = 84° 

Rk = 0,07Ω 

T = 30,3 ms 

Ik`` = 17,3 kA (für c = 1) 

Is = 42,3 kA 

Kurzschlussstrom 

25 

0 

-25 

-50 

0 20 40 60 Zeit 80in ms 

-40 

100 

In dem Diagramm ist die Generatorspannung für ε = 270° und der Kurzschlussstrom dargestellt. 

1 

kV 

40 

30 

20 

10 

0 

-10 

-20 

-30

50 

8.3 Kurzschlusswechselstrom und Kurzschlussleistung 

Aus der Allgemeine Gleichung für den Kurzschlussstrom: 

T 

⎪⎧ 

− 

⎪⎫ 

() = ˆ t 


ωt − ( ε + ϕ) 

] − e ⋅ cos( 

ε + ϕ) 

⎬ 

⎪⎩ 

⎪⎭ 

ergeben sich folgende für die Berechnung der dynamischen und thermischen Kurzschlussbeanspruchung 

der Betriebsmittel gemäß den VDE Bestimmungen (VDE 0102, 0103) relevanten Effektivwerte: 

Kappa = f(R/X) 

Anfangskurzschlusswechselstrom ´´ 

I K : 

I 

´´ 

K 

c ⋅U 

n 

= 

3 ⋅ Z 

, ( ) ( ) 2 

2 

k = ∑ Rk 

+ ∑ X k 

Z , 

k 

2 

1, 

1⋅ 

U n 

Für die Einspeisequelle gilt: ZQ 

= ´´ 

Sk 

, Q 

Mit X Q = 0 , 995 ⋅ ZQ 

, RQ = 0 , 1⋅ 

X Q , S´´k,Q = 35 GVA 

Der Kurzschlusswechselstrom ´´ 

I k ist der sich zu Beginn 

des Kurzschlusses ergebende Wechselstromwert: 

´´ c ⋅U 

n 

I k = mit c = 1,1 

Z k 

´´ 

Der Stosskurzschlussstrom beträgt: IS = κ ⋅ 2 ⋅ I k 

Für die Stossziffer κ gilt: κ = 1, 

022 


+ 

0, 

96899 

⋅ e 

m 

2,00 

1,50 

1,00 

0,50 

0,00 

R 

−3, 

0301⋅ 

X 

´´ 

´´ 

Die Kurzschlussleistung ergibt sich zu: Sk = 3 ⋅ I k ⋅U 

n 

Der thermisch wirksame Mittelwert des Kurzschlussstromes 

über die Zeit Tk ergibt sich zu: 

Tk 

1 2 

Ith 

= ⋅ ∫ i k () t ⋅ dt , I th = I k ⋅ m + n 

Tk 

0 

´´ 

, 

Der Faktor m kennzeichnet das 

abklingende Gleichstromglied, n das 

abklingende Wechselstromglied. Für 

generatorferne Kurzschlusspunkte ist der 

Faktor n = 1. 

Für m gilt die Näherung: 

2 

x 

− 

κ −0, 

6 

2 

κ 

m = ⋅ e , 

2 

Beispiel: 

x 

= 2 + lg 

T 

k 

1s 

Kurzschlussdaten auf der Unterspannungsseite 

einer 380/110 kV 

Transformator - Einspeisung mit 

350 MVA Nennleistung, 

uk = 17%, aus einem 380 kV 

Übertragungsnetz mit 35 GVA 

Kurzschlussleistung: 

Quellenhinweis 

Alt, H.: Kurzschlussstromberechnung 

mit dem programmierbaren 

Taschenrechner. Elektrizitätswirtschaft, 

Jg. 79(1980), Heft 10, 

S. 379-382. 

Kappa 

2,00 

1,80 

1,60 

1,40 

1,20 

0,0 0,1 0,2 0,3 R/X 0,4 0,5 

Für Transformatoren gilt: 

X T 

2 

uk 

U n 

= 0, 995 ⋅ ⋅ 

100% 

Sn, 

T 

, RT = 0 , 1⋅ 

XT 

Bei Leitungen gilt für die Umrechnung 

auf das Spannungsniveau Un: 

2 

⎛ U N ⎞ 

X , = X ⋅ ⎜ ⎟ , 

L N L RL 

, N 

⎝ U ⎠ 

2 

⎛ U N ⎞ 

= RL 

⋅ ⎜ ⎟ 

⎝ U ⎠ 

m - Faktor für Gleichstromglied 

Kappa = 1,90 1,70 1,40 1,10 

10 100 Tk in ms 1000 

Un in kV Sn in MVA uk in % Tk in s SQ in GVA 

110 350 17 0,1 35 

Kappa = 1,74 Xk = 6,226 Ohm 

m = 0,63 Rk = 0,623 Ohm 

Kurzschlussimpedanz: Zk = 6,257 Ohm 

Kurzschlusswechselstrom: Ik´´ 11,16 kA 

Stosskurzschlussstrom: IS = 27,44 kA 

Kurzschlussleistung: Sk´´ = 2.127 MVA 

Thermisch wirksamer K.-S.: Ith = 14,24 kA

51 

Die Kurzschlussberechnung läßt sich vorteilhaft auf einer Excel-Vorlage auf Basis eines Modellnetzes 

vornehmen. Die gelb und orange gekennzeichneten Eingabedaten sind festen Zellen zugeordnet 

und hierzu die entsprechenden Gleichungen hinterlegt. Die Ergebnisse erscheinen dann in 

den gün markierten Zellen. Durch Variation der Leitungsdaten lassen sich vielfältige Anwendungen 

mit dieser Excel-Vorlage realieren. Die Excel - Tabellenrechnung ist zu einem komfortablen Ersatz 

des programmierbaren Taschenrechners für ingenieurtechnische Anwendungen geworden. 

Die Kurzschlußleistung nimmt mit wachsender Impedanz ab, die Kurzschlussströme steigen mit 

niedrigerer Spannung an. 


Interaktive Kurzschlussdatenberechnung im Modellnetz 

X in Ω = 2,72 2,72 2,47 

R in Ω = 0,51 0,51 0,47 

S k´´= 35 GVA Z Q 

T k = 0,1 s I S = 131 kA X Q = 4,5156 

I k´´ = 53 kA R Q = 0,4516 

380 kV S k´´ = 35 GVA κ = 1,7377 

I th = 68 kA m = 0,63 

350 MVA 

17 % Z k 

I S = 27 kA X k = 6,2261 

110 kV I k´´ = 11 kA R k = 0,6226 

S k´´ = 2.127 MVA κ = 1,7377 

I th = 14 kA m = 0,63 

2,92 R 1,2P X 1,2P R P,3P X P,3P 

0,88 0,255 1,36 0,2396 1,1859 

30,634 120,003425 

7,462024404 

3,77 

Z k 1,45 Zk 

Xk = 0,01090275 IS = 23 kA Xk = 7,412 

0,0109595 

Rk = 0,00111388 Ik´´ = 9 kA Rk = 0,8622 

κ = 1,7330091 S k´´ = 1.784 MVA κ = 1,7031 

m = 0,62 I th = 12 kA m = 0,59 

30 MVA 

12 % Z k 

I S = 52 kA I S = 17 kA X k = 1,837 

I k´´ = 21 kA 20 kV I k´´ = 7 kA R k = 0,1877 

S k´´ = 15 MVA S k´´ = 238 MVA κ = 1,733 

I th = 21 kA I th = 9 kA m = 0,62 

400 V 0,15 

630 kVA 0,07 Z k 

4 % I S = 15 kA X k = 1,987 

I k´´ = 6 kA R k = 0,2577 

S k´´ = 220 MVA κ = 1,6761 

I th = 8 kA m = 0,55 

Quellenhinweis 

Alt, H.: Kurzschlussstromberechnung mit dem programmierbaren Taschenrechner. Elektrizitätswirtschaft, 

Jg. 79(1980), Heft 10, S. 379-382. 

4,5383 

6,2572 

7,462 

1,8466 

2,0037

52 

9. Energiewirtschaft 

9.1 Strompreisbildung an der Strombörse 

Die an der Strombörse zugelassenen Makler sammeln die Stromeinkauforder und die Stromangebotsorder 

in einem Auftragsbuch. Für diese Order wird in einem Clearingverfahren diejenige Kombination 

ermittelt, bei der der größte Börsenumsatz bei minimalem Überhang nicht bedienter Order 

entsteht. Das Verfahren möge anhand dem folgenden Beispiel erkennbar werden: 

An der Strombörse werden von einem Börsenmakler fünf Lose elektrischer Energie aus verschiedenen 

Kraftwerken über je 250 GWh zu Preisen zwischen 50 und 90 €/MWh angeboten. Auf der 

Käuferseite besteht Kaufinteresse in ebenfalls fünf Quoten von 1.250 GWh, wenn der Preis bei 50 

€/MWh liegt und abnehmend auf 250 GWh wenn der hohe Preis von 90 €/MWh zum Zuge kommt. 

Der Börsenmakler ordnet die Angebote nach aufsteigenden Preisen und ermittelt zu jedem Preis 

die ausführbare Menge und den sich ergebenden Überhang nicht bedienter Optionen. Der Auktionspreis 

ist derjenige, bei dem die größte Auftragsmenge ausgeführt werden kann und der geringste 

Überhang verbleibt. Dies ist im vorliegenden Beispiel bei dem Preis von 70 €/MWh für 750 

GWh bei 0 GWh Überhang der Fall. Der Umsatz beträgt dann: 

Umsatz = 750 GWh ⋅ 70 €/MWh = 52, 

5Mio. 

€ 

Sinkt das Kaufinteresse auf 250 GWh ab, weil z.B. viel EEG-Windstrom vorrangig im Netz aufgenommen 

werden muss, so verringert sich der Strombezugspreis von 70 auf 50 €/MWh. Dies wirkt 

sich jedoch 

wegen der festen 

EEG- 

Vergütung 

durch den 

Netzbetreiber 

von 90 €/MWh 

insgesamt 

nicht kostenentlastend 

aus. 


Stromhandel Auftragsbuch 

Kauf - Angebote Verkauf - Angebote 

Menge Summe Preis Preis Menge Summe 

GWh GWh €/MWh €/MWh GWh GWh 

250 250 90 50 250 250 

250 500 80 60 250 500 

250 750 70 70 250 750 

250 1000 60 80 250 1000 

250 1250 50 90 250 1250 

Preis 

Clearing- Verfahren zur Preisbildung 

Auktionspreis = Preis bei dem die größte Auftragsmenge 

ausgeführt wird und der geringste Überhang verbleibt 

Menge 

Kauf 

Menge 

Verkauf 

Ausführbare 

Menge 

Überhang Umsatz 

€/MWh GWh GWh GWh GWh Mio. € 

50 1250 250 250 1000 12,5 

60 1000 500 500 500 30 

70 750 750 750 0 52,5 

80 500 1000 500 500 40 

90 250 1250 250 1000 22,5 

Preis 

Menge 

Kauf 

Menge 

Verkauf 

Ausführbare 

Menge 

Überhang Umsatz 

€/MWh GWh GWh GWh GWh Mio. € 

50 250 250 250 0 12,5 

60 250 500 250 250 15 

70 250 750 250 500 17,5 

80 250 1000 250 750 20 

90 250 1250 250 1000 22,5

53 

Bei den Kauf-Angeboten wird das Angebot mit dem höchsten Preis die größte Wahrscheinlichkeit 

haben bedient zu werden. Ebenso wird bei den Verkaufsangeboten das Angebot mit den niedrigsten 

Preisen die höchste Wahrscheinlichkeit haben, bedient zu werden. 

In dem folgenden Beispiel liegen Kaufangebote von 50 GWh zu 100 €/MWh vor, bis hin zu 400 

GWh, wenn der Preis nur 30 €/MWh betragen sollte. Derjenige, der 100 €/MWh zu zahlen bereit 

ist, nimmt den Strom selbstverständlich auch gerne zu nur 30 €/MWh an, so dass bei diesem Preis 

der Umsatz 1.800 GWh wäre. Bei den Verkaufs-Angeboten ist die Tendenz umgekehrt, dort würde 

die gesamte 

Menge von 

2.600 GWh 

angeboten, 

wenn der Preis 

100 €/MWh 

wäre, bei 

30 €/MWh sind 

nur 500 GWh 

verfügbar, da 

die teurer produzierenden 

Kraftwerke 

nicht eingesetzt 

werden. 

Der Börsenmakler ordnet 

die Angebote nach 

aufsteigenden Preisen 

und ermittelt die zu jedem 

Preis ausführbare 

Menge und den sich 

ergebenden Überhang 

nicht bedienter Optionen. 

Der Auktionspreis 

ist derjenige, bei dem 

die größte Auftragsmenge 

ausgeführt werden 

kann und der geringste 

Überhang verbleibt. 

Dies ist im vorliegenden 

Beispiel bei 

dem Preis von 50 

€/MWh für 1.050 GWh 

Stromhandel Auftragsbuch 

Kauf - Angebote Verkauf - Angebote 

Menge Summe Preis Preis Menge Summe 

GWh GWh €/MWh €/MWh GWh GWh 

50 50 100 30 500 500 

100 150 90 40 450 950 

150 300 80 50 400 1.350 

200 500 70 60 350 1.700 

250 750 60 70 300 2.000 

300 1.050 50 80 250 2.250 

350 1.400 40 90 200 2.450 

400 1.800 30 100 150 2.600 

Clearing- Verfahren zur Preisbildung 

Auktionspreis = Preis bei dem die größte Auftragsmenge 

ausgeführt wird und der geringste Überhang verbleibt 

Preis 

Menge 

Kauf 

Menge 

Verkauf 


Ausführbare 

Menge 

Überhang 

€/MWh GWh GWh GWh GWh 

30 1.800 500 500 1.300 

40 1.400 950 950 450 

50 1.050 1.350 1.050 300 

60 750 1.700 750 950 

70 500 2.000 500 1.500 

80 300 2.250 300 1.950 

90 150 2.450 150 2.300 

100 

bei 300 GWh Überhang der Fall. 

50 2.600 50 2.550 

Der Umsatz beträgt dann: Umsatz = 1. 

050 GWh ⋅ 50 €/MWh = 52, 

5Mio. 

€ 

Bisherige Spotmarktpreise liegen zwischen dem negativen Wert von -102 €/MWh am 22.12.2008 

in den frühen Morgenstunden und 1.720 €/MWh am 7. Januar 2003 am Abend von 19 bis 20 Uhr. 

Am 22.12.2008 ergab sich am Spotmarkt der EEX Leipzig ein neuer Rekord bei den negativen 

Handelspreisen. In der Zeit von 0 Uhr bis 6 Uhr bekam man für die folgenden Handelsmengen 

noch Geld dazu: 

Zeit Preis Handelsmenge 

h €/MWh MWh 

20.000 

Windleistungseinspeisung vom 17.12. bis 30.12.2008 

Installierte Leistung: 23.312 MW, zeitgleiche 

Summenleistung aller 19.868 Anlagen 

0-1: -9,98 14.912 

15.000 

Während dieser Zeitspanne am 

1-2: -29,59 15.714 

22.12.08 von 0 bis 6 Uhr wurde der 

Strom verschenkt und noch Geld in 

2-3: -101,52 15.645 

3-4: -101,52 15.575 

10.000 

Höhe von 5,53 Mio.€ dazu. 

4-5: -100,50 15.664 

5-6: -9,98 15.755 Die Vergütung dafür 

5.000 

Summe: 93.265 betrug rd.90 €/MWh 

Umsatz: -5,53 Mio. € 8,4 Mrd. € 


0 

17.12 19.12 21.12 23.12 25.12 27.12 29.12 

Tage im Dezember 2008 (Stunden-Mittelwerte)

EUR/MWh 

400 

Strompreis 

300 

200 

100 

0 

Dauerlinie und Ganglinie der Day - ahead 

Strompreise an der Leipziger Strombörse vom 

1.1. bis 8.1.2003 

Bis zu 1.719,72 EUR/MWh 

1 25 49 73 97 121 145 169 

Stundenkontrakte 

Preis 

in €/MWh 


54 

Handelsmenge 

MWh 

25.000 

20.000 

15.000 

10.000 

5.000 

0 

EEX Leipzig European Energy Exchange 

am Montag 22.12.2008 

Handelsvolumen: 

+17,24 Mio. € 

- 5,53 Mio. € 

A 8 

Handelsmenge Preis 

1 6 11 16 21 

Zeit 

Angebotsmenge 

A 1 = Menge aus thermischen Kraftwerken 

deren kurzfristiges runterfahren hohe Zusatzkosten verursacht! 

€/MWh 

-40 

-80 

-120 

Durchschnittspreis: p Ø,EEX = 22,70 EUR/MWh 

Im Sinne der gesetzlich vorgeschriebenen Transparenz der Börsenhandelsgeschäfte wurde eine 

zentrale neutrale Plattform für Energiemarktdaten „Transparency in Energy Markets“ eingerichtet, 

durch die gesetzliche Veröffentlichungspflichten erfüllt sowie freiwillige Selbstverpflichtungen 

der Marktteilnehmer umgesetzt werden. Diese Transparenzplattform für Erzeugungs- und 

Verbrauchsdaten (www.transparency.eex.com ) wurde durch die EEX zusammen mit den vier 

deutschen Übertragungsnetzbetreibern: 50Hertz Transmission GmbH, Amprion GmbH, EnBW 

Transportnetze AG und TenneT TSO GmbH in intensiver Zusammenarbeit mit den Verbänden 

BDEW, VKU, VIK und der Bundesnetzagentur sowie dem Bundesministerium für Wirtschaft und 

Technologie ins Leben gerufen. 

Die EEX ist verantwortlich für den Betrieb, welcher neben der Betreuung von Meldern und Nutzern 

die Plausibilisierung, Anonymisierung, Aggregierung sowie Veröffentlichung der gemeldeten Daten 

umfasst. 

0 

Meritorder-Preis den 

alle Anbieter erhalten 

Preis bei verminderter Nachfrage 

oder bei unkalkuliert höherer 

Windeinspeisung 

A 5 

A 4 

A 2 A 3 

A 1 

A 6 

A 7 

Nachfragekennlinie 

Angebotsmenge prinzipiell 

aus Kraftwerksart: 

A1: Laufwasser und Teilmengen 

thermische (must run) 

A2: Wasser, Wind und Sonne 

A3: Wasserkraftwerke 

A4: Kernkraftwerke 

A5: Braunkohlekraftwerke, neue 

A6: Braunkohlekraftwerke, ältere 

A7 Steinkohlekraftwerke 

A8: Erdgaskraftwerke 

Am Spotmarkt sinkt der Preis des Öfteren auf Null ab, am 5. 10. und 22.12. 2008 war er in den 

Morgenstunden aufgrund hoher nicht zeitgerecht kalkulierter Windstromeinspeisung sogar negativ. 

Wenn EEG-Strom aus Sonnen- Wind- oder Kleinwasserkraftanlagen ins Netz eingespeist wird, 

muss dieser vorrangig verbraucht werden. Dadurch verringert sich die Nachfrage und es ergibt 

sich ein neuer, geringerer Strompreis an der Börse. Dieser Effekt führt natürlich nicht zu nachhaltig 

niedrigeren Stromerzeugungskosten. Da diese Stromeinspeisungen ja entsprechend der EEG- 

Vergütung unabhängig von der Bedarfslage bereits vergütet wurden und inzwischen eine von den 

Strombeziehern zu erbringende Subventionshöhe von jährlich rd. 14 Mrd. € vorweg verursachen. 

Der preisreduzierende Merit-Ordereffekt verringert nicht die Stromerzeugungskosten insgesamt 

aufgrund von Windstromeinspeisungen, sondern optimiert ein wenig die Brennstoffkosten. 

80 

40 

0 

Preis

55 

9.2 Versorgungsqualität und Kenngrößen zur Versorgungszuverlässigkeit 

SAIFI (System Average Interruption Frequency Index) 

Dieser Index gibt die mittlere Häufigkeit von Versorgungsunterbrechungen pro angeschlossenen 

Kunden im Betrachtungszeitraum an: 

Summe aller Kundenunterbrechungen 

SAIFI = 

Summe aller versorgten Kunden 

Als Ergebnis erhält man die Häufigkeit, wie oft ein Kunde z.B. innerhalb eines Jahres unterbrochen 

wurde. 

SAIDI (System Average Interruption Duration Index) 

Dieser Index gibt die mittlere Dauer von Versorgungsunterbrechungen pro angeschlossenen Kun- 

den im Betrachtungszeitraum an: 

Kumulierte Dauer aller Kundenunterbrechungen 

SAIDI = 

Summe aller versorgten Kunden 

Als Ergebnis erhält man die durchschnittliche Unterbrechungsdauer eines Kunden z.B. innerhalb 

eines Jahres im Gebiet des Netzbetreibers. 

CAIDI (Cutomer Average Interruption Duration Index) 

Mit diesem Index wird die mittlere Unterbrechungsdauer eines unterbrochenen Kunden gemessen. 

CAIDI berechnet sich durch die Division von SAIDI und SAIFI: 

Kumulierte Dauer aller Kundenunterbrechungen 

SAIDI 

CAIDI = 

= 

Summe aller Kundenunterbrechungen 

SAIFI 

Als Ergebnis erhält man die durchschnittliche Unterbrechungsdauer aller von der Störung betroffenen 

Kunden im Netzgebiet des Netzbetreibers. 

Die Spannungsqualität ist in der Europanorm EN 50160 geregelt. Quelle: VDN 

Beispiel zur Messung der Versorgungszuverlässigkeit: 

Im ungestörten Betriebszustand versorgt ein Netzbetreiber insgesamt 100.000 Kunden. 

Innerhalb eines Jahres ereignen sich zwei Störungen mit gebietsweisen Unterbrechungen: 

1. Störung mit 65 Minuten Spannungsausfall für 1.000 Kunden 

2. Störung mit 45 Minuten Spannungsausfall für 3.000 Kunden 

SAIFI (System Average Interruption Frequency Index) 

1. 

000 + 3. 

000 1 

SAIFI = 

= 

100. 

000 a 

0, 

04 

Im Mittel ist ein Kunde 0,04 mal pro Jahr spannungslos, d.h. einmal in 25 Jahren. 


1 

a

56 

SAIDI (System Average Interruption Duration Index) 

1. 

000 ⋅ 65 + 3. 

000 ⋅ 45 min 

SAIDI = 

100. 

000 a 


= 

2, 

0 

min 

a 

Ein beliebiger Kunde ist im Mittel 2 Minuten pro Jahr spannungslos. 

CAIDI (Customer Average Interruption Duration Index) 

1. 

000 ⋅ 65 + 3. 

000 ⋅ 45 

CAIDI = 

min 

4. 

000 

= 

50, 

0 

min 

Erfährt ein Kunde eine Störung, so dauert diese im Mittel 50 Minuten. 

Nichtverfügbarkeit 1999 bis 2004 durch stochastische Versorgungsunterbrechungen: 

Mittlere kundenbezogene Unterbrechungshäufigkeit durch stochastische Versorgungsunterbrechungen

Bundeskanzlerin Frau Dr. Merkel bei ihrer Lernreise 2010 im Kernkraftwerk (KKW) Lingen: 

KKW Lingen 

Berliner Zeitung 

vom 27.8.2010 

Die jungen Leute können das, 

unser Umweltminister Norbert 

Röttgen muss es noch lernen. 

Aha, hier gibt’s Strom, auch 

wenn die Sonne nicht scheint 

und der Wind nicht weht, und 

noch 2,3 Mrd. € extra! 

„und sichere, gut bezahlte 

Arbeit ohne Verlagerungsgefahr 

nach China“ 

Steinkohle 

109,0 TWh (18,3 %) 

Braunkohle 

146,5 TWh (24,5 %) 

Jahresganglinie der Stromerzeugung des 

Kernkraftwerkes Isar 2: 

Kernenergie 

134,9 TWh (22,6 %) 


57 

Erdgas 

77,0 TWh (12,9 %) 

Bruttostromerzeugung 

596,8 TWh 

Monatsganglinie der Stromerzeugung des 

offshore Windparks Alpha Ventus im Monat Dezember 2010: 


80 

60 

40 

20 

0 

Brutto - Stromerzeugungsmix 2009 

Mineralölprodukte 

12,5 TWh (2,1 %) 

sonstige 

23,9 TWh (4,0 %) 

regenerative 

Stromerzeugung 

93,0 TWh (15,6 %) 

16 % vom Brutto- 

Stromverbrauch 

583 TWh 

Wasser 

19,0 TWh (3,2 %) 

Wind 

37,8 TWh (6,3 %) 

Biomasse 

25,0 TWh (4,2 %) 

Müll regenerativ 

5,0 TWh (0,8 %) 

Photovoltaik 

6,2 TWh (1,0 %) 

Brenn-elementewechsel mit 21. Revision 

Netzeinspeisung KKW ISAR 2 KKI 2009 

(Platz 2 der Top Ten Internationale Liste) 

Offshore-Windleistung im vorvormals E.on, nun 

Tennet - Netz im Monat Dezember vom 1.- 31.12. 2010 

1 5 9 13 17 21 25 29 

Zeit (Tage der 1/4 h - Leistungswerte) 

Da das zeitliche Windleistungsangebot an verschiedenen Standorten im deutschen Nordseegebiet 

naturgemäß zeitlich kaum unterschiedlich sein kann, wird die Verfügbarkeit der Leistung auch bei 

beliebiger Steigerung der Anzahl Windräder nicht besser, nur der Ordnatenmaßstab ändert sich 

dann zu höherer Leistung.

Vorlesungsmanuskript ET-EW 2011.pdf - von Prof. Dr.-Ing. H. Alt, FH ...

Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.

Template löschen?

Als Template speichern?