Underpinnings of fire management for biodiversity conservation in ...

Underpinnings of fire management for biodiversity conservation in reserves
Fire and adaptive management
Probability of ignition
8
Text Box 1.1. Spot fires
Spot fires are spawned from a parent fire, especially when its intensity is high. Two forms of spot-fire
phenomena are usually distinguished – short-distance spotting and long-distance spotting. Longdistance
spot fires may occur up to 30 km from the fire front (Luke and McArthur 1978, p. 102), are
usually completely isolated from the fire front, and occur singly or in small groups. They arise from
burning materials carried aloft in a convection column, but eventually escaping from it and falling onto
an ignitable fuel that is then set alight. The materials causing these spot fires can be called burning
brands or fire brands (Gould et al. 2007, p. 117) – ignitable materials of sufficient mass to carry the
distance without burning themselves out. Fire brands may originate from a variety of species, have
different compositions (e.g. bark, capsule), be glowing or flaming and large or small.
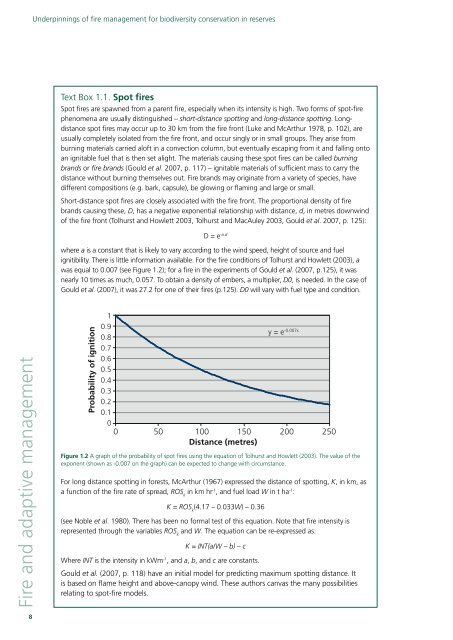
Short-distance spot fires are closely associated with the fire front. The proportional density of fire
brands causing these, D, has a negative exponential relationship with distance, d, in metres downwind
of the fire front (Tolhurst and Howlett 2003, Tolhurst and MacAuley 2003, Gould et al. 2007, p. 125):
D = e -a.d
where a is a constant that is likely to vary according to the wind speed, height of source and fuel
ignitibility. There is little information available. For the fire conditions of Tolhurst and Howlett (2003), a
was equal to 0.007 (see Figure 1.2); for a fire in the experiments of Gould et al. (2007, p.125), it was
nearly 10 times as much, 0.057. To obtain a density of embers, a multiplier, D0, is needed. In the case of
Gould et al. (2007), it was 27.2 for one of their fires (p.125). D0 will vary with fuel type and condition.
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0 50 100 150 200 250
Distance (metres)
Figure 1.2 A graph of the probability of spot fires using the equation of Tolhurst and Howlett (2003). The value of the
exponent (shown as -0.007 on the graph) can be expected to change with circumstance.
For long distance spotting in forests, McArthur (1967) expressed the distance of spotting, K, in km, as
a function of the fire rate of spread, ROS k in km hr -1 , and fuel load W in t ha -1 :
K = ROS k (4.17 – 0.033W) – 0.36
(see Noble et al. 1980). There has been no formal test of this equation. Note that fire intensity is
represented through the variables ROS k and W. The equation can be re-expressed as:
K = INT(a/W – b) – c
Where INT is the intensity in kWm -1 , and a, b, and c are constants.
y = e -0.007x
Gould et al. (2007, p. 118) have an initial model for predicting maximum spotting distance. It
is based on flame height and above-canopy wind. These authors canvas the many possibilities
relating to spot-fire models.