Quantum Information Theory with Gaussian Systems

More documents

Recommendations

Info

3 Optimal cloners for coherent states Replacing t(ξ) in (3.27) and letting ξi = (q, p), the i-th single-copy fidelity for the fixed input state |0〉〈0| is fi = tr[ρT Fi], where dq dp Fi = χin(q, p) 2π 2 exp i (p Pi − q i=j Qj) = exp −P 2 i /2 − i=j Q2 j /2 . (3.28) In the following, we study the weighted single-copy fidelities i λi fi by numerical computation and analytical arguments. For simplicity, we restrict this discussion to the case of 1-to-2 cloning. While in principle the method can be generalized, numerical computations of the fidelities might get more involved. The operator F for the weighted single-copy fidelity λf1(T) + (1 − λ)f2(T) = tr[ρT F] is composed of the weighted sum of the respective Fi: F = λ1 e −(Q2 2 +P2 1 )/2 + λ2 e −(Q2 1 +P2 2 )/2 (3.29a) ≃ λ1 e −(Q2 1 +Q2 2 )/2 + λ2 e −(P2 1 +P2 2 )/2 , (3.29b) where the second expression is obtained by applying an orthogonal, symplectic transformation such that Q1 ↦→ −P1 and P1 ↦→ Q1. Both forms are equivalent for the purpose of computing eigenvalues. The largest eigenvalue of F gives the maximal singlecopy fidelity, the corresponding eigenvector describes the optimal cloner. Before we detail their approximate computation, we discuss the results depicted in Fig. 3.2. Since a linear combination of Gaussian operators as in (3.29b) does in general not have Gaussian eigenfunctions, the optimal cloners are not Gaussian. In fact, comparing the optimal symmetric cloner yielding f1 = f2 ≈ 0.6826 with the best Gaussian cloner (see [53,54,55] and below), limited to f1 = f2 = 2 3 , already indicates the enhancement in fidelity by non-Gaussian cloners. A more detailed study of the best Gaussian 1-to-2 cloners (see below) results in the dotted curve of fidelity pairs in Fig. 3.2. Clearly, the non-Gaussian cloners perform better for every region of the diagram. The two symmetric cloners can be found at the intersection of the dashdotted diagonal with the dotted curve of best Gaussian cloners and the solid curve of optimal cloners. At the points of the singular cloners with f1, f2 = 1, the solid curve of optimal cloners has a nonfinite slope s = ∞ and s = 0, respectively, while the dotted curve of the best Gaussian cloners has a finite slope (see in particular (b) in Fig. 3.2). By the arguments of Section 3.2, this implies that the optimal cloners for f1 = 1, f2 = 1 do not coincide with the singular cloners. In contrast, the best Gaussian cloners for f1 ≈ 1 and f2 ≈ 1 are determined by the respective singular cloners; see also below. The trivialcopy-throughcloners, which yield fidelity f1 = 1 or f2 = 1, are singular in any case by Corollary 3.3. The following subsection gives details on the approximate, numerical computation of the largest eigenvalue of F and the corresponding eigenfunctions. To complement the results on optimal cloners, the last two subsections briefly investigate the best Gaussian cloner for 1-to-2 cloning with arbitrary weights and for symmetric 1-to-n cloning. Before this, we summarize the results in 48
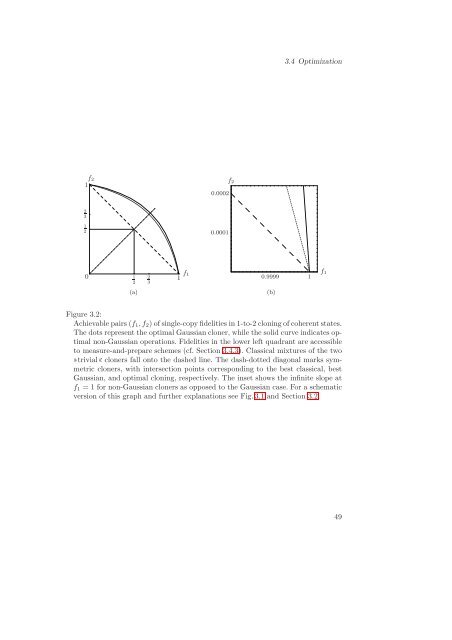
1 2 3 1 2 0 f2 1 2 (a) 2 3 1 f1 0.0002 0.0001 f2 0.9999 3.4 Optimization Figure 3.2: Achievable pairs (f1, f2) of single-copy fidelities in 1-to-2 cloning of coherent states. The dots represent the optimal Gaussian cloner, while the solid curve indicates optimal non-Gaussian operations. Fidelities in the lower left quadrant are accessible to measure-and-prepare schemes (cf. Section 3.4.3). Classical mixtures of the two trivialcloners fall onto the dashed line. The dash-dotted diagonal marks symmetric cloners, with intersection points corresponding to the best classical, best Gaussian, and optimal cloning, respectively. The inset shows the infinite slope at f1 = 1 for non-Gaussian cloners as opposed to the Gaussian case. For a schematic version of this graph and further explanations see Fig. 3.1 and Section 3.2. (b) 1 f1 49
Page 1 and 2:
Quantum Information Theory with Gau
Page 3:
Vorveröffentlichungen der Disserta
Page 6 and 7:
Contents Quantum Cellular Automata
Page 8 and 9: List of Figures viii
Page 10 and 11: List of Theorems x
Page 12 and 13: Summary mum is reached by a measure
Page 14 and 15: Summary 4
Page 16 and 17: 1 Introduction electromagnetic fiel
Page 18 and 19: 1 Introduction 8
Page 20 and 21: 2 Basics of Gaussian systems Since
Page 22 and 23: 2 Basics of Gaussian systems Theore
Page 24 and 25: 2 Basics of Gaussian systems For a
Page 26 and 27: 2 Basics of Gaussian systems for co
Page 28 and 29: 2 Basics of Gaussian systems 2.2 Ga
Page 30 and 31: 2 Basics of Gaussian systems As pur
Page 32 and 33: 2 Basics of Gaussian systems unitar
Page 34 and 35: 2 Basics of Gaussian systems In pha
Page 36 and 37: 2 Basics of Gaussian systems Remark
Page 38 and 39: 2 Basics of Gaussian systems 28
Page 41 and 42: 3 Optimal cloners for coherent stat
Page 43 and 44: 3.1 Setup 3.1 Setup A deterministic
Page 45 and 46: f2(T) 1 0 (a) 1 f1(T) f2(T) 1 0 (
Page 47 and 48: the expectation value of an arbitra
Page 49 and 50: 3.3 Covariance clone). A more gener
Page 51 and 52: 3.3 Covariance In the case of joint
Page 53 and 54: 3.3 Covariance where the second ide
Page 55 and 56: 3.4 Optimization search to covarian
Page 57: 3.4 Optimization Hence for the case
Page 61 and 62: 3.4 Optimization tained without app
Page 63 and 64: = π R 2 0 dt ǫ + R2 = π log , ǫ
Page 65 and 66: 3.4 Optimization where the bound is
Page 67 and 68: 3.4 Optimization wheren is the matr
Page 69 and 70: 3.4 Optimization Lemma 3.10: The ou
Page 71 and 72: 3.5 Optical implementation The wei
Page 73 and 74: 3.6 Teleportation criteria can be t
Page 75 and 76: 3.6 Teleportation criteria carry th
Page 77: Quantum Cellular Automata
Page 80 and 81: 4 Gaussian quantum cellular automat
Page 108 and 109:
4 Gaussian quantum cellular automat
Page 111 and 112:
5 Gaussian private quantum channels
Page 113 and 114:
p Figure 5.1: Illustrating the encr
Page 115 and 116:
characteristic function χrand(ξ)
Page 117 and 118:
= − 1 2 2Nf i,j=1 where M ′ =
Page 119 and 120:
p δ ξk ξ x 5.2 Security estimati
Page 121 and 122:
5.2 Security estimation where in th
Page 123 and 124:
5.3 Result and outlook 5.3 Result a
Page 125:
Bibliography
Page 128 and 129:
Bibliography [7] M. Reed and B. Sim
Page 130 and 131:
Bibliography [37] R. F. Werner,Opti
Page 132 and 133:
Bibliography [69] N. Takei, H. Yone
Page 134 and 135:
Bibliography 124
show all

Quantum Information Theory with Gaussian Systems

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?