Download - NASA
Download - NASA
Download - NASA
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
Rotor 97<br />
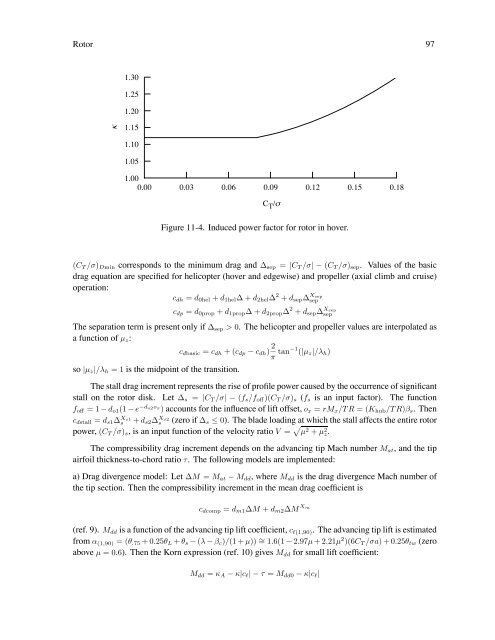
κ<br />
1.30<br />
1.25<br />
1.20<br />
1.15<br />
1.10<br />
1.05<br />
1.00<br />
0.00 0.03 0.06 0.09 0.12 0.15 0.18<br />
C T /σ<br />
Figure 11-4. Induced power factor for rotor in hover.<br />
(CT /σ)Dmin corresponds to the minimum drag and Δsep = |CT /σ| −(CT /σ)sep. Values of the basic<br />
drag equation are specified for helicopter (hover and edgewise) and propeller (axial climb and cruise)<br />
operation:<br />
cdh = d0hel + d1helΔ+d2helΔ 2 + dsepΔ Xsep<br />
sep<br />
cdp = d0prop + d1propΔ+d2propΔ 2 + dsepΔ Xsep<br />
sep<br />
The separation term is present only if Δsep > 0. The helicopter and propeller values are interpolated as<br />
a function of μz:<br />
cdbasic = cdh +(cdp − cdh) 2<br />
π tan−1 (|μz|/λh)<br />
so |μz|/λh =1is the midpoint of the transition.<br />
The stall drag increment represents the rise of profile power caused by the occurrence of significant<br />
stall on the rotor disk. Let Δs = |CT /σ| −(fs/foff)(CT /σ)s (fs is an input factor). The function<br />
foff =1− do1(1 − e −do2ox ) accounts for the influence of lift offset, ox = rMx/T R =(Khub/T R)βs. Then<br />
cdstall = ds1Δ Xs1<br />
s<br />
+ ds2Δ Xs2<br />
s<br />
(zero if Δs ≤ 0). The blade loading at which the stall affects the entire rotor<br />
power, (CT /σ)s, is an input function of the velocity ratio V = μ 2 + μ 2 z.<br />
The compressibility drag increment depends on the advancing tip Mach number Mat, and the tip<br />
airfoil thickness-to-chord ratio τ. The following models are implemented:<br />
a) Drag divergence model: Let ΔM = Mat − Mdd, where Mdd is the drag divergence Mach number of<br />
the tip section. Then the compressibility increment in the mean drag coefficient is<br />
cdcomp = dm1ΔM + dm2ΔM Xm<br />
(ref. 9). Mdd is a function of the advancing tip lift coefficient, c ℓ(1,90). The advancing tip lift is estimated<br />
from α (1,90) =(θ.75 +0.25θL + θs − (λ − βc)/(1 + μ)) ∼ = 1.6(1 − 2.97μ +2.21μ 2 )(6CT /σa)+0.25θtw (zero<br />
above μ =0.6). Then the Korn expression (ref. 10) gives Mdd for small lift coefficient:<br />
Mdd = κA − κ|cℓ|−τ = Mdd0 − κ|cℓ|