A review of the dense Z-pinch

Plasma Phys. Control. Fusion 53 (2011) 093001
Topical Review
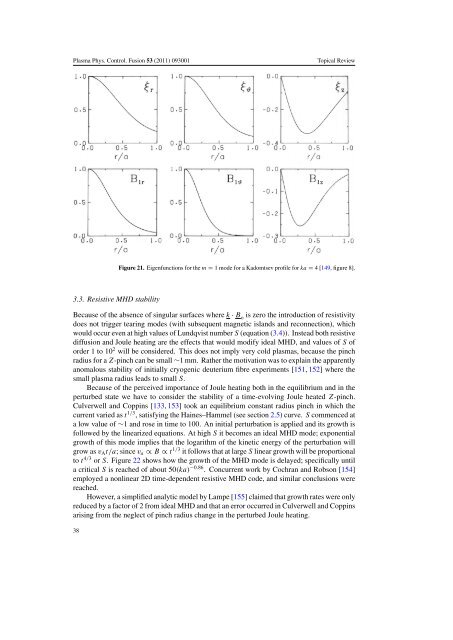
Figure 21. Eigenfunctions for the m = 1 mode for a Kadomtsev profile for ka = 4[149, figure 8].
3.3. Resistive MHD stability
Because of the absence of singular surfaces where k · B o is zero the introduction of resistivity
does not trigger tearing modes (with subsequent magnetic islands and reconnection), which
would occur even at high values of Lundqvist number S (equation (3.4)). Instead both resistive
diffusion and Joule heating are the effects that would modify ideal MHD, and values of S of
order 1 to 10 2 will be considered. This does not imply very cold plasmas, because the pinch
radius for a Z-pinch can be small ∼1 mm. Rather the motivation was to explain the apparently
anomalous stability of initially cryogenic deuterium fibre experiments [151, 152] where the
small plasma radius leads to small S.
Because of the perceived importance of Joule heating both in the equilibrium and in the
perturbed state we have to consider the stability of a time-evolving Joule heated Z-pinch.
Culverwell and Coppins [133, 153] took an equilibrium constant radius pinch in which the
current varied as t 1/3 , satisfying the Haines–Hammel (see section 2.5) curve. S commenced at
a low value of ∼1 and rose in time to 100. An initial perturbation is applied and its growth is
followed by the linearized equations. At high S it becomes an ideal MHD mode; exponential
growth of this mode implies that the logarithm of the kinetic energy of the perturbation will
grow as v A t/a; since v a ∝ B ∝ t 1/3 it follows that at large S linear growth will be proportional
to t 4/3 or S. Figure 22 shows how the growth of the MHD mode is delayed; specifically until
a critical S is reached of about 50(ka) −0.86 . Concurrent work by Cochran and Robson [154]
employed a nonlinear 2D time-dependent resistive MHD code, and similar conclusions were
reached.
However, a simplified analytic model by Lampe [155] claimed that growth rates were only
reduced by a factor of 2 from ideal MHD and that an error occurred in Culverwell and Coppins
arising from the neglect of pinch radius change in the perturbed Joule heating.
38