A review of the dense Z-pinch

More documents

Recommendations

Info

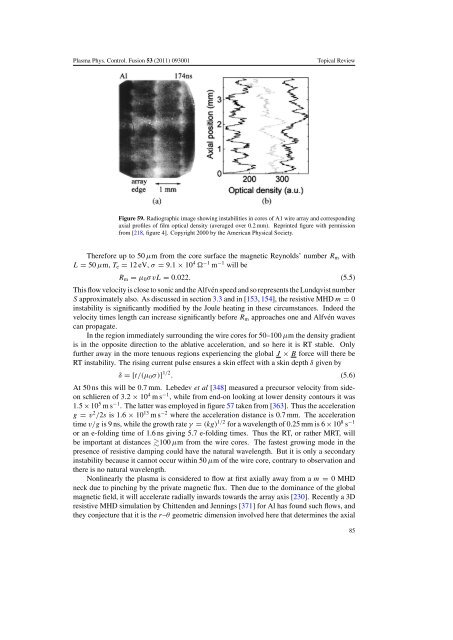
Plasma Phys. Control. Fusion 53 (2011) 093001 Topical Review Figure 59. Radiographic image showing instabilities in cores of A1 wire array and corresponding axial profiles of film optical density (averaged over 0.2 mm). Reprinted figure with permission from [218, figure 4]. Copyright 2000 by the American Physical Society. Therefore up to 50 µm from the core surface the magnetic Reynolds’ number R m with L = 50 µm, T e = 12 eV, σ = 9.1 × 10 4 −1 m −1 will be R m = µ 0 σvL = 0.022. (5.5) This flow velocity is close to sonic and the Alfvén speed and so represents the Lundqvist number S approximately also. As discussed in section 3.3 and in [153, 154], the resistive MHD m = 0 instability is significantly modified by the Joule heating in these circumstances. Indeed the velocity times length can increase significantly before R m approaches one and Alfvén waves can propagate. In the region immediately surrounding the wire cores for 50–100 µm the density gradient is in the opposite direction to the ablative acceleration, and so here it is RT stable. Only further away in the more tenuous regions experiencing the global J × B force will there be RT instability. The rising current pulse ensures a skin effect with a skin depth δ given by δ = [t/(µ 0 σ)] 1/2 . (5.6) At 50 ns this will be 0.7 mm. Lebedev et al [348] measured a precursor velocity from sideon schlieren of 3.2 × 10 4 ms −1 , while from end-on looking at lower density contours it was 1.5 × 10 5 ms −1 . The latter was employed in figure 57 taken from [363]. Thus the acceleration g = v 2 /2s is 1.6 × 10 13 ms −2 where the acceleration distance is 0.7 mm. The acceleration time v/g is 9 ns, while the growth rate γ = (kg) 1/2 for a wavelength of 0.25 mm is 6 × 10 8 s −1 or an e-folding time of 1.6 ns giving 5.7 e-folding times. Thus the RT, or rather MRT, will be important at distances 100 µm from the wire cores. The fastest growing mode in the presence of resistive damping could have the natural wavelength. But it is only a secondary instability because it cannot occur within 50 µm of the wire core, contrary to observation and there is no natural wavelength. Nonlinearly the plasma is considered to flow at first axially away from a m = 0 MHD neck due to pinching by the private magnetic flux. Then due to the dominance of the global magnetic field, it will accelerate radially inwards towards the array axis [230]. Recently a 3D resistive MHD simulation by Chittenden and Jennings [371] for Al has found such flows, and they conjecture that it is the r–θ geometric dimension involved here that determines the axial 85
Plasma Phys. Control. Fusion 53 (2011) 093001 Topical Review wavelength. Initial fine-scale random perturbations of temperature in the core were introduced in order to seed the instability. Earlier 2D and 3D simulations by Frese et al [372] as well as Garasi et al [360] also contributed usefully to understanding the physics. The emphasis here was to question the notion that merger of plasmas from separate wires occurs and leads to the formation of a shell, rather than to the inward flow of separate plasma jets. Axial wave numbers would be characteristic of a thermal instability in a conductor in which the resistivity η increases with temperature T and the current is in the axial direction. The instability arises because in a region of increased temperature but current density continuous, the heating rate ηJ 2 will be increased, so increase the temperature further. However dη/dT is > 0 for W at solid density only below 1 eV and as the density is dropped the point where dη/dT = 0 moves to lower temperature. For Al, dη/dT is >0 at solid density below 6 eV and is less pronounced as the density drops. Short wavelengths would be damped by thermal conduction, but there does not appear to be a mechanism to give a natural wavelength, and certainly for W, the dη/dT > 0 effect disappears in typical corona close to the wire core. Further discussion on this can be found in [738] including the composition with MHD modes. The fourth candidate is the heat-flow driven electrothermal instability, proposed for conditions of nonlinear heat flow such as near the ablation surface of an ICF capsule [214], where the heat flow is 3% of the free-streaming limit. It is discussed in detail in section 3.12. A second necessary condition is given by equations (3.50) and (3.51). Taking equation (3.52) and inserting for W with Z = 6 and T e = 12 eV and a wavelength λ of 0.25 mm this instability will occur at an electron density of n e of 6.8×10 25 m −3 or a density of 3.5 kg m −3 . Referring to figure 46, it can be seen that this is the density at 50–100 µm from the wire core. Further in, at high density this and shorter wavelengths will be locally unstable, but the shorter wavelengths will be damped by thermal conduction as the plasma ablates and the density drops. Perhaps this occurs in the experiment of Jones et al [219]. The condition (3.51) is well satisfied. The growth rate (equation (3.53)) is 6.3×10 8 s −1 or an e-folding time of 1.6 ns compared with the ablation transit time of 13 ns. For Al with Z = 2; T e = 12 eV and a wavelength of 0.5 mm, this will be the fastest growing mode at a density of 0.43 kg m −3 . Shorter wavelengths will occur at higher density or lower temperatures. In this theoretical model there is no radiation transport, but very close to the high density wire cores the thermal conduction is more important. Furthermore the process of ablation of ions requires, in this range of density, the frictional drag by the cold return current associated with the nonlinear heat flow [215]. The perturbations in return current flow will lead to perturbations in the mass ablation rate, leading eventually to gaps. It can also be argued that radiation transport also leads to a thermoelectric field due to photon momentum deposition, and hence a return cold current which can be thermally unstable. To summarize, the electrothermal heat-flow instability will occur close to the wire cores and a natural wavelength emerges as the fastest growing mode where the plasma exits the core interaction region. Unfortunately, it cannot be modelled by present fluid simulations, and requires at least a hybrid code. Probing the wires with MeV protons [217] should resolve the issue as the electrothermal instability occurs at high density and low temperature, i.e. close to the cores. In a recent experiment using the Cornell Beam Research Accelerator (COBRA) by Knap et al [373] the axial wavelength and amplitude of the instability together with the core radius were measured as a function of time using laser shadowgraphy. It was found that both grew from ∼0.1 mm to ∼0.5 mm over 30 ns from breakdown. At this time there is saturation, and the wavelength is essentially the fundamental wavelength that had been measured in earlier experiments. The saturation is believed to be associated with the inward flow of precursor plasma and change in magnetic topology, similar to MHD simulations [371]. B-dot probes show the reduction in the initial private magnetic flux around each wire and the dominance of the global field (see figure 50(b)) by this time. 86
Page 1 and 2:
Home Search Collections Journals Ab
Page 3 and 4:
Plasma Phys. Control. Fusion 53 (20
Page 5 and 6:
Page 7 and 8:
Page 9 and 10:
Page 11 and 12:
Page 13 and 14:
Page 15 and 16:
Page 17 and 18:
Page 19 and 20:
Page 21 and 22:
Page 23 and 24:
Page 25 and 26:
Page 27 and 28:
Page 29 and 30:
Page 31 and 32:
Page 33 and 34:
Page 35 and 36: Plasma Phys. Control. Fusion 53 (20
Page 85: Plasma Phys. Control. Fusion 53 (20
Page 137 and 138:
Page 139 and 140:
Page 141 and 142:
Page 143 and 144:
Page 145 and 146:
Page 147 and 148:
Page 149 and 150:
Page 151 and 152:
Page 153 and 154:
Page 155 and 156:
Page 157 and 158:
Page 159 and 160:
Page 161 and 162:
Page 163 and 164:
Page 165 and 166:
Page 167 and 168:
Page 169:
show all

A review of the dense Z-pinch

Create successful ePaper yourself

Delete template?

Save as template?