BABSc, B.Com & BCA Questions _III - Nalanda Open University
BABSc, B.Com & BCA Questions _III - Nalanda Open University
BABSc, B.Com & BCA Questions _III - Nalanda Open University
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
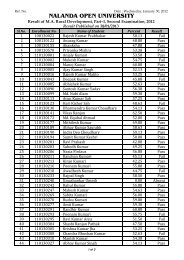
<strong>Nalanda</strong> <strong>Open</strong> <strong>University</strong><br />
Annual Exam-2010,<br />
Bachelor of Science (Mathematics) Hons, Part-<strong>III</strong><br />
Paper-VI<br />
Time: 3Hrs Full Marks: 75<br />
Answer Six questions, selecting at least one question from each group.<br />
Group-A<br />
1. (a) Define centre of a group. Show that the centre of a group G is a normal subgroup of G.<br />
(b) Let f be a function on the group G defined by f(x) = x -1 for each x in G. Show that f is an<br />
automorphism if and only if G is abelian.<br />
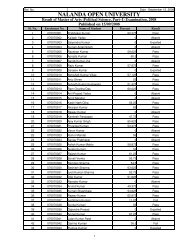
2. (a) Let f R T be an isomorphism of the ring R onto the ring T. If O and O ' are the<br />
zero elements of R and T respectively, show that f(O) = O' and f(-a) = -f(a) for all<br />
a in R.<br />
(b) Show by an example that if I and J are ideals in R, then I U J is not an ideal in R.<br />
3. Let R be a commutative ring with unity 1. Let M be an ideal in R. Then prove that<br />
R / M is a field if and only if M is a maximal ideal in R.<br />
4. Show that any ring can be embedded in a ring with unity.<br />
Group-B<br />
5. For any cardinals α, β, γ show that<br />
β γ β + γ<br />
(i) α . α = α (ii) αβ<br />
γ α γ β γ<br />
b g =<br />
6. (a) If E is any set then show that Card P(E) = 2 CardE<br />
where P(E) denotes the power set of E.<br />
(b) If α and β are cardinal numbers such that α β β α . Prove that α β .<br />
7. (a) Prove that the order type of the set of all real numbers in the open interval (a, b)<br />
with usual order is λ .<br />
(b) State and prove Zorn's lemma.<br />
Group-C<br />
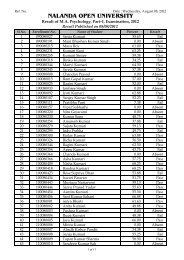
8. (a) Find the mean and variance of a Binomial distribution.<br />
(b) 6 die are thrown 729 times. How many times you expect at least 3 dice to show a<br />
five or six.<br />
9. (a) Find an explicit formula for the Fibonacci numbers.<br />
(b) Illustrate how generating function can be used to get the number of r-<br />
combinations from a set with n elements when repition of elements is allowed.<br />
Group-D<br />
10. (a) Show that the function<br />
f ( z) = xy<br />
is not analytic at the origin although the<br />
Cauchy - Riemann equations are satisfied at the point.<br />
(b) Construct the analytic function f(z) = u + iv where<br />
u = x 3 - 3xy 2 + 3x+1<br />
11. State and prove Laurent's theorem.<br />
12. (a) Explain different types of singularities with examples.<br />
CotπZ<br />
2<br />
(b) Find kind of singularities of ( z − a)<br />
at Z=a and Z = ∞ .<br />
****