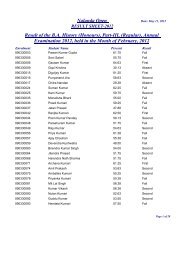
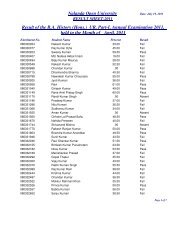
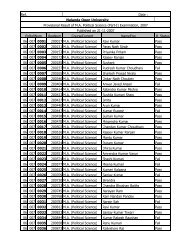
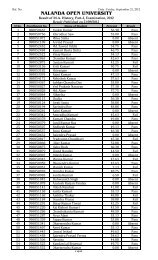
BABSc, B.Com & BCA Questions _III - Nalanda Open University

Nalanda Open University
Annual Exam-2010,
Bachelor in Computer Application, Part-III
Paper-XVII (CS-71)
Time: 3Hrs Full Marks: 75
Answer any five questions. All questions are of equal marks. Calculators are
allowed.
1. Solve the system of equations by Gauss Seidel iteration method
10x 1 - 2x 2 - x 3 - x 4 = 3
-2x 1 + 10x 2 - x 3 - x 4 = 15
-x 1 - x 2 + 10x 3 - 2x 4 = 27
-x 1 - x 2 - 2x 3 + 10x 4 = - 9
2. Using the Newton-Raphson method find the square root of 10 with initial
approximation x 0 = 3.
3. Using modified Euler's method find the value of y at x = 0.2 with h=0.1 where
dy
= 1− y with y( 0)
= 0
dx
4. Using the following table find f 1 (5)
x 0 2 3 4 7 9
y=f(x) 4 26 58 112 466 922
5. Using the fourth order Taylor's series method find the solution of the differential
equations.
y 1 = x - y 2 , y(0) = 1
Find y(0.1) taking h = 0.1.
6. Use Runge-Kutta method of fourth order to estimate y(0.2) of the equation
dy y = 3 x + , y ( 0)
= 1
dx 2
by taking h = 0.2
z
5.
2
loge x dx
7. Evaluate 4 taking 6 equal parts by applying Simpson's
dy
8. Find dx and d 2
y
2
dx at x = 1 and r = 0 from the following data
x 0 2 4 6 8
y 7 13 43 145 367
9. Estimate the value of f(1.45) from the following data given below
x 1.1 1.2 1.3 1.4 1.5
f(x) 1.3357 1.5095 1.6984 1.9043 2.1293
10. State and Prove Bisection method.
********
3
8 th Rule.