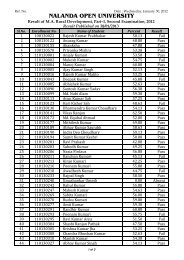
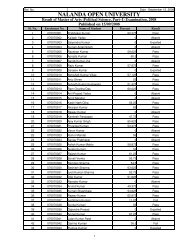
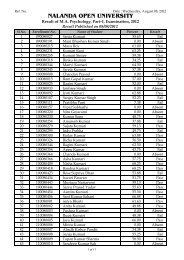
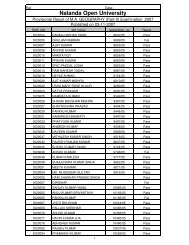
BABSc, B.Com & BCA Questions _III - Nalanda Open University
BABSc, B.Com & BCA Questions _III - Nalanda Open University
BABSc, B.Com & BCA Questions _III - Nalanda Open University
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
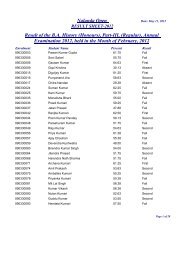
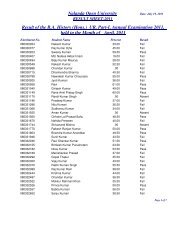
<strong>Nalanda</strong> <strong>Open</strong> <strong>University</strong><br />
Annual Exam-2010,<br />
Bachelor of Science (Mathematics) Hons, Part-<strong>III</strong><br />
Paper-VII<br />
Time: 3Hrs Full Marks: 75<br />
Answer Six questions, selecting at least one question from each group.<br />
Group-A<br />
1. (a) Prove that the set of all convex combinations of a finite number of linearly independent<br />
vectors V 1 , V 2 , V 3 , ....., V m is a convex set.<br />
(b) Solve the following L.P. problem graphically.<br />
Max Z = 5x+7y<br />
subject to the following constraints<br />
x + y ≤ 4<br />
2. Use the simplex method to solve<br />
Max Z = 3x 1 +9x 2<br />
subject to<br />
x + 4x<br />
≤ 8<br />
x<br />
1 2<br />
+ 2x<br />
≤ 4<br />
1 2<br />
3x<br />
+ 8y<br />
≤ 24<br />
10x<br />
+ 7y<br />
≤ 35<br />
x,<br />
y ≥ 0<br />
x1,<br />
x2<br />
≥ 0<br />
3. Obtain an initial basic feasible solution to the following transportation problem<br />
using the north-west corner method<br />
D E F G Available<br />
A 11 13 17 14 250<br />
B 16 18 14 10 300<br />
C 21 24 13 10 400<br />
Requirement 200 225 275 250<br />
Group-B<br />
4. (a) Solve (y 2 +yz+z 2 )dx+(z 2 +zx+x 2 )dy+(x 2 +xy+y 2 )dz=0<br />
(b) Solve<br />
dx dy dz<br />
= =<br />
2 2 2<br />
x − yz y − zx z − xy<br />
5. (a) Apply Charpit's method to find complete integral p 2 +q 2 -2px-2qy+1=0.<br />
(b) Solve the following Lagrange's equation (y 3 x-2x 4 )p+(2y 4 -x 3 y)q=9z(x 3 -y 3 ).<br />
6. (a) Solve r = b 2 t.<br />
(b) Find the solution of Lagrange's differential equation pq+Qq=R.<br />
7. (a) Find the orthogonal projection on the xz-plane of the curves which lie on the<br />
paraboloid 3z=x 2 +y 2 and satisfy the equation 2dz = (x+z) dx+ydy.<br />
dx<br />
x y t dy<br />
2<br />
+ 2 − 3 = , − 3x + 2y = e t<br />
(b) Solve the simiultaneous equations dt<br />
dt<br />
.<br />
Group-C<br />
8. (a) Find the attraction of a thin uniform spherical shell at an internal point.<br />
(b) A uniform solid sphere of mass M is cut in 2 parts by a diametral plane. Prove<br />
2<br />
3<br />
γ M 2<br />
that the resultant attraction between the halves is 16 a , where a is the radius<br />
of the sphere and γ the constant of gravitation.