BABSc, B.Com & BCA Questions _III - Nalanda Open University
BABSc, B.Com & BCA Questions _III - Nalanda Open University
BABSc, B.Com & BCA Questions _III - Nalanda Open University
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
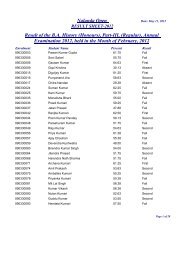
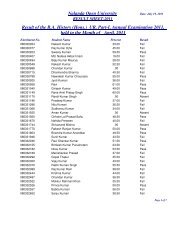
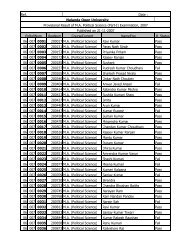
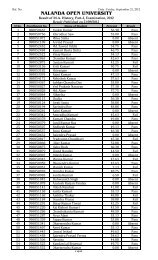
<strong>Nalanda</strong> <strong>Open</strong> <strong>University</strong><br />
Annual Exam-2010,<br />
Bachelor of Science (Physics) Hons, Part-<strong>III</strong><br />
(Quantum Mechanics & Statistical Mechanics)<br />
Paper-VI<br />
Time: 3 Hrs Full Marks: 75<br />
Answer any FIVE questions. All questions are of equal marks.<br />
1. (a) Show that two eigen functions of Hermitian operators, belonging to different<br />
eigenvalues are orthogonal.<br />
(b) A ball of mass 10 gm. has velocity 100 cm/sec. Calculate the wavelength<br />
associated with it. Why does not this wave nature show up in our daily<br />
observations?<br />
(Given h= 6.62 × 10 -34 Joule.Sec)<br />
2. Derive time dependent SchrÖdinger equation for the motion of a non-relativistic<br />
material particle.<br />
3. A particle of mass m and total energy E moves from a region of zero potential ( v<br />
(x) = 0 When x < 0 ) to a region of constant potential<br />
( v<br />
(x) = V 0 When x > 0 ). Derive expressions for the reflection and transmission<br />
coefficients.<br />
4. A particle of mass m moving freely along the x-axis between two rigid walls<br />
situated at x = 0 and x = L. Determine the allowed values of energy and the<br />
corresponding normalised wave functions.<br />
5. Define angular momentum. Show that the components of angular momentum do<br />
not commute.<br />
6. Write the possible states of the He- atom and write down its Hamiltonian. Hence<br />
find the ground state of He- atom and its energy.<br />
7. State and prove Liouville's theorem.<br />
8. Apply grand canonical ensemble theory to obtain free energy and internal energy of<br />
a perfect gas.<br />
9. Find the relation between pressure and temperature of vapour treated as a gas<br />
during liquid-vapour transition.<br />
10. Establish the Fermi-Dirac distribution formula and hence obtain an expression for<br />
Fermi energy.<br />
κ κ κ