BABSc, B.Com & BCA Questions _III - Nalanda Open University
BABSc, B.Com & BCA Questions _III - Nalanda Open University
BABSc, B.Com & BCA Questions _III - Nalanda Open University
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
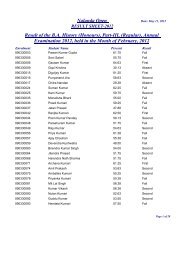
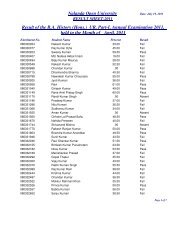
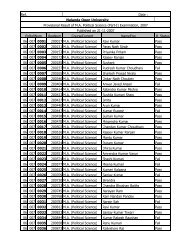
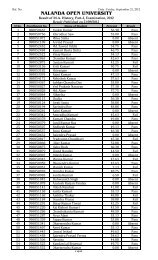
<strong>Nalanda</strong> <strong>Open</strong> <strong>University</strong><br />
Annual Exam-2010,<br />
Bachelor of Science (Mathematics) Hons, Part-<strong>III</strong><br />
Paper-V<strong>III</strong><br />
Time: 3Hrs Full Marks: 75<br />
Answer any Five questions. All questions carry equal marks.<br />
Calculator are Allowed.<br />
1. (a) Evaluate<br />
2 2<br />
∆<br />
∆<br />
E Sin x h Sin( x + h)<br />
( + ) +<br />
ESin( x + h)<br />
h being the differencing interval.<br />
(b) Given that log 10 654 = 2.8156, log 10 658 = 2.8182, log 10 659 = 2.8189, log 10 661 =<br />
2.8202 find the value of log 10 656 by Lagrange's Interpolation formula.<br />
2. (a) Establish Gauss Forward Interpolation formula for equal Interval.<br />
(b) Find the missing term in the following table<br />
x: 16 18 20 22 24 26<br />
y: 39 85 - 151 264 388<br />
3. (a) Find the first and 2nd derevatives of the function y = f(x) tabulated below at the<br />
point x = 1.1<br />
x 1 1.2 1.4 1.6 1.8 2.00<br />
f(x) 0.00 0.1280 0.5440 1.2960 2.4320 4.00<br />
(b) Prove that the nth divided differences of a polynomial of the nth degree are<br />
constant.<br />
4. (a) Derive trapezoidal Rule for numerical evaluation of integrals.<br />
z5.<br />
2<br />
lo g x d x<br />
4<br />
(b) Find by Weddle's rule the value of<br />
e .<br />
5. (a) Solve 2U x+2 - 5U x+1 +2U x =0 find the Particular solution when U o =1, U 1 = 1.<br />
dy y x<br />
(b) Given dx<br />
y x Euler's method.<br />
6. (a) Explain Picard's method of successive Approximation.<br />
dy 1<br />
= x + y<br />
(b) Find y(2) if y(x) is the solution of dx 2 ( ) assuming y(0) = 2, y(0.5) =<br />
2.636,<br />
y(1) = 3.595, y(1.5)=4.968 by Milne's Method.<br />
7. (a) Explain Gauss elimination method.<br />
(b) Solve the system of Equations by Gauss - Seidal Iteration method<br />
27x+6y-z=85<br />
6x+15y+2z=72<br />
x+y+54z=110<br />
8. (a) Explain method of finding the roots and equation by Bisection Method.<br />
(b) Find the real roots of the Equation with the help of Reguli falsi method xlog 10 x -<br />
1.2 = 0.<br />
9. Explain Newton-Raphson's method and find the root of x 4 - x - 10 nearer to x = 2<br />
correct to three decimal places with the help of Newton Raphson's method.<br />
10. Use Greaff's method to solve the Equation x 3 - 5x 2 - 17x + 20 = 0.<br />
******<br />
vko';d lwpuk