To the Graduate Council: I am submitting herewith a thesis written by ...

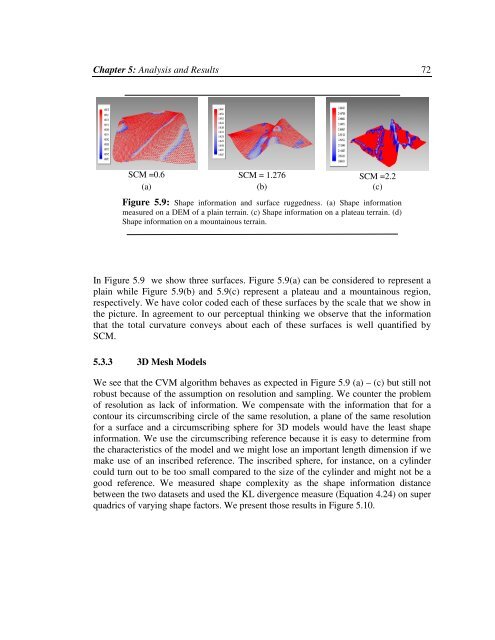
Chapter 5: Analysis and Results 72SCM =0.6 SCM = 1.276 SCM =2.2(a) (b) (c)Figure 5.9: Shape information and surface ruggedness. (a) Shape informationmeasured on a DEM of a plain terrain. (c) Shape information on a plateau terrain. (d)Shape information on a mountainous terrain.In Figure 5.9 we show three surfaces. Figure 5.9(a) can be considered to represent aplain while Figure 5.9(b) and 5.9(c) represent a plateau and a mountainous region,respectively. We have color coded each of these surfaces by the scale that we show inthe picture. In agreement to our perceptual thinking we observe that the informationthat the total curvature conveys about each of these surfaces is well quantified bySCM.5.3.3 3D Mesh ModelsWe see that the CVM algorithm behaves as expected in Figure 5.9 (a) – (c) but still notrobust because of the assumption on resolution and sampling. We counter the problemof resolution as lack of information. We compensate with the information that for acontour its circumscribing circle of the same resolution, a plane of the same resolutionfor a surface and a circumscribing sphere for 3D models would have the least shapeinformation. We use the circumscribing reference because it is easy to determine fromthe characteristics of the model and we might lose an important length dimension if wemake use of an inscribed reference. The inscribed sphere, for instance, on a cylindercould turn out to be too small compared to the size of the cylinder and might not be agood reference. We measured shape complexity as the shape information distancebetween the two datasets and used the KL divergence measure (Equation 4.24) on superquadrics of varying shape factors. We present those results in Figure 5.10.