Equilibrium Growth, Inflation, and Bond Yields - Duke University's ...

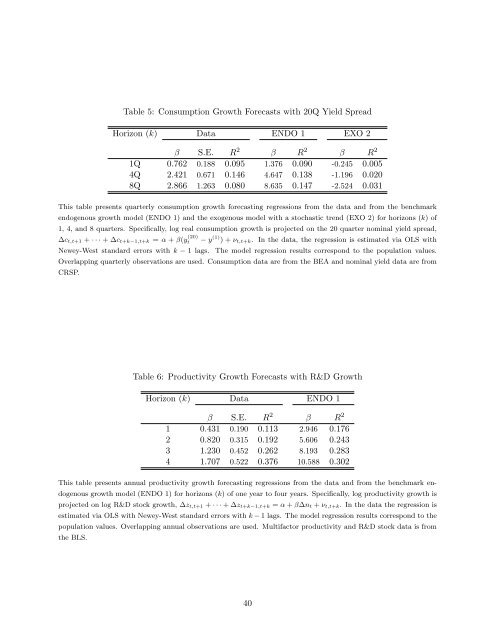
Table 5: Consumption Growth Forecasts with 20Q Yield Spread
Horizon (k) Data ENDO 1 EXO 2
β S.E. R 2 β R 2 β R 2
1Q 0.762 0.188 0.095 1.376 0.090 -0.245 0.005
4Q 2.421 0.671 0.146 4.647 0.138 -1.196 0.020
8Q 2.866 1.263 0.080 8.635 0.147 -2.524 0.031
This table presents quarterly consumption growth forecasting regressions from the data and from the benchmark
endogenous growth model (ENDO 1) and the exogenous model with a stochastic trend (EXO 2) for horizons (k) of
1, 4, and 8 quarters. Specifically, log real consumption growth is projected on the 20 quarter nominal yield spread,
∆ct,t+1 + · · · + ∆ct+k−1,t+k = α + β(y (20)
t − y (1) ) + νt,t+k. In the data, the regression is estimated via OLS with
Newey-West standard errors with k − 1 lags. The model regression results correspond to the population values.
Overlapping quarterly observations are used. Consumption data are from the BEA and nominal yield data are from
CRSP.
Table 6: Productivity Growth Forecasts with R&D Growth
Horizon (k) Data ENDO 1
β S.E. R 2 β R 2
1 0.431 0.190 0.113 2.946 0.176
2 0.820 0.315 0.192 5.606 0.243
3 1.230 0.452 0.262 8.193 0.283
4 1.707 0.522 0.376 10.588 0.302
This table presents annual productivity growth forecasting regressions from the data and from the benchmark en-
dogenous growth model (ENDO 1) for horizons (k) of one year to four years. Specifically, log productivity growth is
projected on log R&D stock growth, ∆zt,t+1 + · · · + ∆zt+k−1,t+k = α + β∆nt + νt,t+k. In the data the regression is
estimated via OLS with Newey-West standard errors with k − 1 lags. The model regression results correspond to the
population values. Overlapping annual observations are used. Multifactor productivity and R&D stock data is from
the BLS.
40