Termofysiikan perusteet, Ismo Napari ja Hanna Vehkamäki, 2013.

TermofysiikanperusteetIsmo Napari ja Hanna VehkamäkiT 2∆Q 2C∆W∆Q 1T 1 (< T 2 )Helsingin yliopisto, 2013(Päivitetty 18. joulukuuta 2013)

Sisältö1 Johdanto 11.1 Termofysiikan osa-alueet . . . . . . . . . . . . . . . . . . . . . . . 11.2 Termodynamiikan käsitteistöä (1.3) . . . . . . . . . . . . . . . . . 21.3 Ideaalikaasun tilanyhtälö (1.2, 1.4) . . . . . . . . . . . . . . . . . 31.4 Esimerkkejä tilanyhtälöistä (1.5, 7.2) . . . . . . . . . . . . . . . . 61.4.1 Reaalikaasun viriaalikehitelmä . . . . . . . . . . . . . . . 61.4.2 Van der Waalsin tilanyhtälö . . . . . . . . . . . . . . . . . 61.4.3 Curien laki . . . . . . . . . . . . . . . . . . . . . . . . . . . 72 Termodynamiikan nollas pääsääntö 82.1 Termodynaaminen tasapaino (1.3) . . . . . . . . . . . . . . . . . 82.2 Lämpömittarit ja lämpötila-asteikot (1.2) . . . . . . . . . . . . . . 93 Termodynamiikan ensimmäinen pääsääntö 123.1 Työ (2.2, 2.7) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123.2 Eksaktit ja epäeksaktit differentiaalit (3.1) . . . . . . . . . . . . . 153.3 Termodynamiikan ensimmäinen pääsääntö (2.3, 2.1) . . . . . . . 183.3.1 Mitä lämpö on? . . . . . . . . . . . . . . . . . . . . . . . . 183.3.2 Energia säilyy . . . . . . . . . . . . . . . . . . . . . . . . . 193.4 Lämpökapasiteetit (2.5) . . . . . . . . . . . . . . . . . . . . . . . . 213.5 Kvasistaattisia ideaalikaasuprosesseja (˜2.1, 2.11) . . . . . . . . . 233.5.1 Isoterminen prosessi . . . . . . . . . . . . . . . . . . . . . 233.5.2 Isobaarinen prosessi . . . . . . . . . . . . . . . . . . . . . 243.5.3 Isokoorinen prosessi . . . . . . . . . . . . . . . . . . . . . 253.5.4 Adiabaattinen prosessi . . . . . . . . . . . . . . . . . . . . 254 Termodynamiikan toinen pääsääntö 294.1 Toinen pääsääntö ja Carnot’n kone (5.2) . . . . . . . . . . . . . . 294.2 Absoluuttinen lämpötila (5.14) . . . . . . . . . . . . . . . . . . . 344.3 Carnot’n jääkaappi ja lämpöpumppu (5.11) . . . . . . . . . . . . 354.4 Ideaalikaasukoneita (5.2) . . . . . . . . . . . . . . . . . . . . . . . 374.4.1 Carnot’n kone . . . . . . . . . . . . . . . . . . . . . . . . . 374.4.2 Otto-kiertoprosessi . . . . . . . . . . . . . . . . . . . . . . 394.5 Clausiuksen epäyhtälö (5.6) . . . . . . . . . . . . . . . . . . . . . 41

SISÄLTÖiii4.6 Entropia (5.3) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 434.6.1 Entropia ja ensimmäinen pääsääntö . . . . . . . . . . . . 454.6.2 Mitä entropia oikein kuvaa? . . . . . . . . . . . . . . . . . 464.7 Sisäinen energia ja Maxwellin relaatiot (6.2) . . . . . . . . . . . . 474.7.1 Fundamentaalinen yhtälö (˜6.4) . . . . . . . . . . . . . . . 484.7.2 Gibbsin ja Duhemin yhtälö . . . . . . . . . . . . . . . . . 494.7.3 Mikä on kemiallinen potentiaali ja miksi se riippuu paineestaja lämpötilasta? . . . . . . . . . . . . . . . . . . . . 504.8 Esimerkkejä entropian muutoksen laskemisesta (5.4) . . . . . . . 504.8.1 Ideaalikaasun isoterminen reversiibeli laajeneminen . . . 504.8.2 Ideaalikaasun irreversiibeli ja adiabaattinen vapaa laajeneminen. . . . . . . . . . . . . . . . . . . . . . . . . . . . 514.8.3 Kappaleen lämmitys isokoorisesti tai isobaarisesti . . . . 514.8.4 Sekoitusentropia . . . . . . . . . . . . . . . . . . . . . . . 524.9 Entropian differentiaali ja eräitä sovelluksia (5.12, 3.1, 3.5) . . . . 544.9.1 Helmholtzin yhtälö . . . . . . . . . . . . . . . . . . . . . . 544.9.2 Ideaalikaasun entropia . . . . . . . . . . . . . . . . . . . . 554.9.3 Lämpökapasiteettiyhtälöt . . . . . . . . . . . . . . . . . . 554.10 Termodynamiikan kolmas pääsääntö (5.8) . . . . . . . . . . . . . 584.11 Termodynamiikan pääsäännöt: suppea kooste . . . . . . . . . . 594.12 Pisaran tarina, osa 1: taustaa ja tasapainoehdot termodynamiikantoisen pääsäännön avulla (˜8.8) . . . . . . . . . . . . . . . . . 594.12.1 Pisaranmuodostus ja ilmakehä . . . . . . . . . . . . . . . 594.12.2 Tasopinnan faasitasapaino . . . . . . . . . . . . . . . . . . 614.12.3 Pisaran faasitasapaino . . . . . . . . . . . . . . . . . . . . 645 Termodynaamiset potentiaalit eli vapaat energiat 665.1 Systeemin sisäistä tilaa kuvaavat muuttujat . . . . . . . . . . . . 665.2 Ympäristön kanssa vuorovaikuttavat systeemit (5.7, 6.1) . . . . 675.3 Vapaat energiat ja niiden tasapainoarvojen derivaatat (2.9, 2.10,6.2) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 725.3.1 Helmholtzin vapaa energia . . . . . . . . . . . . . . . . . 725.3.2 Gibbsin vapaa energia . . . . . . . . . . . . . . . . . . . . 745.3.3 Entalpia . . . . . . . . . . . . . . . . . . . . . . . . . . . . 755.3.4 Suuri potentiaali . . . . . . . . . . . . . . . . . . . . . . . 765.4 Miksi termodynaamisia potentiaaleja kutsutaan myös vapaiksienergioiksi? (6.1) . . . . . . . . . . . . . . . . . . . . . . . . . . . 775.4.1 Joulen ja Thomsonin ilmiö (3.7) . . . . . . . . . . . . . . 805.5 Pisaran tarina, osa 2: vapaan energian muutos pisaran muodostumisessa. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 846 Faasien ja faasimuutosten termodynamiikkaa 896.1 Johdantoa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 896.2 Faasitasapaino . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 906.3 Stabiilisuus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 906.4 Faasidiagrammi ja Gibbsin faasisääntö (8.2, 8.3, 8.4) . . . . . . . 93

ivSISÄLTÖ6.5 Faasimuutoksen kertaluku . . . . . . . . . . . . . . . . . . . . . . 976.6 Vapaa energia-diagrammit (8.1) . . . . . . . . . . . . . . . . . . . 996.7 Clausiuksen ja Clapeyronin yhtälö (8.5, 8.6) . . . . . . . . . . . . 1016.7.1 Kylläisen höyryn paineen lämpötilariippuvuus . . . . . 1046.8 Faasimuutokset ja van der Waalsin tilanyhtälö (7.2, 7.3) . . . . . 1056.8.1 Van der Waalsin tilanyhtälö . . . . . . . . . . . . . . . . . 1056.8.2 Stabiilisuus ja kriittinen piste . . . . . . . . . . . . . . . . 1066.8.3 Maxwellin konstruktio . . . . . . . . . . . . . . . . . . . . 1106.8.4 Epästabiilit ja metastabiilit tilat . . . . . . . . . . . . . . . 1116.9 Pisaran tarina, osa 3: Tasapainoehdot ja muodostumisen vapaaenergia mitattavien suureiden avulla . . . . . . . . . . . . . . . . 1126.9.1 Kelvinin yhtälö . . . . . . . . . . . . . . . . . . . . . . . . 1126.9.2 Muodostumisen vapaa energia . . . . . . . . . . . . . . . 1157 Liuosten termodynamiikkaa 1217.1 Partiaaliset molekyylisuureet . . . . . . . . . . . . . . . . . . . . 1217.2 Laimeiden liuosten höyrynpaine . . . . . . . . . . . . . . . . . . 1247.3 Osmoosi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126A Termodynaamisten derivaattojen käsittelystä 128

Luku 1Johdanto1.1 Termofysiikan osa-alueetTermofysiikka on fysiikan ala, jonka avulla voidaan tutkia makroskooppistenhiukkassysteemien ominaisuuksia. Mekaniikan tai kvanttimekaniikan menetelminvoidaan tarkastella muutaman kappaleen tai hiukkasen liikettä, muttajos hiukkasia on esimerkiksi Avogadron luvun verran (6·10 23 kappaletta), eisysteemin liiketilan määrääminen käytännössä onnistu. Termofysiikan avullavoidaan laskea miten esimerkiksi paine ja tilavuus riippuvat toisistaan suuressahiukkasjoukossa tai miten nämä ominaisuudet muuttuvat kun systeemisaa tai luovuttaa energiaa. Termofysiikan menetelmä on käyttökelpoinen hyvinmonilla fysiikan aloilla annettujen oletusten rajoissa, ja siksi sitä voidaansoveltaa niin materiaalitieteessä kuin vaikkapa astro- tai aerosolifysiikassa.Termofysiikka voidaan jakaa kolmeen osa–alueeseen: tasapainotilojen termodynamiikka,tasapainotilojen tilastollinen mekaniikka ja epätasapainotilojentilastollinen mekaniikka. Tässä kirjassa tutustumme ensin tasapainotilojen termodynamiikkaan,josta jatkossa käytetään nimitystä termodynamiikka (joskuspuhutaan myös lämpöopista). Termodynamiikka on makroskooppinen teoria,joka tarkastelee aineen havaittavia termisiä ominaisuuksia perustelematta niitämikroskooppisesti. Tilastollinen (eli statistinen) mekaniikka sen sijaan ottaalähtökohdaksi aineen mikroskooppisen rakenteen.Termin termodynamiikka käyttö on hieman harhaanjohtavaa, sillä tarkkaanottaen perinteinen termodynamiikka kuvaa vain ajallisesti muuttumattomiatasapainotiloja. Tarkasteltavissa systeemeissä ja prosesseissa aikariippuvuuson usein häivytetty pois ajattelemalla, että prosessi kulkee koko ajan tasapainotilojenkautta. Toisaalta usein riittää tietää, mitkä ovat systeemin ominaisuudetmuutoksen alussa ja lopussa. Todellisia ajasta riippuvia ilmiöitä tutkiiepätasapainotilojen tilastollinen mekaniikka, mutta sitä emme tässä kirjassakäsittele: asian laajuuden lisäksi esteenä on raskaampi matemaattinen koneistokuin mitä perustermofysiikassa tarvitaan.

2 LUKU 1. JOHDANTO1.2 Termodynamiikan käsitteistöä (1.3)Aluksi määrittelemme muutamia termodynamiikan peruskäsitteitä, jotka ovatvälttämättömiä seuraavien kappaleiden ymmärtämiseksi. Eräitä termistenprosessien luonteeseen liittyviä käsitteitä otetaan esille myöhemmin.Systeemi eli järjestelmä on tarkasteltavaksi valittu fysikaalinen kokonaisuus.Systeemin ulkopuolelle jää ympäristö. Vuorovaikutus ympäristön kanssamäärää systeemin luonteen:• Avoin systeemi vaihtaa ympäristön kanssa sekä lämpöä että ainetta.• Suljettu systeemi on lämmönvaihdossa ympäristön kanssa, mutta systeeminhiukkasmäärä pysyy vakiona.• Lämpöeristetyn systeemin ja ympäristön välillä ei ole lämmönvaihtoa (eikähiukkasvaihtoa), mutta energiaa voi siirtyä systeemiin tai systeemistätyön (katso luku 3.1) muodossa• Eristetyn systeemin ja ympäristön välillä ei esiinny mikäänlaista energianeikä hiukkasten vaihtoa.Termodynaaminen tasapainotila on aineen tila, jossa ei tapahdu mitään makroskooppisiamuutoksia tai virtauksia. Termodynaamista tasapainotilaa karakterisoivattilamuuttujat, joita ovat esimerkiksi paine P, lämpötila T, tilavuuus V jamagneettikentän voimakkuus H. Osaa muuttujista voidaan kutsua tilanfunktioiksi.Ajatus tässä on se, että on joukko muuttujia, jotka kyseisessä tilanteessatiedetään eli voidaan mitata, ja näistä voidaan laskea yksikäsitteisiä tilalleominaisia tilafunktioita, joita ei ainakaan kyseisessä tilanteessa suoraan mitata.Sama muuttuja, esimerkiksi paine, voi olla toisessa tilanteessa tilamuuttujanluontoinen, ja toisessa tilanfunktion luontoinen. Tilamuuttujat jaetaan ekstensiivisiinja intensiivisiin muuttujiin.• Ekstensiiviset muuttujat ovat verrannollisia systeemin hiukkasmäärään(tai moolimäärään) tai tilavuuteen. Ekstensiivisiä muuttujia ovat esimerkiksihiukkasluku N, tilavuus V, entropia S ja kaikki energiasuureet.• Intensiiviset muuttujat eivät riipu aineen määrästä, ne ovat paikallisiaominaisuuksia. Intensiivisiä muuttujia ovat mm. lämpötila T, paine P jalukumäärätiheys ρ = N/V.Termodynaamisissa lausekkeissa tilamuuttujat esiintyvät konjugoituina pareina.Ekstensiivistä suuretta tai sen differentiaalia kuvaavassa lausekkeessatoinen konjugoiduista muuttujista on aina ekstensiivinen ja toinen intensiivinen(esimerkiksi PdV tai TS).Termodynaamisella rajalla hiukkasmäärä N → ∞ ja systeemin tilavuusV → ∞ lukumäärätiheyden N/V pysyessä vakiona. Termodynamiikan tuloksetovat tarkkaan ottaen voimassa vain termodynaamisella rajalla.

1.3. IDEAALIKAASUN TILANYHTÄLÖ (1.2, 1.4) 3Tilanyhtälö antaa tilamuuttujien keskinäisen riippuvuuden tasapainotilassa.Yleisesti tilanyhtälö on muotoaf(X i ) = 0,missä joukko X i koostuu k:sta systeemiä kuvaavasta tilamuuttujasta, joistak − 1 kappaletta on toisistaan riippumattomia. Yleensä tilanyhtälössä esiintyyvain helposti mitattavia suureita, kuten paine, lämpötila, magneettikentänvoimakkuus jne. Jos paine, lämpötila ja tilavuus määräävät yksikäsitteisestisysteemin tilan, puhutaan PTV-systeemistä. Tilanyhtälö on silloin yleisestif(P, T, V) = 0. Usein se annetaan muodossaP = P(T, V).Jatkossa käytämme PTV-systeemiä prototyyppinä esitellessämme termodynamiikanlakeja ja menetelmiä. Seuraavassa luvussa tutustumme kaikkeintunnetuimpaan PTV-systeemin tilanyhtälöön, ideaalikaasun tilanyhtälöön.Otamme esimerkkejä myös muista tilanyhtälöistä.1.3 Ideaalikaasun tilanyhtälö (1.2, 1.4)Ensimmäisen kaasujen käyttäytymistä kuvaavan yhtälön julkaisi Robert Boyle(1627–1691) vuonna 1660. Boyle huomasi, että vakiolämpötilassa kaasun tilavuusV on kääntäen verrannollinen sen paineeseen P:V = f 1 (T)/P tai PV = f 1 (T), (1.1)missä f 1 (T) on jokin lämpötilan funktio, eli vakio lämpötilan ollessa vakio.Myöhemmin Jacques Charles (1746–1823) havaitsi, että vakiopaineessa tilavuuson suoraan verrannollinen lämpötilaan:V = f 2 (P)T tai V/T = f 2 (P) (1.2)missä f 2 (P) on paineen funktio. Joseph Louis Gay-Lussac (1778–1850) havaitsi,että tilavuuden ollessa vakio paine on suoraan verrannollinen lämpötilaanP = f 3 (V)T tai P/T = f 3 (V) (1.3)Kaikissa kolmessa edellisessä yhtälössä ainemäärä on pidetty vakiona. Vuonna1811 Amadeo Avogadro (1776–1856) esitti hypoteesin, jonka mukaan vakiopaineessaja -lämpötilassa kaasun tilavuus on verrannollinen ainemäärään n:V = f 4 (T, P)n tai V/n = f 4 (T, P). (1.4)Yhdistämällä tulokset (1.1), (1.2) ja (1.4) päätellään, ettäPV = nRT, (1.5)

4 LUKU 1. JOHDANTOmissä verrannollisuuskerroin R = 8, 314 J/(mol K) on yleinen kaasuvakio , jotakutsutaan myös mooliseksi kaasuvakioksi. Ainemäärän n yksikkö on mol jan = N/N A , missä N A = 6, 022· 10 23 mol −1 on Avogadron luku. Avogadronluku on atomien määrä 12 grammassa hiili 12 alkuainetta, ja se on valittu näinkoska tämän alkuaineen atomipaino voitiin määritellä erityisen tarkasti. Yhtälö(1.5) on klassisen ideaalikaasun tilanyhtälö.Ideaalikaasun tilanyhtälö voidaan johtaa yksinkertaisen kineettisen tarkastelunavulla. Teemme seuraavat oletukset:• Kaasu koostuu identtisistä molekyyleistä, joiden massa on m.• Molekyylejä on paljon, ts. kaasua on makroskooppinen määrä.• Molekyylien välillä ei ole vuorovaikutuksia.• Törmäykset pintoihin ovat kimmoisia, jolloin liike-energia törmäyksissäsäilyy.Todellisten molekyylien välillä on aina vuorovaikutuksia, mutta niiden huomiottajättäminen on perusteltua, jos vuorovaikutusten kantama on lyhyt ja joskaasu on harvaa. Usein ideaalikaasumolekyylejä luonnehditaan infinitesimaalisenpieninä massapisteinä, jolloin myöskään molekyylien väliset törmäykseteivät ole mahdollisia. Termodynamiikan kannalta tämä vaatimus on huono,koska kaasun termalisoituminen eli tasapainon saavuttaminen ei ole mahdollistatörmäysten kautta. Seuraavassa tällä määritelmäerolla ei ole merkitystä,koska oletamme vuorovaikutuksen vain idealisoidun kiinteän seinän ja kaasunvälillä.Tarkastellaan molekyylejä kuutiossa, jonka särmän pituus on L. Olkoonmolekyylin i nopeus x-suunnassa v x,i . Molekyyli törmää silloin yhteen seinäänv x,i /2L kertaa aikayksikössä, kun oletetaan, että törmäykset seinään ovatkimmoisia ja molekyyli ei törmää toisiin molekyyleihin. Seinään kohdistuutörmäyksestä impulssi (yhtä kuin molekyylin liikemäärän muutos)∆p x,i = 2mv x,i .Koska törmäystaajuus on v x,i /2L ja Newtonin toisen lain mukaan voima onF = ∆p/∆t, on kaikista molekyyleistä tarkasteltavaan seinään kohdistuva kokonaisvoimaF =N 2mv 2 x,i∑ =2Li=1N mv 2 x,i∑L ,i=1missä N on molekyylien lukumäärä. Toisaalta paine on voimaa pintaalayksikköäkohden, jotenP = F L 2 = N∑i=1mv 2 x,iL 3 .Koska V = L 3 , saadaanP = m VN∑ v 2 x,i . (1.6)i=1

1.3. IDEAALIKAASUN TILANYHTÄLÖ (1.2, 1.4) 5Nopeuden neliön keskiarvo onv 2 = 1 NN∑i=1(v 2 x,i + v2 y,i + v2 z,i ).Voidaan olettaa, että nopeusjakauma on isotrooppinen, jolloinv 2 x = 1 NN∑ v 2 x,i = 1 Ni=1N∑ v 2 y,i = 1 Ni=1N∑ v 2 z,i = 1 3 v2 .i=1Sijoittamalla tämä tulos paineen lausekkeeseen (1.6) saadaanP = m V · 13 Nv2 .Systeemin (translaatioliikkeeseen liittyvä) kineettinen energia onjolloin paineeksi saadaanU trans = 1 2 Nmv2 ,P = 2U trans3V . (1.7)Määritellään kineettinen lämpötila molekyylin kokonais liike-energiana kerrottunavakiolla ja jaettuna molekyylin efektiivisten liikevapausasteiden lukumäärälläf :UT kin = vakio·f N . (1.8)Edellisen yhtälön vakio on 2/k B , missä k B on Boltzmannin vakio,k B = 1, 380658· 10 −23 J/K.Vapausasteiden lukumäärä tarkasteltaville rakenteettomille yksiatomisille ideaalikaasumolekyyleilleon f = 3, koska molekyyleillä voi olla vain etenevääeli translaatioliikettä. Molekyylin liikkeen kuvaamiseen riittää kolme paikkakoordinaattia.Kaksiatominen molekyyli voi myös pyöriä, jolloin molekyylinorientaation määrittelemiseksi tarvitaan kaksi kulmamuuttujaa. Kaksitomisillemolekyyleille on siis f = 5 (3 translaatio- ja 2 rotaatiovapausastetta). Jos molekyyliltäpuuttuu symmetria-akseli, kuten moniatomisilta ei-lineaarisilla molekyyleiltä,tarvitaan vielä yksi kulmamuuttuja lisää ja f = 6 (3 translaatio- ja3 rotaatiovapausastetta). 1Termodynaamisessa tasapainossa kineettinen lämpötila voidaan samaistaamyöhemmin määriteltävän absoluuttisen lämpötilan T kanssa. Samoin mekaaninenpaine samaistuu termodynaamiseen paineeseen vain tasapainotilassa. Absoluuttistalämpötilaa mitataan kelvineinä (asteikkoväli sama kuin celsiusasteikolla)ja absoluuttisen lämpötila-asteikon nollakohta on -273.15 °C. Absoluuttistalämpötila-asteikkoa käsitellään tarkemmin Carnot’n koneen yhteydessäkappaleessa 4.2.1 Reaalikaasuille f = f(T, P) johtuen sisäisistä vapausasteista (värähtely), molekyylien välisistävuorovaikutuksista ja kvanttimekaanisista ilmiöistä.

6 LUKU 1. JOHDANTOYhtälöstä (1.8) saadaan ideaalikaasun energiaksiU = f 2 k BNT, (1.9)josta translaation osuus on (ja yksiatomiselle ideaalikaasulle koko kineettinenenergia)U trans = 3 2 k BNT. (1.10)Kun tämä sijoitetaan paineen lausekkeeseen (1.7) saadaan tulokseksi ideaalikaasuntilanyhtälö:PV = k B NT. (1.11)Vertaamalla yhtälöitä (1.5) ja (1.11) saadaan vakioiden k B , N A ja R välille relaatiok B N A = R. (1.12)On syytä huomata, että yhtälöä (1.9) ei saa sijoittaa yhtälöön (1.7), koskaideaalikaasun paineeseen lasketaan kontribuutio vain molekyylien etenevästäeli translaatioliikkeestä. Ideaalikaasun tilanyhtälö pätee myös moniatomisillemolekyyleille, kunhan vain alussa mainitut ehdot ovat voimassa.1.4 Esimerkkejä tilanyhtälöistä (1.5, 7.2)1.4.1 Reaalikaasun viriaalikehitelmäReaalikaasun molekyylien väliset vuorovaikutukset voidaan ottaa huomioonkehittämällä paine lukumäärätiheyden ρ = N/V potenssisarjaksi:P = k B T[ρ+ρ 2 B 2 (T)+ρ 3 B 3 (T)+...], (1.13)missä viriaalikertoimet B i (T) ovat lämpötilan funktioita. Viriaalikertoimet voidaan(ainakin periaatteessa) laskea, kun molekyylien välinen vuorovaikutuspotentiaalitunnetaan.1.4.2 Van der Waalsin tilanyhtälöReaalisia vuorovaikuttavia kaasuja voidaan kuvata kvalitatiivisesti van derWaalsin yhtälöllä(P+ av 2)(v−b) = k BT, (1.14)joka voidaan kirjoittaa myös muotoonP = k BTv−b − a v 2 , (1.15)

1.4. ESIMERKKEJÄ TILANYHTÄLÖISTÄ (1.5, 7.2) 7missä v = V/N on molekyylitilavuus. Kertoimet a ja b ovat semiempiirisiäainevakioita. On huomattava, että mikäli a ja b on annettu yksiköissä jotkasisältävät moolin, esimerkiksi [a] = l 2 bar/mol 2 ja [b] = l/mol, on joko nämävakiot muunnettava Avogadron lukua N A käyttäen per molekyyli -muotoon,tai vaihtoehtoisesti on van der Waalsin tilanyhtälössä käytettävä molekyylitilavuudenv sijasta moolitilavuutta v n = V/n (missä n = N/N A ) ja Boltzmanninvakion k B sijasta moolista kaasuvakiota R = k b N A .Kerroin a liittyy molekyylien väliseen attraktiiviseen vuorovaikutukseen(todennäköisyys, että, molekyylit ovat niin lähellä toisiaan, että ne vetävät toisiaanmerkittävästi puoleensa on verrannollinen lausekkeeseen 1/v 2 ) ja kerroinb on pienin mahdollinen tilavuus per molekyyli, eli molekyylin “koko”.Van der Waalsin tilanyhtälö pystyy kuvaamaan nesteen ja kaasun välisen faasimuutoksen(katso luku 6.8).1.4.3 Curien lakiTermofysiikan käyttökelpoisuus ei rajoitu vain systeemeihin, joita kuvaavat tilamuuttujatP, T ja V, ja joilla on kaasu- ja nestefaasit ja mahdollisesti useampikiinteä faasi. Esimerkkinä otamme magneettiset systeemit.Ulkoiseen kenttään asetetun aineen magneettivuon tiheys on ilmaistavissamuodossaB = µ 0 (H+M), (1.16)missä H on magneettikentän voimakkuus, M on magneettinen polaroituma elimagnetoituma (magneettinen kokonaismomentti tilavuusyksikköä kohden) jaµ 0 on tyhjiön permeabiliteetti (= 4π· 10 −7 Vs/Am).Paramagneettisen aineen atomeilla on pysyvät dipolimomentit. Heikossaulkoisessa kentässä lämpöliike estää dipolien järjestäytymisen, mutta vahvassakentässä dipolit järjestyvät kentän suuntaisiksi. Jos vain pieni osa atomeistaon järjestäytyneitä, magneettisen polaroituman ja ulkoisen kentän välinen riippuvuussaadaan Curien laistaM = DN H, (1.17)VTmissä D on ainevakio. Curien laki vastaa PVT-systeemien ideaalikaasulakia.Ferromagneettisissa aineissa on pysyvä magneettinen järjestys. Jos ferromagneettistaainetta kuumennetaan tarpeeksi muuttuu aine paramagneettiseksins. Curien lämpötilassa.

Luku 2Termodynamiikan nollaspääsääntöTermodynamiikka perustuu neljään pääsääntöön, jotka ovat yhtä keskeisessäasemassa kuin Newtonin lait mekaniikassa. 1 Termodynamiikan pääsäännöt(0–3) ovat luonnonlakeja, joita ei voi johtaa muista tuloksista.2.1 Termodynaaminen tasapaino (1.3)Termodynamiikan nollanneksi pääsäännöksi voidaan kutsua seuraavaa havaintoa:Jos kaksi systeemiä ovat erikseen termodynaamisessa tasapainossakolmannen kanssa, niin ne ovat tasapainossa myös keskenään:tasapaino1 3∧tasapaino2 3⇒tasapaino1 2Nollannesta pääsäännöstä seuraa, että on olemassa tilamuuttuja, joka kuvaatermisessä kosketuksessa olevien systeemien tasapainoa. Tämä tilamuuttujaon lämpötila: jos kaksi systeemiä on termodynaamisessa tasapainossa, niidenlämpötilat ovat samat. Lämpötilavertailun transitiivisuudesta seuraa lisäksi,että voidaan valita jokin referenssisysteemi, jota käytetään lämpötilan mittaamiseen,toisin sanoen se toimii lämpömittarina. Jo James Clerk Maxwell (1831–1879) tunsi tämän periaatteen mutta vasta Fowler ja Guggenheim (1939) ehdottivatnimeä “nollas pääsääntö”. Lyhyenä muistisääntönä nollas pääsääntö voikuulua vaikkapa seuraavasti: Lämpötilan käsite on hyvin määritelty ja on olemassalämpömittari.Havainnollistamme lämpötilan käsitettä yksinkertaisella PTV-systeemillä,joka koostuu eristetystä (eli jäykkäseinäisestä, ainetta ja lämpöä läpäisemättömästä)1 Historiallisista syistä suomenkielisessä kirjallisuudessa puhutaan termodynamiiikanpääsäännöistä, ei laeista.

2.2. LÄMPÖMITTARIT JA LÄMPÖTILA-ASTEIKOT (1.2) 912P 1V 1P 2V 2Kuva 2.1: Diatermisellä seinällä kahteen osaan jaettu laatikko.laatikosta, joka on jaettu kahteen osaan diatermisellä eli lämpöä läpäisevälläseinällä (kuva 2.1). Termodynaamisessa tasapainossa molempien systeemien1 ja 2 tilanyhtälöt θ i = f i (P i , V i ), i = 1, 2 saavat saman lukuarvon:f 1 (P 1 , V 1 ) = f 2 (P 2 , V 2 ) = θ,missä θ on empiirinen lämpötila. Tämä tarkoittaa että systeemiä 2 voidaankäyttää lämpömittarina mitattaessa systeemin 1 lämpötilaa tai päinvastoin.2.2 Lämpömittarit ja lämpötila-asteikot (1.2)Esimerkkinä lämpömittareista tarkastelemme kuvan 2.2 kaltaista kaasulämpömittaria.Putken harmaa osa on täytetty elohopealla, ja pallossa on kaasua. Elohopeanmäärää tai käytännössä yleensä putken asentoa säädellään niin, ettäkaasun ja elohopean rajapinta pysyy aina samassa kohdassa eli kaasun tilavuuson vakio. Oletetaan, että mitattavana on erään fluidin (nesteen tai kaasun)lämpötila. Mittarissa olevan kaasun paine saadaan hydrostaattisen tasapainonyhtälöstäP = ρ m g∆h,missä ρ m on elohopean massatiheys, k on painovoimavakio ja ∆h on elohopeapatsaidenpäiden korkeusero. Mittaus antaa paineen mutta ei lämpötilaa.∆hPKuva 2.2: Kaasulämpömittarin periaatekuva.

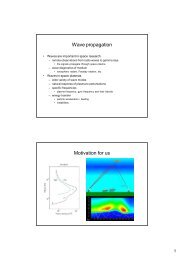
10 LUKU 2. TERMODYNAMIIKAN NOLLAS PÄÄSÄÄNTÖθ374.00373.75373.50373.25373.00O 2IlmaN 2H 20 250 500 750 1000P 0 (mmHg)Kuva 2.3: Tiivistyvän vesihöyryn (P = 1 atm) lämpötila kaasulämpömittarillamitattuna eri P 0 :n arvoilla ja erilaisilla kaasuilla.Tiedämme kuitenkin, että jos mittarin kaasu on harvaa, noudattaa se Boylenlakia PV = vakio, missä V on kaasun tilavuus ja vakio riippuu empiirisestälämpötilasta θ, ts. PV = f(θ). Mitataan nyt vertailuarvoksi jonkin referenssifluidinaiheuttama paine P 0 siten, että elohopean rajapinta pidetään samassakohdassa eli kaasun tilavuus on sama. Voimme muodostaa verrannonP= f(θ)P 0 f(θ 0 ) ,missä θ 0 on referenssifluidin lämpötila. Jotta ideaalikaasun tilanyhtälösäilyttäisi tutun funktionaalisen muotonsa, on järkevää valita lämpötilaasteikkolineaariseksi eli f(θ) = vakio×θ. Nyt empiiriseksi lämpötilaksi saadaanθ = θ 0PP 0.Seuraavaksi otetaan mittarin kaasusta osa pois, jolloin paine on pienempi, jasuoritetaan uudet mittaukset. Jatkamalla mittauksia yhä pienemmillä paineillaja ekstrapoloimalla rajalle P 0 → 0 (samalla menee myös P → 0) havaitaan, ettäriippumatta mittarissa käytetystä kaasusta saadaan sama lämpötila θ (katsokuva 2.3). Sen vuoksi on mahdollista määritellä ideaalikaasulämpötilaPθ = θ 0 lim (V = vakio). (2.1)P0 →0 P 0Kun vielä referenssilämpötilaksi θ 0 valitaan veden kolmoispisteen lämpötila javalitaan tälle lukuarvo 273,16 K, antaa yhtälö (2.1) lämpötilan kelvinasteissa.Palaamme kysymykseen absoluuttisen lämpötila-asteikon määrittelemisestäkappaleissa 4.2 ja 4.4.Lämpömittari voi perustua myös metallien sähköisiin ominaisuuksiin.Lämpösähköparissa kahden eri metallijohtimen liitoskohtaan syntyy lämpötilastariippuva jännite. Termistori taas on vastus, jonka resistanssi riippuulämpötilasta. Myös kappaleen säteily kertoo sen lämpötilan. Arkipäivän

2.2. LÄMPÖMITTARIT JA LÄMPÖTILA-ASTEIKOT (1.2) 11lämpömittarit perustuvat tavallisimmin lämpölaajenemiseen. Tällaisia ovatnestelämpömittarit ja kaksoismetallilämpömittarit.Tutuin lämpötila-asteikko on Celsius-asteikko, joka määritellään siten, ettäveden kolmoispiste on 0,01°C. Silloin celsiuslämpötila t celsius saadaan kelvinlämpötilastaT muunnoskaavallat celsius = T− 273, 15°C.Veden jäätymispiste celsiusasteikolla on 0°C ja kiehumispiste 100°C. Celsiusjakelvinasteikkojen asteväli on sama.Yhdysvalloissa on vielä yleisesti käytössä fahrenheitasteikko, jolla vedenjäätymispiste on 32 °F ja kiehumispiste 212 °F. Muunnoskaava ont celsius = 5 9 (t fahrenheit− 32).Näiden lisäksi on lukuisa määrä jo käytöstä poistettuja lämpötila-asteikkoja.

Luku 3Termodynamiikanensimmäinen pääsääntö3.1 Työ (2.2, 2.7)Termodynamiikassa systeemi ja ympäristö voivat vaihtaa energiaa työn,lämmön tai hiukkasmäärän muutoksiin liittyvän energian muodossa. Työ voiolla esimerkiksi tilavuudenmuutostyötä, joka on tavallisimmin termofysiikanesimerkeissä esiintyvä työn laji. Klassisen mekaniikan differentiaalinen työ d¯Wond¯W = F·ds,missä F on voima ja s on siirtymä. Merkintä d¯W tarkoittaa että tehty työ riippuusiitä miten siirros on tehty, eikä sitä voida laskea yksistään alku- ja lopputilojenavulla. Työn differentiaali on silloin epäeksakti (katso kappale 3.2).Tarkastellaan esimerkkinä sylinterin ja männän muodostamaa systeemiä(kuva 3.1). Kaasun tilavuuden muuttuessa määrän dV siirtyy mäntä (pintaalaA) matkan dL. Tutkitaan ulkoista mäntää liikuttavaa voimaa, joka tekeemäntään työn, jonka itseisarvo on |F · dL|. Työn merkki määritellään si-PAdL, FKuva 3.1: Sylinteri-mäntä systeemi.

3.1. TYÖ (2.2, 2.7) 13ten, että jos kaasuun tehdään työtä, työ on negatiivista, jos taas kaasu tekeeympäristöön työtä, työ on positiivista. Voiman suuruus voidaan lausua paineenavulla, sillä se on mekaniikassa määritelty voimana per pinta-ala yksikköP ulkoinen = F/A ja kun vielä huomataan, että tässä järjestelyssä voima F ja siirtymädL ovat yhdensuuntaiset, ja AdL on kaasun tilavuuden muutos, saadaantehdyksi työksid¯W = P ulkoinen AdL = P ulkoinen dV. (3.1)Tilavuudenmuutostyö on nyt lausuttu ulkoiseen voimaan liittyvän paineenP ulkoinen avulla, mutta millä ehdoilla tämä paine on sama kuin kaasun paine P?Kaasun paineesta on mielekästä puhua vain silloin, kun tilamuuttujat ovathyvin määritellyt eli kun systeemi on termodynaamisessa tasapainossa taikäytännössä hyvin lähellä tasapainoa. Voidaksemme käyttää yhtälön (3.1) kaltaisiatyön lausekkeita termodynaamisten muutosten eli prosessien kuvaamiseenmäärittelemme kvasistaattisen prosessin:Kvasistaattinen prosessi tapahtuu niin hitaasti, että systeemin tilaon jokaisena ajanhetkenä mielivaltaisen lähellä tasapainotilaa.Kvasistaattista prosessia kuvaa hyvin määritelty polku tilamuuttuja-avaruudessa.Esimerkiksi kaasun äkillinen laajeneminen vaikkapa kaksinkertaiseentilavuuteen ei ole kvasistaattinen prosessi, eikä tasapainotermodynamiikankeinoin voida tehdä päätelmiä systeemin tilasta prosessin aikana. Sen sijaanprosessin päätepisteissä tilamuuttujat ovat hyvin määritellyt ja esimerkiksi aineentilanyhtälö on voimassa.Männän äärimmäisen hidas liike vaatii sitä, että mäntään vaikuttava kokonaisvoimaon (lähes) nolla. Tällöin kaasun paine on hyvin määritelty, ja se kohdistaamäntään ulospäin työntävän voiman PA ≡ P kaasu A, jonka tulee siis ollayhtäsuuri kuin mäntää sisäänpäin työntävä ulkoinen voima P ulkoinen A. Kvasistattiseessatapauksessa työn lauseke voidaan kirjoittaa kaasun paineen avullad¯W = P kaasu dV ≡ PdV. (3.2)Yhtälö (3.2) on yleinen tilavuudenmuutostyön lauseke, eikä se riipu systeeminmuodosta.Jos prosessi on kvasistaattinen, voidaan tilavuudenmuutostyö (tai vastaavastimikä tahansa työ) laskea integroimalla työn lauseke (3.2) prosessin alkupisteestäsen loppupisteeseen:(∆W ab ) kv.stat. =∫ VbV aPdV (3.3)Tehty työ(P, V)-tasossa on tällöin kuvan 3.2 mukaisesti painekäyrän alle jääväpinta-ala. Vaikka systeemin termodynaaminen tila olisikin hyvin määriteltyprosessin aikana, riippuu tehty työ silti prosessin luonteesta (katso kappale3.5). Jos prosessi ei ole kvasitaattinen, on selvitettävä ulkoiset voimat, ja työnlaskemisessa on turvauduttava muotoon (3.1).

14 LUKU 3. TERMODYNAMIIKAN ENSIMMÄINEN PÄÄSÄÄNTÖPV aV bVKuva 3.2: Painekäyrän alle jäävä varjostettu alue (P, V)-tasossa on tehty tilavuudenmuutostyö.Systeemi voi tehdä myös muuta kuin tilavuudenmuutostyötä. Venytettäessäesimerkiksi sauvaa, voidaan kimmoinen muodonmuutostyö lausua differentiaalisessamuodossad¯W = −FdL, (3.4)missä F on sauvaa venyttävä voima ja n on venymä. Hooken lain mukaanjännitys eli voima poikkipinta-alayksikköä kohden on lausuttavissa muodossaFA = E L−L 0L 0,missä E on kimmokerroin ja L 0 on sauvan lepopituus. Miinus-merkki lausekkeessa(3.4) johtuu siitä, että positiivisen muutoksen L−L 0 aikaansaamiseksiympäristön on tehtävä työtä sauvaan.Nesteen ja kaasun rajapintaan liittyy pintaenergia. Pintaenergian muutoksistaaiheutuu työd¯W = −σdA, (3.5)missä A on pinta-ala ja σ on pintajännitys. Pintajännityksen kuvaama energiaaiheutuu siitä, että nesteen pinnalla olevat molekyylit ovat erilaisessa asemassakuin nesteen sisällä: ne eivät pysty asemoitumaan siten, että niiden sidosverkkoympäröiviin molekyyleihin olisi energeettisesti mahdollisimman edullinen.Pinnalla olevan molekyylin keskimääräinen energia on täten suurempikuin nesteen sisällä olevan, ja pinnan muodostaminen vaatii energiaa, eli pintaamuodostettaessa täytyy tehdä työtä.Magneettinen työ voidaan lausua muodossad¯W = −µ 0 V H·dM (3.6)Tässä miinus-merkki johtuu siitä, että magneettinen polaroituma M aiheutuuulkoisesta kentästä H. 1 Vastaavuudet PTV-systeemin kanssa ovat P ↔ −H jaV ↔ µ 0 VM.1 Yhtälö (3.6) sopii käytettäväksi tavanomaisille magneettisille materiaaleille, joissa ulkoinenkenttä H vallitsee niin kappaleen ulkopuolella kuin sen sisälläkin. Jos kentän tunkeutuminenaineeseen on kokonaan tai osittain estynyt, kuten on esimerkiksi suprajohteissa, on työllejärkevämpää käyttää muotoa d¯W = −V H·dB.

3.2. EKSAKTIT JA EPÄEKSAKTIT DIFFERENTIAALIT (3.1) 153.2 Eksaktit ja epäeksaktit differentiaalit (3.1)Tarkastellaan kahden muuttujan funktiotaz = z(x, y), (3.7)joka oletetaan jatkuvaksi ja derivoituvaksi. Osittaisderivaattoja laskettaessa ontermodynamiikassa tapana merkitä vakioina pidettävät muuttujat derivaattamerkinnänoikeaan alakulmaan:( ∂z∂x)ykun y on vakio,( ) ∂z∂yxkun x on vakio.Jos siirrytään pisteestä(x, y) pisteeseen(x+dx, y+dy) ilmaisee z:n muutoksenkokonaisdifferentiaali:( ) ( )∂z ∂zdz = dx+ dy. (3.8)∂x y ∂yxEsimerkki 3.1Lasketaan ensimmäiset ja toiset derivaatat kahden muuttujanfunktiollez = 1 + xy+ln y.xEnsimmäiset derivaatat ovat( ) ∂z= − 1 ( ) ∂z∂x y x 2 + y, = x+ 1 ∂yxyja toiset[ ( )]∂ ∂z∂x ∂x y y[ ( )]∂ ∂z∂x ∂yxy= ∂2 z∂x 2 = 2 x 3= ∂2 z∂x∂y = ∂∂x(x+ 1 )= 1.yEsimerkki 3.2Ideaalikaasun tilanyhtälöstä PV = k B NT ratkaistaanV = k BNTP= V(T, P).Tilavuuden kokonaisdifferentiaali ideaalikaasulle on( ) ( )∂V ∂VdV = dT+ dP = k BN∂T ∂P PdT− k BNTP 2 dP.PT

16 LUKU 3. TERMODYNAMIIKAN ENSIMMÄINEN PÄÄSÄÄNTÖSamalla tavalla voidaan lausua kokonaisdifferentiaalit dP(T, V) jadT(P, V).LausekettaAdx+ Bdy+Cdz+... (3.9)sanotaan Pfaffin differentiaalimuodoksi. Kertoimet A(x, y, z, ...), B(x, y, z, ...) jne.ovat muuttujien x, y, z, ... analyyttisiä funktioita. Lauseke (3.9) ei välttämättäole minkään funktion kokonaisdifferentiaali. Jos Pfaffin differentiaalimuoto onjonkin funktion F kokonaisdifferentiaali, kirjoitetaandF = Adx+ Bdy+Cdz+... (3.10)ja sanotaan, että dF on eksakti differentiaali. Muussa tapauksessa differentiaalion epäeksakti ja merkitäänd¯F = Adx+ Bdy+Cdz+... (3.11)Koska differentiaali on eksakti? Asian selvittämiseksi tarkastellaan kahdenmuuttujan tapausta. Verrataan muotoja( ) ( )∂F ∂FdF = dx+ dy∂x y ∂yxjad¯F = Adx+Bdy,joista edellinen muoto on kokonaisdifferentiaali ja siis eksakti. Jotta jälkimmäinenmuoto olisi myös eksakti on ainakin oltava voimassa( ) ( )∂F∂FA = ja B =∂x∂yLisäksi derivaatan arvo ei saa riippua derivointijärjestyksestä, ts.y.x∂ ∂F∂y ∂x = ∂2 F∂y∂x = ∂2 F∂x∂y = ∂ ∂F∂x ∂y .Differentiaali on siten eksakti, kun voimassa on ns. resiprookkisuusehto∂A(x, y)∂yJos muuttujia on kolme, on eksaktille differentiaalillevoimassa yhtäaikaiset ehdot∂A∂y = ∂B∂x=∂B(x, y). (3.12)∂xdF = Adx+ Bdy+Cdz (3.13);∂A∂z = ∂C∂x;∂B∂z = ∂C∂y . (3.14)

3.2. EKSAKTIT JA EPÄEKSAKTIT DIFFERENTIAALIT (3.1) 17Esimerkki 3.3Onko differentiaalixdy+ydxeksakti? Lasketaan yhtälön (3.12) derivaatat:∂x∂x = 1 = ∂y∂y .Differentiaali on siis resiprookkisuusehdon nojalla eksakti. Helpostitodetaan, ettäxdy+ydx = d(xy).Esimerkki 3.4Onko differentiaalixdy−ydx.eksakti? Resiprookkisuusehdosta saadaan∂x∂(−y)= 1 ̸= −1 =∂x ∂y .Differentiaali on epäeksakti. Tässä tapauksessa ei ole olemassafunktiota f(x, y), jonka differentiaali d f(x, y) olisi xdy−ydx.Esimerkki 3.5Löytyykö lämpötilan ja paineen funktiota, jonka differentiaali olisik B NPdT− k BNTP 2 dP ?Välittömästi todetaan∂(k B N/P)∂P= −k BNP 2 = ∂(−k BNT/P 2 ).∂TKyseessä on tilavuuden differentiaali dV(T, P) ideaalikaasusysteemissä(esimerkki 3.2), joka on siis eksakti kuten pitääkin.Jos dF on eksakti, voidaan osoittaa, että voimassa ovat myös seuraavatväitteet:

18 LUKU 3. TERMODYNAMIIKAN ENSIMMÄINEN PÄÄSÄÄNTÖa) IntegraalinF(b)− F(a) =∫ badF =∫ ba[A(x, y)dx+ B(x, y)dy]arvo ei riipu integrointireitistä pisteiden a ja b välillä. (Vrt. mekaniikkaan:konservatiivisten voimien tekemä työ on tiestä riippumaton.)b) Suljettua integrointireittiä pitkin∮ ∮dF = [A(x, y)dx+ B(x, y)dy] = 0.c) Jos dF tunnetaan, voidaan F määrittää vakiota vaille.Väittämän (c) perusteella on selvää, että termodynaamisen tilamuuttujandifferentiaalin tulee olla eksakti, muutoinhan tätä tilamuuttujaa ei edes olisiolemassa! Kohta (a) taas kertoo, että tilamuuttujan muutoksen laskemiseksiriittää tietää muuttujan arvot prosessin päätepisteissä. Tästä on paljon hyötyäanalysoitaessa termodynaamisia muutoksia.Voidaanko epäeksakti differentiaali muuntaa eksaktiksi? Kahden muuttujantapauksessa on aina löydettävissä ns. integroiva tekijä λ(x, y) siten, ettäλd¯F = λAdx+λBdy = d fon eksakti differentiaali. Epäeksakti differentiaali voidaan siis lausua eksaktindifferentiaalin avulla muodossad¯F = d fλ(3.15)Termodynamiikassa sekä f että λ ovat tilamuuttujia. Esimerkiksi kvasistaattisessatilavuudenmuutostyössä d¯W = PdV, missä P ja V ovat tilamuuttujia.Vertaamalla yhtälöön (3.15) nähdään, että P −1 on d¯W:n integroiva tekijä. Esimerkin3.4 epäeksaktin differentiaalin xdy−ydx integroiva tekijä on 1/x 2 .3.3 Termodynamiikanensimmäinenpääsääntö(2.3,2.1)3.3.1 Mitä lämpö on?Jo englantilaiset Robert Boyle ja Isaac Newton väittivät, että lämpö on energiaa,joka liittyy aineen mikroskooppisten osasten liikkeeseen. Sen sijaan Ranskassaoli vallalla käsitys, jonka mukaan lämpö on näkymätöntä ainetta, jota nimitettiinkalorikiksi ja joka virtasi kuumemmasta kappaleesta kylmempään. Vuonna1761 skotti Joseph Black (1728–1799) osoitti, että ämpärillinen jääkylmäävettä lämpeni nopeasti, kun se tuotiin huoneenlämpöön, mutta jos vesi sisälsijääpaloja, sen lämpötila pysyi kauan samana. Jos oletettu kalorikki virtasi

3.3. TERMODYNAMIIKAN ENSIMMÄINEN PÄÄSÄÄNTÖ (2.3, 2.1) 19ympäristöstä ämpäriin, sisälsi jääkylmä vesi siis ilmeisesti enemmän kalorikkiakuin jää. Vuonna 1799 englantilainen kemisti Humphry Davy (1778–1829)näytti, että jääpalat saatiin sulamaan hankaamalla niitä vastakkain. Kalorikkiteorianmukaan hankaaminen sai kalorikin virtaamaan jäästä ympäristöön,joten kokeen tuloksena tuotettu nestevesi sisälsi vähemmän kalorikkia kuinjää. Tällaiset ristiriitaiset havainnot saivat aikansa tutkijat epäilemään kalorikkiteoriaa,mutta vasta 1847 James Prescott Joulen (1818-1889) tutkimuksetromuttivat sen kokonaan. Kokeissaan Joule muutti vakiomäärän työtä eri tavoinlämmöksi (kitkan avulla, sähköllä lämmittämällä jne.) niin, että kaikkityö käytettiin lämmittämiseen, ja havaitsi, että tuloksena oli aina samamäärä lämpöä. Näin Joule tuli mitanneeksi lämmön mekaanisen ekvivalentin: tiettymäärä työtä tuottaa aina saman määrän lämpöä riippumatta miten muutostehdään. Joulen mittaukset osoittivat, että lämpö on energiaa siinä missätyökin.Klassisessa hiukkaskuvauksessa lämpö on eräänlaista “epäjärjestynyttä”kineettistä energiaa. Tämän lisäksi hiukkaset ovat vuorovaikutuksessa kenttienkanssa, esimerkiksi sähkömagneettisten kenttien. Kentät voivat siirtääenergiaa ja liikemäärää, ja törmäyksissä osa hiukkasten liike-energiastamuuttuu kenttien energiaksi. Kvanttikenttäteoria on osoittanut, että hiukkasetitsekin ovat vain kentän värähtelyjä ja vuorovaikutus tapahtuu ns.välittäjähiukkasten avulla. Esimerkiksi sähkömagneettisessa vuorovaikutuksessavälittäjähiukkanen on fotoni.Jo klassinen kuvaus aineesta osoittaa, että puhtaasti mekaaninen lähtökohtaon termodynaamiselta kannalta riittämätön. On täysin mahdoton ajatus, ettävoisimme rakentaa kuvauksen systeemin energian muutoksista tarkastelemallajokaisen hiukkasen energian muutoksia erikseen. Termodynamiikassa onkinjärkevää määritellä työ energiaksi, joka on täysin vaihtokelpoista muidenenergialajien kanssa. Kaikki muu energia (hiukkasmäärän pysyessä vakiona)niputetaan lämmöksi. On kuviteltavissa, että jos esimerkiksi sylinterissä laajenevakaasu tekee työtä mäntään, voidaan työ varastoida kitkattomaan jouseenja palauttaa sieltä takaisin tai muuntaa toiseen muotoon (todellinen jousi onaina kitkallinen mutta huolellisessa koejärjestelyssä kitka voidaan eliminoidalähes kokonaan). Jos sen sijaan männän tekemä työ varastoidaan lämmöksi(molekyylien liikkeeksi) vaikkapa kitkan avulla, on ilmeistä, että vain osa tästäenergiasta voidaan myöhemmin käyttää männän liikutteluun. Kappaleessa 4.1osoitamme, että lämpöä voidaan muuntaa työksi vain rajoitetusti.3.3.2 Energia säilyyTermodynamiikan ensimmäinen pääsääntö on energiansäilymislaki. Jos systeeminja ympäristön vuorovaikutus tapahtuu vain työn ja lämmönsiirronkautta, voidaan systeemin energian muutos prosessissa kirjoittaa∆U = ∆Q−∆W. (3.16)Valitussa merkkikonventiossa ∆Q on systeemiin siirtynyt lämpö ja ∆W systeeminympäristöönsä tekemä työ. Differentiaalisessa muutoksessa ylläoleva

20 LUKU 3. TERMODYNAMIIKAN ENSIMMÄINEN PÄÄSÄÄNTÖ∆QSys∆Wµ∆NKuva 3.3: Ensimmäisen pääsäännön määrittelyssä käytetyt merkkikonventiot.yhtälö saa muodondU = d¯Q−d¯W. (3.17)Termodynaamisessa kielenkäytössä systeemin kokonaisenergiaa U sanotaansisäiseksi energiaksi. Muita energiasuureita käsitellään luvussa 5.On syytä huomata, että vaikka sisäinen energia on tilamuuttuja, työ jalämpö eivät sitä ole. Koska sekä d¯W että d¯Q ovat epäeksakteja differentiaaleja,ei mitään tilamuuttujien funktioita Q ja W ole edes olemassa. Vaikka systeemilläon tietty määrä sisäistä energiaa (esimerkiksi 666 kJ), voidaan puhuavain siirtyneistä työ- tai lämpömääristä ja niiden muutoksista. Työn ja lämmöndifferentiaalien epäeksaktisuudesta seuraa myös, että∮d¯W ̸= 0ja∮d¯Q ̸= 0. (3.18)Tässä näkyy se tosiasia, että energiaa voidaan muuntaa muodosta toiseen,mikä mahdollistaa mm. lämpövoimakoneiden toiminnan.Koska U on tilamuuttuja, riippuu muutoksen ∆U arvo vain prossessinpäätepisteistä. Tärkeä termodynaaminen prosessityyppi on kiertoprosessi, eliprosessi, joka palaa tilamuuttuja-avaruudessa takaisin alkupisteeseensä. Kiertoprosessissaon voimassa∮dU = 0. (3.19)Yhtälöä (3.19) voidaan pitää eräänä ensimmäisen pääsäännön esitysmuotona.Lämpö- ja työsiirtymien ohella systeemi voi olla ympäristön kanssa hiukkasvaihdossa.Tähän liittyy J. Willard Gibbsin (1839–1903) kehittämä kemiallisenpotentiaalin käsite. Jos hiukkasvaihto on sallittu, kirjoitetaan ensimmäinenpääsääntö muodossadU = d¯Q−d¯W + µdN, (3.20)missä µ on kemiallinen potentiaali. Kemiallinen potentiaali kertoo aineenvaihdonyhteydessä systeemin siirtyvän energian hiukkasta kohden.Yhtälön (3.20) mukainen merkkikonventio on esitetty kuvassa 3.3. Muistisääntönäsille, että systeemin tekemän työn merkkisääntö on erisuuntainenkuin lämmön ja hiukkasmäärän voi ajatella hyötyä tavoittelevaa kapitalistia,jolle positiivista on systeemin (tehtaan, työläisen) ulospäin tekemä työ.

3.4. LÄMPÖKAPASITEETIT (2.5) 21Erityyppisiä kvasistaattisia töitä tekevälle ja useista hiukkaslajeista koostuvallesysteemille ensimmäinen pääsääntö voidaan ilmaista muodossadU = d¯Q−∑imissä f i on yleinen voima ja dX i yleinen siirtymä.f i · dX i + ∑ µ i dN i , (3.21)i3.4 Lämpökapasiteetit (2.5)Ensimmäisen pääsäännön avulla voidaan laskea, kuinka paljon systeemiin siirtyylämpöä:∆Q = ∆U+ ∆W.Lämpökapasiteetti kertoo kuinka paljon systeemi tarvitsee lämpöä ∆Q, jottasen lämpötila nousee määrän ∆T:( ) ∆QC ehto = lim. (3.22)∆T→0 ∆T ehtoTässä “ehto” ilmoittaa muuttujan, joka lämpökapasiteettia laskettaessa tai mitattaessapidetään vakiona.Yksinkertaiseen tilavuudenmuutostyötä tekevään PTV-systeemiin liittyvätlämpökapasiteetit ovat lämpökapasiteetti vakiotilavuudessa eli isokoorinenlämpökapasiteetti:C V = lim∆T→0( ) ∆Q∆T V(3.23)ja lämpökapasiteetti vakiopaineessa eli isobaarinen lämpökapasiteetti:( ) ∆QC P = lim . (3.24)∆T→0 ∆T PTermodynamiikan ensimmäisen pääsäännön mukaand¯Q = dU+ d¯W = dU+PdV,missä jälkimmäisessä vaiheessa muutos oletetaan kvasistaattiseksi. Silloin( ) ( )∆U ∂UC V = lim =(3.25)∆T→0 ∆T ∂TjaC P =VV( ) ( )∂U ∂V+ P . (3.26)∂T P ∂T PJälkimmäisessä yhtälössä oikean puolen toinen termi on laajentumisen aikanatehdyn työn vaikutus lämpökapasiteettiin. Isokoorisessa lämpökapasiteetissavastaavaa termiä ei ole, koska muutos tapahtuu vakiotilavuudessa.

22 LUKU 3. TERMODYNAMIIKAN ENSIMMÄINEN PÄÄSÄÄNTÖSeuraavaksi laskemme lämpökapasiteettien C P ja C V erotuksen. Tilanyhtälönmukaan f(T, P, V) = 0, eli vain kaksi muuttujista P, T ja V ovat vapaita.Voidaan siis lausua V = V(T, P) ja U = U(T, V(T, P)). Lasketaan ensin derivaatta( ) ( ∂U ∂=∂T P ∂T)PU(T, V(T, P)) =Sijoittamalla yhtälöön (3.26) saadaanC P =( ) ∂U+∂T V( ) ∂U∂V T( ) ∂U+∂T V( ) ∂V+ P∂T P( ) ∂U∂V T( ) ∂V.∂T P( ) ∂V.∂T PTässä yhtälön oikean puolen ensimmäinen termi on C V , joten saadaanlämpökapasiteettien erotusC P − C V =[( ) ]( ∂U ∂V+ P∂VT∂TIdeaalikaasulle PV = k B NT ja U = U(T), jotenja( ) ∂V= k BN∂TPP( ) ∂U= 0.∂V T). (3.27)PSijoittamalla nämä tulokset yhtälöön (3.27) saadaan lämpökapasiteettien erotukseksiideaalikaasulleC P − C V = k B N = nR, (3.28)missä jälkimmäinen muoto seuraa tuloksesta (1.12). Reaalikaasuille yhtälö (3.28)ei tarkkaan ottaen päde, koska U = U(T, V) ja (∂U/∂V) T ̸= 0.Ideaalikaasulle lämpökapasiteettien lausekkeet saadaan erityisen yksinkertaiseenmuotoon, kun muistetaan, että ideaalikaasulle U = k B TN f /2. Silloinsuoraan määritelmästä (3.25) seuraaC V = f 2 k BN (3.29)ja kaavasta (3.28)C P =( f2 + 1 )k B N. (3.30)Reaalikaasuille (ja nesteille) vapausasteiden määrä f = f(T, P), jolloin myösC V = C V (T, P).

3.5. KVASISTAATTISIA IDEAALIKAASUPROSESSEJA (˜2.1, 2.11) 23Lämpökapasiteetit C V ja C P riippuvat systeemin hiukkas- tai ainemäärästä.Jokaiselle aineelle ominainen ominaislämpökapasiteetti määritelläänc ehto = C ehtoM , (3.31)missä M on systeemin massa. Ominaislämpökapasiteettien arvoja löytyy taulukoista.Joskus on myös hyödyllistä käyttää moolista lämpökapasiteettiac m,ehto = C ehton . (3.32)Esimerkiksi yksiatomiselle ideaalikaasulle c m,V = 3R/2.Lämpökapasiteetit ovat esimerkkejä termodynaamisista vastefunktioista. Muitatermodynaamisia vastefunktioita ovat mm. tuonnempana esiteltävätlämpölaajenemiskertoimet ja kokoonpuristuvuudet.Lämpökapasiteettien välinen erotus (3.27) on ensimmäinen esimerkki tyypillisistätermodynamiikassa esiintyvistä yhteyksistä, joilla systeemiä kuvaaviaominaisuuksia voidaan laskea toisista ominaisuuksista. Jokin ominaisuusvoi olla helposti mitattava toisen mittauksen ollessa hankalaa. Tällöin hankalastimitattavan voi yhteyksien avulla laskea helpommin mitattavasta. Jos molemmatpystytään mittaamaan, säästetään vaivaa kun toinen saadaan laskemalla.Lisäksi jos molemmat mitataan pystytään arvioimaan mittauksen tarkkuuttaja/tai teoreettisen mallin sopivuutta käsiteltävään tilanteeseen sen perusteella,kuinka hyvin yhteys toteutuu.3.5 Kvasistaattisiaideaalikaasuprosesseja (˜2.1,2.11)Termodynaamista muutosta rajoittaa systeemin ja ympäristön välinen kytkentä.Jos systeemi on esimerkiksi kiinteäseinäinen, pysyy systeemin tilavuusmuutoksen aikana vakiona, ja sanomme, että muutos on isokoorinen. MuitaPTV-systeemissä tapahtuvien prosessien erikoistapauksia ovat isoterminen, isobaarinenja adiabaattinen muutos. Tässä kappaleessa esittelemme nämä prosessityypitja tutkimme, kuinka systeemin tekemä työ ja systeemiin siirtynyt lämpövoidaan laskea kvasistaattisessa tapauksessa ideaalikaasulle.3.5.1 Isoterminen prosessiIsotermisessä prosessissa lämpötila pysyy vakiona. Ideaalikaasun tilanyhtälöstäsaadaan isoterminen tilanyhtälö ideaalikaasuprosesseille:PV = vakio. (3.33)Koska ideaalikaasulle U = U(T), on ∆U = 0, kun ∆T = 0, ja ensimmäisenpääsäännön nojalla∆Q = ∆W (3.34)

24 LUKU 3. TERMODYNAMIIKAN ENSIMMÄINEN PÄÄSÄÄNTÖTP ulkV bP = k B NT/V V aKuva 3.4: Kaasun isoterminen laajeneminen männällä suljetussa sylinterissä.eli kaasun ympäristöönsä tekemä työ on täsmälleen yhtä suuri kuin kaasuunsiirtynyt lämpöenergia.Esimerkki isotermisestä prosessista on kuvan 3.4 mukainen männällä varustettuunsäiliöön suljetun ideaalikaasun laajeneminen. Mäntään kohdistuvaulkoinen paine P ulk < P eli kaasu laajenee, mutta männän massa on sopivansuuruinen, jotta laajeneminen tapahtuu hyvin hitaasti. Koska säiliö onlämmönvaihdossa ympäristön kanssa ja koska prosessi on kvasistaattinen, voidaankaasun olettaa pysyvän isotermisenä koko prosessin ajan. Kaasun tekemäkvasistaattinen työ on∫ Vb∫ VbdV∆W ab = P dV = k B NTV a V = k BNT ln V b. (3.35)V aV aTämä esimerkki valottaa myös kvasistaattisuuden merkitystä: jos mäntänostetaan nopeasti loppuasentoon, kaasun molekyylit eivät ehdi seurata tasaisestiperässä, ja paine kaikkialla säiliössä ei ole sama. Tällöin kaasun tekemääntyötä ei voi laskea integroimalla lauseketta PdV. Ääritapauksessa jos henkilönostaa männän erittäin nopeasti, kaasu säiliössä ei tee lainkaan työtä, kaikkityö on ihmisen tekemää.3.5.2 Isobaarinen prosessiIsobaarisessa prosessissa paine on vakio. Ideaalikaasun tilanyhtälön nojallaisobaarinen tilanyhtälö onV= vakio. (3.36)TIsobaarisessa prosessissa sekä tehty työ että siirtynyt lämpö voivat olla nollastapoikkeavia. Kaasun tekemä työ on∫∆W = P dV = P∆V. (3.37)Systeemiin siirtyneeksi lämmöksi saadaan yhtälön (3.24) mukaisesti∆Q = C P ∆T. (3.38)

3.5. KVASISTAATTISIA IDEAALIKAASUPROSESSEJA (˜2.1, 2.11) 25Esimerkki isobaarisesta prosessista on ideaalikaasun laajeneminen lämmitettäessäkitkattomalla männällä varustetussa säiliössä. Laajenemisen aikanamännän ja ympäristön aiheuttama paine pysyy vakiona.3.5.3 Isokoorinen prosessiIsokoorisessa prosessissa systeemin tilavuus pysyy vakiona. Ideaalikaasulleisokoorinen tilanyhtälö onP= vakio. (3.39)TSuljetun kiinteäseinäisen ideaalikaasulla täytetyn säiliön lämmitys on esimerkkiisokoorisesta prosessista. Vaikka kaasu lämpenee, se ei tee tilavuudenmuutostyötä,koska säiliön seinät eivät voi liikkua. Ensimmäisen pääsäännön perusteellasiirtynyt lämpömäärä on yhtä suuri kuin energian muutos ∆U:missä jälkimmäinen muoto seuraa yhtälöstä (3.23).3.5.4 Adiabaattinen prosessiMääritellään adiabaattinen prosessi:∆U = ∆Q = C V ∆T, (3.40)Adiabaattisessa prosessissa systeemin ja ympäristön välillä ei olelämmönvaihtoa eli d¯Q = 0.Ensimmäisestä pääsäännöstä seuraa, että systeemin ympäristöönsä tekemä työadiabaattisessa prosessissa on∆W adiab = −∆U. (3.41)Tästä saadaan lämmölle vaihtoehtoinen tulkinta: ∆Q on energiatasapainonsäilyttämiseksi tarvittava korjaustermi ei-adiabaattisissa muutoksissa. Vaikka d¯Q =0, ei adiabaattinen prosessi ole välttämättä kvasistaattinen, sillä myös systeeminsisällä voi tapahtua työn piiriin kuulumattomia ilmiöitä, jotka poikkeuttavatsen tasapainosta. Asiaa valaisee kuva 3.5.Ideaalikaasun kvasistaattista adiabaattista laajenemista voidaan kuvata kuvan3.4 mäntä-sylinterikonfiguraatiolla, missä sylinteri ja mäntä kuitenkinmuodostavat lämpöeristetyn kokonaisuuden. Tässäkin tapauksessa P ulk < Pmutta paineiden erotus on pieni, jotta männän liike pysyy hitaana, mutta nytlämpöä ei siirry d¯Q = 0, josta seuraa, että lämpötila muuttuu dT ̸= 0. Ensimmäisestäpääsäännöstä saadaand¯Q = 0 = dU+PdV =( ∂U∂T)VdT+( ) ∂UdV+PdV.∂V TTässä(∂U/∂T) V = C V ja (∂U/∂V) T = 0 (koska U = U(T)), joten0 = C V dT+PdV = C V dT+ k B NT dV V ,

26 LUKU 3. TERMODYNAMIIKAN ENSIMMÄINEN PÄÄSÄÄNTÖKaasuaMoottoriAdiabaattinen seinäKuva 3.5: Moottori pyörittää potkuria, joka sekoittaa kaasua. Säiliön seinä eiläpäise lämpöä eli se on adiabaattinen. Sekoitusprosessi on adiabaattinen muttaei kvasistaattinen.missä jälkimmäisessä muodossa on käytetty ideaalikaasun tilanyhtälöä. JakamallaT:llä saadaanC VdTT + k BN dV V = 0,josta integroimalla T 0 → T ja V 0 → VC V ln T T 0+ k B N ln V V 0= 0.Siirtämällä C V ln T 0 ja k B N ln V 0 oikealle puolelle ja yhdistämälle ne vakioksi,ja käyttämällä vasemmalla puolella logaritmien laskusääntöjä saadaan( )ln T C VV k BN= vakio ′′ ,josta seuraaT C VV k BN = vakio’,ja kun muistetaan, että C P − C V = k B N, saadaanTV (C P−C V )/C V= vakio. (3.42)Määritellään adiabaattivakio 2γ = C P /C V = f /2+1f /2> 1, (3.43)jolloin yhtälö (3.42) tulee muotoonTV γ−1 = vakio. (3.44)Tulos on ideaalikaasun adiabaattinen tilanyhtälö. Sijoittamalla ideaalikaasun tilanyhtälöyhtälöön (3.44) saadaan myös muodotPV γ = vakio 2 (= Nk B vakio) (3.45)2 Määritelmä γ = C P /C V pätee ideaalikaasulle, ei yleisesti.

3.5. KVASISTAATTISIA IDEAALIKAASUPROSESSEJA (˜2.1, 2.11) 27PAdiabaattiIsotermiƒVKuva 3.6: Isotermi (dT = 0) ja adiabaatti (d¯Q = 0) (P, V)-tasossa.jaTP (1−γ)/γ = vakio 3(= vakio 1/γ (Nk b ) (γ−1)/γ) . (3.46)Nyt voimme vihdoin laskea ideaalikaasun tekemän työn adiabaattisessalaajenemisessa. Käyttämällä adiabaattisen tilanyhtälön muotoa (3.45) saadaanja työksi tulee∆W =∫ V2(= 11−γV 1PdV =vakioV γ 2∫ V2V 1P = vakioV γ (3.47)vakioV γdV = vakio1−γ( )V 1−γ2− V 1−γ1)V 2 − vakioV γ V 1 = 11−γ (P 2V 2 − P 1 V 1 ). (3.48)1Samaan tulokseen päästään tietenkin myös laskemalla kaavassa (3.41) esiintyväenergian muutos käyttäen ideaalikaasun energian lauseketta U =f /2k B NT ja tilanyhtälöä (3.44), kun huomataan että ideaalikaasulle 1/(1 −γ) ≡ C V /(C V − C P ) = − f /2.Jos kyseessä on reaalikaasu, (∂U/∂V) T ̸= 0, ja on adiabaattisen tilanyhtälönjohtamiseksi integroitava koko adiabaattisuusehto[( ) ] ∂UC V dT+ + P dV = 0. (3.49)∂VAdiabaattisen ja isotermisen ideaalikaasuprosessin käyttäytyminen (P, V)-tasossa nähdään vertaamalla adiabaattisen ja isotermisen tilanyhtälön antamiapainekäyrän kulmakertoimia. Yhtälön (3.45) mukaisesti adiabaattisessa prosessissaP = vakio·V −γ ,T

28 LUKU 3. TERMODYNAMIIKAN ENSIMMÄINEN PÄÄSÄÄNTÖjoten∂P∂V = −vakio·γV−γ−1 = −γV −1 P. (3.50)Toisaalta isotermisessä prosessissaP = vakio·V −1 ,josta saadaan∂P∂V = −vakio·V−2 = −V −1 P. (3.51)Vertaamalla yhtälöitä (3.50) ja (3.51) saadaan( ) ( )∂P∂P= γ . (3.52)∂V adiab ∂V TKoska γ > 1, nähdään yhtälöstä (3.52), että adiabaatit ovat jyrkempiä kuinisotermit (katso kuva 3.6). Tämä tarkoittaa, että kun siirrytään tietystä (P, V)-pisteestä suuremman tilavuuden suuntaan, isotermin alle jää (P, V)-tasossasuurempi pinta-ala kuin adiabaatin alle: kaasun tekemä työ isotermisessämuutoksessa on suurempi kuin adiabaattisessa. Isotermisessä laajenemisessaloppupaine on suurempi kuin adiabaattisessa laajenemisessa. Nämä tuloksetvoi ymmärtää sillä perustella, että toisin kuin adiabaattisessa prosessissa,isotermisessä prosessissa systeemiin virtaa energiaa lämmön muodossa,ja osa tästä energiasta voidaan käyttää työksi. Toisaalta, kun ympäristö tekeekaasuun työtä, eli siirrytään pienemmän tilavuuden suuntaan, tarvitaanadiabaattisessa puristuksessa suurempi työ kuin isotermisessä saman tilavuudenmuutoksen aikaansaamiseksi. Adiabaattisen puristuksen loppupaine onmyös suurempi kuin isotermisen puristuksen. Jälleen on ymmärrettävää, ettäadiabaattisessa prosessissa jossa lämmön virtaus ulos on estetty, puristaminenjohtaa lämpötilan nousuun ja paine kasvaa näin ollen nopeammin kuin vakiolämpötilantapauksessa.Adiabaattiset muutokset ovat keskeisessä asemassa mm. ilmakehän fysiikassa.Troposfäärin konvektiovirtaukset kuljettavat ilmaa ylöspäin ja takaisin.Kohotessaan meren pinnan tasolta ilma laajenee, koska paine pienenee. (vrt.ideaalikaasulaki). Ilma johtaa lämpöä huonosti, joten kohoavan ilmapaketinja ympäristön välillä on vain vähän lämmönvaihtoa, ja laajenemista voidaanpitää adiabaattisena. Tästä seuraa, että nousevan ilmapaketin lämpötila laskee.Laskeva ilmapaketti taas puristuu adiabaattisesti ja sen lämpötila kasvaa.

Luku 4Termodynamiikan toinenpääsääntö4.1 Toinen pääsääntö ja Carnot’n kone (5.2)Höyrykoneen kehittyminen 1700-luvulla johti pohdintoihin termodynaamisistakoneista ja niiden tehokkuudesta. Vähitellen selvisi, että työn muuttaminenlämmöksi on aina mahdollista ja jopa niin, että työ voidaan kokonaisuudessaanmuuttaa lämmöksi. Käytännön sovellusten kannalta mielenkiintoisempaaon kuitenkin tietää, missä määrin lämpöä voidaan muuttaa työksi: kuinkapaljon ja miten vaikkapa hiiltä on poltettava, että höyrykone tekisi työtä mahdollisimmantehokkaasti. Termodynamiikan ensimmäinen pääsääntö kertoo,että energiaa voidaan muuntaa muodosta toiseen, mutta se ei aseta muunnoksellemitään ehtoja. Sen sijaan termodynamiikan toisena pääsääntönä tunnettu empiirinenhavainto rajoittaa mahdollisuutta muuntaa lämpöä työksi.Teoreettisesti termodynaamisten prosessien tehokkuutta tarkasteli ensimmäisenäSadi Carnot (1796–1832). Carnot’n tarkastelut nojaavat reversiibelinprosessin käsitteeseen:Prosessi on reversiibeli eli palautuva, jos on olemassa vastaprosessi,joka palauttaa systeemin takaisin alkutilaan ikään kuin mitäänmuutosta ei olisi tapahtunutkaan. Muutoin prosessi on irreversiibelieli palautumaton. Reversiibelissä prosessissa myös ympäristössätapahtuneet muutokset palautuvat ennalleen.Tämä reversiibelin prosessin määritelmä on mahdollisimman yleinen, eikäse ota mitään kantaa tasapainotiloihin. On kuitenkin vaikea kuvitella sellaistareversiibeliä prosessia, joka ei olisi myös kvasistaattinen, eli se ei kulkisikaantasapainotilojen kautta: siirtyminen epätasapainotilaan aiheuttaisi vääjäämättäirreversiibelin muutoksen. Toisaalta on mahdollista argumentoida, että kvasistaattinenprosessi voi olla irreversiibeli. Esimerkiksi kaasujen hyvin hidastasekoittumista voidaan pitää kvasistaattisena prosessina, mutta se ei millään

30 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖT 2∆Q 2C∆W∆Q 1T 1 (< T 2 )Kuva 4.1: Carnot’n koneen periaatekuva.muotoa ole reversiibeli- käänteistä prosessia eli kaasujen hidasta erottamistatoisistaan ei voida ajatella tapahtuvan. Mutta koska muutos on irreversiibeli,täytyy siinä esiintyä myös vaiheita, jotka eivät ole tasapainotilassa, toisin sanoenmuutos ei olekaan kvasistaattinen! On siis ilmeistä, että jos kvasistaattinenja reversiibeli muutos määritellään kuten edellä, voidaan sanoja reversiibelija kvasistaattinen käyttää toistensa synonyymeinä.Kaasujen sekoittumisen lisäksi tyypillinen esimerkki irreversiibelistä muutoksestaon lämpötilojen tasaantuminen kahden kappaleen välillä. Lisäksikaikki luonnolliset prosessit ovat irreversiibeleitä. Reversiibeli prosessi onkineräänlainen idealisaatio, vaikka luonnollinen prosessi voikin olla lähes reversiibeli.Carnot totesi, että lämpötilaerojen läsnäollessa voidaan lämpöä muuttaatyöksi. Muunnosprosessin tehokkuuden arviointia varten Carnot postuloi kiertoprosessin,Carnot’n koneen (kuva 4.1):Carnot’n kone on lämpövoimakone, joka toimii reversiibelisti kahdenlämpösäiliön välillä.Carnot’n kone• ottaa kuumemmasta lämpösäiliöstä T 2 lämpöenergiaa määrän ∆Q 2 > 0,• tekee työtä määrän ∆W ja• siirtää kylmempään lämpövarastoon T 1 lämpömäärän ∆Q 1 > 0.Tässä sekä ∆Q 1 että ∆Q 2 ovat määritelty positiivisiksi. Lämpövarastot T 1 ja T 2oletetaan niin suuriksi, että koneen toiminta ei vaikuta niiden lämpötiloihin.Carnot päätteli, että kaikkein tehokkain lämpökone toimii kiertoprosessinakahden lämpösäiliön välillä. Lisäksi prosessin tulee olla reversiibeli eli prosessiavoidaan yhtä hyvin ajaa takaperin. Voidaankin määritellä, että mikä tahan-

4.1. TOINEN PÄÄSÄÄNTÖ JA CARNOT’N KONE (5.2) 31sa kahden lämpösäiliön välillä toimiva reversiibeli kiertoprosessi on Carnot’nkone.Koska prosessi on syklinen, palaa systeemi jokaisen työvaiheen jälkeenaina alkutilaan ja sisäisen energian muutos ∆U = 0. Silloin ensimmäisenpääsäännön perusteella∆W = ∆Q 2 − ∆Q 1 . (4.1)Prosessin tehokkuutta kuvaa hyötysuhde η, joka määritellään koneen tekemäntyön ja sen ottaman lämmön suhteena, eliη = ∆W∆Q 2= 1− ∆Q 1∆Q 2, (4.2)missä jälkimmäinen yhtäsuuruus seuraa yhtälöstä (4.1).On selvää, että lämpö siirtyy aina kuumemmasta lämpövarastosta kylmempäänsilloin, kun kone tekee työtä ympäristöönsä. Muutoinhan kone tuottaisioman energiansa, mikä on energian säilymislain eli termodynamiikan ensimmäisenpääsäännön vastaista. Tällaista energian säilymislakia rikkovaa konettasanotaan ensimmäisen lajin ikiliikkujaksi. Mutta voiko Carnot’n kone muuttaakaiken lämmön työksi? Vastaus on ei, sen estää termodynamiikan toinenpääsääntö.Toisesta pääsäännöstä on olemassa useita muotoja. Rudolf Clausius (1822–1888) esitti seuraavan formulaation:Lämpöä ei voida siirtää kylmemmästä lämpövarastosta kuumempaanilman muita muutoksia.Lordi Kelvin eli William Thomson (1824–1907) taas totesi:Kiertoprosessissa ei ole mahdollista ottaa lämpöenergiaa kuumastalämpövarastosta ja muuttaa se työksi, jollei samalla lämpöä siirrykylmempään lämpövarastoon.Clausiuksen ja Kelvinin muotoilut ovat ekvivalentteja. Jos Kelvinin väite eiolisi voimassa, voitaisiin rakentaa lämpövoimakone, joka muuntaa kaikenlämmön työksi. Tämä työ voitaisiin kokonaisuudessaan muuttaa lämmöksija käyttää jonkin kappaleen lämmittämiseen sen alkuperäisestä lämpötilastariippumatta. Jos kappale on kuumempi kuin lämpövarasto, josta lämpöalunperin otettiin, on lopputuloksena lämmön siirtyminen kylmemmästäkappaleesta (lämpövarasto) kuumempaan, mikä on Clausiuksen väitteenvastaista. Jos toisaalta Clausiuksen väite ei olisi voimassa, minkä tahansalämpövoimakoneen hukkalämpö voitaisiin siirtää takaisin korkeammassalämpötilassa olevaan lämpövarastoon. Lämpöä ei tällöin siirtyisi lainkaan kylmempäänlämpövarastoon, mikä on Kelvinin väitteen vastaista.Toisesta pääsäännöstä seuraa, että Carnot’n koneen hukkalämpö ∆Q 1 onaina olemassa. Jos näin ei olisi, Kelvinin toisen pääsäännön muotoilu ei pätisija olisi mahdollista muuttaa kaikki lämpö työksi. Tuloksena olisi toisen lajinikiliikkuja.

32 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖT 2∆Q H2∆Q C2H∆W HC∆Q H1∆Q C1T 1 (< T 2 )Kuva 4.2: Carnot’n kone lämpöpumppuna, jota ajaa hypoteettinen irreversiibelikone H.Kuten todettiin, voidaan Carnot’n prosessi reversiibeliytensä vuoksi myöskääntää vastakkaiseen suuntaan, jolloin koneeseen täytyy tehdä työtä, jottalämpö siirtyisi kylmemmästä kuumempaan lämpövarastoon. Carnot’n konetoimii tällöin lämpöpumppuna. Lämpöpumppua käsitellään tarkemmin kappaleessa4.3.Seuraavaksi todistamme, että Carnot’n kone on kaikista lämpövoimakoneistatehokkain ja että Carnot’n koneen hyötysuhde riippuu ainoastaanlämpövarastojen lämpötiloista. Vertaillaan samojen lämpövarastojen välillätoimivaa Carnot’n konetta C ja hypoteettista irreversiibeliä konetta H (kuva4.2).Oletetaan, että kone H on tehokkaampi kuin Carnot’n kone, η H > η C , eli∆W H∆Q H2> ∆W C∆Q C2. (4.3)Laitetaan nyt Carnot’n kone toimimaan lämpöpumppuna siten, että Carnot’nkone käyttää kaiken koneen H tekemän työn eliSilloin yhtälön (4.3) mukaan∆W C = ∆W H .∆Q C2 > ∆Q H2 .Tästä seuraa, että koneiden C ja H muodostama yhdistetty kone ei tee työtämutta siirtää positiivisen määrän lämpöä∆Q C2 − ∆Q H2 > 0kylmemmästä lämpövarastosta T 1 kuumempaan lämpövarastoon T 2 . Tämä onvastoin Clausiuksen toisen pääsäännön muotoilua, joten kone H ei voi ollaCarnot’n konetta tehokkaampi.

4.1. TOINEN PÄÄSÄÄNTÖ JA CARNOT’N KONE (5.2) 33T 2∆Q R2∆Q C2R∆W RC∆Q R1∆Q C1T 1 (< T 2 )Kuva 4.3: Hypoteettinen reversiibeli kone R lämpöpumppuna, jota ajaa Carnot’nkone C.Todistelumme osoittaa, että η C ≥ η H . Erityisesti, jos kone H on reversiibelikone R, saamme ehdon η C ≥ η R . Mutta silloin kone R voidaan laittaa toimimaanlämpöpumppuna, johon Carnot’n kone tekee työtä (kuva 4.3).Oletetaan, että Carnot’n kone C on tehokkaampi kuin reversiibeli kone R,η C > η R , eli∆W C> ∆W R, (4.4)∆Q C2 ∆Q R2ja kun Carnot’n koneen tekemä työ syötetään reversiibeliin koneeseen,seuraa∆W C = ∆W H ,∆Q C2 < ∆Q R2 .Tästä seuraa, että koneiden C ja R muodostama yhdistetty kone ei tee työtämutta siirtää positiivisen määrän lämpöä∆Q R2 − ∆Q C2 > 0kylmemmästä lämpövarastosta T 1 kuumempaan lämpövarastoon T 2 . Tämä onjälleen vastoin Clausiuksen toisen pääsäännön muotoilu, joten seuraa ristiriitaja on oltava η C ≤ η R .Koska molempien ehtojen täytyy olla voimassa, on väistämättä η C = η R .Siten kone R on myös Carnot’n kone. Voimme siis todeta:Kaikista lämpötilojen T 1 ja T 2 välillä työskentelevistä lämpökoneistaCarnot’n koneella on korkein mahdollinen hyötysuhde.

34 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖT 3∆Q 3∆W 23C∆Q 2T 2∆Q 2∆W 12C∆Q 1T 1Kuva 4.4: Kaksi peräkkäistä Carnot’n konetta.Tätä voidaan myös pitää eräänä termodynamiikan toisen pääsäännön muotoiluna.Koska esittämämme todistelu ei ota kantaa Carnot’n koneen rakenteeseenvaan ainoastaan äärilämpötiloihin T 1 ja T 2 , on myös voimassaη Carnot = f(T 1 , T 2 ),eli Carnot’n koneen hyötysuhde riippuu vain lämpövarastojen lämpötiloista.4.2 Absoluuttinen lämpötila (5.14)Carnot’n kone tarjoaa mahdollisuuden määritellä absoluuttinen lämpötilaasteikko.Koska Carnot’n koneiden hyötysuhde riippuu vain äärilämpötiloista,on kuvan 4.4 kahden peräkkäin kytketyn Carnot’n koneen hyötysuhdeOn myös voimassa1− η Carnot = ∆Q ulos∆Q sis= f(T max , T min ). (4.5)f(T 3 , T 2 ) = ∆Q 2∆Q 3; f(T 2 , T 1 ) = ∆Q 1∆Q 2; f(T 3 , T 1 ) = ∆Q 1∆Q 3,

4.3. CARNOT’N JÄÄKAAPPI JA LÄMPÖPUMPPU (5.11) 35T 2∆Q 2C∆W∆Q 1T 1 (< T 2 )Kuva 4.5: Käänteisen Carnot’n koneen periaatekuva.joista yhdessä tuloksen (4.5) saadaanf(T 3 , T 2 ) f(T 2 , T 1 ) = ∆Q 2∆Q 3∆Q 1∆Q 2= ∆Q 1∆Q 3= f(T 3 , T 1 ) = 1− η Carnot . (4.6)Yhtälöllä (4.6) ei ole yksikäsitteistä ratkaisua. Tapana on määritellä lämpötilatsiten, ettäf(T 2 , T 1 ) = T 1T 2, (4.7)mikä on yhtälön (4.6) yksinkertaisin ratkaisu. Yhtälö (4.7) määrittelee absoluuttisenlämpötila-asteikon mittayksikköä vaille. Carnot’n koneelle on siis voimassaη Carnot = 1− ∆Q ulos∆Q sis= 1− T minT max. (4.8)Yhtälöä (4.7) ehdotti ensimmäisenä Kelvin. Absoluuttisen lämpötilan asteikkonakäytetäänkin kelvinasteikkoa, jossa 1 K = 1°C ja 0°C = 273,15 K.Näin määriteltynä absoluuttinen lämpötila T on ekvivalentti ideaalikaasulämpötilanθ kanssa, kuten kappaleessa 4.4 näemme.4.3 Carnot’n jääkaappi ja lämpöpumppu (5.11)Jo edellä viitattiin mahdollisuuteen käyttää Carnot’n konetta lämpöenergiansiirtämiseen kylmemmästä lämpövarastosta kuumempaan, kunhan vainympäristö tekee tarpeeksi työtä Carnot’n koneeseen. Tällaisen käänteisenCarnot’n prosessin kaavio on esitetty kuvassa 4.5. Jos kylmemmästä lämpövarastostaT 1 otetaan lämpömäärä ∆Q 1 ja siirretään ∆Q 2 kuumempaanlämpövarastoon T 2 , on kiertoprosessissa tehtävän työn määrä∆W = ∆Q 2 − ∆Q 1 .

36 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖCarnot’n koneelle ∆Q 1 /∆Q 2 = T 1 /T 2 , joten∆Q 2∆W = ∆Q 2∆Q 2 − ∆Q 1= T 2T 2 − T 1.Tästä saadaan työksi∆W = T (2− T 1∆Q 2 = 1− T )1∆Q 2 .T 2 T 2Koska T 1 /T 2 < 1, saadaan tulos∆W < ∆Q 2 .Tästä nähdään, että lämpövarastoon T 2 siirtyy enemmän lämpöä kuin työtätehdään.Jääkaappi on käänteinen Carnot’n prosessi, jossa lämpöä siirretään poisympäristöään kylmemmästä systeemistä. Jääkaapin tehokkuutta on tapana mitatatehokertoimen ω avulla. Jääkaapille tehokerroin määritellään kylmemmästälämpövarastosta otetun lämmön ja tehdyn työn suhteena:Erityisesti Carnot’n jääkaapilleω jk = ∆Q 1∆W . (4.9)ω jk,Carnot = T 1T 2 − T 1. (4.10)Tehokerroin voi olla huomattavasti ykköstä suurempi luku.Lämpöpumppu siirtää lämpöä ympäristöä lämpöisempään systeemiin.Lämpöpumpun tehokerroin on kuumempaan lämpövarastoon siirretyn lämpömääränja tehdyn työn suhde:ja Carnot’n lämpöpumpun tehokerroin onω lp = ∆Q 2∆W , (4.11)ω lp,Carnot = T 2T 2 − T 1. (4.12)Lämpöpumppua käytetään mm. talojen lämmitykseen (esimerkiksi maa- taiilmalämpöpumppu).Carnot’n jääkaapin ja lämpöpumpun tehokertoimet on esitetty kuvassa 4.6.Kuvasta nähdään, että molempien prosessien tehokkuus on suurimmillaan,kun lämpötilojen ero pieni. Tästä seuraa mm. että ilmalämpöpumppua ei kannatakäyttää kovilla pakkasilla. Jääkaapin tehokerroin menee nollaan suhteenT 1 /T 2 myötä. Sen vuoksi absoluuttista nollapistettä ei voida saavuttaa Carnot’nkoneella jäähdyttämällä edes periaatteessa.

4.4. IDEAALIKAASUKONEITA (5.2) 3754Tehokerroin321ω lpω jk00 0.2 0.4 0.6 0.8 1.0T 1 /T 2Kuva 4.6: Carnot’n jääkaapin ja lämpöpumpun tehokertoimet lämpösäiliöidenlämpötilojen suhteen T 1 /T 2 funktiona.4.4 Ideaalikaasukoneita (5.2)4.4.1 Carnot’n koneKaikilla kahden lämpövaraston välillä toimivilla reversiibeleillä lämpökoneillaon sama hyötysuhde, ts. ne ovat Carnot’n koneita. Tarkastelemme tässä yksinkertaistaideaalikaasua työaineena käyttävää Carnot’n kiertoprosessia, jokakoostuu kahdesta isotermistä ja kahdesta adiabaatista (kuva 4.7).•Vaihe 1 → 2: isoterminen laajeneminen, T = T k . Ideaalikaasulle(∂U/∂V) T = 0, joten isotermillä ∆U = 0. Ensimmäisen pääsäännön nojalla 1kaasun tekemä työ on∆Q 12 = ∆W 12 =∫ V2V 1PdV = k B NT k ln V 2V 1> 0.•Vaihe 2 → 3: adiabaattinen laajeneminen, T = T k → T m < T k . Adiabaattisuudenvuoksi d¯Q = 0 eli( ) ∂UdU+d¯W = 0 = dT+d¯W = C V dT+d¯W,∂T Vjoten kaasun tekemä työ on∆W 23 = −C V∫ TmT kdT = C V (T k − T m ) > 0.•Vaihe 3 → 4: isoterminen puristus, T = T m . Samoin perustein kuin vaiheessa1 → 2∆Q 34 = ∆W 34 =∫ V4V 3PdV = k B NT m ln V 4V 3< 0.1 Koska käytämme ensimmäistä pääsääntöä, on järkevää siirtyä jälleen alkuperäiseen merkkikonventioon,missä ∆Q:n merkki määräytyy lämpövirran suunnan mukaan.

38 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖP1T kT m243Kuva 4.7: Carnot’n kiertoprosessi (P,V)-tasossa.VHuomaa, että koska V 4 < V 3 , on työkontribuutio negatiivinen. Tässä vaiheessaympäristö tekee kaasuun työtä.•Vaihe 4 → 1: adiabaattinen puristus, T = T m → T k . Tehty työ on∆W 41 = C V (T m − T k ) = −∆W 23 < 0.Syklin aikana tehty kokonaistyö onja hyötysuhde onjosta∆W = ∆W 12 + ∆W 23 + ∆W 34 + ∆W 41 = ∆Q 12 + ∆Q 34= k B NT k ln V 2V 1− k B NT m ln V 3V 4.η = ∆W∆Q 12= 1− k BNT m ln(V 3 /V 4 )k B NT k ln(V 2 /V 1 ) . (4.13)Adiabaattiselle ideaalikaasuprosessille TV γ−1 = vakio, jotenT k V γ−12= T m V γ−13jaT k V γ−11= T m V γ−14,( ) γ−1 ( ) γ−1 V2 V3= ⇔ V 2= V 3.V 1 V 4 V 1 V 4Sijoittamalla tämä tulos yhtälöön (4.13), saadaan hyötysuhteeksiη = 1− T mT k(4.14)

4.4. IDEAALIKAASUKONEITA (5.2) 39eli Carnot’n koneen hyötysuhde. Tulos pätee riippumatta siitä, mitä työainettaCarnot’n kone käyttää. Jotta kone olisi Carnot’n kone, sen on otettava lämpöätietyssä vakiolämpötilassa ja luovuttettava sitä toisessa vakiolämpötilassa.Otto-kiertoprosessi, jota seuraavaksi tarkastellaan, on esimerkki koneesta jossanäin ei ole.Tässä on huolettomasti käytetty merkintää T lämpötilalle, vaikka itse asiassakyseessä on ideaalikaasulämpötila θ (huomaa, että lämpötila-asteikkoonviittaava yleinen kaasuvakio supistuu lopputuloksista pois). Yhtälöt (4.8) ja(4.14) kuitenkin osoittavat, että Carnot’n koneen ottaman ja luovuttamanlämpömäärän suhdetta kuvaavat samanmuotoiset yhtälöt∆Q 1∆Q 2= T 1T 2= θ 1θ 2. (4.15)Asteikkojen ero on vain niiden skaalauksessa. Jos valitaan, että ne yhtenevätveden kolmoispisteessä 273,16 K, vastaavat ideaalikaasu- ja kelvinlämpötilatlukuarvoiltaan toisiaan.4.4.2 Otto-kiertoprosessiOtto-prosessi on polttomoottorin teoreettinen perusta. Polttomoottoria kehittisaksalainen Nikolaus Otto (1832–1891). Otto-prosessi koostuu vuorottaisistaadiabaattisista ja isokoorisista vaiheista (kuva 4.8), työaineena jälleen ideaalikaasu:•Vaihe 1 → 2: adiabaattinen puristus, ∆Q 12 = 0.•Vaihe 2 → 3: isokoorinen paineen kasvu, ∆W 23 = 0. Ensimmäisestäpääsäännöstä∆Q 23 = ∆U =∫ T3T 2C V dT = C V (T 3 − T 2 ).Ideaalikaasun isokoorisen tilanyhtälön (3.39) mukaisesti vaiheen päätepisteissäP 3T 3= P 2T 2. (4.16)Koska P 3 > P 2 , nähdään yhtälöstä (4.16), että T 3 > T 2 . Siten ∆Q 23 > 0.•Vaihe 3 → 4: adiabaattinen laajeneminen, ∆Q 34 = 0.•Vaihe 4 → 1: isokoorinen paineen aleneminen, ∆W 41 = 0, ∆Q 41 =C V (T 1 − T 4 ). Vaiheen päätepisteissäP 4T 4= P 1T 1,ja koska P 4 > P 1 , on T 4 > T 1 ja ∆Q 41 < 0.Systeemin tekemä kokonaistyö kiertoprosessissa on∆W = ∆Q 23 + ∆Q 41 = C V (T 3 − T 2 + T 1 − T 4 )

40 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖP324V 21V 1VKuva 4.8: Otto-kiertoprosessi (P,V)-tasossa.ja hyötysuhdejostaη = ∆W∆Q 23= T 3−T 2 + T 1 − T 4T 3 − T 2= 1− T 4−T 1T 3 − T 2. (4.17)Adiabaattisessa prosessissa (huom V 4 = V 1 ja V 3 = V 2 )Kirjoittamalla yhtälö (4.17) muotoonja käyttämällä tulosta (4.18) saadaanT 4 V γ−11= T 3 V γ−12jaT 1 V γ−11= T 2 V γ−12,T 1T 4= T 2T 3. (4.18)η = 1− T ( )4 1− T1 /T 4T 3 1− T 2 /T 3η = 1− T 4T 3. (4.19)Yhtälö (4.19) on samanmuotoinen kuin Carnot’n prosessille, mutta Ottoprosessinhyötysuhde on kuitenkin pienempi, koska lämmön otto ja luovutusei tapahdu äärilämpötiloissa (vaiheet 2 → 3 ja 4 → 1). T 4 ei myöskään oleprosessin minimilämpötila, koska T 4 > T 1 .On olemassa myös muita prosesseja kuin edellä esitetty isotermisistäja adiabaattisista vaiheista koostuva Carnot’n prosessi, joilla on Carnot’n

4.5. CLAUSIUKSEN EPÄYHTÄLÖ (5.6) 41Systeemid¯W sysTd¯QCd¯W Cd¯Q 0T 0Kuva 4.9: Systeemi, joka on kytketty lämpövarastoon Carnot’n koneen kautta.hyötysuhde. Tällainen on mm. Stirlingin sykli, jossa isotermiset ja isokoorisetvaiheet vuorottelevat; jotta Carnot’n hyötysuhde saavutetaan, on kuitenkinoletettava, että lämpö, joka luovutetaan painetta isokoorisesti pienennettäessä,voidaan kierrättää takaisin täysimääräisesti toisen isokoorisen vaiheenaikana. Käytännön koneissa usein sovelletaan prosesseja, joiden teoreettinenhyötysuhde on huonompi kuin Carnot’n koneen. Syy on luonteeltaantekninen: tällaisissa prosesseissa irreversiibeleistä ilmiöistä aiheutuvat häviötpystytään minimoimaan tehokkaammin.4.5 Clausiuksen epäyhtälö (5.6)Clausius vertaili lukuisia reversiibeleitä ja irreversiibeleitä prosesseja ja totesi,että reversiibelissä prosessissa ∆Q/T on säilyvä suure. Siten esimerkiksi Carnot’nkoneelle ∆Q/T pysyy vakiona (vrt. yhtälö (4.8)) mutta jäähtyvälle teekupilleei: kuppi luovuttaa saman lämpömäärän kuin ympäristö ottaa vastaan,mutta kupin lämpötila on korkeampi kuin ympäristön. Nämä pohdinnat johtivatepäyhtälöön, joka nyt tunnetaan Clausiuksen epäyhtälönä ja entropiankäsitteeseen.Tarkastellaan systeemiä, joka on kytketty lämpövarastoon T 0 reversiibelinCarnot’n koneen välityksellä (kuva 4.9). Systeemi tekee työtä, mutta sen rakenteestaja toteutuksesta meidän ei tarvitse tietää mitään. Systeemi voi olla irreversiibeli.Prosessi etenee infinitesimaalisen pienin askelin siten, että Carnot’nkone ottaa lämpövarastosta T 0 lämpömäärän d¯Q 0 , tekee työtä määrän d¯W C jaluovuttaa lämmön d¯Q systeemille. Tästä aiheutuu systeemin pieni paikallinenlämmitys (lämpötila T), jonka ansiosta systeemi tekee työn d¯W sys .

42 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖSovelletaan nyt termodynamiikan ensimmäistä pääsääntöä Carnot’n koneenja systeemin muodostamaan yhdistettyyn systeemiin, joka kuvassa 4.9 onerotettu katkoviivalla. Lämpövirrat d¯Q ja d¯Q 0 sekä tehdyt työt d¯W sys ja d¯W C onmääritety positiivisiksi, kun ne kulkevat kuvan 4.9 nuolien suuntaan. Yhdistetynsysteemin sisäisen energian muutos on U sisään − U ulos elidU = d¯Q 0 −(d¯W C + d¯W sys ) = d¯Q 0 − d¯W,missä d¯W on yhdistetyn systeemin tekemä työ. Carnot’n koneelle päteed¯Q 0T 0= d¯Q T⇔ d¯Q 0 = T 0d¯QT , (4.20)jolloind¯W = d¯Q 0 − dU = T 0d¯QT − dU.Kokonaistyö saadaan, kun integroidaan edellinen yhtälö koko syklin ympäri:∆W = T 0∮ d¯QT − ∮dU.Mutta kiertoprosessissajoten∮dU = 0,∆W = T 0∮ d¯QT .Yhdistetyn systeemin tekemä työ ei voi olla positiivinen, koska muuten kiertoprosessivaihtaisi lämpöä yhden lämpövaraston (T 0 ) kanssa ja tekisi vastaavanmäärän työtä, mikä on vastoin termodynamiikan toista pääsääntöä (Kelvin).Siispä∮ d¯Q≤ 0. (4.21)TTämä on Clausiuksen epäyhtälö.Jos kuvan 4.9 tarkemmin määrittelemätön systeemi olisi reversiibeli,voisimme ajaa prosessia takaperin, siten että Carnot’n kone toimiilämpöpumppuna (kuva 4.10). Seuraavassa lämpövirrat d¯Q ja d¯Q 0 sekä tehdyttyöt d¯W sys ja d¯W C on määritety positiivisiksi, kun ne kulkevat kuvan 4.10nuolien suuntaan. Tällöin yhdistetyn systeemin sisäisen energian muutos olisidU = d¯W C + d¯W sys − d¯Q 0 = d¯W− d¯Q 0 ,missä d¯W on yhdistettyyn systeemiin tehty työ. Käyttämällä Carnot’n koneelleyhtälöä (4.20) saataisiind¯W = dU+T 0d¯QT .

4.6. ENTROPIA (5.3) 43Systeemid¯W sysTd¯QCd¯W Cd¯Q 0T 0Kuva 4.10: Systeemi, joka on kytketty lämpövarastoon lämpöpumppuna toimivankäänteisen Carnot’n koneen kautta.Kokonaistyö saataisiin jälleen kun integroitaisiin edellinen yhtälö koko syklinympäri:∮ ∮ d¯Q d¯Q∆W = dU+T 0 0∮T = T T ,koska kiertoprosessissa∮dU = 0.Yhdistetty systeemi ei voi tehdä työtä ympäristöön rikkomatta toistapääsääntöä (eli ympäristön on tehtävä työtä yhdistettyyn systeemiin, nytkäytössä olevalla merkkisäänöillä siis on oltava ∆W > 0) , joten saadaan tulos∮ d¯Q≥ 0. (4.22)TReversiibelille prosessille täytyy siis molempien tulosten (4.21) ja (4.22) ollavoimassa, jolloin voidaan päätellä, että yhtälön (4.21) yhtäsuuruus on voimassavain ja ainoastaan reversiibelissä tapauksessa.4.6 Entropia (5.3)Kuvassa 4.11 on esitetty eräs kiertoprosessi (P, V)-tasossa. Valitaan prosessinreitiltä kaksi mielivaltaista tilaa 1 ja 2, ja merkitään polkua 1 → 2 kirjaimellaa ja polkua 2 → 1 kirjaimella b. Oletetaan ensin, että prosessi on reversiibeli.

44 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖP2ab1Kuva 4.11: Eräs kiertoprosessi (P, V)-tasossa.VClausiuksen epäyhtälön perusteellajoten∮ d¯Qrev=T∫ 2 d¯Q rev1aT∫ 2 d¯Q rev1aT∫ 1 d¯Q rev= − =2 Tb∫ 1 d¯Q+rev= 0,2 Tb∫ 21bd¯Q revT .Funktio d¯Q rev /T voidaan siis integroida mitä reittiä tahansa pisteestä 1 pisteeseen2: ∫ 2 d¯Q rev= S(P 2 , V 2 )−S(PT1 , V 1 ) ≡ ∆S. (4.23)1Koska integraalin arvo riippuu vain päätepisteistä, on yhtälössä (4.23)määritelty funktio S(P, V) tilamuuttuja. Siitä käytetään Clausiuksen keksimäänimitystä entropia.Oletetaan seuraavaksi, että muutos tilasta 1 tilaan 2 on irreversiibeli, muttatakaisin tilaan 1 palataan reversiibeliä reittiä pitkin. Clausiuksen epäyhtälönperusteella∫ 21d¯Q irrT + ∫ 12d¯Q revT=∫ 21d¯Q irr ∫ 2T − d¯Q rev1 T} {{ }∆S< 0eli∫ 2 d¯Q irr1T< ∆S. (4.24)Irreversiibelissä tapauksessa lämmönvaihtotermi ∫ d¯Q irr /T ei sisällä kaikkiaentropian muutokseen vaikuttavia tekijöitä vaan osa entropian muutoksestatulee systeemin sisäisten spontaanien prosessien aiheuttamasta entropian tuotosta.

4.6. ENTROPIA (5.3) 45Adiabaattisessa prosessissa lämpöä ei siirry d¯Q adiab = 0, joten entropia∆S ≥ 0. Toisin sanoen:Adiabaattisessa prosessissa entropian muutos ∆S = 0, jos prosession reversiibeli, muutoin ∆S > 0.Jos systeemi ei ole adiabaattisesti suljettu, voi systeemin entropia pienentyä∆S < 0, mutta systeemille ja ympäristölle yhteensä ∆S tot ≥ 0. Clausiuksenmuotoilemana tämä vaatimus voidaan esittää seuraavasti:Maailmankaikkeuden entropia pyrkii maksimoitumaan.Tämä toisen pääsäännön formulaatio liittää entropian syvällisellä tavalla ajansuuntaan. Koska kaikki luonnolliset prosessit ovat irreversiibeleitä, voidaanpelkästään prosessia havainnoimalla erottaa aiempi hetki t 1 ja myöhäisempihetki t 2 toisistaan sillä perusteella, että hetkellä t 2 maailmankaikkeudenentropia on suurempi kuin hetkellä t 1 . Jatkossa tasapainotiloja etsittäessäkäytännöllinen toisen pääsäännön muotoilu onSuljetussa systeemissä kaikissa spontaaneissa prosesseissa entropiakasvaa.Entropian (ja lämpötilan) käsitteeseen päädytään myös matemaattisesti elegantillatavalla ottamalla lähtökohdaksi kreikkalaisen matemaatikon ConstantinCarathéodoryn (1873–1950) vuonna 1909 esittämä aksiooma: mielivaltaisenlähellä jokaista makroskooppisen tila-avaruuden pistettä on tasapainotiloja, joitaei voida saavuttaa adiabaattisesti.Tässä menetelmässä termodynamiikan keskeisimmätkäsitteet voidaan esittää termodynaamisiin tiloihin liittyen tarvitsemattapuuttua lämpökoneisiin ja niiden rakenteeseen. Koneisiin perustuvalähestymistapa ei kuitenkaan ole vähemmän yleinen.4.6.1 Entropia ja ensimmäinen pääsääntöClausiuksen epäyhtälön perusteella reversiibelissä prosessissa on voimassadS = d¯QrevT . (4.25)Koska dS on eksakti differentiaali, voidaan todeta, että on T −1 epäeksaktindifferentiaalin d¯Q integroiva tekijä (totea tämä eksplisiittisesti ideaalikaasuntapauksessa). Vastaavasti tilavuudenmuutostyön differentiaalin d¯W tekee eksaktiksitekijä P −1 eli d¯W rev = PdV. Voimme siis kirjoittaa ensimmäisenpääsäännön differentiaaliseen muotoondU = TdS− PdV. (4.26)Nyt voisi kuvitella, että sisäisen energian muutos olisi laskettavissa integroimallayhtälöstä (4.26) vain reversiibelissä tapauksessa:∫ ∫∆U = ∆Q−∆W = TdS− PdV. (4.27)

46 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ2 J1 J0 JKuva 4.12: Kaavakuva energiatasoista.Mutta koska U on tilamuuttuja ja dU on eksakti differentiaali, saadaan ∆Uyhtälöstä (4.27) aina, jos yhtälön oikean puolen integroinnit suoritetaan reversiibeliäreittiä pitkin. Tästä on suurta hyötyä tarkasteltaessa irreversiibeleitämuutoksia.Irreversiibeleistä muutoksista aiheutuu entropian tuottoa, jonka vuoksi∫∆Q irr < TdS.Jotta yhtälö (4.27) olisi voimassa, täytyy olla∫∆W irr < PdV. (4.28)Irreversiibeleissä muutoksissa systeemi tekee siis vähemmän työtä kuin reversiibeleissämuutoksissa.4.6.2 Mitä entropia oikein kuvaa?Entropia S kuvaa makrotasolta katsoen piilossa olevia erilaisia mahdollisia tiloja,joissa systeemi voi olla. Ajatellaan, että voisimme mitata vain systeeminkokonaisenergiaa U, mutta tiedämme että meillä on 5 hiukkasta ja 3 mahdollistaenergiatasoa joilla hiukkaset voivat olla (tasojen energiat 0 J, 1 J ja 2 J, katsokuvaa 4.12):• Jos makrotila on U = 10 J, kaikkien hiukkasten täytyy olla energiatasolla2 J (10 J = 5×2J), joten mahdollisia tiloja on vain yksi.• Jos makrotila on U = 5 J, mahdollisuuksia on useita:2×2 J + 1×1 J + 2×0 J1×2 J + 3×1 J + 1×0 J5×1 J• Kokeile itse tapauksia U = 9,8,7,6,4,3,2,1 J .Tilastollisessa mekaniikassa entropia on määritelty= 3 mahdollisuuttaS = k ln W, (4.29)

4.7. SISÄINEN ENERGIA JA MAXWELLIN RELAATIOT (6.2) 47missä W on makrotasolta piilossa olevien mikroskooppisten mahdollisuuksienlukumäärä ja k on Boltzmannin vakio 1.38·10 −23 J/K. Entropian yksikkö on samakuin Boltzmannin vakion yksikkö [S] = J/K. Kuvan 4.12 systeemin entropiattarkastelluissa tapauksissaU = 10 J → S = k· ln1 = 0U = 5 J → S = k· ln3>0.Miten monella tavalla voidaan N kaasuhiukkasta järjestää tilavuuteen Vniin että niiden energia on U? Kaikkien hiukkasten paikat ja nopeudet voivatolla mielivaltaisia, onko mahdollisuuksia siis äärettömän monta? Vastaus onei, koska kvanttimekaniikassa opimme että paikka ja tilavuuskin ovat kvantittuneita,ne voidaan määritellä vain Heisenbergin epätarkkuusperiaatteen antamallatarkkuudella. Niinpä kaasun entropiakaan ei ole ääretön.HUOM 1: Lämpötila T on verrannollinen hiukkasten yhteenlaskettuun kineettiseenenergiaan.Energia U on yhteenlaskettu vuorovaikutusten potentiaalienergia ja kineettinenenergia.Kineettinen energia voi muuttua potentiaalienergiaksi ja päinvastoin, muttasuljetussa systeemissä kokonaisenergiaa säilyy.HUOM 2: Jako makroskooppiseen ja mikroskooppiseen riippuu mittalaitteistatai mallin/ymmärryksen tasosta: kuinka pieniä yksityiskohtia voimmetai haluamme tarkastella.4.7 Sisäinen energia ja Maxwellin relaatiot (6.2)Sisäisen energian differentiaalimuoto reversiibelissä muutoksessa saadaansuoraan termodynamiikan ensimmäisestä pääsäännöstä:dU = TdS− PdV+ ∑ µdN i . (4.30)iKoska dU on eksakti differentiaali, voidaan kirjoittaadU =( ) ∂UdS+∂S V,N i( ) ( )∂U∂UdV+dN∂V S,N i∂N i . (4.31)i S,V,N j̸=iDifferentiaaleista (4.30) ja (4.31) voimme tehdä identifikaatiot( ) ∂U= T,∂S V,N i( ) ∂U= −P,∂V S,N i( ∂U∂N i)Toisaalta osittaisderivoinnit kommutoivat, esimerkiksi( ) ∂T= ∂∂V S,N i∂V( ( ) )∂U= ∂∂S V,N i∂SS,N iS,V,N j̸=i= µ i . (4.32)( ( ) )∂U= −∂V S,N i V,N i( ) ∂P.∂S V,N i

48 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖdU = T d S − P d V + µ d N ⇒ ∂T∂V= − ∂P∂SKuva 4.13: Kaavio Maxwellin relaatioiden muodostamiseksi.Soveltamalla samaa symmetriaa toisiinkin muuttujiin, saadaan sisäiseen energiaanliittyvät Maxwellin relaatiot( ) ∂T∂V( ) ∂T∂N iS,N iS,V,N j̸=i=( ) ∂P= − , (4.33)∂S V,N( ) i∂µ, (4.34)∂S V,N i( ∂P∂N i)S,V,N j̸=i= −( ) ∂µ(4.35)∂V S,N iMaxwellin relaatioita ei kannata opetella ulkoa, vaan ne voidaan johtaahelposti kuten edellä. Toisaalta ne voidaan myös lukea suoraan sisäisenenergian (tai muun myöhemmin esiteltävän termodynaamisen potentiaalin)differentiaalimuodosta. Esimerkiksi relaatio (4.33) voidaan muodostaa kuvan4.13 mukaisesti valitsemalla muuttujat “ristikkäin” konjugoiduista pareista.Samanlainen kaavio voidaan kirjoittaa myös muille intensiivisen ja ekstensiivisenmuuttujan muodostamille pareille.4.7.1 Fundamentaalinen yhtälö (˜6.4)Kaikki termodynaamiset energiafunktiot ovat luonteeltaan ekstensiivisiä. Koskasisäisen energian luonnolliset muuttujat S, V ja N (katso luku 5.3.1) ovatmyös ekstensiivisiä, voidaan kirjoittaa skaalausehtoU(λS, λV, λN i ) = λU(S, V, N i ). (4.36)Matemaattisesti ilmaistuna tämä tarkoittaa, että sisäinen energia on ensimmäisenkertaluvun homogeeninen funktio. Derivoidaan yhtälö (4.36) λ:nsuhteen:( )d∂Udλ (λU) = ∂λSV,N i( )d ∂Udλ (λS)+ ∂λV S,N i( )d∂Udλ (λV)+ ∑∂λNi i S,V,N j̸=iddλ (λN i).

4.7. SISÄINEN ENERGIA JA MAXWELLIN RELAATIOT (6.2) 49Asetetaan λ = 1, jolloin( ) ∂UU = S + V∂S V,N i( ) ∂U∂V( ) ∂U+ ∑ N i . (4.37)S,N i∂Nii S,V,N j̸=iTämä on Eulerin teoreema ensimmäisen kertaluvun homogeenisille funktioille.Yhdistämällä yhtälö (4.37) ja tulokset (4.32) saadaan fundamentaalinen yhtälö:U = TS− PV+ ∑ µ i N i . (4.38)iFundamentaalista yhtälöä ei voida johtaa suoraan sisäisen energian differentiaalimuodostadU = TdS− PdV+ ∑ i µ i dN i , vaan on vaadittava, että homogeenisuusehto(4.36) on voimassa.4.7.2 Gibbsin ja Duhemin yhtälöDifferentioimalla fundamentaalinen yhtälö saadaandU = TdS+SdT−PdV− VdP+∑iToisaalta sisäisen energian differentiaali ondU = TdS− PdV+ ∑ µ i dN i .iVähentämällä nämä yhtälöt toisistaan saadaaneli yksikomponenttisysteemilleSdT− VdP+∑ Ndµ i = 0iµ i dN i + ∑ N i dµ i .idµ = − S N dT+ V dP. (4.39)NYhtälö (4.39) tai (4.7.2) on Gibbsin ja Duhemin yhtälö. Siitä nähdään, että kemiallisenpotentiaalin luonnolliset muuttujat ovat T ja P (katso luku 5.3.1).Kaksiulotteiselle systeemille, jolla on pinta-ala, mutta ei tilavuutta, kutenfaasien välinen rajapinta fundamentaalinen yhtälö saa muodonja sen kokonaisdifferentiaali onU = TS+∑ µ i N i + AσdU = TdS+SdT+∑ dµ i N i + ∑ µ i dN i + dAσ+ Adσ.Kun tätä verrataan termodynamiikan ensimäiseen pääsääntöönsaadaan Gibbsin adsorptioyhtälödU = TdS+ ∑ µ i dN i + σdASdT+ Adσ+∑N i dµ i = 0. (4.40)Vakiolämpötilassa tästä tulee Gibbsin adsorptioisotermi∑ N i dµ i + Adσ = 0. (4.41)

50 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ4.7.3 Mikä on kemiallinen potentiaali ja miksi se riippuu paineestaja lämpötilasta?Tarkastellaan systeemiä jonka hiukkasmääräkin voi muuttua, ja hiukkasia onmontaa lajia i. Tällöin ensimmäinen pääsääntö reversiibelille muutokselle ondU = TdS− PdV− ∑ µ i dN i (4.42)iKemiallisen potentiaalin määritelmä komponentille i on siis( ) ∂Uµ i =∂N iS,V,N j̸=i.Molekyylityypin i kemiallinen potentiaali µ i on siis systeemin energian muutoskun entropia, kaikkien muiden tyyppisten molekyylien määrät ja tilavuuspidetään vakiona, ja lisätään yksi molekyyli i. Tämä on molekyylienkineettisen ja vuorovaikutusenergian summa kyseisessä systeemissä, ja seriippuu lämpötilasta (kuinka paljon kineettistä energiaa molekyylillä keskimäärinon) ja paineesta tai tiheydestä (kuinka lähellä toisiaan molekyylitovat). Vuorovaikutusenergia riippuu myös molekyyliseoksen koostumuksesta,eli siitä, millaisten molekyylien kanssa molekyyli i vuorovaikuttaa. On vaikeakuvitella käytännössä koejärjestelyä, joka pitää entropian vakiona, siksikäytännöllisemmät kemiallisen potentiaalin määritelmät nojaavat vapaidenenergioiden käsitteisiin (luku 5) energian sijaan. Yleisimmin käytettymääritelmä perustuu Gibbsin vapaaseen energiaan k( ) ∂Gµ i =. (4.43)∂N i T,P,N j̸=iKun myöhemmin määrittelemme Gibbsin vapaan energian on tämä määritelmäkäyttökelpoinen: pidetään systeemin paine ja lämpötila vakioina, ja työnnetäänsysteemin yksi molekyyli i lisää. Systeemin Gibbsin vapaan energian muutoson tällöin kemiallinen potentiaali. Helmholtzin vapaan energian F avulla kemiallinenpotentiaali voidaan selvittää pitämällä tilavuus ja lämpötila vakioina( ) ∂Fµ i =∂N iT,V,N j̸=i.4.8 Esimerkkejä entropian muutoksen laskemisesta(5.4)4.8.1 Ideaalikaasun isoterminen reversiibeli laajeneminenKoska kyseessä on reversiibeli prosessi (sekä systeemin että ympäristön osalta),lasketaan systeemin (kaasu) entropian muutos yhtälöstä (4.25):∆S sys =∫ 21d¯Q revT .

4.8. ESIMERKKEJÄ ENTROPIAN MUUTOKSEN LASKEMISESTA (5.4) 51Ideaalikaasulle U = U(T), joten isotermisessä prosessissa dU = 0 ja d¯Q rev =d¯W = PdV. Systeemin laajetessa tilavuudesta V 1 tilavuuteen V 2 on sen entropianmuutos siis∆S sys =∫ 21PdVT∫ = V2k dVBNV 1V = k BN ln V 2, (4.44)V 1missä toinen yhtäsuuruus seuraa ideaalikaasun tilanyhtälöstä.Mikä on ympäristön entropian muutos? Reversiibelissä prosessissa maailmankaikkeudenentropia ei muutu eli ∆S tot = ∆S sys + ∆S ymp = 0, joten∆S ymp = −∆S sys .4.8.2 Ideaalikaasun irreversiibeli ja adiabaattinen vapaa laajeneminenKoska S on tilamuuttuja, on entropian muutos ∫ Cd¯Q/T laskettuna mitä tahansareversiibeliä reittiä C pitkin. Koska laajeneminen on adiabaattista, on∆Q = 0. Toisaalta vapaassa laajenemisessa kaasu ei tee työtä, joten ∆W = 0.Silloin ensimmäisen pääsäännön perusteella sisäisen energian muutos ∆U = 0.Tästä seuraa, että muutoksen on välttämättä oltava isoterminen, koska ideaalikaasunsisäinen energia riippuu vain lämpötilasta. Siten sopiva reversiibelireitti on isotermi, ja edellisen kohdan mukaisesti muutoksessa V 1 → V 2∆S sys = k B N ln V 2V 1. (4.45)Ympäristön entropian muutos sen sijaan on ∆S ymp = 0, koska adiabaattisuudenvuoksi systeemin ja ympäristön välillä ∆Q = 0. Systeemin jaympäristön entropian muutos on yhteensä∆S tot = ∆S sys + ∆S ymp = ∆S sys + 0 = k B N ln V 2V 1> 0.Kokonaisentropia kasvaa systeemin sisäisen irreversiibelin prosessin seurauksena.4.8.3 Kappaleen lämmitys isokoorisesti tai isobaarisestiLämpökapasiteetti (isokoorinen tai isobaarinen) on määritelmän mukaand¯Q = CdT. Lämmitettäessä kappaletta lämpötilasta T 1 lämpötilaan T 2 entropianmuutos on∆S sys =∫ T2T 1d¯QT= ∫ T2T 1CT dT = C ln T 2T 1, (4.46)jos oletetaan, että lämpökapasiteetti ei riipu lämpötilasta. Ympäristöstä siirtyykappaleeseen lämpöä määrä∆Q =∫ T2T 1CdT = C(T 2 − T 1 )

52 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖja ympäristön (lämpötila T 2 ) entropian muutos on∆S ymp = − ∆QT 2= −C T 2−T 1T 2< 0. (4.47)Miinus-merkki johtuu siitä, että ympäristön kannalta lämpö siirtyy valitunmerkkikonvention puitteissa negatiiviseen suuntaan. Kokonaisentropianmuutos on∆S tot = ∆S sys + ∆S ympMuutos on positiivinen, kun T 2 > T 1 .= C ln T 2− C T 2− T 1T 1 T(2= C ln T 2− 1+ T )1. (4.48)T 1 T 2Esimerkki 4.1Vettä (massa m = 1 kg) lämmitetään isobaarisesti 20 °C→ 80 °C.Veden entropian muutos on∆S sys = C P ln T 2T 1= mc P ln T 2T 1,missä c P on isobaarinen ominaislämpökapasiteetti. Vedelle c P =4, 2 J/gK. Sijoittamalla lukuarvot∆S sys = 1000 g· 4, 2 J/gK· ln 353 K = 782 J/K.293 KYmpäristön entropian muutos on∆S ymp = −mc PT 2 − T 1T 2Entropian kokonaismuutos on= −1000 g·4, 2 J/gK· 60 K = −714 J/K.353 K∆S tot = 782 J/K−714 J/K = 68 J/K > 0.4.8.4 SekoitusentropiaTarkastellaan kahta kaasua, 1 ja 2, kuvan 4.14 mukaisessa säiliössä. Kun kaasujaerottava väliseinä poistetaan, kaasut sekoittuvat. Oletetaan, että kaasut ovatideaalikaasuja ja että alku- ja lopputilojen paineet ovat samat. Kaasujen voidaansilloin kuvitella sekoittuvan isotermisesti ja isobaarisesti. Ideaalikaasujenseokselle päteeP = k BNTV= ∑ik B N i TV= ∑ P i , (4.49)i

4.8. ESIMERKKEJÄ ENTROPIAN MUUTOKSEN LASKEMISESTA (5.4) 531 2Kuva 4.14: Kaasut sekoittuvat, kun väliseinä poistetaan.missä N i on ainekomponentin i hiukkasmäärä ja P i sen osapaine. Tulos (4.49)on Daltonin laki ja se on nimetty englantilaisen kemistin John Daltonin (1766–1844) mukaan. Daltonin laki kertoo, että ideaalikaasuseoksen paine voidaanilmaista kaasun ainekomponenttien osapaineiden summana.Keskeinen käsite seoksia tutkittaessa on mooliosuus. Ainekomponentin imooliosuus määritelläänMooliosuuksille pätee ehtox i = N i∑ i N i= N iN . (4.50)∑ x i = 1. (4.51)iMooliosuus on aina välillä 0 ≤ x i ≤ 1. Yhtälöstä (4.49) saadaan, että erityisestiideaalikaasuseoksen mooliosuuksille päteex i = P iP . (4.52)Huomaa, että yhtälö (4.50) pätee yleisesti kaikille kaasuille, nesteille ja kiinteilleaineille mutta yhtälö (4.52) vain ja ainoastaan ideaalikaasulle.Sekoittumisen voidaan ajatella tapahtuvan siten, että koko tilavuuteenV laajenee ensin kaasu 1 ja sitten kaasu 2. Tämä oletus on mahdollistatehdä, koska ideaalikaasurajalla molekyylien väliset vuorovaikutukset ovathäviävän pieniä. Edellisen luvun perusteella molempien kaasujen entropiakasvaa määrällä k B N i ln(V/V i ), missä V i on kaasun i alkutilavuus. Siten sekoitusentropiaon∆S mix = k B N 1 ln V V 1+ k B N 2 ln V V 2.Koska sekoittuminen tapahtuu vakiopaineessa ja -lämpötilassa, on P 1 = P 2 =P ja T 1 = T 2 = T, jolloin ideaalikaasulaistaN 1V 1= N 2V 2= N V⇒ V iV = N iN = x i.

54 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖNyt sekoitusentropia tulee muotoon∆S mix = k B N 1 ln Vx 1 V + k BN 2 lnVx 2 V= k B N 1 ln 1 x 1+ k B N 2 ln 1 x 2,ja kun vielä käytetään mooliosuuden määritelmää (4.50), saadaan∆S mix = −k B N(x 1 ln x 1 + x 2 ln x 2 ). (4.53)Koska 0 ≤ x i ≤ 1, on ∆S mix ≥ 0. Jos on vain yksi kaasu ja väliseinää eiole, x 2 = 0, x 1 = 1 ja ∆S mix = 0, kuten pitääkin. Jos väliseinä on asetettu niin,että kumpaakin kaasua yhtä monta molekyyliä (moolia), on x 1 = x 2 = 1/2 ja∆S mix = k B N ln 2. Entä, jos kaasut 1 ja 2 ovat samaa kaasua? Silloinhan entropianei pitäisi kasvaa, koska mitään sekoittumista de facto ei tapahdu. Tämä onGibbsin paradoksi. Paradoksi ratkeaa tilastollisessa mekaniikassa. Kvanttimekaniikanperiaatteiden mukaisesti identtiset ja epäidenttiset hiukkaset pitää laskeaeri tavalla, ja tämä ero näkyy myös klassisella rajalla.4.9 Entropian differentiaali ja eräitä sovelluksia(5.12, 3.1, 3.5)Tässä kappaleessa esitämme kuinka entropian kokonaisdifferentiaalia voidaankäyttää johdettaessa eräitä hyödyllisiä tuloksia.4.9.1 Helmholtzin yhtälöOletetaan reversiibeli muutos PTV-systeemissä. Jos riippumattomiksi muuttujiksivalitaan T ja V, saadaan ensimmäisestä pääsäännöstä( ) [( ) ]∂U∂Ud¯Q = dU+PdV = dT+ + P dV.∂T∂VTästä ja yhtälöstä (4.25) entropian differentiaaliksi saadaandS = d¯Q T= 1 ( ) ∂UdT+ 1 [( ) ] ∂U+ P dV. (4.54)T ∂T T ∂VResiprookkisuusehdon nojalla täytyy olla voimassa( )∂ 1 ∂U∂V T ∂T⏐ = ∂ [ ( )]1 ∂UV∂T T ∂V⏐ + PTSuorittamalla derivoinnit1 ∂ 2 UT ∂V∂T = − 1 ( )∂UT 2 ∂V⏐ + P + 1 ∂ 2 UTT ∂V∂T + 1 ∂P⏐T ∂TTVVTTV.⏐V

4.9. ENTROPIAN DIFFERENTIAALI JA ERÄITÄ SOVELLUKSIA (5.12, 3.1,3.5) 55saadaan( ) ∂U= T∂V T,N( ) [ ( )]∂P∂ P− P = T 2 . (4.55)∂T V,N∂T T V,NYhtälö (4.55) on Helmholtzin yhtälö, ja se lausuu sisäisen energian riippuvuudentilavuudesta isotermisissä muutoksissa paineen lämpötilariippuvuudenavulla, joka voidaan määrittää, jos tilanyhtälö tunnetaan. Helmholtzin yhtälötunnetaan myös nimillä ensimmäinen energiayhtälö ja termodynaaminen tilanyhtälö.Ideaalikaasulle (∂U/∂V) T,N = 0, kuten helposti yhtälöstä (4.55) todetaan(vrt. yhtälö (1.9)).4.9.2 Ideaalikaasun entropiaIsokoorisen lämpökapasiteetin C V = (∂U/∂T) V avulla entropian differentiaali(4.54) saadaan muotoondS = 1 T C VdT+ 1 [( ) ] ∂U+ P dV. (4.56)T ∂V TIdeaalikaasun tapauksessa U ei riipu tilavuudesta ja P = k B NT/V, jotenIntegroimalla saadaandS = 1 T C VdT+ 1 Tk B NTVdV = 1 T C VdT+ k BNVdV.S = S 0 + C V ln T T 0+ k B N ln V V 0.Tässä S 0 , V 0 ja T 0 viittaavat johonkin referenssitilaan. Ekstensiivisinä suureinaS 0 ja V 0 voidaan antaa vastaavien tiheyssuureiden avulla muodossa S 0 = s 0 Nja V 0 = v 0 N. Kun vielä lämpökapasiteetti lausutaan yhtälön (3.29) mukaisestimuodossa C V = k B N f /2 (ideaalikaasulle U = k B TN f /2), saadaan ideaalikaasunentropiaksi[ ( ) ]Tf /2VS = s 0 N+k B N ln. (4.57)T 0 v 0 NSuureet s 0 , v 0 ja T 0 ovat mikroskooppisia ainevakioita, joiden laskemiseksi tarvitaantilastollisen mekaniikan menetelmiä.4.9.3 LämpökapasiteettiyhtälötTermodynaamiset vasteet eli responssit kertovat kuinka jonkin systeemiä kuvaavantilamuuttujan A muutos vaikuttaa systeemin ominaisuuteen X, kunmuut riippumattomat tilamuuttujat B, C, . . . pysyvät vakioina. Termodynaamisetvasteet ovat usein mitattavia suureita.Olemme jo tutustuneet eräisiin termodynaamisiin vasteisiin, lämpökapasiteetteihinkappaleessa 3.4. Lämpökapasiteetit määriteltiin lausekkeiksi

56 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖlim ∆T→0 (∆Q/∆T) ehto , missä “ehto” tarkoittaa yleensä vakiotilavuutta tai vakiopainetta.Koska lämpökapasiteetit ovat tasapainosysteemien ominaisuuksia,ne on määriteltävä systeemin infinitesimaalisten reversiibelien muutostenkautta, mikä esimerkiksi yhtälöissä (3.25) ja (3.26) on oletettava. Reversiibelinprosessin tapausessa lämpövuot voidaan lausua entropian muutosten avulla.Kirjoittamalla entropian kokonaisdifferentiaali lämpötilan ja tilavuudendifferentiaalien avulla( ) ( )∂S ∂SdS = dT+ dV∂T V ∂V Tja vertaamalla tätä yhtälöön (4.56)dS = 1 T C VdT+ 1 T[( ) ] ∂U+ P dV,∂V Tsaadaan C V lausuttua entropian lämpötilariippuvuuden avulla:C V = T( ) ∂S. (4.58)∂T VVastaavastid¯Q = TdS ⇒ d¯QdT⏐ = TP( ) ∂S∂T P(4.59)joten isobaarinen lämpökapasiteetti onC P = T( ) ∂S. (4.60)∂T PKappaleessa 3.4 saimme yleiset lausekkeet isobaarisen isokoorisen lämpökapasiteetinerotukselle (yhtälö (3.27)):C P − C V =[( ) ]( ∂U ∂V+ P∂V T ∂TTulos on kuitenkin hieman hankala, koska siinä esiintyy sisäisen energianriippuvuus tilavuudesta (vrt. kuitenkin yhtälö (4.55)). Seuraavassa johdammekäytännölliset yhtälöt lämpökapasiteettien C V ja C P erotukselle ja suhteelle,jotka tunnetaan lämpökapasiteettiyhtälöinä. Samalla tutustumme muutamiintermodynaamisiin vasteisiin.Valitaan riippumattomiksi muuttujiksi paine ja lämpötila. Silloin( ) ( )∂S ∂S(V(P, T), T)= =∂T P ∂T P).P( ) ( )∂S ∂S+∂T V ∂V T( ) ∂V. (4.61)∂T P

4.9. ENTROPIAN DIFFERENTIAALI JA ERÄITÄ SOVELLUKSIA (5.12, 3.1,3.5) 57Helmholtzin yhtälöstä ja differentiaalista (4.56) saadaandS = 1 T C VdT+ 1 [( ) ] ∂U+ P dV (4.62)T ∂V T= 1 T C VdT+ 1 [ ( ) ]∂PT − P+ P dV (4.63)T ∂T V= 1 ( ) ∂PT C VdT+ dV (4.64)∂T V(katso myös yhtälö (5.5)), josta seuraa( ) ∂S=∂VT( ) ∂P. (4.65)∂T VKun yhtälö (4.61) kerrotaan lämpötilalla ja käytetään tulosta (4.65), saadaan( ) ( ) ( ) ( )∂S ∂S ∂P ∂VT = T + T, (4.66)∂T P ∂T V ∂T V ∂T Pmissä C P ja C V ovat identifioitavissa yhtälöiden (4.60) ja (4.58) mukaisesti.Aputulos (A.5) (katso liite A) antaa osittaisderivaattojen välille relaation( ) ( ) ( )∂P ∂T ∂V= −1.∂T ∂V ∂PSijoittamalla tästä(∂P/∂T) V yhtälöön (4.66) saadaanVC P = C V − TMääritellään tilavuuden lämpölaajenemiskerroinα P ≡ 1 ( ) ∂VV ∂Tja isoterminen kokoonpuristuvuusκ T ≡ − 1 VNäiden avulla yhtälö (4.67) tulee muotoonPT[( ) ] ∂V 2/ ( ) ∂V. (4.67)∂T P ∂P TP(4.68)( ) ∂V. (4.69)∂P T,NC P − C V = TV α2 Pκ T. (4.70)Koska lämpölaajenemiskerroin ja isoterminen kokoonpuristuvuus ovat positiivisialukuja, on C P > C V aina. Laskemalla α P ja κ T ideaalikaasulle helpostitodetaan, että C P,id − C V,id = k B N.

58 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖMääritelmistä (4.60) ja (4.58) lämpökapasiteettien suhde onC PC V=Toisaalta tuloksen (A.5) avullajajoten( ) ∂S= −∂TP( ) ∂S= −∂T VC PC V=( ) ∂S∂T P( ) ∂S∂PT( ) ∂V∂T S( ) ( )∂S ∂V∂P T ∂S( ) ( )T∂T ∂V∂P ∂TMääritellään adiabaattinen kokoonpuristuvuusSκ p ≡ − 1 V/ ( )∂S.∂T VS/ ( )∂T∂PS/ ( )∂V,∂S T( ) ∂V∂P T= ( ) . (4.71)∂V∂PS( ) ∂V. (4.72)∂P S,NAdiabaattinen kokoonpuristuvuus määrää äänen nopeuden väliaineessa:c p =1√ mρκp, (4.73)missä m on hiukkasen massa ja ρ = N/V. Isotermisen ja adiabaattisen kokoonpuristuvuudenavulla yhtälö (4.71) voidaan kirjoittaa muotoonC PC V= κ Tκ p. (4.74)Yhtälöt (4.70) ja (4.74) ovat merkittäviä siksi, että ne ilmaisevat lämpökapasiteettienriippuvuussuhteen mitattavien suureiden avulla.4.10 Termodynamiikan kolmas pääsääntö (5.8)Vuonna 1906 Walther Nernst (1864–1941) muotoili kvanttimekaniikasta tehtyjenhavaintojen pohjalta lain, jonka mukaan entropian muutokset reversiibeleissäprosesseissa häviävät, kun lähestytään absoluuttista nollapistettä:lim ∆S = 0. (4.75)T→0

4.11. TERMODYNAMIIKAN PÄÄSÄÄNNÖT: SUPPEA KOOSTE 59Tämä ns. Nernstin laki tunnetaan usein termodynamiikan kolmantenapääsääntönä. Se on saanut pääsäännön aseman siksi, että se ei ole johdettavissaensimmäisestä ja toisesta pääsäännöstä.Planck esitti kolmannesta pääsäännöstä hieman vaativamman muodon:lim S = 0, (4.76)T→0jonka mukaan myös entropian absoluuttinen arvo menee nollaan, kun T → 0.Jos entropia käsitetään aineen järjestyksen mittana, on yhtälön (4.76) vaatimusjärkevä: absoluuttisessa nollapisteessä aine on täysin järjestynyt, eikä entropiavoi enää pienetä. Kuitenkin, jos makroskooppinen määrä aineen molekyylejämiehittää alinta energiatilaa kun T = 0, ei entropia tarkkaan ottaen voi ollanolla. Eräät aineet voivat myös jäädä hyvin pitkäikäiseen metastabiiliin tilaan,jossa entropia ei saavuta alinta arvoaan.Termodynamiikassa kolmannella pääsäännöllä on sopimusluonteinen asema,mutta tilastollisessa mekaniikassa se voidaan perustella mikroskooppisestanäkökulmasta.4.11 Termodynamiikan pääsäännöt: suppea koosteHyvin lyhyesti ilmaistuna termodynamiikan pääsäännöt ovat seuraavat:• Nollas pääsääntö: Jos kaksi kappaletta on erikseen termodynaamisessatasapainossa kolmannen kanssa, ovat ne tasapainossa myös keskenään.• Ensimmäinen pääsääntö: Energia säilyy.• Toinen pääsääntö: Lämpö ei siirry spontaanisti alemmasta lämpötilastakorkeampaan lämpötilaanVaihtoehtoisesti: Suljetun systeemin entropia maksimoituu tasapainotilassa.• Kolmas pääsääntö: Lähestyttäessä absoluuttista nollapistettä entropianmuutokset reversiibeleissä prosesseissa häviävät.Lukijan on erityisesti pidettävä mielessä, että varsinkin toisella pääsäännölläon useita keskenään ekvivalentteja muotoja, ja tässä on lueteltu vain lyhyet,epätäsmälliset muistisäännöt.4.12 Pisaran tarina, osa 1: taustaa ja tasapainoehdottermodynamiikan toisen pääsäännön avulla(˜8.8)4.12.1 Pisaranmuodostus ja ilmakehäIlma jota hengitämme on monimutkainen kokonaisuus kaasuja sekä kiinteitäja nestemäisiä hiukkasia, joista viimeisiä kutsutaan myös pisaroiksi, erityisesti

60 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖjos ne ovat kooltaan suuria, halkaisijaltaan satoja nanometrejä tai enemmän.Kaasumolekyylejä on kuutiosenttimetrissä 10 19 kappaletta, nestemäisiä taikiinteitä hiukkasia tyypillisesti muutamia tuhansia. Hiukkaset vaikuttavat ilmakehänsäteilytasapainoon suoraan sirottamalla ja absorboimalla auringonvaloa ja maasta tulevaa lämpösäteilyä. Vielä merkittävämpi on hiukkastenepäsuora vaikutus, sillä ne toimivat pilvien tiivistymisytiminä. Jokaisessa pilvipisarassaon paitsi vettä, myös pieni määrä muuta ainetta, alkuperäinenhiukkanen, jonka pinnalle vesi tiivistyy. Maan ilmakehän olosuhteissa pilvipisaroitaei muodostu ilman hiukkasia. Tiivistymisytimiksi tarjolla olevien hiukkastenlukumäärä ja ominaisuudet vaikuttavat pilvien ominaisuuksiin, esimerkiksisiihen kuinka valkoisia ne ovat, satavatko pilvet, ja jos niin kuinka pianjälkeen. Hiukkaset voivat sekä lämmittää että viilentää ilmastoa riippuen siitämissä kohtaa ilmakehää ne ovat ja millaisia ne ovat, mutta kaikkien hiukkastenkokonaisvaikutus on viilentävä. Paitsi ilmastoon ja säähän , hiukkaset vaikuttavatkeskeisesti myös ilmanlaatuun ja näkyvyyteen. Ilmansaasteiden uskotaanolevan suora syy noin 2,5 miljoonan ihmisen kuolemaan vuosittain, jailmakehän pienhiukkasten osuus tästä on 2,1 miljoonaa. Pienimmät hiukkasettunkeutuvat syvälle keuhkoihin ja jopa verenkiertoon asti. Erityisen vaikeatilanne on tällä hetkellä Itä- ja Etelä-Aasiassa, mutta historiallisesti Euroopassakinon ollut vaikeita ilmanlaatuongelmia, esimerkiksi Lontoon savusumu jaRuhrin alueen huono ilmanlaatu ovat tästä tunnettuja esimerkkejä.Ilmakehän pienhiukkasia tuottavat sekä luonnolliset että ihmisen toimintaanliittyvät prosessit. Osa hiukkasista on päässyt ilmakehään valmiina hiukkasina,esimerkkeinä polttoprosessien nokihiukkaset, aavikko- ja siitepöly sekämerisuola, joka jää jäljelle kun merivesipisarasta haihtuu vesi. 1990-luvun alussauskottiin, että mikäli ilmaan pääsee tiivistymiskykyisiä kaasuja (eli höyryjä)ne tiivistyvät näiden ilmaan suoraan päässeiden hiukkasten pinnalle. Kutentermodynamiikan ensimmäisen pääsäännön esittelyn yhteydessä kappaleessa3.1 todettiin, neste-kaasu tai kiinteä-kaasu rajapinnan muodostaminen vaatiienergiaa. Koska ilmakehässä on kaikkialla hiukkasia, joilla on jo pinta, tämänkiinteä-kaasu tai neste-kaasu pinnan kasvattamisen ja muuttamisen toisenlaiseksineste/kiinteä-kaasupinnaksi höyryjen tiivistyessä pitäisi olla energeettisestiedullisempaa kuin aivan uuden hiukkasen tai pisaran muodostaminen.Ilmakehän monimutkaisen kemiallisen koostumuksen vuoksi tämä asia ei kuitenkaanole näin yksinkertainen. Viimeisen 20 vuoden kuluessa on selvinnyt, että merkittävä ja mahdollisesti suurin osa ilmakehän hiukkasista on syntynytkokonaan höyryistä. Muodostumiseen osallistuvia höyryjä ja hiukkasmuodostusmekanismejailmakehän erilaisissa olosuhteissa ei kuitenkaan tunneta.Eniten käytetty ja yksinkertaisin teoria ilmakehän hiukkas- ja pilvipisaramuodostuksenymmärtämiseksi on nestepisaramalli, joka perustuu klassiseentermodynamiikkaan. Seuraavassa johdamme ensin tasapainoehdon btasomaiselleneste-kaasu rajapinnalle, ja sitten pallomaisen pisaran ja kaasun rajapinnalle.Jälkimmäinen tapaus antaa eväät ennustaa, minkä kokoinen pisara ontasapainossa (eli ei kasva eikä kutistu), jos höyryn laatu, tiheys ja lämpötilatunnetaan. Tästä voidaan edelleen ennustaa erikokoisten pisaroiden muodostumistodennäköisyyksiäerilaisissa olosuhteissa.

4.12. PISARAN TARINA, OSA 1: TAUSTAA JA TASAPAINOEHDOTTERMODYNAMIIKAN TOISEN PÄÄSÄÄNNÖN AVULLA (˜8.8) 614.12.2 Tasopinnan faasitasapainoTarkastellaan ensin lämpöeristettyä, jäykkää laatikkoa (eristetty systeemi) jossaon nestettä n ja kaasua k. Kaasua, joka kyseisessä lämpötilassa voi esiintyämyös nesteeksi tiivistyneenä, kutsutaan höyryksi. Esimerkiksi kaasufaasissaolevaa vettä huoneenlämpötilassa kutsutaan vesihöyryksi. Ilman typpeä sensijaan ei normaaliolosuhteissa kutsuta typpihöyryksi, koska sen nestemäiseenolomuotoon saattaminen vaatii hyvin kylmiä lämpötiloja. Tässä käytämme sanoja“kaasu” ja “höyry” toistensa synonyymeinä. Tarkastellaan yleistä tapausta,jossa kaasu ja neste koostuvat useasta molekyylityypistä i. Eri olomuotojaerottaa tasopinta jonka pinta-ala on A, pinta-ala pysyy vakiona dA = 0.Kuva 4.15: Neste- n ja kaasufaasit k joita erottaa tasopinta lämpöeristetyssä,jäykässä laatikossa.Systeemi koostuu itse asiassa tarkasti ottaen kolmesta osasta: neste n, kaasu(tai höyry) k ja niiden välinen rajapinta p. Faasin n(k) energia on U n(k) , entropiaS n(k) ja molekyylityypin i lukumäärä faasissa n(k) on N i,n(k) . Olomuodonn(k) tilavuus on V n(k) . Rajapinta sisältää energian U p , entropian S p , ja molekyylimäärätN i,p , Rajapinnan tilavuus on nolla ja pinta-ala A. Tutkitaan reversiibelejäprosesseja joissa rajapinta liikkuu ylös- tai alaspäinPinnan p energia muuttuu tällöin määrän ( käyttäen yhtälöä 3.5)kaasufaasin k energia muuttuuja nestefaasin n energian muutos ondU p = T p dS p + σdA+∑ µ i,p dN i,p ,idU k = T k dS k − P k dV k + ∑ µ i,k dN i,ki

62 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖdU n = T n dS n − P n dV n + ∑ µ i,n dN i,n .iNäistä yhtälöistä voidaan ratkaista entropian muutokset ja saadaandS p = 1 ( )dUp − σdA−T p∑ µ i,p dN i,pidS k = 1 ( )dUk + PT k dV k −k∑ µ i,k dN i,kidS n = 1 ( )dUn + P n dV n −T n∑ µ i,n dN i,n .iSysteemin kokonaisnentropian muutos on edellisten kolmen termin summadS tot = dS p + dS k + dS n .Etsimme tasapainotilaa, joka suljetussa systeemissä on entropian maksimiS tot = S tot,max ja reversiibelille prosessille dS tot = 0. Miksi tasapainossa ei pädeerikseen dS p = dS k = dS n = 0? Koska faasit voivat vaihtaa energiaa ja hiukkasiakeskenään, mutta koko systeemi on eristetty ulkomaailmasta Kun etsimmeentropian maksimia, täytyy pitää mielessä seuraavat reunaehdot:1. Kokonaisenergia säilyydU tot = dU p + dU k + dU n = 0 ⇒ dU p = −(dU k + dU n ).2. Kokonaistilavuus säilyydV tot = dV k + dV n = 0 ⇒ dV n = −dV k .3. Molekyylien kokonaislukumäärät säilyvätdN i,tot = dN i,p + dN i,k + dN i,n = 0 ⇒ dN i,p = −(dN i,k + dN i,n ).4. Faasien rajapinnan pinta-ala pysyy vakionadA = 0.Kun nämä ehdot sijoitetaan kokonaisentropian muutokseendS tot =( 1− 1 ) ( 1dUT k T k + − 1 ) (PkdU n +p T n T p(µi,k− ∑ − µ )i,pdNTi k T i,k −p∑i(µi,nT nT k− P nT n)dV k− µ i,pT p)dN i,n .(4.78)

4.12. PISARAN TARINA, OSA 1: TAUSTAA JA TASAPAINOEHDOTTERMODYNAMIIKAN TOISEN PÄÄSÄÄNNÖN AVULLA (˜8.8) 63Seuraavaksi käytetään termodynamiikassa erittäin tavallista päättelyä. Jotta oltaisiinmaksimikohdassa dS tot täytyy olla nolla kaikkiin suuntiin liikuttaessa.Jos muutamme energiaa U k , mutta pidämme U n , V k , N i,k ja N i,n vakioina dS tottäytyy olla nolla. Tästä seuraa( 1dS tot = − 1 )dUT k T k ,pdU k ̸= 0 → T k = T p .Samalla tavalla, jos muutamme vain energiaa U n , saammeT n = T p (= T k ). (4.79)ottamalla muutettavaksi yhden muuttujan kerrallaan muiden pysyessä vakioina,saammemuutetaan tulosV k :P k=T P n⇒ Pk T k = P n n(4.80)N i,k : µ i,k = µ i,pN i,n : µ i,n = µ i,p (= µ i,k ) (4.81)Huomaa, että ‘kaikkien suuntien järkeily´ on mahdollista vain kun kaikkiesiintyvät muuttujat U k , U n , V k , N i,k ja N i,n ovat riippumattomia: yhtä niistävoidaan muuttaa muuttamatta mitään muita. Kaikki reunaehdot täytyy siksiolla otettu huomioon ennen muotoa (4.78). Esimerkiksi muuttujajoukko U k ,U n , V k , V n , N i,k ja N i,n ei ole toisistaan riippumaton. Joko V k tai V n täytyy lausuatoisen avulla ennenkuin ‘kaikkien suuntien järkeilyä´ voidaan käyttääLopputulos on, että kaikkien aineiden kemiallisten potentiaalien jalämpötilan täytyy olla sama kaikissa faaseissa, myös pintafaasissa, ja paineentäytyy olla sama kaasussa ja nesteessä, kun niitä erottaa tasopinta.Yleispätevästi lämpötilan on aina oltava sama kaikissa faaseissa, muutenlämpö virtaa ja ei ole kyse tasapainosta. Kemiallisten potentiaalien on oltavasamat, muuten hiukkaset virtaavat. Paineen ei sen sijaan tarvitse olla samakaikkialla tasapainosysteemissä kuten pian näemme.hKuva 4.16: Kaaviokuva vesilasista.Huom: Usein faasitapainosta puhuttaessa todetaan virheellisesti, että paineenkinon oltava sama kaikkialla systeemissä. Vesilasi toimii vastaesimerkkinä(4.16)

64 LUKU 4. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖHydrostaattinen paine syvyydellä h on nesteessä, jonka tiheys on ρ onP = ρg grav h+ P ilmakehä , missä g grav on gravitaatiokiihtyvyys. Tämä on kuitenkintasapainosysteemi, jos lämpötila kaikkialla lasissa on sama. Mikään eivirtaa. Ajasta riippumaton voimakenttä (gravitaatio) aiheuttaa paine-eroja systeemieneri osien välille. Ilmapylväs maan ilmakehässä sen sijaan ei ole tasapainosysteemi,koska lämpötila ei ole sama kaikkialla pylväässä, ja esiintyylämmön virtausta.4.12.3 Pisaran faasitasapainoTarkastellaan nyt tapausta, missä faaseja erottaa pallopinta.Kuva 4.17: Neste- n ja kaasufaaseja k erottaa pallopinta, jonka pinta-ala on A.Systeemi on lämpöeristetyssä ja jäykässä laatikossa.Tilavuudet ja faasien välisen rajapinnan pinta-ala ovat kytkettyjä toisiinsa geometristenyhteyksien vuoksi: Pallon säde on r, ja sen pinta-ala on A = 4πr 2 .Kun säde muuttuu infinitesimaalisen määrän dr, pinta-alan muutos on dA =8πrdr. Pallon tilavuus eli nestefaasin tilavuus on V n = 4 3 πr3 , ja tämän tilavuudenmuutos säteen muuttuessa määrän dr on dV n = 4πr 2 dr. Etenemme samallatavalla kuin johdettaessa yhtälöä (4.78) kokonaisentropian muutokselle.Ainoa ero tulee sitä, että nyt meidän on otettava huomioon pinta-alan muutoksestajohtuva termi − σ T pdA pinnan energiassa, joten

4.12. PISARAN TARINA, OSA 1: TAUSTAA JA TASAPAINOEHDOTTERMODYNAMIIKAN TOISEN PÄÄSÄÄNNÖN AVULLA (˜8.8) 65dS tot =( 1− 1 ) ( 1dUT k T k + − 1 )dU nk T n T p(Pk+ − P )ndVT k T k −n∑(µi,n− ∑Ti n= 0 tasapainossai(µi,kT k− µ i,pT p)dN i,n − σ T pdA− µ i,pT p)dN i,k(4.83)Nyt on tärkeää huomata, ettemme vielä ole käyttäneet kaikkia reunaehtoja ja tilavuudetV k on vielä kytköksissä pinta-alaanA : Systeemin kokonaistilavuudensäilymisestä dV k + dV n = 0 seuraa dV k = −dV n = 4πr 2 dr ja pinta-alan muutosdA = 8πrdr voidaan ilmaista tilavuuden muutoksen avulla dA = 2dV nr . Kuntämä sijoitetaan yhtälöön (4.83) saadaandS tot =( 1− 1 ) ( 1dUT k T k + − 1 )dU nk T n T p(µi,k+ ∑Ti k− µ i,pT p)dN i,k(µi,n+ ∑ − µ )i,pdNTi n T i,np(Pk− − P n+ 2σ )dV nT k T n T p r= 0 tasapainossa.Nyt (mutta vasta nyt!) voimme käyttää ‘kaikkien suuntien järkeilyä´ ja saadatasapainoehdot (4.79) ja (4.81) lämpötilalle ja kemialliselle potentiaalilleja paineille uusi ehtojoka johtaa Laplacen yhtälöönT k = T n = T p , (4.84)µ i,k = µ i,n = µ i,p (4.85)P kT k− P nT n+ 2σT p r = 0P n = P k + 2σ r . (4.86)Paine pisaran sisällä on suurempi kuin ympäröivässä kaasussa (olettaenettä pintajännitys σ > 0). Tämä paine-ero tuottaa ulospäin suuntautuvan voiman,joka vastustaa pintajännityksestä johtuvaa voimaa, joka puolestaan suuntautuusisäänpäin ja pyrkii kutistamaan pisaraa.

Luku 5Termodynaamiset potentiaaliteli vapaat energiat5.1 Systeemin sisäistä tilaa kuvaavat muuttujatTähän mennessä olemme käsitelleet tasapainoehtoja vain suljetuissa systeemeissä,joissa U, V, N i ovat vakioita. Tasapainotila löydetään maksimoimallaentropia S = S max . Maksimointi tehdään muiden systeemin sisäistä tilaa kuvaavienparametrien x(, y, ...) suhteen pitäen energia U(x, ...), tilavuus V(x, ...)ja hiukkasmäärät N i (x, ...) vakioina. x voi olla esimerkiksi liikkuvan väliseinänpaikka kuvassa 5.1.Kuva 5.1: Suljettu systeemi, jonka sisällä liikkuva väliseinä erottaa kaksi erilaistakaasua toisistaan.

5.2. YMPÄRISTÖN KANSSA VUOROVAIKUTTAVAT SYSTEEMIT (5.7, 6.1) 67Lämpöeristetyssä jäykässä laatikossa kokonaisenergia U tot , kokonaistilavuusV tot ja kokonaishiukkasmäärät N i,tot ovat vakioita.U tot = U 1 + U 2N i,tot = N i,1 + N i,2V tot = V 1 + V 2 .Etsimällä entropian S maksimi väliseinän paikan x suhteen löydämmeväliseinän tasapainosijainnin. Reversiibelissä prosessissa jossa U tot , V tot ja N i,totovat vakioita entropia on myös vakio, koska dS tot = 0.5.2 Ympäristön kanssa vuorovaikuttavat systeemit(5.7, 6.1)Mitä jos joitakin muita tilamuuttujia kuin energiaa, tilavuutta ja hiukasmääriäpidetäänkin vakioina? Intensiiviset tilamuuttujat paine P, lämpötila Tja kemiallinenpotentiaali µ i voidaan pitää vakioina kytkemällä systeemi kylpyyn,jonka kanssa systeemi vaihtaa vastaavasti tilavuutta ∆V, lämpöä ∆Q ja hiukkasia∆N i . Kylpy on tasapainotilassa oleva systeemi, joka on paljon suurempikuin meidän tarkastelemamme varsinainen systeemi. Kylvyn intensiivisetominaisuudet (P 0 , T 0 , µ i,0 ) eivät suuren koon vuoksi muutu, vaikka kylpyvaihtaa tilavuutta, lämpöä tai hiukkasia systeemin kanssa. Kylvyn ekstensiivisetominaisuudet (V 0 , N i,0 , S 0 ja U 0 ) tietenkin muuttuvat, mutta suhteellisestiottaen hyvin vähän eli ∆V 0 /V 0

68 LUKU 5. TERMODYNAAMISET POTENTIAALIT ELI VAPAAT ENERGIATKuva 5.2: Systeemin ja kylvyn muodostama yhdistetty systeemi on suljettu.Systeemi on paljon pienempi kuin kylpy.kokonaisentropia pysyy vakiona tai kasvaa, dS tot ≥ 0 (dS tot = 0 vain reversiibeleilleprosesseille).Systeemin ja kylvyn entropioiden avulla lausuttuna tästä saadaandS tot = dS+dS 0 ≥ 0.Kylvyn prosessit ovat aina reversiibeleitä, joten kylpyyn virtaavalle lämpömäärälleja kylvyn tekemälle työlle päteed - Q 0 = T 0 dS 0 ,d - W 0 = P 0 dV 0 .Kirjoitetaan kylvyn entropian muutos ylläolevan reversiibelin tapauksen kaavanavulla, jolloin saadaan kokonaisentropian muutokselledS tot = dS+dS 0 = dS+ d- Q 0T 0= dS− d- QT 0. (5.1)Säilymislait kertovat, että kaiken mikä lähti systeemistä, täytyy päätyä kylpyynja päinvastoin:Lämpövirtojen tasapaino: lämpö d - Q jokasysteemiin virtaa täytyy lähteä kylvystä.Kylpyyn virtaava lämpömäärä•on siten d - Q 0 = −d - QdQdQ 0

5.2. YMPÄRISTÖN KANSSA VUOROVAIKUTTAVAT SYSTEEMIT (5.7, 6.1) 69Systeemin tekemä työ d - W päätyy kylpyyn.•Kylvyn tekemä työ on siis d - W 0 =−d - WdWdW 0Kokonaistilavuus säilyy:Systeemin tilavuuden muutoksen ollessadV kylvyn tilavuuden muutos on•dV 0 = −dV.Hiukkaset jotka tulevat systeemiinlähtevät pois kylvystä dN i = −dN i,0 .dN• Hiukkasten kylpyyn kuljettama energialähtee pois systeemistädN i,0iµ i dN i = −µ i,0 dN i,0Termodynamiikan ensimmäinen pääsääntö systeemille ondU = d - Q−d - W+ ∑ µ i dN i ,ijosta ratkaistaan systeemiin tuleva lämpömääräd - Q = dU+ d - W − ∑ µ i dN ijoka voidaan edellä lueteltujen säilymislakien avulla lausua muodossad - Q = dU− d - W 0 + ∑ µ i,0 dN i,0 .Kylvyn tekemälle työlle voidaan käyttää reversiibeliä kaavaad - Q = dU−P 0 dV 0 + ∑ µ i,0 dN i,0 ,jonka jälkeen palataan systeemin tilavuuden ja hiukkasmäärien muutoksiinsäilymislakien avullad - Q = dU+P 0 dV− ∑ µ i,0 dN i .Kun tämä sijoitetaan termodynamiikan toiseen pääsääntöön (5.1), saadaandS tot = dS−dU+P 0 dV− ∑ µ i,0 dN ii≥ 0.T 0Kerrotaan tämä epäyhtälö kylvyn lämpötilalla T 0 ̸= 0T 0 dS−dU−P 0 dV+ ∑ µ i,0 dN i ≥ 0isiirretään kaikki termit epäyhtälön toiselle puolelle, jolloin saadaan Clausiuksenepäyhtälö muodossadU−T 0 dS+ P 0 dV− ∑ µ i,0 dN i ≤ 0. (5.2)i

70 LUKU 5. TERMODYNAAMISET POTENTIAALIT ELI VAPAAT ENERGIATTässä T 0 , P 0 , µ i,0 ovat kylvyn ominaisuuksia ja U, S, V, N i systeemin ominaisuuksia.Merkitään lyhyyden vuoksidϕ = dU−T 0 dS+ P 0 dV − ∑ µ i,0 dN i .iToisen pääsännön muodon dS ≥ 0 sijasta meillä on kylvyn kanssa energiaa jahiukkasia vaihtavalle systeemille dϕ ≤ 0, jonka täytyy päteä kaikille spontaaneilleprosesseille. Tasapainossa mikään spontaani prosessi ei ole mahdollinen,ϕ ei voi siis pienentyä, joten tasapainoa vastaa ϕ:n minimi ( tietyillä kiinnitetyilläarvoilla T 0 , P 0 , µ i,0 ). Saamme valita minkä tahansa funktion ϕ jonka differentiaalion dϕ = dU−T 0 dS+ P 0 dV − ∑ i µ i,0 dN i ja tämän vapaan energian ϕminimi on tasapainotila.Jos kytkentä ympäristöön on sellainen, että systeemin entropia, tilavuus jahiukkasmäärä säilyvät vakioina dS = dV = dN i = 0, Clausiuksen epäyhtälötulee muotoon dϕ = dU ≤ 0, ja voimme valita vapaaksi energiaksi sisäisenenergian ϕ = U. Tällöin tasapainoa vastaa energian minimi Miten entropianarvo sitten pidetään vakiona? Jos systeemille sallitaan vain reversiibelitmuutokset, tämä tarkoittaa lämpöeristystä, mutta irreversiibeleitä prosessejaläpikäyvälle systeemille käytännöllistä keinoa ei ole. Mekaniikassa tasapainotilaon myös energian minimi: voima on energian derivaatta, ja kun derivaattaon nolla, voima on nolla, ja kappale pysyy kyseisessä tilassa (jonka määritteleeesimerkiksi paikka ja nopeus).Jos kytkentä pitää vakiona tilavuuden ja hiukkasmäärän V, N i , mutta salliilämpövuon kylvystä/kylpyyn jonka lämpötila on T 0 , Clausiuksen epäyhtälötulee muotoondϕ = dU−T 0 dS ≤ 0ja voimme valita vapaaksi energiaksi funktionϕ = U−T 0 S.Tarkistetaan, että vapaan energian ϕ differentiaali antaa oikean tuloksen: yleisestiottaendϕ = dU−T 0 dS+SdT 0 ,mutta koska lämpötila oli vakio dT 0 = 0, saadaandϕ = dU−T 0 dS,kuten pitääkin. Tällaiselle systeemille tasapainotila löydetään etsimällä Helmholtzinvapaan energian F minimi, missäF = U−T 0 SReversiibelissä prosessissa, jossa vakiona pidetään T = T 0 , V ja N i on Helmholtzinvapaa energia vakio dF = 0, sillä olemme aina infinitesimaalisen lähellätasapainotilaa.

5.2. YMPÄRISTÖN KANSSA VUOROVAIKUTTAVAT SYSTEEMIT (5.7, 6.1) 71Taulukko 5.1: Yhteenveto kaikista tavallisesti käytetyistä vapaista energioistaeli termodynaamisista potentiaaleista.yleensävakiot reversiibelissäproses-epäyhtälön muo-Clausiuksenvapaasti vaihdettavasuurekäytetty ϕjonka minimisissato dϕ < 0on tasapainotilaU, V, N i −T 0 dS ≤ 0 ⇒ dS ≥ 0 S Entropia (max!)S, V, N i dU ≤ 0 U (Sisäinen) energiaT = T 0 , V, N i lämpö dU−T 0 dS ≤ 0P = P 0 , T = T 0 ,N ilämpö, tilavuus dU−T 0 dS+ P 0 dV ≤ 0F = U−T 0 SHelmholtzinvapaaenergiaG = U−T 0 S+P 0 VGibbsin vapaaenergiaS, P = P 0 , N i tilavuus dU+P 0 dV ≤ 0 H = U+P 0 VEntalpiaT = T 0 ,µ i = µ i,0 , Vlämpö, hiukkaset dU−T 0 dS−∑µ i,0 dN i ≤ 0Ω = U−T 0 S−∑ µ i,0 N iSuuri potentiaaliKaikki tavallisimmin käytetyt termodynaamiset potentiaalit on koottu taulukkoon5.1. Huomaa, että ekstensiivisten suureiden V, N i , U, ja S vakionapitämiseksi täytyy rakentaa seinämiä jotka eivät liiku, läpäise hiukkasia ja/tailämpöä, mutta intensiivisten suureiden P, µ i ja T vakiona pitämiseksi täytyytaata seinämien vapaa liikkuvuus tai esteettömät hiukkas- ja/tai lämpövuot.Vapaat energiat ovat systeemiä ja kylpyä yhdessä kuvaavia apufunktioita.Voisimme aina tarkastella systeemin ja kylvyn muodostamaa kokonaisuuttaja soveltaa termodynamiikan toista pääsääntöä sen “entropian maksimi ontasapainotila” - muodossa. Käytettäessä vapaita energioita työ on tehty puoleenväliin, eli kylvyn, jolla on standardiominaisuudet, osuus on häivytettylähes kokonaan. Vain kylvyn relevantit intensiiviset ominaisuudet P 0 , µ i,0 ,T 0 näkyvät taulukon 5.1 vapaissa energioissa. Minimoimalla sopivaa vapaataenergiaa tulokset saadaan suoraviivaisemmin kuin aloittamalla aina alustakokonaissysteemin (systeemi+ kylpy) entropian maksimoinnista.

72 LUKU 5. TERMODYNAAMISET POTENTIAALIT ELI VAPAAT ENERGIAT5.3 Vapaat energiat ja niiden tasapainoarvojen derivaatat(2.9, 2.10, 6.2)Jos systeemi on kytketty kylpyyn, jota karakterisoi jokin osajoukko muuttujistaP 0 , T 0 ja µ i,0 , sen sisäiset muuttujat, kuten molekyylien järjestys tai jakautuminensysteemin eri osiin tai liikkuvien sisäisten väliseinien paikka, asettuvattasapainoarvoihin, jotka minimoivat vapaan energian, joka saa tasapainossaarvon ϕ eq . Tämä arvo riippuu kuitenkin kylvyn parametreistä P 0 , T 0 ja/taiµ i,0 ja kussakin tapauksissa systeemin vakiona pysyvistä ekstensiivisistä ominaisuuksista(V, N i , S ). Tutkitaan nyt miten vapaan energian tasapainoarvomuuttuu, kun olosuhteita P 0 , T 0 ja/tai µ i,0 ja systeemin ominaisuuksia V, N i , Smuutetaan.5.3.1 Helmholtzin vapaa energiaLämpökylpyyn (jonka lämpötila T 0 ) kytketylle systeemille:ϕ eq = F eq = U−T 0 S,josta saadaandF eq = dU−T 0 dS−SdT 0 .Reversiibeleille muutoksille dU = TdS− PdV + ∑ µ i dN i , joten dF eq = TdS−PdV+ ∑ µ i dN i − T 0 dS−SdT 0 .Tasapainossa systeemin lämpötila on sama kuin kylvyn T = T 0 , josta seuraadF eq = −SdT 0 − PdV+ ∑ µ i dN i .Tämä kertoo, miten Helmholtzin vapaan energian tasapainoarvo muuttuu,kun systeemin reunaehtoja T 0 , V ja N i muutetaan. Useimmiten tasapainoonviittaava alaindeksi eq samoin kuin kylvyn ominaisuuksiin viittaava alaindeksi0 jätetään pois, ja näin teemme jatkossa, mutta edellä sitä on käytetty korostamaansitä mistä muutoksessa on kyse.Tuloksesta saadaan kemialliselle potentiaalille vaihtoehtoinen määritelmä,jossa hiukkasen lisäyksessä vakiona pidetään lämpötilaa ja tilavuutta epäkäytännöllisenentropian sijaan, joka esiintyy määritelmässä (4.7.3)µ i =( ∂F∂N i)T,V,N i̸=j. (5.3)Helmholtzin vapaan energian differentaalista saamme lisäksi identifikaatiotS = −( ) ∂F,∂T V,N iP = −( ∂F∂V)T,N i. (5.4)

5.3. VAPAAT ENERGIAT JA NIIDEN TASAPAINOARVOJEN DERIVAATAT(2.9, 2.10, 6.2) 73jolloin toisista derivaatoista saamme Maxwellin relaatiot( ) ( )∂S∂P=, (5.5)∂V T,N i∂T V,N( ) ( ) i∂S∂µ= − , (5.6)∂N i T,V,N j̸=i∂T V,N i( ) ( )∂P∂µ= − . (5.7)∂N i ∂V T,N iT,VN j̸=iLämpötila, tilavuus ja hiukkasmäärä ovat koetilanteessa helposti kiinnitettäviäsuureita. Sen vuoksi Helmholtzin vapaalla energialla on paljon käyttöäfysiikassa ja kemiassa. Se on myös keskeinen suure tilastollisessa mekaniikassa.Luonnollisten muuttujien käsite liitetään useimmiten juuri termodynaamisiinpotentiaaleihin eli tyyppisiin vapaisiin energioihin (vapaan energian käsitetässä tapauksessa sisältää entropian ja sisäisen energian). Termodynaamistenpotentiaalien kyseessä ollessa luonnolliset muuttujat määräytyvät kahdellavaihtoehtoisella tavalla, jotka ovat yhtäpitävät, eli aina seuraa sama muuttujienjoukko kullekin potentiaalille, käytti kumpaa ’ehtoa’ tahansa:A) ne muuttujat, joiden vakiona ollessa kyseisen potentiaalin minimi (S:ntapauksessa maksimi) antaa termodynaamisen tasapainotilan, esimerkiksiHelmholtzin vapaalle energialle F nämä ovat T,V ja N i .B) jos tietty termodynaaminen potentiaali on lausuttu luonnollisten muuttujienavulla, termodynaamisen potentiaalin ja sen osittaisderivaattojen avullavoidaan laskea kaikki systeemin termodynaamiset ominaisuudet. Esimerkiksijos F on lausuttu muuttujien T,V ja N i avulla, tämä sisältää kaiken tarvittaessaolevan tiedon systeemin termodynamiikasta. Jos sinulla sen sijaan on lauseke,jossa F annetaan esimerkiksi muuttujien T, P ja N i avulla, tarvitaan lisäksiesimerkiksi tilanyhtälö, jotta systeemin kaikki termodynaamiset ominaisuudetvoidaan laskea.Tätä ei välttämättä näen mitenkään suoraan lausekkeesta, eli täytyy tietäämiten eri potentiaalit on määritelty, jotta osaisi tunnistaa luonnolliset muuttujat.’Peruskaavoista’, kuten dF = −SdT−PdV + ∑ i µ i dN i , ’näkyy suoraan’,että T,V ja N i ovat Helmholtzin vapaan energian luonnolliset muuttujat, muttatästä johdetusta muodosta dF = (PVα P + S)dT+PVκ T dP+∑ i µ i dN i ei voidakaanenää helposti päätellä mitään luonnollisista muuttujista.Gibbsin ja Duhemin yhtälöä (4.39) seurasi toteamus, että P ja T ovat kemiallisenpotentiaalin luonnolliset muuttujat. Tämän voi perustella siten, ettäjos P ja T ovat vakiot, µ on aina vakio (yksikomponenttisysteemissä). MuuttujienP, V, T ja N kuvaamalle systeemille tämä merkitsee että Vn ja N:n arvoillaei ole väliä, kunhan P ja T ovat vakioita, kemiallinen potentiaalikin on vakio.V ja T eivät ole yhtä hyvä pari määrittelemään kemiallista potentiaalia, sillävaikka V ja T olisivat vakioita, jos N ja P muuttuvat (molempien on muututtava,koska muuttujia V, T, P ja N sitoo tilanyhtälö ,eikä voi olla niin että esimV, T ja N ovat vakioita ja vain P muuttuu), kemiallinen potentiaali muuttuu.

74 LUKU 5. TERMODYNAAMISET POTENTIAALIT ELI VAPAAT ENERGIAT5.3.2 Gibbsin vapaa energiaSysteemille, joka on kytketty paine- ja lämpökylpyyn (lämpötila T 0 , paine P 0 ):jonka kokonaisdifferentiaali onϕ eq = G eq = U−T 0 S+ P 0 V, (5.8)dG eq = dU−T 0 dS−SdT 0 + P 0 dV+ VdP 0 .Tasapainossa systeemin paine ja lämpötila ovat samat kuin kylvyn P = P 0ja T = T 0 ja reversiibeleille muutoksille dU = TdS− PdV + ∑ µ i dN i , jotensaadaandG eq = −SdT 0 + VdP 0 + ∑ µ i dN i .Tämä kertoo, miten Gibbsin vapaan energian tasapainoarvo muuttuu, kun systeeminreunaehtoja T 0 , P 0 ja N i muutetaan.Kemialliselle potentiaalille saadaan nyt toinen vaihtoehtoinen määritelmä,jossa paine ja lämpötila pidetään vakiona hiukkasen lisäyksessä( ) ∂Gµ i =. (5.9)∂N i T,P,N j̸=iGibbsin vapaan energian differentiaalin muut kertoimet ovat( ) ( )∂G∂GS = − , V = . (5.10)∂T P,N i∂P T,N iGibbsin vapaaseen energiaan liittyvät Maxwellin relaatiot( ) ( )∂S∂V= − , (5.11)∂P T,N i∂T P,N( ) ( ) i∂S∂µ= − , (5.12)∂N i T,P,N j̸=i∂T P,N i( ) ( )∂V∂µ. (5.13)∂N i ∂P T,N iT,P,N j̸=i=Olomuodonmuutoksissa eli faasitransitioissa paine ja lämpötila pysyvätvakioina, mutta systeemien sisäinen järjestys muuttuu. Gibbsin vapaa energiaonkin sopiva termodynaaminen potentiaali faasitransitioiden tarkasteluun.Gibbsin funktiota käytetään usein fysiikassa ja kemiassa, koska T, P ja N i voidaanhelposti kiinnittää koejärjestelyin. Erityisen tärkeä Gibbsin vapaa energiaon ensimmäisen kertaluvun faasitransitioiden yhteydessä, koska ne tapahtuvatvakiopaineessa ja -lämpötilassa.Gibbsin vapaalle energialle saadaan mielenkiintoinen tulkinta, kun yhdenkomponentin fundamentaalinen yhtälö (4.38) sijoitetaan määritelmään (5.8)(lämpötilana T = T 0 ja paineena P = P 0 ):G = TS− PV + µN− TS+PV = µN

5.3. VAPAAT ENERGIAT JA NIIDEN TASAPAINOARVOJEN DERIVAATAT(2.9, 2.10, 6.2) 75eliµ = G/N. (5.14)Kemiallinen potentiaali yhden komponentin aineelle on siis Gibbsin vapaaenergia hiukkasta kohden.Tässä yhteydessä on syytä todeta, että muodosta G = µN ei voida identifioidasysteemin luonnollisia muuttujia (kuten ei myöskään vastaavalla tavallajohdettavista yhtälöistä muille termodynaamisille potentiaaleille). Voidaankirjoittaa (sinänsä oikein) dG = µdN + Ndµ, mutta µ ja N eivät yksin riitämääräämään systeemin tilaa.5.3.3 EntalpiaSysteemille joka on kytköksissä painekylpyyn P 0 :jonka kokonaisdifferentiaali onϕ eq = H eq = U+P 0 V,dH eq = dU+P 0 dV+ VdP 0 .Reversiibelille muutoksille systeemin paine on P = P 0 sekä dU = TdS− PdV+∑ µ i dN i , joten entalpian muutos ondH eq = VdP 0 + TdS+∑ µ i dN i .Tämä kertoo, miten entalpian tasapainoarvo muuttuu, kun systeemin reunaehtojaS, P 0 ja N i muutetaan.Entalpian differentiaalimuodosta voidaan identifioidaT =( ∂H∂S)P,N i, V =( ∂H∂P)S,N i, µ i =( ∂H∂N i)S,P,N j̸=i. (5.15)Näiden avulla saadaan kolme uutta Maxwellin relaatiota:( ) ( )∂T∂V=, (5.16)∂P S,N i∂S P,N( ) ( ) i∂T∂µ=, (5.17)∂N i S,P,N j̸=i∂S P,N i( ) ( )∂V∂µ. (5.18)∂N i ∂P S,N iS,P,N j̸=i=Entalpiaa kutsutaan myös lämpöfunktioksi, sillä vakiopaineessa tapahtuvissaprosesseissa entalpian muutos on yhtä suuri kuin siirtynyt lämpömäärä.Reversiibeliä tietä kuljettaessa nimittäin∆Q = ∆U+P∆V (5.19)

76 LUKU 5. TERMODYNAAMISET POTENTIAALIT ELI VAPAAT ENERGIATeli∆Q = U n − U a + P(V n − V a ) = U n + PV n −(U a + PV a ) = H n − H a = ∆H,(5.20)missä alaindeksit a ja n viittavaat alku- ja lopputiloihin.Lämpökapasiteetti vakiopaineessa voidaankin lausua entalpian avullaC p = (∂H/∂T) P = (d - Q/∂T) P . Entalpiaa tarvitaan mm. jatkuvan aineen mekaniikassa.Entalpian muutos kuvaa myös olomuodonmuutoksissa siirtyväälämpöä, ns. latenttia lämpöä.5.3.4 Suuri potentiaaliSysteemi joka on kytketty lämpö- ja hiukkaskylpyyn µ i,0 , T 0 :jonka kokonaisdifferentiaali onϕ eq = Ω eq = U−T 0 S−∑ µ i,0 N i , (5.21)dΩ eq = dU−T 0 dS−SdT 0 − ∑ µ i,0 dN i − ∑ N i dµ i,0 .Reversiibeleille muutoksille T = T 0 , µ i = µ i,0 , ja jälleen dU = TdS− PdV +∑ µ i dN i , jotendΩ eq = −SdT 0 − PdV− ∑ N i dµ i,0 .Tämä kertoo, miten suuren potentiaalin tasapainoarvo muuttuu, kun systeeminreunaehtoja T 0 , µ i,0 ja V muutetaan.Entropia, paine ja hiukkasmäärä saadaan suuren potentiaalin ensimmäisistäderivaatoistaS = −( ∂Ω∂T)V,µ i,P = −( ) ∂Ω,∂V T,µ i( ) ∂ΩN i = −, (5.22)∂µ i T,V,µ j̸=ija toisista derivaatoista johdetaan( ) ∂S∂V( ) ∂S∂µ i( ) ∂P∂µ iT,µ i=T,V,µ j̸=i=T,V,µ j̸=i=( ) ∂P, (5.23)∂T V,µ( )i∂Ni, (5.24)∂T V,µ i( ) ∂Ni. (5.25)∂V T,µ iSuuren potentiaalin luonnolliset muuttujat ovat T, V ja µ i . Suuri potentiaaliminimoituu, kun systeemi on asetettu hiukkaskylpyyn. Hiukkaskylvyssä systeeminseinät läpäisevät hiukkasia ja käytännössä myös lämpöä. Ympäristönkanssa vaihdettavat suureet ovat silloin hiukkasmäärä ja entropia. Hiukkaskylvyssäsysteemin seinät voidaan ajatella täysin kuvitteellisiksi eli systeemion avoin.

5.4. MIKSI TERMODYNAAMISIA POTENTIAALEJA KUTSUTAAN MYÖSVAPAIKSI ENERGIOIKSI? (6.1) 77P 1V 1P 2V 2FmKuva 5.3: Liikuteltavalla männällä kahteen osaan jaettu säiliö. Mäntä on kytkettypunnukseen.Suurelle potentiaalille saadaan fysikaalinen tulkinta fundamentaalisenyhtälön ja määritelmän (5.21) avulla:Ω = −PV. (5.26)Paine on siis etumerkkiä vailla suuren potentiaalin tiheys.Vanhemmissa termodynamiikan kirjoissa suurta potentiaalia ei välttämättäedes mainita. Suuri potentiaali on kuitenkin hyödyllinen eräissä termodynaamisissasovelluksissa ja erityisen keskeisessä asemassa se on tilastollisessa mekaniikassa.5.4 Miksi termodynaamisia potentiaaleja kutsutaanmyös vapaiksi energioiksi? (6.1)Tarkastelemme kaasua säiliössä, joka on jaettu liikuteltavalla männällä (pintaalaA) kahteen osaan kokonaistilavuuden V 1 + V 2 pysyessä vakiona (kuva 5.3).Mäntä liikkuu reversiibelisti. Voidaan kuvitella, että mäntä on kytketty kitkattomanväkipyörän välityksellä punnukseen (massa m). Jos P 1 A + mg >P 2 A, tekee massa kaasuun työtä ja voiman suunta on kuvan mukainen. Jostaas P 1 A+mg < P 2 A, kaasu tekee massaan työtä. Kun punnuksen korkeusmuuttuu dh verran, on mekaanisen energian muutos eli tehty työ d¯W =(P 1 A+mg− P 2 A)dh. Reversiibelissä muutoksessa ovat hetkelliset paineet kokoajan samat molemmilla puolilla väliseinää eli P 1 = P 2 , joten tehty työ ond¯W = mgdh, josta integroimalla saadaan ∆W = mg∆h.Ensimmäisen pääsäännön mukaan sisäisen energian muutos on∫∆U = ∆Q−∆W +µdN = ∆U = ∆Q−mg∆hmissä on oletettu, ettei säiliön kaasun ainemäärä muutu , ja kaasuun siirtynytlämpö on ∆Q. Punnuksen energian muutokset mg∆h ovat potentiaalienergianmuutoksia, jotka ovat kokonaisuudessaan palautettavissa systeemiin

78 LUKU 5. TERMODYNAAMISET POTENTIAALIT ELI VAPAAT ENERGIATtyön muodossa. Gravitaatiokentän puuttuessa samanlainen energian varastointimekaaniseen muotoon voidaan toteuttaa esimerkiksi kitkattoman jousenavulla.Reversiibelissä muutoksessa ∆Q = ∫ TdS. Pidetään esimeriksi säiliönlämpötila vakion, jolloin virrannut lämpö on ∆Q = T∆S. Ensimmäinenpääsääntö antaa tällöin(∆U−T∆S) T,V,N = −mg∆h ≡ −∆W vapaa . (5.27)Tämä tarkoittaa, että sellaisessa reversiibelissä prosessissa, jossa T, V ja N ovatvakioita, työ voidaan kokonaisuudessaan varastoida Helmholtzin vapaaseenenergian muutokseksi ∆F = ∆U−T∆S ja palauttaa takaisin työn muodossa.Irreversiibelissä prosessissa systeemin sisäiset spontaanit muutokset kasvattavatentropiaa. Clausiuksen epäyhtälön nojalla ∆Q irr < ∫ TdS. Siispä, kunlämpötila, kokonaistilavuus ja -hiukkasmäärä ovat vakioita, on voimassa(∆F) T,V,N < −∆W vapaa . (5.28)Irreversiibelissä tapauksessa sisäinen Helmholtzin vapaa energia ja työ eivätsiis ole täysin vaihtokelpoisia. Jos esimerkiksi kuvan 5.3 punnus laskee nopeasti,kuluu osa työstä kaasun sekoittamiseen männän liikkuessa.Muut vapaat energiat ovat samalla tavalla täysin vaihtokelpoisia työn kanssa,kunhan vain tietty joukko tilamuuttujia pysyy vakiona ja prosessi on reversiibeli.Koska minkä tahansa näistä energioista voi sopivien reunaehtojen vallitessavaihtaa vapaasti työksi ja takaisin, sanotaan niitä vapaiksi energioiksi.On hyvä huomata, että tässä olemme tarkastelleet vain yksinkertaista PTVsysteemiä.Yleisemmässä tapauksessa työkontribuutioita voi olla muitakinkuin tilavuudenmuutostyö, ja myös hiukkaslajeja voi olla useampia. Jos merkitsemmed¯W = YdX, on sisäisen energian luonnollisten muuttujien joukko{S, X, N i }, missä X voi sisältää useamman muuttujan. Seuraavassa oletamme,että systeemi on tilavuudenmuutostyötä tekevä yksinkertainen PTV-systeemi.Esitettävät tulokset ovat kuitenkin helposti yleistettävissä myös monista ainekomponenteistakoostuvia tai vaikkapa magneettista työtä tekeviä systeemejäkoskeviksi.Esimerkki 5.1Ideaalikaasun Gibbsin vapaa energia. Määritelmän mukaanG = U−TS+ PV. (5.29)Ideaalikaasun entropia yhtälöstä (4.57) on[ ( ) ]Tf /2VS = s 0 N+k B N lnT 0 v 0 N[ ( ) ]T( f+2)/2P= 0s 0 N+k B N ln,T 0 P

5.4. MIKSI TERMODYNAAMISIA POTENTIAALEJA KUTSUTAAN MYÖSVAPAIKSI ENERGIOIKSI? (6.1) 79missä jälkimmäisessä muodossa on käytetty ideaalikaasun tilanyhtälöä.Sijoittamalla entropian lauseke, ideaalikaasun sisäinenenergia (1.9) sekä tilanyhtälö yhtälöön (5.29) saadaan{ [ (G(T, P, N) = f ) ]}T( f+2)/22 k PBNT−T s 0 N+k B N ln0+ k B NTT 0= k B NT{f + 22[ (− s )0 T ( f+2)/2P− ln0k B T 0 PP]}.(5.30)Tulos on ideaalikaasun Gibbsin energia luonnollisten muuttujiensaavulla lausuttuna.Esimerkki 5.2Sekoitusentropia (6.6). Kappaleessa 4.8 tutkittiin kahden ideaalikaasunsekoittumista. Sama tarkastelu voidaan tehdä myös termodynamiikanyleistä formulaatiota käyttäen. Prosessi tapahtuuvakiolämpötilassa ja -paineessa, joten sopiva termodynaaminenpotentiaali kuvaamaan systeemiä on Gibbsin vapaa energia.Edellisen esimerkin nojalla ideaalikaasun Gibbsin energia voidaankirjoittaa muodossaG(T, P, N) = k B NT[φ(T)+ln P], (5.31)missä lämpötilasta riippuva funktio φ(T) sisältää myös kaikki vakiotermit.1 Ennen sekoittumistaG a = k B N 1 T[φ 1 (T)+ln P]+ k B N 2 T[φ 2 (T)+ln P].Huomaa, että funktio φ ei ole sama molemmille kaasuille. Sekoittumisenjälkeen kaasujen osapaineet ovat P 1 ja P 2 (P = P 1 + P 2 ) jaGibbsin energia onG n = k B N 1 T[φ 1 (T)+ln P 1 ]+k B N 2 T[φ 2 (T)+ln P 2 ].Näiden erotus G n − G a ≡ ∆G mix on sekoittumiseen liittyvä Gibbsinenergia:∆G mix = k B N 1 T ln P 1P + k BN 2 T ln P 2P= k B N 1 T ln x 1PP+ k BN 2 T ln x 2PP= k B N 1 T ln x 1 + k B N 2 T ln x 2 . (5.32)1 Huomaa, että yhtälö (5.31) on dimensionaalisesti kelvoton. Kyseinen muoto on valittu tähänvain matemaattisen yksinkertaisuuden vuoksi.

80 LUKU 5. TERMODYNAAMISET POTENTIAALIT ELI VAPAAT ENERGIATKoska S = −(∂G/∂T) P,N , sekoitusentropiaksi saadaan∆S mix = −k B N 1 ln x 1 − k B N 2 ln x 2= −k B N(x 1 ln x 1 + x 2 ln x 2 ), (5.33)missä N = N 1 + N 2 . Tulos on tietenkin sama kuin kappaleessa 4.8johdettu. Jos kyseessä olisi ollut reaalikaasu, ei sekoitusentropiaaolisi voinut laskea näin yksinkertaisesti, koska vuorovaikuttavillekaasuille Gibbsin vapaata energiaa ei voi lausua summana osakaasujenGibbsin energioista.5.4.1 Joulen ja Thomsonin ilmiö (3.7)Tarkastellaan lämpöeristetyn kaasun pakotettua virtausta huokoisen väliseinänläpi kuvan 5.4 mukaisessa systeemissä. Mäntien avulla paineet P 1 ja P 2 pidetäänprosessin aikana vakioina siten, että P 1 > P 2 koko ajan. Olkoon alkutilassaV 1 = V a , V 2 = 0 ja lopputilassa V 1 = 0, V 2 = V l . Vaikka prosessi onilmiselvästi irreversiibeli, on alku- ja lopputilat mahdollista yhdistää termodynaamisesti.Systeemin tekemä työ differentiaalisessa siirroksessa koostuu väliseinälläerotettujen systeemin osien tilavuudenmuutostöistä:Koska P 1 ja P 2 ovat vakioita,d¯W = P 1 dV 1 + P 2 dV 2 .∫ ∫ 0 ∫ Vl∆W = d¯W = P 1 dV 1 + P 2 dV 2 = P 2 V l − P 1 V a . (5.34)V a 0Lämpöeristyksen vuoksi ∆Q = 0, joten sisäisen energian muutos onJärjestelemällä termit havaitaan, että∆U = U l − U a = −∆W = P 1 V a − P 2 V l .U a + P 1 V a = U l + P 2 V l .Prosessissa U+PV eli entalpia säilyy siis vakiona:∆H = H l − H a = 0,ts. prosessi on isentalpinen.Tarkastellaan nyt reversiibeliä reittiä isentalpisessa muutoksessa. Hiukkasmääränpysyessä vakionadH = TdS+VdP = 0

5.4. MIKSI TERMODYNAAMISIA POTENTIAALEJA KUTSUTAAN MYÖSVAPAIKSI ENERGIOIKSI? (6.1) 81P 1 P 1 V 1 P 2 V 2 P 2T 1 T 2Kuva 5.4: Kaasun pakotettu virtaus huokoisen väliseinän läpi.eli(dS) H = − V T (dP) H. (5.35)Tutkitaan lämpötilan muutosta prosessissa lausumalla se entropian ja paineenmuutosten avulla ( ) ( )∂T ∂TdT = dS+ dP.∂S P ∂P SKun muistetaan, että C P = T(∂S/∂T) P ja käytetään Maxwellin relaatiota(∂T/∂P) p = (∂V/∂S) P , saadaan dT muotoondT = T C PdS+( ) ∂VdP.∂S PSeuraavaksi tarvitaan aputulosta (A.6), johon sijoitetaan w → T, y → S, x → Vja z → P. Saadaan( ) ( )∂V ∂T/ ( )∂T=.∂S P ∂S P ∂V PTämän avulladT = T C PdS+( ) ∂T∂S P( ) ∂VdP,∂T Pmissä on käytetty myös tulosta (A.4). Mutta (∂T/∂S) P = T/C P , ja kun huomioidaanyhtälö (5.35), saadaaneli( ) ∂T∂P HdT = T [( ) ∂V− V ]dPC P ∂T P T= T [( ) ∂VC P ∂T P− V ]= V (Tα P − 1), (5.36)T C Pmissä α P on kappaleessa 4.9 määritelty tilavuuden lämpölaajenemiskerroin jaon Joulen ja Thomsonin kerroin.( ) ∂T≡ µ JT (5.37)∂P H

82 LUKU 5. TERMODYNAAMISET POTENTIAALIT ELI VAPAAT ENERGIATTµ JT > 0, jäähtyy µ JT < 0, lämpeneeKuva 5.5: Joulen ja Thomsonin kerroin on positiivinen, kun isentalpien (harmaatkäyrät) kulmakertoimet ovat positiiviset. Isentalpien maksimikohtienkautta piirretty käyrä kertoo inversiolämpötilan.PKoska prosessissa entropia kasvaa, nähdään yhtälöstä (5.35), että paine aleneeeli dP on negatiivinen. Jos Tα P > 1, on yhtälön (5.36) perusteella µ JT > 0eli kaasu jäähtyy. Jos taas Tα P < 1, kaasu lämpenee, koska µ JT < 0. Kaasunlämpötilakäyttäytymiseen vaikuttaa työkontribuutio (5.34): Jos P 1 V a > P 2 V l ,kaasuun tehdään työtä ja se lämpenee. Jos taas P 1 V a < P 2 V l , kaasu tekee työtäja se jäähtyy.Joulen ja Thomsonin kertoimen merkinvaihdos tarkoittaa, että on olemassatietty ns. inversiolämpötila, jossa µ JT = 0. Usein kaasuilla on ylempi ja alempiinversiolämpötila (kuva 5.5). Ideaalikaasulle kuitenkin( ) ∂V= ∂ k B NT= k BN∂T P,N ∂T P P = V T ,joten ideaalikaasun Joulen ja Thomsonin kerroin on nolla. Huoneenlämmössäilmapainetta lähellä olevissa paineissa reaalikaasut, lukuunottamatta kvanttikaasujavety, helium ja neon, jäähtyvät Joulen ja Thomsonin ilmiöissä. Joulenja Thomsonin ilmiötä käytetään hyväksi jäähdytyskoneissa ja nesteyttimissä.Joulen ja Thomsonin kertoimen merkin vaihdoksen ymmärtämiseksi kirjoitetaanentalpia potentiaalienergian U pot , kineettisen energian U kin = f /2k B TNja PV termin summana, H = U pot + U kin + PV, ja tutkitaan kuvaa 5.6 Lennardinja Jonesin aineen paineesta, (kokonais) energiasta, vuorovaikutus- elipotentiaalienergiasta, PV-termistä sekä entalpiasta tilavuuden funktiona. Lennardinja Jonesin malliaineessa, joka kuvaa esimerkiksi jalokaasuja varsinhyvin, kahden atomien tai molekyylien vuorovaikutus energia molekyylien

5.4. MIKSI TERMODYNAAMISIA POTENTIAALEJA KUTSUTAAN MYÖSVAPAIKSI ENERGIOIKSI? (6.1) 83etäisyyden r funktiona onφ LJ (r) = 4ε LJ[ ( σLJr) 12− ( σLJr) 6], (5.38)missä σ LJ on molekyylin kokoa ja ε LJ molekyylien välisen vuorovaikutuksenvoimakkuutta kuvaava parametri. Kahden molekyylin vetovoima on voimakkaimmillaanmolekyylien ollessa etäisyydellä r = 2 1/6 σ LJ , φ LJ (2 1/6 σ LJ ) = −ε LJ .Kun etäisyys on pienempi kuin r = σ LJ , molekyylit hylkivät toisiaan, eli vuorovaikutusenergiaon positiivinen, ja se kasvaa tällöin jyrkästi etäisyyden pienentyessä.Paine alenee aina (katso yhtälö (6.5) ja luku 6.8.2) tilavuuden kasvaessa,jolloin molekyylien välimatkat kasvavat. Kun molekyylien väliset etäisyydetovat keskimäärin yli σ LJ , potentiaalienergia U pot kasvaa (näillä etäisyyksillämolekyylit vetävät toisiaan puoleensa, potentiaalienergia on negatiivista ja selähestyy nollaa kun tilavuus kasvaa), ja PV termi lähestyy ideaalikaasu tulostaNk B T tilavuuden kasvaessa. Jotta entalpia H = U pot + U kin + PV voisi pysyävakiona tilavuuden kasvaessa täytyy lämpötilaan verrannollisen kineettisenenergian ja PV-termin summan pienentyä, eli lämpötilan laskea. Toisaaltamolekyylien joutuessa lähelle toisiaan potentiaalienergia on positiivista (repulsio,hylkiminen), ja se kasvaa tilavuuden pienentyessä eli molekyylien pakkautuessalähemmäs toisiaan. Potentiaalienergiassa on jyrkkä nousu ylöspäin tilavuuttaσLJ 3 pienemmillä keskimääräisillä molekyylitilavuuksilla, joilloin molekyylitovat kiinni toisissaan ja aine on kiinteää, mutta paine nousee jyrkästijo tilavuutta 2σLJ 2 pienemmillä molekyylitilavuuksilla, missä potentiaalienergiavielä laskee tilavuuden pienentyessä. Tällöin molekyylien ’kovien ytimien’viemä tila on noin puolet tai enemmän käytettävissä olevasta kokonaistilavuudesta,eli molekyylit alkavat törmäillä toisiinsa usein. Paine kasvaa tilavuudenpienentyessä nopeammin kuin 1/V (vertaa Lennardin ja Jonesin aineen painekäyrääideaalikaasun painekäyrään, joka käyttäytyy kuten 1/V), eli PV termikasvaa tilavuuden pienentyessä, ja tämä kasvu voittaa potentiaalienergianlaskun välillä σLJ 3 < V/N < 2σ3 LJ . Niinpä näillä etäisyyksillä summa U pot+PVkasvaa tilavuuden pienentyessä, eli pienenenee tilavuuden kasvaessa, jotenentalpian vakiona pitämiseksi kineettisen energian eli lämpötilan on noustava.Suora yhteys Joulen ja Thomsonin kertoimen merkin ja kuvan 5.6 entalpiakäyränvälille saadaan osittaiderivaattaidentiteetistä (A.5) entalpialle, paineelleja lämpötilalle( ) ( )∂T ∂P∂P H ∂H Tjosta edelleen seuraa( ) ∂H( ) ∂T ∂Pµ JT = = −( )T∂P H ∂H∂TP( ) ∂H∂P= −( ) ∂H= −1,∂T PC PT= −( ) ( )∂H ∂(V/N)∂(V/N) T∂PT.C P

84 LUKU 5. TERMODYNAAMISET POTENTIAALIT ELI VAPAAT ENERGIAT6Lennard−Jones T=2.0 ε/k B54321ε, ε/σ 30-1PPid ∝ N/V-2-3-4PV/N(PV/N) idU/N(U/N) idU pot/N-5H/N(H/N) id-60 1 2 3 4 5 6 7 8 9 10V/N(σ 3 )Kuva 5.6: Paine (yksiköissä ε LJ /σLJ 3 ), PV-termi, kokonaisenergia U, vuorovaikutuksenpotentiaalienergia U pot ja entalpia (painetta lukuunottamatta permolekyyli ja yksiköissä ε LJ ) Lennardin ja Jonesin aineelle sekä ideaalikaasulle(ideaalikaasulle U pot = 0).Koska lämpökapasiteetti vakiopaineessa on aina positiivinen(, C) P > 0, ja tilavuuskasvaa aina paineen alentuessa vakiolämpötilassa ∂(V/N)∂P< 0 (katsoTluku 6.8.2),)on Joulen ja Thomsonin kertoimen merkki sama kuin derivaatan, joka puolestaan nähdään kuvan 5.6 entalpiakäyrän käytöksestä.(∂H∂(V/N)T5.5 Pisaran tarina, osa 2: vapaan energian muutospisaran muodostumisessaTutkitaan jälleen pisaran muodostumista höyryssä. Pisaran ja höyryn välisettasapainoehdot johdettiin jo kappaleessa 4.12 suoraan termodynamiikan toisenpääsäännön avulla. Lasketaan nyt miten vapaa energia muuttuu, kun höyryynmuodostuu pisara: alkutilanteessa (johon viittaa alaindeksi 0) on vain homogeenistahöyryä, lopputilanteessa pisara jota ympäröi höyry. Oletetaan, ettähöyryn paine ja koostumus ei muutu pisaran muodostumisen seurauksena.Systeemi on kytketty lämpökylpyyn, joten lämpötila pysyy koko ajan samanakuin kylvyn lämpötila T 0 .

5.5. PISARAN TARINA, OSA 2: VAPAAN ENERGIAN MUUTOS PISARANMUODOSTUMISESSA 85Homogeenisen höyryn tai nesteen energia voidaan lausua muodossaU = T 0 S− PV + ∑ µ i N i ,ja faasien välisen rajapinnan (pinta-ala A) energia muodossaU = T 0 S+ Aσ+∑ µ i N i .Alkutilanteessa on vain höyryn (k) energiaaU 0 = T 0 S 0 − P 0 V 0 + ∑ µ 0 i,k N0 i,k .Lopputilanteessa systeemin kokonaisenergia on summa höyryn, nesteen (n) jarajapinnan(p) energioistaU = T 0 (S k + S n + S p )−P k V k − P n V n + σA+ ∑ µ i,k N i,k + ∑ µ i,n N i,n + ∑ µ i,p N i,p= T 0 S tot − P k V k − P n V n + σA+ ∑ µ i,k N i,k + ∑ µ i,n N i,n + ∑ µ i,p N i,p ,missä S tot = S k + S n + S p . Tässä tapauksessa sopiva vapaa energia voidaanvalita ainakin kolmella eri tavalla. Oikea valinta riippuu siitä, mikä todellisessakoetilanteessa tai ajatuskokeessa pysyy vakiona.1. Pidetään ensin kaasufaasin (höyryn) kemiallinen potentiaali µ i,k = µ 0 i,kja systeemin kokonaistilavuus V 0 = V k + V n vakioina. Tämä edellyttää,että systeemiin lisätään hiukkasia, jos kemiallinen potentiaali pyrkii laskemaan,ja poistetaan, jos kemiallinen potentiaali pyrkii nousemaanSuuri potentiaali on tällöin sopiva termodynaaminen potentiaali, ja alkutilassase onΩ 0 = U 0 − T 0 S 0 − ∑ µ 0 i,k N0 i,k = −P 0V 0 = −P 0 (V n + V k ).Lopputilan suuri potentiaali onΩ = U−T 0 S tot − ∑ µ 0 i,k N i,tot = U−T 0 S tot − ∑ µ 0 i,k (N i,k+N i,n + N i,p )= −P k V k − P n V n + σA+∑(µ i,n − µ 0 i,k )N i,n+∑(µ i,p − µ 0 i,k )N i,p.Suuren potentiaalin muutos pisaran muodostumisessa on siten∆Ω =(P 0 − P n )V n +(P 0 − P k )V k + σA+ ∑(µ i,n − µ 0 i,k )N i,n+∑(µ i,p − µ 0 i,k )N i,p.Jos oletamme, että paitsi kaasun kemialliset potentiaalit µ i,k , myös kaasunkoostumus x i,k pysyy muuttumattomana myös kaasun paineen onpysyttävä vakiona Maxwellin relaation (5.13)( ∂V∂N i)T,P,N j̸=i=( ) ∂µ∂PT,N i

86 LUKU 5. TERMODYNAAMISET POTENTIAALIT ELI VAPAAT ENERGIATseurauksena. Tämä nähdään kun määritellään partiaalinen molekyylitilavuus( ) ∂Vv i ≡(5.39)∂N i T,P,N j̸=i(katso luku 7.1), josta saadaan0 = dµ i,k⏐⏐⏐⏐xi,k,T= v i,k dP k ⇒ dP k = 0 ⇒ P k = P 0 .On huomattava, että vaikka Maxwellin relaatiossa (5.13) on merkittyhiukkasmäärät N i vakioiksi, intensiivisenä ominaisuutena kemiallinenpotentiaali ei riipu hiukkasmäärän absoluuttisista arvoista, vaan niidensuhteista eli mooliosuuksista. Suuren potentiaalin muutokseksi tuleetällöin∆Ω = (P 0 − P n )V n + σA+∑(µ i,n − µ 0 i,k )N i,n+∑(µ i,p − µ 0 i,k )N i,p. (5.40)2. Pidetään sitten kaasun paine vakiona P k = P 0 , samoin eri hiukkastyyppienkokonaislukumäärät N i,tot = N i,n + N i,k + N i,p = N 0 i,k .Gibbsin vapaa energia on silloin sopiva termodynaaminen potentiaali.Alku - ja lopputiloissa Gibbsin vapaa energia onG 0 = U 0 − T 0 S 0 + P 0 V 0 = ∑ µ 0 i,k N0 i,k(5.41)G = U−T 0 S tot + P 0 V tot = U−T 0 S tot + P 0 (V k + V n ) (5.42)= (P 0 − P n )V n + σA+∑ µ i,k N i,k + ∑ µ i,n N i,n + ∑ µ i,p N i,p .Gibbsin vapaan energian muutos pisaran muodostuessa on∆G =(P 0 − P n )V n + σA+ ∑ µ i,k N i,k + ∑ µ i,n N i,n + ∑ µ i,p N i,p − ∑ µ 0 i,k N0 i,k .Oletetaan jälleen, että kaasun koostumus pysyy pisaran muodostuessavakiona, jolloin vakiopaineesta ja Maxwellin relaatiosta (5.13) seuraa,että kemiallinen potentiaali pysyy vakiona µ i,k = µ 0 i,k. Käyttämällä hiukkasmääriensäilymistäsaadaanN i,tot = N i,n + N i,k + N i,p = N 0 i,k∆G = (P 0 − P n )V n + σA+∑ µ 0 i,k (N i,k−N 0 i,k )+ ∑ µ i,n N i,n + ∑ µ i,p N i,p= (P 0 − P n )V n + σA+∑ µ 0 i,k (−N i,n−N i,p )+∑ µ i,n N i,n + ∑ µ i,p N i,p∆G = (P 0 − P n )V n + σA+∑(µ i,n − µ 0 i,k )N i,n+∑(µ i,p − µ 0 i,k )N i,p. (5.43)

5.5. PISARAN TARINA, OSA 2: VAPAAN ENERGIAN MUUTOS PISARANMUODOSTUMISESSA 873. Oletetaan nyt, että kokonaishiukkasmäärät N i,tot = N i,n + N i,k + N i,p =N 0 i,k ja systeemin kokonaistilavuus V tot = V k + V n eivät muutu.Helmholtzin vapaat energiat alku- ja lopputiloissa ovatF 0 =U 0 − T 0 S 0 = −P 0 (V n + V k )+∑ µ 0 i,k N0 i,kF =U−T 0 S tot = −P k V k − P n V n + σA+ ∑ µ i,n N i,n + ∑ µ i,k N i,k + ∑ µ i,p N i,p .Helmholtzin vapaan energian muutos on siis∆F =(P 0 − P n )V n +(P 0 − P k )V k + σA+ ∑(µ i,k − µ 0 i,k )N i,k+∑(µ i,n − µ 0 i,k )N i,n+ ∑(µ i,p − µ 0 i,k )N i,p.Olettaen ettei pisaran muodostus muuta kaasun painetta P 0 = P k ja koostumustamyös kemiallinen potentiaali pysyy vakiona µ i,k = µ 0 i,k, ja saadaan∆F = (P 0 − P n )V n + σA+∑(µ i,n − µ 0 i,k )N i,n+∑(µ i,p − µ 0 i,k )N i,p.Huomaa, että vain kaasu on yhteydessä kylpyihin, ja siksi vapaita energioitaei voi turvallisesti laskea nesteen (esim. Ω n ) kaasun (esim. Ω k ) ja pintafaasin(esim. Ω p ) vapaiden energioiden summana (Mitkä näistä antavat oikean tuloksen?Miksi?)Ω ̸= Ω n + Ω k + Ω pG ̸= G n + G k + G pF ̸= F n + F k + F pEnergia voidaan kuitenkin aina turvallisesti laskea systeemin eri osien energioidensummanaU = U n + U k + U p ,ja olemme johtaneet kaavamme tästä lähtökohdasta.Oletuksilla jotka teimme, suuren potentaalin, Gibbsin vapaan energian jaHelmholtzin vapaan energian muutokset pisaran muodostuessa ovat yhtä suuret∆Ω = ∆G = ∆F. Kaikki oletukset ovat oleellisesti samoja: pisara on pienija kaasutankki suuri, joten pisaran muodostuminen ei merkittävästä vaikutakaasun ominaisuuksiin. Tasapainoehdot, jotka jo löydettiin suoraan entropiandifferentiaalin nollakohdasta luvussa 4.12, voidaan nyt johtaa vapaiden energioidenmuutoksista etsimällä muutoksen ∆Ω, ∆G tai ∆F derivaatan nollakohtia.Käytännössä lämpötila T, kaasun paine P 0 ja kemiallinen potentiaali µ 0 i,kpidetään vakiona, ja derivaatat otetaan

88 LUKU 5. TERMODYNAAMISET POTENTIAALIT ELI VAPAAT ENERGIAT• tilavuuden V suhteen, vakioina tällöin N i,n ja N i,p• nesteen hiukkasmäärien N i,n suhteen, vakiona tällöin V, N j,n , j ̸= i ja N i,pkaikilla i,• pintafaasin hiukkasmäärien N i,p suhteen, vakiona tällöin V, N j,p , j ̸= i jaN i,n kaikilla i.Näistä saadaan seuraavat tutut tasapainoehdot, eli paineille LaplacenyhtälöP n − P 0 = 2σ r ,missä r on tasapainopisaran säde, ja kemiallisille potentiaaleille yhtäsuurusµ i,n = µ i,k = µ i,p .Lämpötilaa koskevaa tasapainoehtoa ei vapaiden energioiden muutosten derivaatoistasaada, koska lämpötila on jo lausekkeiden johdossa oletettu vakioksi,ja sillä seurauksella muotoa TS olevat termit ovat kumoutuneet näistälausekkeista. Jotta muodostumisen vapaiden energioiden ∆Ω, ∆G tai ∆F derivaattojennollakohdat antaisivat nämä yksinkertaiset ehdot paineille ja kemiallisillepotentiaaleille 2 , täytyy käyttää Gibbsin ja Duhemin yhtälöä (4.7.2)vakiolämpötilassa dT = 0 kaasun ja nesteen kohdallaV k dP k = ∑ N i,k dµ i,k ,V n dP n = ∑ N i,n dµ i,nja Gibbsin adsorptioisotermiä (4.41) pintafaasin kohdalla−Adσ = ∑ N i,p dµ i,p .2 Oikeastaan voisi ottaa lopputilojen vapaiden energioiden Ω, G tai F, derivaatat, mutta alkutilojenvapaat energiat ovat tehdyillä oletuksilla vakioita Ω 0 , G 0 , F 0 , joten d∆Ω = dΩ−dΩ 0 = dΩ,ja vastaavasti Gibbsin ja Helmholtzin vapaille energioille. Jatkossa huomataan, että vapaiden energioidenerotukset johtavat yksinkertaisempiin kaavoihin kuin lopputilojen vapaat energiat.

Luku 6Faasien ja faasimuutostentermodynamiikkaa6.1 JohdantoaVaikka olemmekin jo sivunneet faaseja ja niiden tasapainoa “Pisaran tarina”- esimerkeissämme, palaamme nyt aiheeseen perusteellisemmin. Jos systeemikoostuu yhdestä homogeenisesta aineesta, sen sanotaan koostuvan yhdestäfaasista eli aineen olomuodosta. Esimerkiksi vesi voi olla höyryä, nestettätai kiinteää (eli jäätä). Aineen olomuotoa karakterisoi jokin termodynaaminenmuuttuja, tyypillisesti tiheys tai kemiallinen koostumus. Esimerkiksi kaasufaasion paljon harvempi kuin nestefaasi. Myös kiinteällä ja nestemäisellä faasillaon erilainen tiheys, ja sen lisäksi niillä on myös erilainen mikroskooppinen rakenne.Tietyissä olosuhteissa tasapainosysteemi voi koostua kahdesta tai useammastakeskenään tasapainossa olevasta faasista, jotka itsessään ovat homogeenisia.Tällaisia systeemejä kutsutaan heterogeenisiksi. Esimerkiksi, kun paine on1 atm ja lämpötila 0 ◦ C, nestevesi ja jää voivat esiintyä samassa tasapainosysteemissä.Tilamuuttujat määräävät tasapainosysteemin tilan. Tilamuuttujien muutoksetvoivat aiheuttaa poikkeaman tasapainosta ja aineen siirtymisen faasistatoiseen eli faasitransition (olomuodonmuutoksen). Faasimuutos ei kuitenkaantapahdu välttämättä heti, vaan aine saattaa joutua hyvinkin pitkäaikaiseen metastabiiliintilaan, jossa faasimuutos on mahdollinen, mutta tapahtuu vasta, jossysteemin jonkin tilamuuttujan paikallinen fluktuaatio on riittävän suuri. Sensijaan, jos aine on epästabiili, pienikin häiriö saa aikaan faasimuutoksen. Tässäkappaleessa tarkastellaan faasien tasapainoa ja stabiilisuutta sekä faasitransitioihinliittyviä ilmiöitä yksinkertaisissa PTV-systeemeissä.

90 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAA6.2 FaasitasapainoKappaleessa 4.12 johdimme tasopinnan erottamille faaseille tasapainoehdoiksi(tässä merkitään faaseja yleisesti merkinnöillä 1 ja 2 kaasuun ja nesteeseenviittaavien k:n ja n:n sijaan)T (1) = T (2)P (1) = P (2) (6.1)µ (1) = µ (2) ,mikä takaa reunaehdoista riippuen, ettädS⏐ = 0,U,V,NidU⏐ = 0,S,V,NidH⏐ = 0,S,P,NidF⏐ = 0,T,V,NidG⏐ = 0,T,P,NidΩ⏐ = 0,T,V,µieli systeemi on tasapainossa.Yhtälöt (6.1) ovat PTV-systeemin tasapainoehdot. Huomaa, että systeeminjakaminen kahteen faasiin asettamalla systeemiin kuvitteellinen väliseinä (kuva4.15) on pelkkä apuneuvo tasapainoehtojen johtamiseksi. Tulokset ovat tokivoimassa systeemin koostuessa kahdesta (tai useammasta) todellisesta faasista,mutta silloin faasien on pystyttävä vaihtamaan vapaasti sekä mekaanistaenergiaa että lämpöenergiaa ja hiukkasia. Muussa tapauksessa tasapainoehtoihin(6.1) tulee muutoksia. Esimerkkejä tästä näimme kappaleessa 4.12 ja tulemmenäkemään kappaleessa 7.3.6.3 StabiilisuusEdellä lausutut tasapainoehdot takaavat, että olemme löytäneet relevantin termodynaamisenpotentiaalin differentiaalin nollakohdan, mutta eivät vielä sitä,

6.3. STABIILISUUS 91Kuva 6.1: Vakaa, indifferentti ja epävakaa tasapaino.onko kyseessä minimi (kuten pitäisi stabiilissa tasapainossa olla sisäisen energia,entalpian, Gibbsin vapaan energian, Helmholtzin vapaan energian ja suurenpotentiaalin kohdalla) vai maksimi (kuten pitäisi stabiilissa tasapainossaolla entropian kohdalla).Kuvassa 6.1 on erityyppisiä derivaatan nollakohtia. Jos vakaassa tasapainossaolevaa systeemiä poikkeutetaan hiukan tasapainoasemasta, se palaa takaisinalkuperäiseen tasapainotilaan kuopan pohjalle. Jos indifferentissä tasapainossaolevaa systeemiä poikkeutetaan, se jää uuteen tasapainotilaan. Josepävakaassa tasapainossa olevaa systeemiä poikkeutetaan tasapainotilasta, seajautuu yhä kauemmas alkuperäisestä tilasta , kunnes mahdollisesti löytää uudentasapainotilan. Jotta tasapaino olisi vakaa, meidän on varmistuttava siitä,että derivaatan nollakohta on oikeastaan minimi, eikä maksimi tai satulapistetyyppinen(oikeanpuoleisin kuvan 6.1 käyristä). Minimissä pieni poikkeamamihin suuntaan tahansa johtaa aika termodynaamisen potentiaalin kasvuun,eli minimissä pätee esimerkiksi (δU) S,V,N ≥ 0. Tästä seuraa oleellisesti tuttuvaatimus toisen derivaatan positiivisuudesta minimissä, kuten seuraavassanähdään.Tutkitaan ensin esimerkkinä tilannetta, jossa entropia, tilavuus ja hiukkasmääräovat vakioita, joten sisäinen energia on sopiva termodynaaminenpotentiaali. Kuvitellaan jälleen eristetty systeemi jaetuksi kahteen osaan. Oletetaan,että entropia fluktuoi määränδS (1) = −δS (2) (6.2)mutta tilavuuden tai hiukkasmäärän fluktuaatioita ei esiinny. huomaa että systeeminkokonaisentropia pysyy vakiona. Entropian muutoksesta aiheutuvasisäisen energian toisen kertaluvun fluktuaatio voidaan kirjoittaa osien 1 ja 2energiafluktuaatioiden summana, jotka puolestaan molemmat kehitetään Tay-

92 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAAlorin sarjaksi entropiafluktuaatioiden avulla, joten tasapainossa on pädettävä(δU) S,V,N = (δU) (1)V,N +(δU)(2) V,N( ) ∂U (1)= (δS (1) )+∂S V,N+ 1 ( ∂ 2 ) (1)U2 ∂S 2≥ 0.V,N( ) ∂U (2)∂S(δS (1) ) 2 + 1 2V,N(δS (2) )( ∂ 2 U∂S 2 ) (2)V,N(δS (2) ) 2 + ...Ensin todetaan, että ensimmäiset derivaatat ovat nollia tasapainotilassa.Lisäksi huomataan, että( ∂ 2 U∂S 2 )V,N= ∂∂S( ) ∂U=∂S V,N( ) ∂T= T∂S V,N C Vja käytetään ehtoa (6.2) sekä termisen tasapainon vaatimusta T (1) = T (2) , saadaan[ ](δU) S,V,N = 1 2 (δS(1) ) 2 1TC (1) + 1VC (2) ≥ 0. (6.3)VKoska systeemin jako kahteen osaan voidaan tehdä millä tavalla hyvänsä(tämä on saman tyyppinen ajatuskulku kuin ‘kaikkien suuntien järkeily’), onepäyhtälö (6.3) voimassa aina vain, kun T/C V ≥ 0 eliC V ≥ 0. (6.4)ja on vaikea kuvi-( )Tämä onkin järkeenkäypä vaatimus , koska C V = d¯QdTtella lämpötilan laskevan jos systeemiin virtaa lämpöä.V,NTarkastellaan seuraavaksi Helmholtzin vapaata energiaa F(T, V, N). Helmholtzinvapaa energia minimoituu systeemissä, jossa lämpötila, tilavuus jahiukkasmäärä ovat vakioita. Jaetaan tällainen systeemi kahteen osaan 1 ja 2siten, että osien tilavuudet ovat V (1) ja V (2) ja hiukkasmäärät N (1) ja N (2) . Oletetaan,että systeemissä 1 tapahtuu tilavuuden fluktuaatio δV (1) ja vastaavastisysteemissä 2 fluktuaatio δV (2) = −δV (1) , jolloin kokonaistilavuus säilyy vakiona.Oletetaan lisäksi, että hiukkasmäärän fluktuaatioita ei esiinny. 1Tasapainon vaatimusten mukaisesti1 Huomaa, että intensiivisiä ominaisuuksia, kuten lämpötilaa, ei voi jakaa samalla tavalla kuinekstensiivisiä ominaisuuksia.

6.4. FAASIDIAGRAMMI JA GIBBSIN FAASISÄÄNTÖ (8.2, 8.3, 8.4) 93(δF) T,V,N = (δF) (1)T,N +(δF)(2) T,N( ) ∂F (1)= (δV (1) )+∂V T,N+ 1 ( ∂ 2 ) (1)F2 ∂V 2≥ 0.∂V 2 )T,NT,N( ) ∂F (2)∂V(δV (1) ) 2 + 1 2T,N(δV (2) )( ∂ 2 F∂V 2 ) (2)Taas ensimmäiset derivaatat ovat nollia tasapainossa. Koska( ∂ 2 F= ∂ ( ) ( )∂F∂P= − = 1∂V ∂V∂V Vκ TT,NT,NT,N(δV (2) ) 2 + ...ja koska tässäkin systeemin jako on mielivaltainen, on isotermisen kokoonpuristuvuudenoltava positiivinen:κ T ≥ 0. (6.5)Tämäkin tulos on(maalaisjärjen)mukainen, sillä kokoonpuristuvuus on∂Pmääritelty κ T ≡ −V1 , ja paineen kasvaessa tilavuuden täytyy kaiken∂V T,Njärjen mukaan pienentyä.Lisää stabiilisuusehtoja voidaan johtaa tarkastelemalla muiden ekstensiivistensuureiden fluktuaatioita ja muita termodynaamisia potentiaaleja. Jos termodynaaminenpotentiaali ondΦ =r∑i=1I i dX i −n∑j=r+1X j dI j , (6.6)missä X i :t ovat ekstensiivisiä ja I j :t intensiivisiä muuttujia, ovat stabiilisuusehdotlausuttavissa muodossa( ) ∂Ii0 ≤. (6.7)∂X i X 1 ,...,X i−1 ,X i+1 ,...X r ,I r+1 ,...,I n6.4 Faasidiagrammija Gibbsin faasisääntö (8.2, 8.3,8.4)Tarkastellaan aluksi kahta saman aineen tasapainossa olevaa faasia A ja B. Tasapainoehtojen(6.1) mukaanT A = T BP A = P Bµ A = µ B .

94 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAAP1kiinteä2nesteCµ 1 = µ 2µ 2 = µ 33µ 1 = µ 3 tkaasuKuva 6.2: Yksinkertaisen PTV-systeemin faasidiagrammi (P, T)-tasossa.TVoidaan siis lausuaµ A (P, T) = µ B (P, T), (6.8)missä P ja T ovat tasapainoehtojen mukaiset paine ja lämpötila. Tasapainotilojakuvaavat yhtälön (6.8) ratkaisut(P, T)-tasossa eli tasapainokäyrät, ja kuvaajaakutsutaan faasidiagrammiksi eli faasikuvaajaksi. Esimerkki faasidiagrammista onesitetty kuvassa 6.2. Tasapainossa olevat faasiparit AB ovat faasit 1-2 (kiinteäneste),2-3 (neste-kaasu) ja 1-3 (kiinteä-kaasu). Nestefaasin tai kiinteän faasinkanssa tasapainossa olevaa höyryä kutsutaan kylläiseksi tai saturoituneeksi. Yhdessä(ja vain yhdessä) pistessä t kaikki kolme faasia (kaasu-neste-kiinteä) ovatkeskenään tasapainossa. Tämä piste on kolmoispiste, ja siinä on voimassaµ 1 (P t , T t ) = µ 2 (P t , T t ) = µ 3 (P t , T t ).Kaasun ja nesteen tasapaino on mahdollinen vain lämpötiloissa, jotka ovatkriittisen pisteen C alapuolella.Kuvan 6.2 tapauksessa neste jäätyy, kun paine kasvaa riittävästi. Näinkäykin useimmille aineille, mutta vesi sen sijaan sulaa paineen kasvaessa. Kuvan6.2 koordinaatistossa nesteen ja kiinteän faasin tasapainokäyrä vedelle kallistuisihieman vasemmalle. Sulamispiste /jäätymispiste on lämpötila, jossa vallitsevassapaineessa neste ja kiinteä faasi ovat tasapainossa. Ilmakehän olosuhteissanesteen ja kiinteän aineen paine on ilmakehän kokonaispaine.Faasidiagrammin paine kaasun osalta on kyseisen aineen osapaine, ei kaasufaasinkokonaispaine. Kaasu-neste tasapainokäyrä kertoo tasapainohöyrynpaineen lämpötilan funktiona. Jos suljettuun säiliö täytetään osittain nesteellä,nesteestä haihtuu molekyylejä muodostaen kaasufaasin. Kaasufaasin molekyyleilläon tietty todennäköisyys osua nestepintaan ja muuttua osaksi nestettä,eli tiivistyä. Kun nämä kaksi prosessia ovat dynaamisessa tasapainossa(eli yksittäisiä molekyylejä siirtyy koko ajan molempiin suuntiin, mutta nettovuoon nolla), nesteestä lähtee aikayksikössä yhtä paljon molekyylejä kuin sinnepalaa, ja nesteen molekyylien osapaine kaasufaasissa on tasapainohöyryn

6.4. FAASIDIAGRAMMI JA GIBBSIN FAASISÄÄNTÖ (8.2, 8.3, 8.4) 95paine tai kylläisen höyryn paine tai saturaatiohöyrynpaine. Kun lämpötila onkorkeampi, nesteen pinnalta karkaaminen on helpompaa molekyylien suuremmankineettisen energian ansiosta. Haihtuminen on nesteen pinnalla tapahtuvailmiö, kun taas kiehumisessa kaasua syntyy nesteen sisällä. Jos on olemassanestepinta, sen yläpuolella höyry pyrkii asettumaan tasapainohöyrynpaineeseen: jos höyryn paine on alempi, nestettä haihtuu (enemmän kuin kaasuatiivistyy), kunnes saavutetaan kylläinen höyrynpaine tai neste loppuu.Jos taas höyryn paine on korkeampi, kaasua tiivistyy (enemmän kuin nestettähaihtuu), kunnes ollaan päästy tasapainotilanteeseen.Kaasufaasin kokonaispaine ja tutkittavan aineen osapaine ovat yhteydessäkiehumispisteen määritelmän kautta: Nesteen kiehumispiste on lämpötila, jossatasapainossa olevien kaasun ja nesteen paine eli tasapainohöyrynpaine onyhtä suuri kuin ulkoinen kokonaispaine, eli arkioloissa ilmanpaine. Kuumassavedessä muodostuu vesihöyrykuplia, joiden paine on tasapainohöyrynpaine.Jos tämä paine on alempi kuin ilmanpaine, kuplat eivät pääse kasvamaan ,koska niitä puristaa kokoon paine joka on ilmapaine lisättynä hydrostaattisellapaineella (joka riippuu siitä kuinka syvällä veden pinnan alapuolella ollaan).Kiehumispisteessä kuplan paine on yhtä suuri kuin ulkoinen paine, jakuplat pääsevät kasvamaan ja nousemaan nesteen pintaa kohti. Kuvan 6.2 faasidiagrammissakiehumispiste löydetään valitsemalla P-akselilta ulkoinen paine,esimerkiksi 1atm, piirtämällä sitä vastaava vaakasuora viiva, ja etsimällälämpötila, jossa kaasu-neste tasapainokäyrä kolmoispisteen t ja kriittisen pisteenC välillä leikkaa tämän vakiopaineviivan. Kun kokonaispaine kasvaa, kiehumislämpötilakinnousee. Tähän perustuu painekattilan käyttö ruuanlaitossa.Ruoka kypsennetään korkeassa paineessa, jolloin päästään korkeampaanlämpötilaan kuin 100 °C, ja kypsyminen on nopeampaa. Hiljaa tai rajusti kiehuvavesi ovat nimittäin molemmat normaalissa ilmanpaineessa lämpötilassa100 °C. Vuoristossa, missä ilmanpaine on alempi, ruuan kypsyminen avonaisessakattilassa puolestaan on hitaampaa kuin meren pinnan tasolla, koska kiehumispisteon alempi, ja neste ei pääse lämpenemään sen yläpuolelle.Faasidiagrammi voidaan esittää myös (v, T)-tasossa (v = V/N) tai (ρ, T)-tasossa, kuten kuvassa 6.3. Huomataan, että tiheydessä on hyppäys tasapainossaolevien faasien välillä. Kriittisessä pisteessä tiheysero kutistuu nollaan,ja sen yläpuolella ei ole enää erillisiä kaasu- ja nestefaaseja.Kuvien 6.2 ja 6.3 tapauksessa on vain yksi ainekomponentti ja tasapainossaolevia faaseja on enintään kolme. Kuinka monta faasia voi olla yhtä aikaatasapainossa keskenään, jos systeemissä on r ainekomponenttia?Oletetaan PTV-systeemi, jossa komponenttien j = 1, . . . , n mooliosuudetfaasissa p ovat x j,p . Tasapainossa olevien faasien määrä olkoon p max . Koskamooliosuuksille päteenx j,p = 1∑j=1kaikissa faaseissa p = 1, . . . , p max , on riippumattomia mooliosuuksia n − 1kappaletta. Kun otetaan huomioon muuttujat P ja T, on riippumattomia muuttujiakaikkiaan p max (n−1)+2 kappaletta.

96 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAATasapainossa faasien kemialliset potentiaalit ovat samat kullekin molekyylilajille:µ 1,1 = µ 1,2 = ··· = µ 1,pmaxµ 2,1 = µ 2,2 = ··· = µ 2,pmax. . .µ n,1 = µ n,2 = ··· = µ n,pmax .Laskemisen helpottamiseksi valitaan vaikkapa faasi 1 vertailufaasiksi, jonkakanssa kaikilla muilla faaseilla tulee olla samat kemialliset potentiaalit.Ylläolevat ehdot toteutuvat jos ja vain jos kaikille komponenteille j (joita onn kappaletta) päteeµ j,p=2 = µ j,p=1µ j,p=3 = µ j,p=1. . .µ j,p=pmax = µ j,p=1 . (6.9)Tämä antaa n(p max − 1) sidosehtoa. Jotta yhtälöryhmällä (6.9) olisi ratkaisuolemassa, pitää riippumattomia muuttujia olla vähintään yhtä paljon kuin sidosehtoja:p max (n−1)+2 ≥ n(p max − 1)elip max ≤ n+2. (6.10)Yhtälö (6.10) on Gibbsin faasisääntö.Esimerkiksi puhtaalle (eli yhden komponentin) aineelle n = 1 ja p max ≤1+2 = 3, kuten pitääkin. Puhtailla aineilla on aina vain yksi kaasumainen faasija tavallisesti vain yksi nestemäinen faasi, mutta kiinteässä olomuodossa voiTkaasuCnestekiinteäT tρKuva 6.3: Faasidiagrammi(ρ, T)-tasossa. Lämpötilassa T t aineella on kolmoispiste.C on kriittinen piste.

6.5. FAASIMUUTOKSEN KERTALUKU 97esiintyä useita eri faaseja. Näin on esimerkiksi vedelle. Useammasta nestefaasistaon esimerkkinä helium jolla on sekä tavallinen nestefaasi että supranestefaasi.Gibbsin faasisääntö pätee myös kaikenlaisille faaseille eli esimerkiksikorkeintaan kolme kiinteää faasia voi olla tasapainossa keskenään.6.5 Faasimuutoksen kertalukuKuva 6.4: Gibbsin vapaa energia lämpötilan ja paineen funktiona ja senlämpötila- ja painederivaattojen käyttäytyminen ensimmäisen kertaluvun faasitransitiossa.Kuviin on merkitty ’neste’ ja ’kaasu’ faasien nimiksi havainnollisuudenvuoksi, mutta yhtä hyvin ’neste’ voi olla mikä tahansa alemmassalämpötilassa valitseva faasi ja ’kaasu’ edelliseen verrattuna korkeammassalämpötilassa vallitseva faasi. Huomaa, että oikeanpuoleiset kuvat eivät olesikäli yleispäteviä, että esimerkiksi vedelle kiinteä (alemman lämpötilan faasi)→ neste (ylemmän lämpötilan faasi) faasimuutoksessa tilavuus laskee, eikasva, kuten kuvissa. Entropia sen sijaan kasvaa aina kun siirrytään alemmanlämpötilan faasista ylemmän lämpötilan faasiin.Faasimuutokset jaetaan ensimmäisen ja toisen kertaluvun transitioihin.Jaottelun perusteena ovat Gibbsin vapaan energian derivaatat. Tasapainoehtojenmukaisesti faasimuutoksessa paine, lämpötila ja kemiallinen potentiaaliovat vakioita. Koska µ = (∂G/∂N) P,T on tämä Gibbsin funktion derivaattaaina jatkuva ylitettäessä tasapainokäyrä. Sen sijaan k:n derivaatat paineen jalämpötilan suhteen voivat olla epäjatkuvia.

98 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAAEnsimmäisen kertaluvun transitiossa derivaatat( ) ( )∂G∂GV =ja S = −∂P∂TT,Novat epäjatkuvia. Gibbsin vapaan energian ja sen derivaattojen käyttäytyminenlämpötilan funktiona 1. kertaluvun muutoksessa on esitetty kuvassa 6.4. Toisenkertaluvun eli jatkuvassa transitiossa epäjatkuvuus esiintyy vasta toisissa derivaatoissa.( ∂ 2 G∂P 2 )T,N=( ) ∂V∂P T,N,( ∂ 2 G∂T 2 )P,NP,N= −( ) ∂S∂T P,N( ∂ 2 )G=∂P∂T( ) ∂V= −∂T P,N( ) ∂S∂P T,N,( ∂ 2 G∂N 2 )T,P=( ) ∂µ∂N T,Pja( ∂ 2 )G=∂P∂N( ) ∂V=∂N T,P( ) ∂µ∂P T,NTaulukossa 6.1 vertaillaan ensimmäisen ja toisen kertaluvun faasitransitioidenpiirteitä Kaikki “arkipäivän” faasimuutokset ovat ensimmäistä kertalukua. Tavallisinesimerkki toisen kertaluvun muutoksesta on paramagneettisen ja ferromagneettisenfaasin välinen transitio.Taulukko 6.1: Ensimmäisen ja toisen kertaluvun faasitransitioiden vertailu.Ensimmäisen kertaluvun transitio: Toisen kertaluvun transitio:Jotkut G:n derivaatat epäjatkuviaFaasitransitio alkaa nukleaatiollaMuutokseen liittyy latentti lämpöEpäjatkuvia G:n toisia derivaattojaKaikki G:n derivaatat jatkuviaEi nukleaatiotaEi latenttia lämpöäEpäjatkuvia G:n toisia derivaattojaEnsimmäisen kertaluvun faasitransitioon liittyy faasimuutoslämpö eli latenttilämpö:∆Q = T∆S = ∆U+P∆V = ∆(U+PV) = ∆H, (6.11)missä toiseksi viimeinen yhtäsuuruus seuraa paineen vakioisuudesta muutoksessa.Kyseessä on siis entalpian muutos.

6.6. VAPAA ENERGIA-DIAGRAMMIT (8.1) 99Kuva 6.5: Gibbsin vapaa energia lämpötilan funktiona ja senlämpötiladerivaatan käyttäytyminen toisen kertaluvun faasitransitiossa.6.6 Vapaa energia-diagrammit (8.1)Seuraavaksi tarkastellaan, miten ensimmäisen kertaluvun faasimuutos näkyyvapaan energian käyttäytymisessä. Käytetään esimerkkinä Gibbsin vapaataenergiaa k, joka kuten muutkin termodynaamiset potentiaalit, on systeeminsisäisten järjestysparametrien funktio. Tässä tarkastelemme yksinkertaista tapausta,jossa järjestysparametrina toimii molekyylien tiheys ρ = N/V. Tässätarkastelussa ajatellaan koko systeemissä olevan sama tiheys, eli aine on kokonaanjoko nesteenä tai kaasuna, eli neste-kaasu rajapintaa ei systeemissä oleollenkaan.Kuva 6.6 esittää Gibbsin vapaata energiaa tiheyden funktiona erilämpötiloissa T.Kuva 6.6: Gibbsin vapaa energia molekyylitiheyden funktiona erilämpötiloissa T.

100 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAATasapainotila annetuilla ulkoisilla parametreillä (Gibbsin energian tapauksessatietty paine ja lämpötila sekä vakiohiukkasmäärä) löytyy vapaan energian minimistä.Minimejä löytyy kuitenkin kuvan kaikissa lämpötiloissa kaksi: alemmantiheyden minimi vastaa kaasua (k), ylemmän tiheyden minimi nestettä(n). Saman paineen voi siis samassa lämpötilassa aikaansaada joko harva kaasutai tiheä neste. Minimeistä alempi on vakaa eli stabiili faasi, mutta toinenkinminimi eli metastabiili faasi on olemassa. Ajatellaan systeemiä, joka onnesteenä eli oikeanpuoleisessa minimissä faasiotransitiolämpötilaa alemmassalämpötilassa (ylin käyrä kuvassa 6.6 ) Kun lämpötila nousee (paineen pysyessävakiona) minimien suhteellinen korkeus muuttuu, ja transitiolämpötilassa neovat yhtä korkealla. Lämpötilan noustua transitiolämpötilan yläpuolelle kaasuavastaava minimi onkin alempana. Systeemi pysyy kuitenkin edelleen nesteenä,koska se ei “näe” välissä olevan kukkulan taakse, ja jää loukkuunylempään minimiin.Kuvassa 6.7 on piirretty minimien korkeudet lämpötilan funktiona. Tämävastaa luvun 5.3 tasapainoarvon G eq käytöksen tutkimista. Periaatteessa, elijos systeemi kykenisi hakeutumaan globaaliin minimiin, se seuraisi kokoajan lämpötilan muuttuessa kuvan mustaa käyrää. Valli minimien välissä saakuitenkin systeemin jatkamaan katkoviivalla merkityllä käyrällä lämpötilanmuuttuessa transitioarvon yli, kunnes sitä häiritään tai sen sisäiset fluktuaatiotriittävän pitkän odottelun jälkeen saavat sen löytämään alemman minimin.Tätä uuden, energeettisesti edullisemman eli vakaan faasin muodostumistametastabiilissa faasissa kutsutaan nukleaatioksi. Prosessi, jolla se tapahtuu,on aidosti dynaaminen, ja siksi tasapainotermodynamiikan kuvailualueenulkopuolella. Esimerkiksi neste-kaasu transitiossa kyse on molekyyliryppäidenmuodostumisesta molekyylien törmäilyjen seurauksena. Toisaaltaryppäät hajoavat jos niiden sidosnergia ei ole riittävän suuri, ja nukleaation (elifaasimuutoksen alkamisen) nopeus määräytyy hajoamis- ja törmäilyprosessienkilpailusta.Kuva 6.7: Gibbsin vapaan energian nestettä (n) ja kaasua (k) vastaavien tasapainoarvojenkehitys lämpötilan (vasen kuva) ja paineen (oikean puoleinen kuva)muuttuessa.Kuva 6.8 esittää Gibbsin vapaan energian käyttäytymistä toisen kertaluvunfaasitransitiossa. Tässä esimerkkinä on transitio paramagneettisesta fer-

6.7. CLAUSIUKSEN JA CLAPEYRONIN YHTÄLÖ (8.5, 8.6) 101romagneettiseen faasiin lämpötilan laskiessa. Korkeammassa lämpötilassa onvain yksi minimi nollamagnetoitumassa, joka transitiolämpötilasssa jakautuukahdeksi minimiksi. Tässä tapauksessa systeemi ei voi jäädä loukkuun“vanhaan” korkeamman energian minimiin nollamagnetoitumaan. Alhaisessalämpötilassa molemmat minimit ovat samalla korkeudella, vastaten magnetoitumaaesimerkiksi ylös ja alas, ja ovat molemmat vakaita tiloja.Kuva 6.8: Gibbsin vapaa energia järjestysparametrina toimivan magnetoitumanfunktiona toisen kertaluvun para-ferromagneettisessa faasitransitiossa.6.7 Clausiuksen ja Clapeyronin yhtälö (8.5, 8.6)Tasapainoehdoista voidaan johtaa lauseke tasapainokäyrän tangentille. Oletetaankaksi faasia, 1 ja 2, joita erottaa faasikäyrä (kuva 6.9). Tasapainoehtojenmukaisesti faasikäyrälläµ 1 (P, T) = µ 2 (P, T).Koska G = µN, on myösG 1 (T, P, N) = G 2 (T, P, N). (6.12)Kokonaisainemäärän pysyessä vakiona Gibbsin vapaan energian muutos ondG = −SdT+ VdP. Kuljetaan tasapainokäyrää pisteestä(P, T) pisteeseen(P+dP, T+dT) kuvan 6.9 mukaisia reittejä pitkin. Toinen reiteistä on siis kokonaanfaasissa 1 ja toinen faasissa 2. Vastaavat Gibbsin energian muutokset ovatdG 1 = −S 1 dT+ V 1 dPdG 2 = −S 2 dT+ V 2 dP.

102 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAAKuva 6.9: Faaseja 1 ja 2 erottava tasapainokäyrä, Gibbsin vapaan energianmuutokset faaseissa 1 ja 2, sekä faasimuutoksessa tapahtuva tilavuuden muutosja entalpian muutos.Mutta koska molemmissa tapauksissa päädytään samaan pisteeseen ja muutoson reversiibeli, on dG 1 = dG 2 eli−S 1 dT+ V 1 dP = −S 2 dT+V 2 dP,josta saadaan( ) dP= S 2 − S 1= ∆SdT koeks V 2 − V 1 ∆V ,missä “koeks” tarkoittaa koeksistenssia eli tasapainotilaa. Entalpian differentiaaliondH = VdP+TdS+∑ µ i dN i . (6.13)iKun faaseja erottaa tasopinta ja vakioainemäärä siirtyy tasapainossa faasistatoiseen, pysyvät siis paine ja lämpötila vakioina, jolloin dH faasien välillä =TdS faasien välillä . Entropian muutos siirryttäessä faasista toiseen voidaanlausua entalpian muutoksen eli latentin lämmön avulla, ∆S faasien välillä =∆Q faasien välillä /T = ∆H faasien välillä /T, ja näin saadaan Clausiuksen ja Clapeyroninyhtälö( ) dPdT∆H faasien välillä∆V faasien välillä. (6.14)= 1koeks THuomaa, että Clausiuksen ja Clapeyronin yhtälö pätee vain faaseja rajoittavallatasapainokäyrällä. Tasapaino voi olla minkä tahansa PTV-systeemissä

6.7. CLAUSIUKSEN JA CLAPEYRONIN YHTÄLÖ (8.5, 8.6) 103esiintyvien faasien välillä, jolloin tietysti ∆H on kyseiseen transitioon liittyvälatentti lämpö. Esimerkiksi:TransitioLatentti lämpökorkeampi T alempi Tkaasu ↔ neste höyrystymislämpöneste ↔ kiinteä sulamislämpökaasu ↔ kiinteä sublimoitumislämpöLatentti lämpö ∆H on positiivinen siirryttäessä alemman lämpötilan faasista(esim. vesijää) korkeamman lämpötilan faasiin (esim. nestevesi).Tämän voi päätellä kuvien 6.6 ja 6.7 käyrien käytöksestä: olkoon T 1 T trans , jolloin puolestaankaasu on vakaa faasi ja Gk 2 < G2 n . Tästä seuraa, että siirryttäessä lämpötilastaT 1 lämpötilaan T 2 täytyy Gibbsin vapaan energian muutoksen kaasussa ollasuurempi kuin nesteessä (katso kuvaa 6.6: ero ylimmän ja alimman käyränvälillä kaasua vastaavan minimin korkeudessa täytyy olla suurempi kuin nestettävastaavan minimin korkeudessa, jotta kaasua vastaava minimi muuttuisialimmaksi minimiksi)G 1 n − G 2 n < G 1 k − G2 k .Merkitään ∆T = T 2 − T 1 > 0, jolloin saadaanja edelleenG 1 n − G 2 n∆T− G2 n − G 1 n∆T< G1 k − G2 k,∆T< − G2 k − G1 k.∆TKun lämpötilaero viedään infinitesimaalisen pieneksi saadaan( ) ( )∂Gn∂Gk− < −∂T∂TP,N.P,NKoska entropia voidaan lausua Gibbsin vapaan energian derivaattanalämpötilan suhteen( ) ∂GS = − ,∂T P,Non siis S n < S k ja ∆S ∆T>0 = S k − S n > 0. Entalpian differentiaalista (6.13)nähdään, että ∆S = 1/T∆H, joten koska T on positiivinen luku, ∆H ∆T>0 > 0.Tämä merkitsee, että esimerkiksi siirryttäessä nesteestä kaasuun eli haihtumistapahtumassanesteen molekyylit vaativat energiaa. Tämän voi tuntea uimisenjälkeen iholla: vaikka vesi ja ympäröivä ilma olisi lämmintä, tuntuu märkänälaiturilla seisominen kylmältä, kun vesimolekyylit riistävät haihtumiseen tarvitsemansaenergian ihosta. Tällä periaatteella toimivat myös jotkut veden tai

104 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAAviinin viilentämiseen tarkoitetut huokoiset saviastiat, jotka upotetaan veteenjotta ne kyllästyisivät vedellä: Kun tämä vesi haihtuu astian pinnalta, se viileneejopa 15 °C ympäristöä alempaan lämpötilaan. Saunojan iho on viilein pintasaunan yläosassa. Kuumalla kiukaalla höyrystynyt vesi tekee saunan ilmanylikylläiseksi veden suhteen ihmisen ihon lämpötilassa, ja vesi tiivistyy tämänvuoksi ihon pinnalle luovuttaen latentin lämpönsä, joka saa olon tuntumaankuumalta.Yleensä myös tilavuuden muutos ∆V on positiviinen siirryttäessä alemmanlämpötilan faasista korkeamman lämpötilan faasiin, mutta nestejäästä nesteveteensiirryttäessä tilavuus pienenee. Tämä johtaa veden kohdalla kiinteä-nestetasapainokäyrän kallistumiseen vasemmalle kuvan 6.2 faasidiagrammissa.Edellä latentti lämpö ∆H on faasimuutokseen liittyvä lämpö tietylle ainemäärälle.Taulukoissa latentit lämmöt ilmoitetaan ominaissuureina ∆h =∆H/massayksikkö, jolloin ∆h:n yksikkönä on kJ/kg tms.6.7.1 Kylläisen höyryn paineen lämpötilariippuvuusClausiuksen ja Clapeyronin yhtälöstä voidaan johtaa lauseke kylläisen höyrynpaineelle eli sen höyryn paineelle, joka on tasapainossa vastaavan nesteenkanssa annetussa faasitasapainokäyrän pisteessä (P, T).Olkoon nyt ∆h höyrystymislämpö moolia kohden. Clausiuksen ja Clapeyroninyhtälöstä saadaan( dPdT)koeks= 1 T∆H∆V = 1 ∆hT ∆v = 1 ∆h, (6.15)T v k − v nmissä v = V/n on moolitilavuus. Koska kaasun moolitilavuus v k on paljonsuurempi kuin veden moolitilavuus v n , voidaan v n approksimoida nollaksiyhtälössä (6.15). Koska ideaalikaasulaista v k = RT/P, saadaan( dPdT)koeks= 1 T∆hRT/P = ∆hRT 2 P.Jaetaan lämpötila- ja painetermit eri yhtälön eri puolille ja integroidaan jossainlämpötilassa T 1 tunnetusta kylläisen höyryn paineesta P sat (T 1 ) kylläisenhöyryn paineeseen P sat (T 2 ) lämpötilassa T 2 :∫ Psat (T 1 )P sat (T 2 )dPP = ∫ T2T 1∫∆h ∆h T2dTdT =RT2 R T 1T 2 ,missä on oletettu, että latentti lämpö ei riipu lämpötilasta. Integroinnin tuloksenasaadaanln P sat(T 2 )P sat (T 1 ) = ∆h ( 1− 1 ),R T 1 T 2josta kylläisen höyryn paine voidaan ratkaista:[ ( ∆h 1P sat (T 2 ) = P sat (T 1 ) exp − 1 )]R T 1 T 2(6.16)

6.8. FAASIMUUTOKSET JA VAN DER WAALSIN TILANYHTÄLÖ (7.2, 7.3)105eli(P sat (T) = vakio×exp− ∆hRT). (6.17)Tarkempi lauseke saadaan, jos tiedetään latentin lämmön lämpötilariippuvuus,esimerkiksi ∆h(T) = a+bT, missä a ja b ovat vakioita. 2Kylläisen höyrynpaineen lämpötilariippuvuuden voi havaita monissa arkipäiväntapahtumissa. Pyykki kuivuu paremmin korkeassa lämpötilassa,jossa tasapainohöyryn paine on korkea. Tietysti lisäksi tarvitaan hyvä tuuletus,jotta höyryn todellinen paine pyykin lähellä eli lähesty kylläistähöyrynpainetta. Pakastimeen muodostuu jäätä, jos ovea pidetään liiaksi auki,koska huoneenlämpöisen ilman sisältämä vesihöyry onkin ylikylläistä kun sejoutuu pakastimen kylmään lämpötilaan jossa kylläinen höyrynpaine on paljonalempi. Tällöin vesi pyrkii tiivistymään ja itse asiassa härmistyy jääksi.Keuhkoissa ruumiinlämpöiseksi ja vedellä kyllästyneeksi tullut ilma onkinviileään ulkoilmaan puhallettaessa ylikylläinen vesihöyryn suhteen, ja ilmanpölyhiukkasten ympärille muodostuu vesipisaroita, jotka näemme sumuna.Silmälasin linssin pinnalle tiivistyminen on helpompaa, joten ilmiön näkeehuoneenlämpötilassakin. On tärkeää muistaa, että kylläinen höyrynpaineon nesteen ominaisuus: nesteen koostumus ja lämpötila määräävät tasapainohöyrynpaineen.Esimerkiksi saunassa veden tiivistyessä iholle ihonlämpötila (eikä saunan ilman lämpötila) määrää kuinka ylikylläistä vesihöyryon ihon pinnalle tiivistyvän vesikalvon suhteen. Suhteellinen kosteuskertoo prosenteissa veden todellisen osapaineen verrattuna kylläiseenhöyrynpaineeseen. 100 % suhteellisessa kosteudessa vesihöyry on kylläistä.6.8 Faasimuutokset ja van der Waalsin tilanyhtälö(7.2, 7.3)6.8.1 Van der Waalsin tilanyhtälöIdeaalikaasun tilanyhtälön mukaan P ∝ ρ (ρ = N/V). Ideaalikaasussa ei sitenvoi esiintyä olomuodonmuutoksia, koska ei ole mahdollista löytää kahta tiheyttä,jotka vastaisivat samaa lämpötilaa, painetta ja kemiallista potentiaalia.Yksinkertainen ja havainnollinen tapa esitellä faasimuutosten teoriaa on kuvataainetta van der Waalsin tilanyhtälöllä (1.14). Se on muodoltaan kolmannenasteen polynomi, eli sopivilla parametrien a ja b arvoilla yhtälöllä on looppirakenne.Silloin tietyssä osassa(ρ, P)-tasoa yhtälöllä P vdW (ρ) = vakio on kaksiratkaisua (itse asiassa kolme, mutta yksi niistä on suljettava pois termodynaamisinperustein, kuten pian nähdään). Seuraavissa luvuissa selviää, millä ehdoillaratkaisut ovat olemassa ja mikä niistä vastaa aiemmin esitettyjä tasapainovaatimuksia.Ensin kuitenkin esitämme heuristisen johdon van der Waalsintilanyhtälölle.2 Jos ∆h(T) tunnetaan, voidaan myös laskea lämpökapasiteetti vakiopaineessa, koska C P =(∂H/∂T) P,N .

106 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAAIdeaalikaasulleP kin V vapaa = k B NT, (6.18)missä P kin on molekyylien kineettisestä energiasta johtuva paine ja V vapaa on tilavuus,jossa molekyylit voivat vapaasti liikkua. Ideaalikaasulle systeemin kineettinenenergia E kin on sama kuin kokonaisenergia E tot , mutta vuorovaikuttavalleaineelleE tot = E kin + E vv ,missä E vv on vuorovaikutusenergia. Koska jokainen molekyyli vuorovaikuttaakaikkien potentiaalin efektiivistä kantamaa lähempänä olevien molekyylienkanssa ja koska näiden molekyylien lukumäärä on verrannollinen niidenlukumäärätiheyteen N/V, voidaan olettaa, että vuorovaikutusenergia( NE vv ∝ − N,V)missä miinus-merkki on seurausta potentiaalin attraktiivisesta luonteesta. Toisaaltapaine P ∝ E/V, joten( ) N 2P = P kin − a ; a = vakio. (6.19)VJos kukin molekyyli vie tilavuuden b, on molekyylien liikkeeseen vapaata tilaaV vapaa = V − Nb. (6.20)Sijoitetaan P kin ja V vapaa yhtälöistä (6.19) ja (6.20) yhtälöön (6.18):[( ]N2P+a (V − Nb) = k B NT. (6.21)V)Jos tiheys vielä lausutaan molekyylitilavuuden v avulla v ≡ V/N = 1/ρ, saadaanvan der Waalsin tilanyhtälö yksinkertaiseen muotoon(P+ av 2 )(v−b) = k B T. (6.22)Saimme myös parametreille a ja b fysikaalisen tulkinnan: a liittyy molekyylienvälisen vuorovaikutuksen voimakkuuteen ja b on molekyylin “koko”. Van derWaalsin tilanyhtälö voidaan helposti yleistää myös seoksille.6.8.2 Stabiilisuus ja kriittinen pistePiirretään van der Waalsin tilanyhtälön (6.22) mukaisia isotermejä (v, P)-tasoon (kuva 6.10). Kuvasta havaitaan ensinnäkin, että riittävän matalissalämpötiloissa (T < T c ) isotermeillä on lokaali maksimi ja lokaali minimi. On

6.8. FAASIMUUTOKSET JA VAN DER WAALSIN TILANYHTÄLÖ (7.2, 7.3)107PP cCv cT > T cT = T cT < T cv = V/NKuva 6.10: Van der Waalsin yhtälön isotermejä.siis mahdollista löytää pistepareja (v 1 , v 2 ), joita vastaa sama paine. Tästä seuraa,että van der Waalsin tilanyhtälö pystyy kuvaamaan kaasun ja nesteen tasapainon.Kuvasta nähdään myös, että tietyn lämpötilan T = T c yläpuolellaisotermit ovat monotonisesti väheneviä. C on kriittinen piste (P c , v c ) ja T c onkriittinen lämpötila. Kriittisen pisteen yläpuolella aine on homogeenista fluidia,jossa faasiseparaatiota ei esiinny.Paineen riippuvuus tilavuudesta voidaan yhdistää aineen stabiilisuuteen,kun muistetaan, että termodynaamisesti stabiilille aineelle isoterminen kokoonpuristuvuusκ T > 0. Määritelmän (4.69) mukaanκ T = − 1 V( ) ∂V= − 1 ∂P T v( ) ∂v= − 1 ∂P T v1(∂P/∂v) T.Vertaamalla kuvan (6.10) käyrien kulmakertoimiin (= ∂P/∂v), tehdään seuraavatpäätelmät:⎧⎨ T > T c , κ T > 0 kaikkiallaJos T = T c ,⎩T < T c ,κ T → −∞ kriittisessä pisteessäκ T < 0, kun (∂p/∂v) > 0.Kriittisen pisteen alapuolella aine on siis epävakaa alueessa, jossa paine kasvaatilavuuden myötä.Kriittisen pisteen kautta kulkevalla isotermillä on kriittisessä pisteessä derivaatannollakohta,( ) ∂P= 0 (6.23)∂v T cja käännepiste,( ∂ 2 P∂v 2 )T c= 0. (6.24)Näistä ehdoista voidaan ratkaista kriittisen pisteen koordinaatit. Kirjoitetaan

108 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAAvan der Waalsin tilanyhtälö muotoonP = k BTv−b − av 2 (6.25)ja sovelletaan ehtoja (6.23) ja (6.23). Ensimmäisen derivaatan nollakohtaantaaToisen derivaatan nollakohdastasaadaanYhtälöistä (6.26) ja (6.27) ratkaistaan∂p∂v = − k BT(v−b) 2 + 2av 3 = 0k B T c = 2a (v c−b) 2. (6.26)v 3 c∂ 2 p∂v 2 = 2k BT(v−b) 3 − 6av 4 = 0k B T c = 3a (v c−b) 3. (6.27)v c = 3b.Kun v c sijoitetaan esimerkiksi yhtälöön (6.26), saadaanTilanyhtälöstä voidaan nyt ratkaistav 4 ck B T c = 8 a27 b .P c = 1 a27 b 2 .Van der Waalsin aineen kriittisen pisteen koordinaatit ovat sitenv c = 3b (6.28)k B T c = 8 a27 b(6.29)P c = 1 a27 b 2 . (6.30)Kriittisen pisteen paikka riippuu vain tilanyhtälön ainevakioista a ja b, eli ainevakiotvoidaan määrätä, jos kriittinen piste tunnetaan.Ideaalikaasun tilanyhtälö lausuu paineen riippuvuuden tilavuudesta jalämpötilasta universaalissa eli ainevakioista riippumattomassa muodossa. Joshalutaan tilanyhtälö, joka kuvaa sekä kaasu- että nestefaasia, ei täysin aineesta

6.8. FAASIMUUTOKSET JA VAN DER WAALSIN TILANYHTÄLÖ (7.2, 7.3)109Aine T c (K) z cNe 44,8 0,305Ar 150,7 0,292Kr 209,4 0,290Xe 289,8 0,288N 2 126,0 0,292O 2 154,3 0,292CO 133,0 0,294CH 4 190,3 0,289H 2 O 647,4 0,229Taulukko 6.2: Eräiden aineiden kriittisiä lämpötiloja ja kokoonpuristuvuustekijöitä.riippumatonta tilanyhtälöä voida kirjoittaa. Van der Waalsin tilanyhtälö voidaankuitenkin ilmaista eräällä tapaa universaalissa muodossa redusoitujenmuuttujien¯P = P/P c ; ¯T = T/T c ; ¯v = v/v cavulla. Sijoittamalla nämä yhtälöön (6.22) saadaan dimensioton van der Waalsinyhtälö(¯P+ 3¯v )(2 ¯v− 1 )= 8 3 3 ¯T, (6.31)jossa ainevakiot eivät esiinny. Yhtälö (6.31) ilmaisee vastaavien tilojen lain(law of corresponding states): samoissa olosuhteissa ( ¯P, ¯T, ¯v) kaikki fluiditkäyttäytyvät samalla tavalla.Kirjoitetaan nyt tilanyhtälö (ei välttämättä van der Waalsin tilanyhtälö)muotoon z = Pv/k B T, missä z on kokoonpuristuvuustekijä. Redusoitujen muuttujienavulla:z = ¯PP c ¯vv ck B ¯TT c= P cv c¯P ¯vk B T c¯T = z ¯P ¯vc¯T . (6.32)Yhtälön (6.32) mukaan vastaavien tilojen laki pätee kaikille aineille, jos kriittinenkokoonpuristuvuustekijä z c sama. Van der Waalsin aineelle z c = 3/8 =0, 375. Vertaamalla taulukon 6.2 kokeellisiin tuloksiin havaitaan, että van derWaalsin tilanyhtälö jossain määrin yliarvioi kokoonpuristuvuustekijän kriittisessäpisteessä. Huomataan myös, että z c ei ole vakio. Pyöreähköille ja eipolaarisillemolekyyleille kokoonpuristuvuustekijä onz c ≈ 0, 29, mutta polaarisilleja muodoltaan huomattavasti pallomaisesta poikkeaville molekyyleillekokoonpuristuvuustekijä on pienempi. Tämä tarkoittaa, että ei ole mahdollistalöytää yleistä tilanyhtälöä ¯P = f( ¯T, ¯v), joka kuvaisi kvantitatiivisesti oikeinaineen termodynaamisia ominaisuuksia kriittisen pisteen lähellä tai ylipäänsäkorkeassa paineessa. Tarkemmissa tilanyhtälöissä joudutaankin turvautumaan

110 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAAvv kv nBECIAIIDPKuva 6.11: Maxwellin konstruktio.lisäparametrien käyttöön. Van der Waalsin tilanyhtälö antaa kuitenkin laadullisestioikeita ennusteita ja on siksi riittävä tarkasteltaessa monia faasimuutoksiinliittyviä ilmiöitä.6.8.3 Maxwellin konstruktioKuvan 6.10 mukaan kun lämpötila on kriittistä lämpötilaa alempi T < T c onmahdollista löytää lukupareja(v k , v n ), joista toinen, v k , sijaitsee harvan aineenpuolella (höyry) ja toinen, v n tiheän aineen puolella (neste), ja jotka molemmatvastaavat samaa painetta. Mutta miten näistä pareista voidaan löytää se, jokakuvaa nesteen ja höyryn tasapainoa?Gibbsin ja Duhemin yhtälön (4.39) mukaandµ = −( SN)dT+( VN)dP = −sdT+ vdP.Jos nyt tarkastellaan yhtä kuvan 6.10 isotermiä, on dT = 0 jadµ = vdP. (6.33)Yhtälö (6.33) voidaan integroida nesteestä kaasuun pitkin isotermiä, ja kunmuistetaan, että tasapainoehtojen mukaan µ k = µ n , saadaan∫ µkµ ndµ = µ k − µ n =∫ vkv nvdP = 0.Integrandi v(P) on moniarvoisuutensa vuoksi hieman hankala, ja siksi onkinparasta turvautua geometriseen tarkasteluun. Vaihdetaan v- ja P-akselienpaikat ja jaetaan integraali kuvan 6.11 mukaisesti neljään osaan:∫ vkv nvdP =+∫ BA∫ DC∫ CvdP+vdP+B∫ EDvdPvdP= Ala I−Ala II. (6.34)

6.8. FAASIMUUTOKSET JA VAN DER WAALSIN TILANYHTÄLÖ (7.2, 7.3)111TCρ = N/VKuva 6.12: Binodal (yhtenäinen viiva) ja spinodal (katkoviiva). Harmaa alueon epästabiili.Tasapainotila siis löydetään, kun alat I ja II asetetaan yhtä suuriksi. Tätä kutsutaanMaxwellin konstruktioksi.Maxwellin konstruktion käyttö edellyttää, että tilanyhtälö tunnetaan.Muussa tapauksessa tasapaino-ominaisuuksien määrittäminen hankaloituu,mutta esimerkiksi tasapainohöyrynpaine voidaan approksimoida Clausiuksenja Clapeyronin yhtälöstä. Vaihtoehtoisesti faasitasapaino voidaan löytää ratkaisemalla(numeerisesti) samanaikaiset ehdot P(v k ) = P(v n ) ja µ(v k ) = µ(v n ).6.8.4 Epästabiilit ja metastabiilit tilatKun Maxwellin konstruktion tai muun menetelmän avulla löydetyt eri isotermejävastaavat molekyylitilavuudet tai tiheydet höyry-neste tasapainossapiirretään lämpötilan funktiona, muodostavat ne ns. binodal-käyrän. Kuvassa6.12 binodal on esitetty (ρ, T)-tasossa (yhtenäinen viiva). Painekäyrän lokaalitminimi- ja maksimikohdat (dp/dv = 0) määrittelevät spinodal-käyrän, kuvassa6.12 katkoviivalla esitetty käyrä. Käyrät sivuavat kriittisessä pisteessä C.Harmaassa alueessa kokoonpuristuvuus on negatiivinen ja aine on epästabiili.Epästabiiliin tilaan joutunut aine romahtaa väistämättä takaisin stabiiliin tilaan.Epästabiili tila on olemassa vain hetkellisesti, eikä sen ominaisuuksia voikuvata termodynamiikan keinoin.Binodal- ja spinodal-käyrien väliin jäävä alue on metastabiili. Tässä alueessaaine on stabiili pienten fluktuaatioiden suhteen, suuret fluktuaatiot sen sijaanjohtavat faasimuutokseen. Metastabiiliin kaasuun syntyy pieniä molekyyliryppäitä,nestefaasiin taas kuplia. Ilmiötä kutsutaan nukleaatioksi, ja se on ensimmäisenkertaluvun faasimuutoksen alkuaskel. Pienten uuden faasin alkioidenon ylitettävä energiakynnys ennen kuin ne voivat kasvaa makroskooppisiksipisaroiksi tai kupliksi, muutoin ne hajoavat ja palautuvat alkuperäiseenfaasiin. Metastabiilissa alueessa faasialkiolle on energeettisesti edullista siirtyästabiiliin faasiin, mutta toisaalta pinnanmuodostus vanhan ja uuden faasinvälille vaatii energiaa. Vasta, kun edellinen energiakontribuutio on itseisarvoltaanjälkimmäistä suurempi, voi faasialkio kasvaa “rajatta”. Tietenkin suljetus-

112 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAAV n , TrV k , ThöyryäKuva 6.13: Pisara tasapainossa höyryn kanssa.sa systeemissä faasialkioiden kasvu muuttaa vanhan faasin tiheyttä niin, ettälopulta kasvu pysähtyy.6.9 Pisaran tarina, osa 3: Tasapainoehdot ja muodostumisenvapaa energia mitattavien suureidenavullaTähän mennessä luvussa 6 on tarkasteltu tasopinnan erottamia faaseja. Palaammenyt pallomaiseen nestepisaraan kaasussa, jolle johdimme tasapainoehdotkappaleessa 4.12 ja muodostumisen vapaan energian kappaleessa 5.5.Tässä kappaleessa lausumme paineiden tasapainoehdon eli Laplacen yhtälön(4.86) ja pisaran muodostumisen vapaan energian muutoksen (5.43) sellaisessamuodossa, että esiintyvät suureet ovat helposti mitattavia ja siten yleisestitaulukoituja. Historiallisista syistä puhumme Gibbsin vapaan energian muutoksesta,vaikka näimme kappaleessa 5.5, että Helmholtzin vapaan energian jasuuren potentiaalin muutokset ovat itseasiassa yhtä suuria kuin Gibbsin vapaanenergian muutos kunhan höyryä on pisaran sisältämiin molekyyleihinverrattuna hyvin paljon.6.9.1 Kelvinin yhtälöPisaran kanssa tasapainossa olevan höyryn paine voidaan laskea tasopinnantasapainohöyrynpaineen ja pisaran säteen funktiona lähtien LaplacenyhtälöstäP n − P k = 2σ r(6.35)ja kemiallisten potentiaalien yhtäsuuruudesta (4.85)µ k (P k , T) = µ n (P n , T)(= µ p ).

6.9. PISARAN TARINA, OSA 3: TASAPAINOEHDOT JA MUODOSTUMISENVAPAA ENERGIA MITATTAVIEN SUUREIDEN AVULLA 113Tässä rajoitumme yksinkertaisuuden vuoksi yhden komponentin systeemiin.Gibbsin ja Duhemin yhtälön (4.39) mukaandµ = vdP− sdT,missä v = V/N ja s = S/N . Kirjoittamalla Gibbsin ja Duhemin yhtälö erikseenhöyrylle ja pisaralle ja ottamalla huomioon, että tasapainossa höyryn ja pisarankemialliset potentiaalit ovat samat eli dµ k = dµ n ja että dT = 0, saadaanjosta ratkaistaanv n dP n = v k dP k ,dP n = v kv ndP k . (6.36)Useamman komponentin tapauksessa käytetään Maxwellin yhtälöä (5.13), jostasaadaandµ i⏐ ⏐⏐⏐xi,T= v i dP,ja päästään samankaltaiseen tulokseen.Toisaalta Laplacen yhtälöstä (6.35) differentioimallaseuraa ( ) 2σdP n − dP k = d . (6.37)rYhtälöistä (6.36) ja (6.37) saadaan( ) (vk − v n2σdPv k = dn r). (6.38)Pintajännitys riippuu lämpötilasta. Guggenheim (1945) on esittänyt empiirisenkorrelaationσ(T) = σ 0 (1− T/T c ) n , (6.39)missä σ 0 ja n ovat sovitusparametreja ja T c on kriittinen lämpötila. Pisaran tapauksessapintajännitys riippuu myös pisaran säteestä, millä on merkitystäkun pisara on hyvin pieni. Tiedetään, että v n ≪ v k , joten v k − v n ≈ v k . Kunlisäksi oletetaan, että höyry on ideaalikaasua, on v k = k B T/P k , ja yhtälö (6.38)tulee muotoonk B Tv ndP kP k= d( 2σr). (6.40)Oletetaan nesteen molekyylitilavuus v n vakioksi paineenvaihteluiden suhteen.Näin voidaan tehdä, koska nesteet ovat yleensä lähes kokoonpuristumattomia.Kun vielä unohdetaan pintajännityksen kokoriippuvuus, voidaan yhtälö (6.40)integroida äärettömän pisaran rajalta (tasopinta) r-säteiseen pisaraan:k B Tv n∫ Pk,sat (r)P k,sat (∞)dP kP k∫ r( ) 1= 2σ d∞ r ′ ,

114 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAAP k (R)Kuva 6.14: Tasapainohöyrynpaine pisaran säteen funktiona.Rjosta saadaan Kelvinin yhtälöP k,sat (r) = P k,sat (∞) exp( ) 2σvn. (6.41)k B TrTästä nähdään, että tasopintaa vastaava tasapainohöyrynpaine P k (∞) on ainapienempi kuin sen höyryn paine, jonka kanssa pisara on tasapainossa. Tasapainohöyrynpaineenriippuvuus pisaran säteestä on esitetty kaavamaisestikuvassa 6.14.Fysikaalinen tulkinta tälle ns. Kelvinin efektille saadaan, kun verrataan molekyyliensijoittumista nestepinnalla pisaran ja tasopinnan tapauksessa. Pisaranpinnalla molekyyli kokee toisten molekyylien aiheuttaman attraktiivisenvuorovaikutuksen heikommin kuin tasopinnalla, koska kaareutumisen vuoksinaapurimolekyylejä on vähemmän. Jos tarkasteltavan molekyylin kohdallekuvitellaan tangenttitaso, sijaitsevat tasopinnan naapurimolekyylit tällä tasolla,kun taas pisarassa molekyylit jäävät tason “alapuolelle” (kuva 6.15) ja sitenne tavallaan “näkevät” pisaraa ympäröivän kaasun laajemmassa kulmassa.Tästä syystä pintamolekyylit karkaavat helpommin kaasufaasiin ja tarvitaansuurempi höyrynpaine (tiheämpi höyry) estämään pisaran vähittäinen haihtuminen.Kelvinin yhtälö voidaan myös kirjoittaa muotoonr =2σv nkT ln(P k /P k,sat (∞)) , (6.42)joka kertoo, että tietylle aineelle vakiolämpötilassa ja vakiohöyrynpaineessaP k vain r-säteiset pisarat voivat olla tasapainossa höyryn kanssa. Suuremmatpisarat jatkavat tiivistymällä kasvua “rajatta” ja poistuvat höyrystä, kun taaspienemmät pisarat haihtuvat takaisin höyryksi.Kelvinin yhtälöllä on suuri merkitys aerosolifysiikassa, joka tutkii pieniä ilmassaleijuvia nestemäisiä tai kiinteitä hiukkasia. Tyypillisesti Kelvinin efektion otettava huomioon, jos pisaran läpimitta on pienempi kuin 50 nm. Kuitenkinesimerkiksi suurimolekyylisistä orgaanisista yhdisteistä koostuville pisaroillevoi Kelvinin efekti olla merkittävä jo, kun pisaran läpimitta on 200 nm.

6.9. PISARAN TARINA, OSA 3: TASAPAINOEHDOT JA MUODOSTUMISENVAPAA ENERGIA MITATTAVIEN SUUREIDEN AVULLA 115Kuva 6.15: Molekyylien sijoittuminen pisaran pinnalla.Pisaran ja kaasun tasapainoa tarkasteltaessa on syytä huomata, että toinensysteemin osasista ei saavuta termodynaamista rajaa, nimittäin nestepisara.Termodynaamisen käsittelyn kannalta onkin ymmärrettävä, että tässä pisaraaei voida käsittää todellisena fysikaalisena objektina vaan hypoteettisena nestepisarana,jolla on tasapainovaatimusten mukainen kemiallinen potentiaali.Tästä seuraa muun muassa, että hyvin pienelle pisaralle Laplacen yhtälöstälaskettu paine pisaran sisällä (joka voi olla hyvin suuri, laske!) on tämän hypoteettisennestefaasin paine. Paine todellisen fysikaalisen pisaran sisällä on aivanjotain muuta (jos se on edes hyvin määritelty). Kuitenkin termodynaaminenmenetelmä pystyy kuvaamaan varsin pieniäkin pisaroita tai muita vastaaviaobjekteja kohtalaisen hyvin. Tässä suhteessa termodynamiikka on varsinanteeksiantava teoria.6.9.2 Muodostumisen vapaa energiaPyrimme nyt muokkaamaan pisaran muodostumisen vapaan energian sellaiseenmuotoon, että voimme piirtää vapaan energian pisaran säteen funktiona,ja tästä käyrästä päätellä minkä säteinen pisara on tasapainossa tietyn paineisenja lämpötilaisen kaasun kanssa , ja millaisesta tasapainosta on kyse. Saaduntasapainokoon on tietenkin oltava sama kuin Laplacen tai Kelvinin yhtälöstäsaatu tulos, koska kyse on samojen periaatteiden soveltamisesta termodynamiikankoneistoa hiukan eri tavalla käyttäen. Muodostumisenergiaa tarkasteltaessasaadaan kuitenkin lisätietoa Laplacen tai Kelvinin yhtälön käyttöön verrattuna,sillä nyt saadaan tietoa myös tasapainopisaran muodostumiseen vaadittavasta(vapaasta) energiasta, josta voidaan johtaa myös pisaran muodostumistodennäköisyys.Muodotumistodennäköisyyslaskut ovat kuitenkin tämänkurssin rajauksen ulkopuolella.Vakiolämpötilassa Gibbsin ja Duhemin yhtälö yhden komponentin systeemillekuuluu dµ = vdP. Kun tämä kirjoitetaan nesteelle, ja oletetaan jälleenneste kokoonpuristumattomaksi, ja integroidaan kaasun paineesta nesteen paineeseenjosta saadaan∫ PnP kdµ n =∫ PnP kv n dP, (6.43)µ n (P n )−µ n (P k ) = v n (P n − P k ) (6.44)

116 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAAKertomalla tämä nesteessä olevien molekyylien määrällä −N n ja käyttäen yhteyttäN n v n = V n päästään tulokseen−[µ n (P n )−µ n (P k )]N n = V n (P k − P n ).Muodostumisen vapaan energian lausekkeessa (5.43) esiintyy juuri tämätermi (kun merkitään P 0 = P k ) joten saadaan∆G= (P k − P n )V n + σA+(µ n − µ k )N n +(µ p − µ k )N p= −[µ n (P n )−µ n (P k )]N n + σA+(µ n (P n )−µ k )N n +(µ p − µ k )N p= (µ n (P k )−µ k )N n + σA+(µ p − µ k )N p . (6.45)Nyt pitäisi päästä eroon pintamolekyylien määrästä N p . Tämä molekyylimääräon kytköksissä siihen, miten pisaran raja on määritelty. Tosiasiassa pisaranreunamilla fluidi harvenee vähitellen nesteen tiheydestä kaasun tiheyteen,eikä voida tarkasti ottaen sanoa, missä pisara loppuu ja kaasu alkaa.Pisaran säteen valinta on siis jossain rajoissa mielivaltainen. Ilman mielivaltaisuutta(ja nimellisen säteen valinnasta riippumatta) voidaan kuitenkin laskeakuinka monta molekyyliä pisaran sisältävässä tilavuudessa on enemmänkuin jos koko tuo tilavuus olisi täytetty homogeenisella kaasulla. Pisaran tilavuudensisältämän kaasun molekyylien määrä on mitätön pisaran molekyylimääräänverrattuna jo useasti käytetyn tiedon v k >> v n perusteella,joten se voidaan jättää huomiotta. Merkitään pisaran sisältämien molekyylientodellista määrää N tot . Termodynaamisessa nestepisaramallissa oletetaan,että r-säteisen pisaran sisällä on nesteen tiheys ja sen ulkopuolella kaasun tiheys.Molekyylien määrä tässä mallipisarassa on N n = 4/3πr 3 /v n , ja se riippuusiis valitusta säteestä r. Pintamolekyylien määrä asetetaan sellaiseksi, ettäN tot = N n (r:n valinta)+ N p (r:n valinta). Tavallisesti yksikomponenttisessa pisaramallissavalitaan pisaran nimellinen säde siten että N p = 0. Useampienkomponenttien muodostamissa pisaroissa tätä ehtoa ei voi toteuttaa kaikkienkomponenttien kohdalla yhdellä säteen r valinnalla, ja silloin käytetään ehtoa∑ N i,p v i,n = 0,ijoka yhdelle komponentille antaakin N p = 0. Tätä valintaa kutsutaan tasamoolipinnaksi(englanniksi equimolar surface). Valitsemalla tasamoolipinta pisaransäteen määritelmäksi muodostumisen vapaa energia saadaan yksinkertaiseenmuotoon∆G = (µ n (P k )−µ k )N n + σA.Nyt meidän on vielä lausuttava kemiallisten potentiaalien erotus µ n (P k )−µ k mitattavien suureiden avulla. Tämä tapahtuu siten, että sekä µ n (P k ) ettäµ k = µ k (P k ) lausutaan tasapainossa olevien nesteen ja kaasun kemiallisten potentiaalienavulla, jotka ovat tasapainoehdon vuoksi tietenkin yhtäsuuret. Onhuomattava, että µ n (P k ) ei ole pisarassa olevan nesteen kemiallinen potentiaali,koska se ei ole nesteen paineessa, vaan kaasun paineessa. Todellinen nesteenkemiallinen potentiaali µ n (P n ) supistui pois yhtälössä (6.45). Sijoittamalla

6.9. PISARAN TARINA, OSA 3: TASAPAINOEHDOT JA MUODOSTUMISENVAPAA ENERGIA MITATTAVIEN SUUREIDEN AVULLA 117yhtälössä (6.44) nesteen paineen tilalle kassun paine ja kaasun paineen tilallekylläisen höyryn paine (tasopinnan yläpuolella) P k,sat saadaan nesteen kemiallisillepotentiaaleille relaatioµ n (P k )−µ n (P k,sat ) = v n (P n − P k,sat ). (6.46)Kaasulle voidaan kirjoittaa yhtälöä (6.43) vastaavasti∫ PkP k,satdµ k =∫ PkP k,satv k dP,johon ideaalikaasulaista sijoitetaan v k = kT/P k , jolloin kaasun kemiallisille potentiaaleillesaadaan relaatioµ k (P k )−µ k (P k,sat ) = kT ln P kP k,sat. (6.47)Pidetään mielessä, että tasapainoehdon nojalla µ n (P k,sat ) = µ k (P k,sat ), jolloinvähentämällä yhtälöt (6.46) ja (6.47) toisistaan saadaanµ n (P k )−µ k (P k ) = −kT ln P kP k,sat+ v n (P k − P k,sat ).Tehdään yksinkertainen suuruusluokkatarkastelu: Ilmakehän olosuhteissaesimerkiksi vedelle (suhteellinen kosteus 100 %, lämpötila 298 K) P k − P k,sat ≈10 4 Pa, veden molekyylitilavuus nesteessä v n = 10 −30 m 3 ja Boltzmannin vakiok = 1.38·10 −23 J/K. Tästä nähdään, että kT lnP kP k,sat≈ 10 −21 J ja v n (P k −P k,sat ) ≈ 10 −26 J, joten yhtälön (6.9.2) jälkimmäinen termi on mitättömän pieniensimmäiseen termiin verrattuna , ja lopulta muodostumisen vapaa energiavoidaan kirjoittaa käytännölliseen muotoon∆G = −N n kT lnP kP k,sat+ σA.Kirjoittamalla pallon tilavuuden ja pinta-alan lausekkeet V n = N n v n =4/3πr 3 ja A = 4πr 2 voidaan muodostumisen vapaa energia nyt piirtääjoko säteen r tai molekyylien lukumäärän N n funktiona tietyssä valitussalämpötilassa ja höyryn osapaineessa P k . Esimerkiksi lausumalla molekyylienlukumäärä säteen avulla saadaan∆G = − 4 kTπr3 lnP k+ 4πσr 2 . (6.48)3 v n P k,satKylläiselle höyrynpaineelle ja pintajännitykselle (jotka ovat yksikomponenttisysteemissävain lämpötilan funktioita) löytyy monille aineille arvojaja mittaustuloksiin sovitettuja yhtälöitä taulukkokirjoista. Kuvassa 6.16on piirretty muodostumisen vapaan energia vesipisaralle säteen funktionalämpötilassa 298 K ja kahdessa eri vesihöyryn osapaineessa, joita vastaavatsuhteelliset kosteudet ovat 300% ja 500%.

118 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAA7060P g/P g,sat=5P g/P g,sat=3vesi, T=298 K50∆ G /(kT)4030201000.3 0.4 0.5 0.6 0.7 0.8 0.9 1r[nm]Kuva 6.16: Muodostumisen vapaa energia vesipisaralle pisaran säteen funktionakahdessa eri vesihöyryn osapaineessa.Kuvasta todetaan, että muodostumisen vapaalla energialla ei olekaan minimiä,kuten vakaassa tasapainossa pitäisi vaan maksimi. Tämän maksiminpaikan antaa Kelvinin yhtälö (6.42) tai yleisemmin Laplacen yhtälö (6.35) Tasapainopisaraonkin epävakaassa tasapainossa: jos siitä lähtee molekyylejä pois,se haihtuu takaisin höyryksi, ja jos siihen lisätään molekyylejä, se kasvaa rajattakunnes höyry loppuu tai pisara tulee niin painavaksi että se lähtee putoamaanalas painovoiman vaikutuksesta. Pienillä pisaroilla kasvaminen edellyttääsiirtymistä ylöspäin vapaassa energiassa. Nämä pisarat ovatkin taipuvaisiahaihtumaan höyryksi. Yhtälön (6.48) ensimmäinen tilavuustermi (∝ r 3 )on ylikylläisessä höyryssä negatiivinen kuvaten sitä, että neste on näissä olosuhteissavakaa eli vapaalta energialtaan alempi faasi. Pinnan muodostaminenkahden faasin välille maksaa kuitenkin energiaa, ja tätä kuvaa yhtälönjälkimmäinen pintatermi (∝ r 2 ). Pisaran säteen on kasvettava riittävän suureksi,ennenkuin faasitransitiossa saavutettu hyöty kumoaa pinnanmuodostuksestaaiheutuvan sakon. Vesimolekyylien törmäilyt pisaraan ja toisaalta molekyylienirtoaminen pisarasta kilpailevat keskenään, ja koska kyse on satunnaisprosesseista,on mahdollista että pisara saavuttaa tasapainokoon eli niinsanotun kriittisen koon siitä huolimatta että se joutuu kiipeämään vapaan energianylämäkeen. Kriittisen koon saavuttanut pisara on nukleoitunut. Käyristänähdään, että tasapainopisaran säde on sitä suurempi, mitä alempi on vesihöyrynosapaine, ja myös nukleaatiovalli eli vapaan energian valli, jonkapäälle pisaran on kiivettävä, on korkeampi alemmassa veden osapaineessa. Joshöyryn osapaine on kylläinen höyrynpaine tai sitä alempi, kuvan 6.16 käyrillä

6.9. PISARAN TARINA, OSA 3: TASAPAINOEHDOT JA MUODOSTUMISENVAPAA ENERGIA MITATTAVIEN SUUREIDEN AVULLA 119ei ole maksimia vaan ne jatkavat nousuaan ylöspäin rajattomasti. Tällöin nestefaasiei ole stabiili faasi. Tätä vastaa kuvassa (6.10) se T < T C -käyrän osakorkealla molekyylitilavuudella v, jossa kutakin painetta vastaa vain yksi molekyylitilavuus,eli tiheydet binodalin oikealla puolella kuvassa (6.12). Jos vesihöyrynosapaine on tarpeeksi suuri, maksimi häviää ja käyrät suuntautuvatalusta asti alaspäin. Tällöin kaasu ei ole enää metastabiili faasi vaan neste onainoa millään tavalla vakaa aineen tila. Tätä vastaa kuvassa (6.10) se T < T Ckäyrän osa alhaisella molekyylitilavuudella v, jossa kutakin painetta vastaavain yksi molekyylitilavuus, eli tiheydet binodalin vasemmalla puolella kuvassa(6.12).Derivoimalla yhtälöä (6.48) säteen r suhteen saadaan∂∆G∂r⏐⏐Pk ,T= − 4π 3kT3r2 lnP k+ 8πσrv n P k,sat= −4πr 2 kT lnP k+ 8πσr. (6.49)v n P k,satKun tämä asetetaan nollaksi, saadaan tasapainopisaralle (joka merkitään nytyläindeksillä ∗ )r ∗ =2σv nkT ln(P k /P k,sat ) , (6.50)eli Kelvinin yhtälö (6.42). Aiemmin johdimme Kelvinin yhtälön Laplacenyhtälöstä, joka puolestaan johdettiin kappaleessa 4.12 entropian differentiaalinnollakohdasta. Nyt näemme että saman tuloksen saamme etsimällä muodostumisenvapaan energian differentiaalin nollakohdan, kuten pitääkin.Nukleaatiovallin korkeus eli kriittisen klusterin muodostumisen vapaaenergia saadaan laskettua sijoittamalla tulos (6.50) vapaan energian lausekkeeseen(6.48). Helpoimmin tämä tapahtuu sijoittamalla kT ln(P k /P k,sat ) =2σv n /r ∗ lausekkeeseen (6.48) jolloin saadaan∆G = − 4 3 πr∗3 1 v n2σv nr ∗ + 4πσr ∗2 = 4 3 πr∗2 σ,missä r ∗ saadaan yhtälöstä (6.50) .Lasketaan vielä nukleaatiovallin korkeuden derivaatta kaasun osapaineenP k suhteen vakiolämpötilassa muistaen, että kylläinen höyrynpaine P k,sat , pintajännitysσ ja nesteen molekyylitilavuus v n ovat vakiolämpötilassa vakioitayksikomponenttisysteemissä. Derivaatta on helpompi ottaa ln P k :n kuin P k :nsuhteenjoten laskettavaksi tulee∂r ∗∂ ln P k⏐ ⏐⏐⏐T=∂∆G ∗ ⏐ ⏐⏐⏐T= 8 ∂r ∗ ⏐ ⏐⏐⏐T∂ ln P k 3 πσr∗ ∂ ln P k⏐−2σv n ∂ ln(P k /P k,sat ) ⏐⏐⏐TkT[ln(P k /P k,sat )] 2 =∂ ln P k−2σv nkT[ln(P k /P k,sat )] 2

120 LUKU 6. FAASIEN JA FAASIMUUTOSTEN TERMODYNAMIIKKAAkoska∂ ln(P k /P k,sat )∂ ln P k⏐ ⏐⏐⏐T= ∂(ln P k− ln P k,sat )∂ ln P k⏐ ⏐⏐⏐T= 1.Nukleaatiovallin korkeuden derivaataksi saadaan∂∆G ∗ ⏐ ⏐⏐⏐T= − 8 2σv n∂ ln P k 3 πσr∗ kT[ln(P k /P k,sat )] 2 = − 4 2 2 σ 2 v n3 πr∗ kT[ln(P k /P k,sat )] 2 .Tässä huomataan, että r ∗ :n jälkeen kirjoitettu osamäärä on tekijää v n /kT vaillayhtä suuri kuin r ∗2 . Lavennetaan tekijällä v n /kT, jolloin saadaan∂∆G ∗ ⏐ ⏐⏐⏐T= − 4 kTπr ∗∂ ln P k 3 v nKirjoitetaan tulos muotoon2 2 σ 2 v 2 n[kT ln(P k /P k,sat )] 2 = −kT 4v n 3 πr∗3 = −kTNn ∗ .∂ −∆G∗kT∂ ln P k⏐ ⏐⏐⏐T= N ∗ n ,joka on paljon käytetty ensimmäinen nukleaatioteoreema.Tämä tulos, jonka tässäjohdimme yksinkertaiselle pisaramallille, voidaan johtaa myös hyvin yleisistästatistisen mekaniikan tarkasteluista. Kineettisillä (ei termodynamiikan piiriinkuuluvilla) tarkasteluilla voidaan osoittaa, että pisaroiden muodostumisnopeus(aika-ja tilavuusyksikköä kohti) eli nukleaationopeus J ∝ exp( −∆G∗kT), jotenmitatun nukleaationopeuden logaritmin derivaatasta nukleoituvan höyrynosapaineen logaritmin suhteen voidaan päätellä kriittisen klusterin molekyylilukumäärä⏐∂ ln J ⏐⏐⏐T≈ Nn ∗ ∂ ln P .kTulos on tärkeä, koska sen avulla makroskooppisesta mittauksesta saadaantietoa molekyylitason ilmiöistä. Toinen nukleaatioteoreema kertoo yhteydennukleaationopeuden lämpötiladerivaatan (kun höyryn osapaine tai vaihtoehtoisestikyllästysaste pidetään vakiona) ja kriittisen klusterin sidosenergianvälillä.

Luku 7Liuosten termodynamiikkaa7.1 Partiaaliset molekyylisuureetEdellä esitetty termodynamiikan perusformalismi on suoraviivaisesti yleistettävissämonikomponenttisiin systeemeihin. Esimerkiksi termodynaamistenpotentiaalien differentiaalit säilyvät sellaisinaan, kunhan tehdään muutoksetµdN → ∑ i µ i dN i tai Ndµ → ∑ i N i dµ i . Yhdestä ainekomponentista koostuviensysteemien tiheyssuureita (tai ominaissuureita) vastaavat seoksissa partiaalisetmolekyylisuureet, jotka kertovat, miten seoksen ekstensiiviset ominaisuudetmuuttuvat, kun seokseen lisätään pieni määrä ainekomponenttia i komponenttienj ̸= i määrien pysyessä vakioina.Olkoon Y ekstensiivinen tilamuuttuja. Sen kokonaisdifferentiaali ondY =( ∂Y∂N 1)P,T,N 2 ,N 3 ,...Differentiaalien dN i kertoimety i ≡dN 1 +( ∂Y∂N i)( ∂Y∂N 2)P,T,N 1 ,N 3 ,...dN 2 + . . .P,T,N j̸=i, (7.1)ovat suureen Y partiaalisia molekyylisuureita. Ne ovat intensiivisiä suureita.Koska Y on ekstensiivinen suure ja koska hiukkasmäärät ovat myös ekstensiivisiä,on voimassa skaalausehtoY(λN 1 , λN 2 , . . .) = λY(N 1 , N 2 , . . .).Tästä voidaan helposti johtaa tulos (katso luku 4.7.1)Y = y 1 N 1 + y 2 N 2 + . . . (7.2)Suure Y voidaan siis lausua partiaalisten molekyylisuureiden ja hiukkasmäärienavulla.

122 LUKU 7. LIUOSTEN TERMODYNAMIIKKAAEsimerkkinä partiaalisista molekyylisuureista tarkastelemme partiaalisiamolekyylitilavuuksia kahden komponentin eli binäärisessä liuoksessa.Määritellään keskimääräinen molekyylitilavuusv =VN 1 + N 2. (7.3)Liuoksille usein tiedetään niiden massatiheys mooliosuuden ja lämpötilanfunktiona ρ m (x, T). Koskaρ m = m V = M 1N 1 + M 2 N 2, (7.4)Vmissä M 1 ja M 2 ovat molekyylien massat, saadaan ratkaisemalla tilavuusyhtälöstä (7.4) ja sijoittamalla yhtälöön (7.3)v = M 1N 1 + M 2 N 2N 1 + N 21ρ m= M 1x 1 + M 2 x 2ρ m. (7.5)Tästä nähdään, että myös v on lausuttavissa helposti mitattavien suureidenavulla. Partiaalinen molekyylitilavuus v 1 onv 1 =( ) ∂V= ∂( ) ∂v[v(N 1 + N 2 )] = (N 1 + N 2 ) + v. (7.6)∂N 1 N 2∂N 1 ∂N 1 N 2Tässä( ) ∂v= ∂v ( ) ∂x2∂N 1 N 2∂x 2 ∂N 1(= −N 2= ∂v∂x 2∂∂N 1(N2N 1 + N 2)x 2N 1 + N 2) ∂v∂x 2. (7.7)N 2Sijoittamalla tulos (7.7) yhtälöön (7.6) saadaanVastaavasti voidaan johtaav 1 = v− x 2∂v∂x 2. (7.8)v 2 = v−x 1∂v∂x 1= v+(1− x 2 ) ∂v∂x 2. (7.9)Käytännön sovellutuksissa on lausuttava keskimääräisen molekyylitilavuudenderivaatta mitattavan suureen eli liuoksen massatilavuuden avullalähtien kaavasta (7.5)

7.1. PARTIAALISET MOLEKYYLISUUREET 12358Etanolivvesi [cm 3 mol −1 ]1816Vesi5654v etanoli [cm 3 mol −1 ]140 0.2 0.4 0.6 0.8 1x etanoliKuva 7.1: Veden ja etanolin moolitilavuuksien riippuvuus etanolin mooliosuudestalämpötilassa 25◦C.[ ]∂v= ∂ M1 (1−x 2 )+M 2 x 2ρ m (x 2 )(7.10)∂x 2 ∂x 2= (−M 1+M 2 )ρ m − ∂ρ m∂X 2[M 1 (1− x 2 )+ M 2 x 2 ]ρ 2 m(7.11)= (M 2−M 1 )− 1 ∂ρ mρ m ρ 2 [M 1 (1− x 2 )+ M 2 x 2 ] (7.12)m ∂x 2= (M 2−M 1 )ρ m− 1ρ m∂ρ m∂x 2v (7.13)Liuosten termodynaamisissa sovelluksissa käytetään partiaalisten molekyylisuureidensijaan usein partiaalisia moolisuureita. Esimerkiksi partiaalinenmoolitilavuus määritelläänv i =( ∂V∂n i)P,T,n j̸=i, (7.14)missä n i on aineen i moolimäärä. Veden ja etanolin partiaaliset moolitilavuudetvesi-etanoliliuoksessa on esitetty kuvassa 7.1. Kuvasta nähdään, että moolitilavuuksienriippuvuus mooliosuudesta on hyvin monimutkainen.Vastaavalla tavalla kuin partiaalinen molekyylitilavuus voidaan määritelläpartiaaliset energiasuureet, entropia jne.

124 LUKU 7. LIUOSTEN TERMODYNAMIIKKAA7.2 Laimeiden liuosten höyrynpaineTarkastellaan liuosta, joka koostuu liuottimesta (engl. solvent) ja pienestämäärästä liuotettavaa ainetta (engl. solute). Liuotin voi olla esimerkiksi vesi.Olennaista on, että liuotettavaa ainetta on niin pieni määrä liuoksessa, että senmolekyylit ovat kaukana toisistaan eivätkä sitoudu aggregaateiksi, esimerkiksimiselleiksi, tai separoidu kokonaan eri faasiksi.Tasapainossa nesteen (n) ja höyryn (k) kemiallisten potentiaalien täytyy ollasamat sekä liuottimelle (w) että liuotettavalle aineelle (s):µ w,n = µ w,k (7.15)µ s,n = µ s,k . (7.16)Kun on kyse tasopinnasta, myös paineet ovat samat höyryssä ja nesteessä OlkoonP 0 puhtaan liuottimen tasapainohöyrynpaine ja P 0 + δP liuottimen tasapainohöyrynpaineliuospinnan yläpuolella. Koska liuotettavan aineen määräon pieni, voidaan liuottimen kemiallinen potentiaali kirjoittaa paine-eron δP jaliuottimen moolisosuuden muutoksen δx w potenssisarjana .Liuottimen kemiallinen potentiaali liuoksen tasapainohöyrynpaineessaP 0 + δP on siten kirjoitettavissa muotoon( ) ∂µwµ w (P 0 + δP, T, x w + δx w ) = µ w (P 0 , T, x w = 1)+ δx w∂x w T,P( ) ∂µw+ δP+O((δP) 2 ), (7.17)∂P T,x wmissä µ w (P 0 , T, x w = 1) = µ 0 w on puhtaan liuottimen kemiallinen potentiaali.Koska liuotettavan aineen vaikutus liuottimen ominaisuuksiin on pieni, voidaanyhtälössä (7.17) esiintyvä painederivaatta lausua puhtaan aineen ominaisuuksienavulla( ) ∂µw≈∂P T,x w( ∂µ0) (w ∂V0)= = V0≡ v 0∂P T,N w∂N w P,T Nw, (7.18)wmissä v 0 w on puhtaan liuottimen moolekyylitilavuus ja V 0 sen tilavuus.Yhtälön (7.18) toinen yhtäsuuruus seuraa Maxwellin relaatiosta(∂V/∂n) T,P =(∂µ/∂P) T,n (vrt. yhtälö (5.13)).Yhtälöstä (5.32)∆G mix = kT(N w ln x w + N p ln x p )

7.2. LAIMEIDEN LIUOSTEN HÖYRYNPAINE 125saadaan( ) ∂µw∂x wT,Pδx w = ∆µ mix,w =(∂∆Gmix∂N w)N p ,P,T[ ( ) ( ) ]1 ∂xw 1 ∂xp= kT ln x w + kT N w + N px w ∂N w N px p ∂N w N p[ ( ) ( ) ]∂xw ∂xp= kT ln x w + kT(N w − N p ) +∂N w N p∂N w N p= kT ln x w . (7.19)Tämä tulos pätee ideaalikaasulle ja nesteellekin, kun kyseessä on ns. ideaaliliuos.1Sijoittamalla saadut osittaisderivaatat yhtälöön (7.17) joka kirjoitetaan erikseenkaasulle ja nesteelle, ja sijoittamalla nämä tasapainoehtoon (7.15) saadaanµ w,k (P 0 , T, x w = 1)+kT ln x w,k + v 0 w,k δP k =µ w,n (P 0 , T, x w = 1)+kT ln x w,n + v 0 w,nδP n . (7.20)Paine tasopinnan erottamissa tasapainofaaseissa on sama sekä puhtaan aineen(P 0 ) että liuoksen tapauksessa. P 0 + δP n = P 0 + δP k,tot ≈ P 0 + δP w,kkun liuenneen aineen paine kaasussa on mitätön. Tällöin δP n = δP w,k ja merkitääntätä paine-eroa yksinkertaisesti δP. Puhtaan aineen tasapainoehdon nojallaµ w,k (P 0 , T, x w = 1) = µ w,n (P 0 , T, x w = 1), ja yhtälöstä (7.20) voidaan sitenratkaistakTδP =v 0 w,k − ln x w,n. (7.21)v0 w,n x w,kLiuottimen moolekyylitilavuus nesteessä on pieni verrattuna molekyylitilavuuteenkaasussa, eli v 0 w,l ≪ v0 w,g . Kun lisäksi oletetaan, että höyry noudattaaideaalikaasulakiasaadaan yhtälöstä (7.21)v 0 w,k = RT P ,δP = P ln x w,nx w,k= P(ln x w,n − ln x w,k ). (7.22)Yhtälön (7.22) ensimmäinen logaritmitermi voidaan kirjoittaa liuotettavan aineenmooliosuuden avulla:ln x w,n = ln(1− x s,n ) = −x s,n +O(x 2 s,n). (7.23)1 Ideaaliliuoksessa vuorovaikutuksen voimakkuus samanlaisten ja erilaisten molekyylienvälillä on keskimäärin sama. Ideaaliliuoksen ainekomponentille i pätee f i = x i f 0 i , missä f =exp(µ/(RT)) on fugasiteetti ja yläindeksi 0 viittaa puhtaaseen aineeseen.

126 LUKU 7. LIUOSTEN TERMODYNAMIIKKAAhLiuospaine = PH 2 O paine = P 0Kuva 7.2: Osmoosi.Kun otetaan huomioon vain yhtälön (7.23) ensimmäinen termi, ja oletetaan,että liuotettava aine ei juurikaan haihdu, ts. x w,k ≈ 1 eli ln x w,k ≈ 0 saadaanyhtälöstä (7.22) Raoultin lakiδPP = −x s,n. (7.24)Raoultin lain mukaan δP < 0 eli liuottimen tasapainohöyrynpaine on liuoksentapauksessa pienempi kuin puhtaan liuottimen tapauksessa.7.3 OsmoosiPuoliläpäisevä kalvo läpäisee liuottimen mutta ei liuotettavan aineen molekyylejä.Luonnossa puoliläpäiseviä kalvoja esiintyy erityisesti soluissa. Jospuoliläpäisevällä kalvolla suljetun putkilon pää asetetaan vesiastiaan ja putkiloonliuotetaan vähän esimerkiksi sokeria, havaitaan, että liuospinta putkilossaasettuu veden pintaa korkeammalle (kuva 7.2) Tämä osoittaa, että vettä onsiirtynyt astiasta putkiloon. Liuoksen ja nesteen pinnan välinen korkeusero hkertoo, että puhtaan veden ja liuoksen välillä on paine-ero, ns. osmoottinen paineP−P 0 = δP. Hydrostatiikan mukaisesti osmoottinen paine on δP = ρ m gh,missä ρ m on nesteen massatiheys.Termodynaamisesti on selvää, että yhtälön (6.1) mukaiset tasapainoehdoteivät ole voimassa sellaisenaan osmoottisessa systeemissä, koska liuotettavanaineen molekyylit eivät pääse kalvon läpi. Kalvo on jäykkä, joten se ei pystyvälittämään mekaanista energiaa, mikä fysikaalisesti ilmenee paine-erona vedenja liuoksen välillä. Tasapainossa puhtaan veden ja liuoksessa olevan vedenkemialliset potentiaalit ovat kuitenkin samat:µ w (P 0 , T, x w = 1) = µ w (P, T, x w ), (7.25)missä vasemmalla puolella on puhtaan veden kemiallinen potentiaali ja x w onveden mooliosuus liuoksessa. Yhtälön (7.25) oikea puoli käsitellään kuten edel-

7.3. OSMOOSI 127lisessä kappaleessa:µ w (P, T, x w ) = µ w (P 0 , T, x w = 1)+kT ln x w + v 0 w,n δP+...= µ w (P 0 , T, x w = 1)+kT ln(1− x p )+v 0 w,nδP+... (7.26)= µ w (P 0 , T, x w = 1)−kTx p + v 0 w,nδP+. . . , (7.27)missä x p on liuotettavan aineen mooliosuus. Kehitelmästä (7.27) puuttuvat termitkuvaavat liuottimen ja liuotettavan aineen molekyylien vuorovaikutuksestaaiheutuvaa kontribuutiota kemiallisen potentiaaliin.Yhdistämällä tulokset (7.25) ja(7.27) , ja toteamalla että puhtaan veden kemiallinenpotentiaali supistuu pois saadaanµ 0 w(P, T)− v 0 w,n δP = µ0 w(P, T)−kTx peliv 0 w,nδP = kTx p . (7.28)Koska laimeassa liuoksessa x p ≪ 1, on V 0 ≈ V, ja sitenv 0 w,n = V0N w≈ V N ,missä N on molekyylien kokonaismäärä. Nyt yhtälö (7.28) voidaan kirjoittaaeliVn δP ≈ kTx p = n pN kTδP ≈ kTN pV . (7.29)Tämä on van’t Hoffin yhtälö. Hieman yllättävästi se on muodoltaan ideaalikaasuyhtälö,mutta toisaalta tulos on järkevä, koska laimeassa liuoksessa liuotettavanaineen molekyylit ovat kaukana toisistaan eivätkä juuri vuorovaikutakeskenään.

Liite ATermodynaamistenderivaattojen käsittelystäTermodynaamisten ongelmien ratkaisu vaati usein termodynaamisten osittaisderivaattojenmuuttamista toiseen muotoon, muutenkin kuin vain Maxwellinrelaatioiden avulla. Vaikka tarvittavat muunnokset voidaan aina johtaa “alustaalkaen”, on seuraavassa esitettävistä yhtälöistä paljon hyötyä.Tarkastellaan funktiota x = x(y, z). Sen differentiaali ondx =( ) ∂xdy+∂yz( ) ∂xdz.∂z y(A.1)Vastaavasti, jos vapaiksi muuttujiksi valitaan x ja z, eli y = y(x, z),dy =( ) ∂ydx+∂x z( ) ∂ydz.∂z xYhtälön (A.2) avulla dx voidaan kirjoittaa muotoon( ) [( ) ( ) ] ( )∂x ∂y ∂y ∂xdx =dx+ dz +∂yz∂x z ∂z x ∂z( ) ( ) ( ) ( )∂x ∂y ∂x ∂y=dx+dz+∂y ∂x ∂y ∂zzViemällä dx- ja dz-termit yhtälön eri puolille saadaan[1−( ) ∂x∂yz( ∂y∂x)zz]dx =z[ ( ) ∂x∂yzx( ) ∂y+∂z xdzy( ∂x∂z( ∂x∂z)dz.y)]dz.y(A.2)(A.3)Yhtälössä (A.3) dx:ää ja dz:aa voidaan varioida toisistaan riippumatta, jolloinnäiden kertoimet (hakasulkulausekkeet) voidaan asettaa erikseen nolliksi.

129eliValitaan ensin dx ̸= 0 ja dz = 0. Yhtälöstä (A.3) saadaan1−( ) ∂x∂yz( ) ∂x=∂yz( ) ∂y= 0∂x z1) . (A.4)( ∂y∂xValitaan sitten dx = 0 ja dz ̸= 0. Tästä seuraa, että( ) ∂x∂yz( ) ∂y+∂z xz( ) ∂x= 0.∂z yJakamalla(∂x/∂z) y :llä ja käyttämällä yhtälöä (A.4) saadaan( ) ∂x∂yz( ) ∂y∂z x( ) ∂z= −1. (A.5)∂x yTämä tulos tunnetaan myös Eulerin permutaationa.Olkoon nyt w mielivaltainen funktio ja x = (y, z). Jaetaan yhtälö (A.1) puolittaindw:llä: ( ) ( )dx ∂xdw = dy ∂x∂y dw + dz∂z dw .Jos oletetaan, että z on vakio eli dz = 0, saadaan( ) ( ) ( )∂x ∂x ∂y=∂w ∂y ∂welizz( ) ∂x=∂yzzyz( ) ∂w∂y( )z. (A.6)∂w∂xz