2/1/2013 – CDI-I: Tabela geral de Derivadas
Tabela básica informal com definições, teoremas, dicas, regras de derivação, listagem de conteúdo teórico de derivadas, verifique esclareça suas dúvidas!
Tabela básica informal com definições, teoremas, dicas, regras de derivação, listagem de conteúdo teórico de derivadas, verifique esclareça suas dúvidas!
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
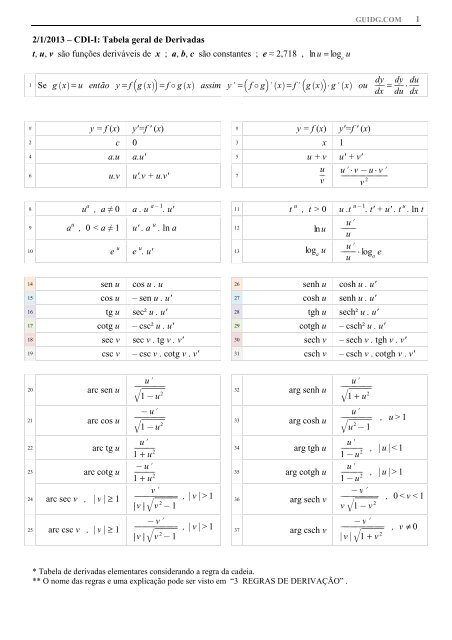
2/1/<strong>2013</strong> <strong>–</strong> <strong>CDI</strong>-I: <strong>Tabela</strong> <strong>geral</strong> <strong>de</strong> <strong>Derivadas</strong><br />
t, u, v são funções <strong>de</strong>riváveis <strong>de</strong> x ; a, b, c são constantes ; e ≈ 2,718 , ln u = log e u<br />
1 Se g x<br />
` a b ` ac<br />
= u então y = f g x<br />
= fN g x<br />
` a b c<br />
assim y. = fN g.<br />
x<br />
` a b ` ac<br />
= f. g x<br />
A g. x<br />
GUIDG.COM 1<br />
` a ou dy<br />
# y = f (x) y'=f ' (x) # y = f (x) y'=f ' (x)<br />
2 c 0 3 x 1<br />
4 a.u a.u' 5 u + v u' + v'<br />
6 u.v u'.v + u.v' 7<br />
uf<br />
v<br />
dx<br />
u.A v@ uA v.<br />
v 2<br />
f = dy<br />
du<br />
8 u a , a ≠ 0 a . u a <strong>–</strong> 1 . u' 11 t u , t > 0 u .t u <strong>–</strong> 1 . t' + u' . t u . ln t<br />
9 a u , 0 < a ≠ 1 u' . a u . ln a 12 ln u<br />
10 e u e u . u' 13 log a u<br />
u. f<br />
u<br />
u. f<br />
A loga e<br />
u<br />
14 sen u cos u . u 26 senh u cosh u . u'<br />
15 cos u <strong>–</strong> sen u . u' 27 cosh u senh u . u'<br />
16 tg u sec² u . u' 28 tgh u sech² u . u'<br />
17 cotg u <strong>–</strong> csc² u . u' 29 cotgh u <strong>–</strong> csch² u . u'<br />
18 sec v sec v . tg v . v' 30 sech v <strong>–</strong> sech v . tgh v . v'<br />
19 csc v <strong>–</strong> csc v . cotg v . v' 31 csch v <strong>–</strong> csch v . cotgh v . v'<br />
20 arc sen u<br />
21 arc cos u<br />
22 arc tg u<br />
23 arc cotg u<br />
24 arc sec v , | v | ≥ 1<br />
25 arc csc v , | v | ≥ 1<br />
u.<br />
1@u 2 q f<br />
w<br />
@ u.<br />
1@u 2 q f<br />
w<br />
u.<br />
32 arg senh u<br />
33 arg cosh u<br />
1 + u 2<br />
f<br />
34 arg tgh u<br />
@ u.<br />
1 + u 2<br />
f<br />
35 arg cotgh u<br />
v.<br />
L<br />
Lv M f<br />
w , | v | > 1<br />
Mq 2 v @ 1<br />
@ v.<br />
L<br />
Lv M f<br />
w , | v | > 1<br />
Mq 2 v @ 1<br />
36 arg sech v<br />
37 arg csch v<br />
* <strong>Tabela</strong> <strong>de</strong> <strong>de</strong>rivadas elementares consi<strong>de</strong>rando a regra da ca<strong>de</strong>ia.<br />
** O nome das regras e uma explicação po<strong>de</strong> ser visto em “3 REGRAS DE DERIVAÇÃO” .<br />
u.<br />
1 + u2 q f<br />
w<br />
f<br />
u.<br />
u2 f<br />
w , u > 1<br />
q @ 1<br />
u.<br />
1@u 2<br />
f<br />
, | u | < 1<br />
u.<br />
1@u 2<br />
f<br />
, | u | > 1<br />
fduf A<br />
dx<br />
@ v.<br />
v 1@ v 2 q f<br />
w , 0 < v < 1<br />
@ v.<br />
| v | 1 + v 2 q f<br />
w , v ≠ 0
Sumário<br />
GUIDG.COM 2<br />
1 CONCEITOS BÁSICOS....................................................................................................................................................3<br />
1.1 Inclinação da reta secante............................................................................................................................................3<br />
1.2 Derivada ......................................................................................................................................................................3<br />
1.3 Notações para a <strong>de</strong>rivada.............................................................................................................................................4<br />
1.4 Equação da reta tangente.............................................................................................................................................4<br />
1.5 Condição <strong>de</strong> paralelismo .............................................................................................................................................5<br />
1.6 Condição <strong>de</strong> perpendicularismo (condição <strong>de</strong> ortogonalida<strong>de</strong>)...................................................................................5<br />
2 DEFINIÇÕES E TEOREMAS ..........................................................................................................................................6<br />
2.1 Continuida<strong>de</strong> da função...............................................................................................................................................6<br />
2.2 Continuida<strong>de</strong> <strong>de</strong> funções <strong>de</strong>riváveis............................................................................................................................6<br />
2.3 <strong>Derivadas</strong> laterais ........................................................................................................................................................6<br />
2.4 Equação da reta normal à curva no ponto ...................................................................................................................7<br />
2.5 Derivada da função inversa .........................................................................................................................................7<br />
3 REGRAS DE DERIVAÇÃO..............................................................................................................................................9<br />
3.1 Derivada da função composta (regra da ca<strong>de</strong>ia)..........................................................................................................9<br />
3.2 Derivada <strong>de</strong> uma constante .........................................................................................................................................9<br />
3.3 Derivada <strong>de</strong> funções polinomiais <strong>de</strong> primeiro grau.....................................................................................................9<br />
3.4 Derivada <strong>de</strong> um produto por uma constante..............................................................................................................10<br />
3.5 Derivada da soma......................................................................................................................................................10<br />
3.6 Derivada do produto..................................................................................................................................................10<br />
3.7 Derivada do quociente...............................................................................................................................................10<br />
3.8 Função exponencial (expoente constante).................................................................................................................10<br />
3.9 Função exponencial (base constante, expoente funcional)........................................................................................10<br />
3.10 Função exponencial (base natural, expoente funcional)............................................................................................10<br />
3.11 Função exponencial composta...................................................................................................................................10<br />
3.12 Função logaritmo natural ..........................................................................................................................................10<br />
3.13 Função logarítmica (base qualquer) ..........................................................................................................................10<br />
3.14 Função seno...............................................................................................................................................................11<br />
3.15 Função co-seno..........................................................................................................................................................11<br />
3.16 Função tangente ........................................................................................................................................................11<br />
3.17 Função co-tangente ...................................................................................................................................................11<br />
3.18 Função secante ..........................................................................................................................................................11<br />
3.19 Função co-secante .....................................................................................................................................................11<br />
3.20 Função arco seno.......................................................................................................................................................12<br />
3.21 Função arco co-seno..................................................................................................................................................12<br />
3.22 Função arco tangente.................................................................................................................................................12<br />
3.23 Função arco co-tangente............................................................................................................................................12<br />
3.24 Função arco secante ..................................................................................................................................................12<br />
3.25 Função arco co-secante .............................................................................................................................................12<br />
3.26 Função seno hiperbólico............................................................................................................................................13<br />
3.27 Função co-seno hiperbólico ......................................................................................................................................13<br />
3.28 Função tangente hiperbólica......................................................................................................................................13<br />
3.29 Função co-tangente hiperbólica.................................................................................................................................13<br />
3.30 Função secante hiperbólica .......................................................................................................................................13<br />
3.31 Função co-secante hiperbólica ..................................................................................................................................13<br />
3.32 Função argumento seno hiperbólico..........................................................................................................................13<br />
3.33 Função argumento co-seno hiperbólico.....................................................................................................................13<br />
3.34 Função argumento tangente hiperbólica....................................................................................................................13<br />
3.35 Função argumento co-tangente hiperbólica...............................................................................................................13<br />
3.36 Função argumento secante hiperbólica .....................................................................................................................13<br />
3.37 Função argumento co-secante hiperbólica ................................................................................................................13<br />
4 REVISÕES DE TEOREMAS E NOTAÇÕES...............................................................................................................14<br />
4.1 <strong>Derivadas</strong> Sucessivas (<strong>de</strong>rivadas <strong>de</strong> or<strong>de</strong>m superior)................................................................................................14<br />
4.2 A <strong>de</strong>rivada num ponto ...............................................................................................................................................14<br />
4.3 Acrécimos (incrementos) ..........................................................................................................................................15<br />
4.4 Diferencial.................................................................................................................................................................15<br />
4.5 Diferenciação sucessiva (diferencial <strong>de</strong> or<strong>de</strong>m superior)..........................................................................................16<br />
4.6 Aproximação linear local ..........................................................................................................................................17<br />
4.7 Taxa <strong>de</strong> variação .......................................................................................................................................................18<br />
5 REFERÊNCIAS BIBLIOGRÁFICAS E LEITURA COMPLEMENTAR .................................................................19
1 CONCEITOS BÁSICOS<br />
GUIDG.COM 3<br />
Um dos problemas ao se estudar a <strong>de</strong>rivada, é que todo o estudo se fundamenta em conceitos <strong>de</strong> limites,<br />
então este conhecimento é necessário. Você po<strong>de</strong> fazer uma breve revisão utilizando a “<strong>Tabela</strong> <strong>de</strong><br />
Limites” e quando houver duvidas quanto aos símbolos use o arquivo “Notação Matemática”. Feito isso,<br />
novos símbolos serão introduzidos, fique atento. Faremos o máximo possível para alertá-lo das diferenças<br />
entre os símbolos que parecem ter o mesmo significado, porém ficam só <strong>de</strong> aparência e na verda<strong>de</strong> são<br />
completamente diferentes. Recomendamos utilizar esta tabela acompanhada <strong>de</strong> um livro para auxilia-lo<br />
nos estudos.<br />
1.1 Inclinação da reta secante<br />
m = tanα = y 2 @ y 1<br />
x 2 @ x 1<br />
f Δyf<br />
=<br />
Δx<br />
Sejam A( x1, y1 ) e B( x2, y2 ) dois pontos quaisquer distintos no plano cartesiano, então o segmento AB<br />
<strong>de</strong>fini uma reta, tal que a inclinação da reta (m) relativa ao eixo x é dado pelo quociente ∆y sobre ∆x .<br />
∆y = y2 − y1<br />
∆x = x2 − x1<br />
Se o segmento AB for paralelo ao eixo y , então não existe m .<br />
* Em diferenciais, entraremos numa nova <strong>de</strong>finição.<br />
1.2 Derivada<br />
A partir <strong>de</strong> 1.1 , admita que os dois pontos A e B fazem parte <strong>de</strong> uma função f (uma curva por<br />
exemplo), então se fizermos B se aproximar a A <strong>de</strong> maneira que a inclinação da reta AB tenda a um<br />
valor limite constante, chamamos este valor <strong>de</strong> inclinação da reta tangente no ponto P ( m p) .<br />
Assim <strong>de</strong>fini-se a <strong>de</strong>rivada quando este limite existe e <strong>de</strong>nota-se por f ' . Portanto geometricamente, a<br />
<strong>de</strong>rivada é a inclinação da reta tangente à curva no ponto P .<br />
lim<br />
ΔxQ 0<br />
` a ` a<br />
f x + Δx @ f x<br />
Δx<br />
Demonstração:<br />
mx 1 = lim<br />
BQ A<br />
Δyf<br />
= lim<br />
Δx x Q x 2 1<br />
mas x 2 = x 1 + Δx<br />
f (I)<br />
y 2 @ y 1<br />
x 2 @ x 1<br />
` a<br />
f f x2@ f x1<br />
=<br />
e se x2Q x1 , ΔxQ 0<br />
b c ` a<br />
f x1 + Δx @ f x1 f<br />
então mx = lim<br />
1 ΔxQ 0 Δx<br />
x 2 @ x 1<br />
` a<br />
f
GUIDG.COM 4<br />
O processo para se encontrar m p (a <strong>de</strong>rivada) é chamado <strong>de</strong>rivação ou diferenciação.<br />
Logo a fórmula (I) é a generalização para um ponto qualquer, <strong>de</strong> uma função qualquer <strong>de</strong>s<strong>de</strong> que<br />
satisfaça os critérios dados.<br />
` a ` a<br />
f x + Δx@<br />
f x f<br />
é por homenagem chamado <strong>de</strong> Quociente <strong>de</strong> Newton.<br />
Δx<br />
* Se8x2 ao D f 9 f. , então dizemos que f é <strong>de</strong>rivável .<br />
* Se m p // ao eixo y então 9+ f. .<br />
* Se m p // ao eixo x então f ' = 0 # se f é constante f. = 0 .<br />
1.3 Notações para a <strong>de</strong>rivada<br />
Veremos agora os símbolos usados para representar a <strong>de</strong>rivada <strong>de</strong> uma função (1.2). Também po<strong>de</strong>mos<br />
encontrar notações extras <strong>de</strong>pen<strong>de</strong>ndo do livro.<br />
dyf<br />
` a<br />
= f. x<br />
dx<br />
I<strong>de</strong>ntificação dos símbolos:<br />
df<br />
dx<br />
Operador <strong>de</strong> <strong>de</strong>rivação: Isto não é um quociente e <strong>de</strong>ve ser visto como um todo. Indica<br />
que o que estiver a sua direita <strong>de</strong>ve ser diferenciado em relação a x (uma variável<br />
qualquer).<br />
dyf<br />
Lê-se: A <strong>de</strong>rivada <strong>de</strong> y em relação à x . Também fala-se dy dx como se escreve.<br />
dx<br />
f. x<br />
` a Lê-se: f linha <strong>de</strong> x . Veja que f. x<br />
` a ≠ f x<br />
` a , Mas f. x<br />
` a = y.<br />
Dx f x<br />
` a Lê-se: A <strong>de</strong>rivada <strong>de</strong> f <strong>de</strong> x “ f (x) ” em relação a x .<br />
Dx y Lê-se: A <strong>de</strong>rivada <strong>de</strong> y em relação a x .<br />
Todas essas notações po<strong>de</strong>m ser aplicadas às regras da tabela <strong>de</strong> <strong>de</strong>rivadas elementares.<br />
1.4 Equação da reta tangente<br />
Com base em 1.1 e 1.2 , po<strong>de</strong>mos <strong>de</strong>finir a equação da reta tangente.<br />
` a<br />
α<br />
` a<br />
y@ y1 = m x@ x1 A fórmula po<strong>de</strong> variar substituindo y1 = f ( x1) em (α) temos:<br />
b c<br />
β<br />
` a ` a<br />
y@f x1 = m x@ x1<br />
α e β são todas equações da reta tangente.
1.5 Condição <strong>de</strong> paralelismo<br />
GUIDG.COM 5<br />
Duas retas r e s são paralelas ( r // s ) quando seus coeficientes angulares (as <strong>de</strong>rivadas) são iguais.<br />
r // s ^ mr = ms<br />
1.6 Condição <strong>de</strong> perpendicularismo (condição <strong>de</strong> ortogonalida<strong>de</strong>)<br />
Duas retas são perpendiculares quando o produto <strong>de</strong> seus coeficientes angulares for igual à um negativo:<br />
r? s ^ mrAms =@ 1<br />
Os exercícios costumam dizer “dada uma reta r normal a s ...”, ou vice e versa. Isto nos diz que as retas<br />
são perpendiculares entre si (formam um ângulo <strong>de</strong> 90º).<br />
*O ângulo <strong>de</strong> 90º é conhecido como o ângulo reto.
2 DEFINIÇÕES E TEOREMAS<br />
GUIDG.COM 6<br />
Nesta seção agrupamos os teoremas mais importantes para uma otimização do estudo <strong>de</strong> <strong>de</strong>rivadas.<br />
2.1 Continuida<strong>de</strong> da função<br />
Uma função é continua num ponto x 1 se aten<strong>de</strong>r simultaneamente a três condições, e são elas:<br />
1 a ` a<br />
9 f x1 2 a ` a<br />
9 lim f x<br />
xQ x1 1<br />
` a ` a<br />
= f x1<br />
3 a lim f x<br />
xQ x1 1<br />
2.2 Continuida<strong>de</strong> <strong>de</strong> funções <strong>de</strong>riváveis<br />
A continuida<strong>de</strong> <strong>de</strong> uma função num ponto não implica na existência da <strong>de</strong>rivada <strong>de</strong>ssa função nesse<br />
mesmo ponto. Porém, toda função <strong>de</strong>rivável num ponto é continua nesse mesmo ponto.<br />
* A <strong>de</strong>monstração foi omitida.<br />
2.3 <strong>Derivadas</strong> laterais<br />
I - Seja a função f <strong>de</strong>finida num ponto a então:<br />
, ` a<br />
f a = lim @ ΔxQ a@ ` a ` a<br />
f a + Δx @ f a<br />
Δx<br />
f<br />
Isto é, a <strong>de</strong>rivada à esquerda <strong>de</strong> f , é o limite para quando ∆x ten<strong>de</strong> à a por valores menores que a .<br />
II - Seja a função f <strong>de</strong>finida num ponto a então:<br />
, ` a<br />
f a = lim<br />
+<br />
ΔxQ a +<br />
` a ` a<br />
f a + Δx @ f a<br />
Δx<br />
f<br />
Isto é, a <strong>de</strong>riva à direita <strong>de</strong> f , é o limite para quando ∆x ten<strong>de</strong> à a por valores maiores que a .<br />
*Se tiver dificulda<strong>de</strong>s, estu<strong>de</strong> primeiro limites laterais.<br />
III - Conclui-se a partir <strong>de</strong> I e II que a <strong>de</strong>rivada <strong>de</strong> uma função num ponto a , existe se, e somente se as<br />
<strong>de</strong>rivadas laterais existirem e forem iguais, isto é:<br />
9 f , , ,<br />
^ f = f@<br />
+<br />
Quando as <strong>de</strong>rivadas laterais existirem, mas forem diferentes, dizemos que este é um ponto anguloso do<br />
gráfico da função. Portanto a <strong>de</strong>rivada <strong>de</strong> f neste caso não existe.<br />
9+ f , , ,<br />
se f ≠ f@<br />
+
2.4 Equação da reta normal à curva no ponto<br />
GUIDG.COM 7<br />
Seja f (x) uma curva contínua e <strong>de</strong>rivável. Logo esta tem n retas tangentes, e portanto n retas normais.<br />
Num ponto <strong>de</strong> uma curva, po<strong>de</strong>-se <strong>de</strong>terminar uma reta normal a esta, <strong>de</strong>s<strong>de</strong> que <strong>de</strong>termine-se<br />
previamente a <strong>de</strong>rivada neste ponto.<br />
2.5 Derivada da função inversa<br />
Nesta seção vamos alerta-lo sobre alguns erros comuns quando a <strong>de</strong>rivada da inversa, e quanto as<br />
notações.<br />
I - A <strong>de</strong>rivada da inversa <strong>de</strong> uma função é igual ao inverso da <strong>de</strong>rivada.<br />
b c<br />
@ 1<br />
f . = 1f<br />
f.<br />
II - Lembre-se f @ 1 ≠ 1f<br />
@ 1<br />
, f é a notação para a inversa da função f , e não o inverso da função f .<br />
f<br />
*Se tiver dúvidas, estu<strong>de</strong> a <strong>de</strong>terminação da inversa <strong>de</strong> uma função (funções inversas).<br />
**Erro comum entre alunos: Se por um instante você acreditar que f @ 1 = 1f<br />
@ 1<br />
e por isso f<br />
então você ainda não enten<strong>de</strong>u.<br />
III <strong>–</strong> Notações para a <strong>de</strong>rivada da inversa.<br />
b c<br />
f<br />
@ 1<br />
. , y<br />
b c<br />
@ 1<br />
. , d<br />
dx<br />
b<br />
f @ 1` ac<br />
f x<br />
IV <strong>–</strong> Formalização do teorema, consi<strong>de</strong>re as seguintes proprieda<strong>de</strong>s relativas à função f :<br />
i ) Seja f uma função <strong>de</strong>finida (contínua) num intervalo (a, b) ;<br />
b c<br />
@ 1<br />
ii ) Suponhamos que f admita inversa f<br />
. Então por ( i ) f @ 1 também é contínua.<br />
f<br />
b c<br />
. = 1f<br />
,<br />
f.<br />
iii ) Se a <strong>de</strong>rivada <strong>de</strong> f existe e é diferente <strong>de</strong> zero para qualquer x pertencente ao intervalo dado, então<br />
a <strong>de</strong>rivada da inversa é igual ao inverso da <strong>de</strong>rivada <strong>de</strong> f .<br />
b c<br />
@ 1<br />
f . = 1f<br />
se, e somente se, i , ii e iii forem satisfeitas.<br />
f.<br />
Em linguagem matemática po<strong>de</strong>mos resumir tudo isso como:<br />
Se9 f x<br />
` a b c<br />
8 x2 a, b<br />
e 9 f. x<br />
` a | f. x<br />
` a b c<br />
≠ 0 8 x2 a, b<br />
b c<br />
@ 1<br />
, então9 f . = 1<br />
f.<br />
b c@ 1<br />
f<br />
= f.<br />
.
Resumindo ainda mais (se fazendo valer i , ii e iii ), dizemos que:<br />
A <strong>de</strong>rivada da inversa é igual ao inverso da <strong>de</strong>rivada.<br />
GUIDG.COM 8<br />
*Este teorema é importante para a <strong>de</strong>finição das <strong>de</strong>rivadas <strong>de</strong> funções trigonométricas inversas, por isso<br />
<strong>de</strong>ve ser compreendido.<br />
** Este teorema foi resumido, no caso <strong>de</strong> obscurida<strong>de</strong> procure a <strong>de</strong>monstração em um dos livros citados<br />
em referências bibliográficas e leitura complementar.
3 REGRAS DE DERIVAÇÃO<br />
GUIDG.COM 9<br />
Agora já po<strong>de</strong>mos seguir para as regras <strong>de</strong> <strong>de</strong>rivação, e serão enunciadas a baixo, on<strong>de</strong> o sinal numérico<br />
# indica a or<strong>de</strong>m na tabela <strong>geral</strong> <strong>de</strong> <strong>de</strong>rivadas elementares que po<strong>de</strong> ser vista na primeira página.<br />
As regras <strong>de</strong> <strong>de</strong>rivação existem com o único objetivo <strong>de</strong> tornar o método <strong>de</strong> diferenciação mais eficiente,<br />
visto que o uso da <strong>de</strong>finição é extenso e <strong>de</strong>snecessário para os próximos casos.<br />
3.1 Derivada da função composta (regra da ca<strong>de</strong>ia)<br />
Se y = f u<br />
` a e u = g x<br />
` a b ` ac<br />
são funções <strong>de</strong>riváveis, e f g x = fN g x<br />
` a está <strong>de</strong>finida, então a <strong>de</strong>rivada<br />
<strong>de</strong> fN g x<br />
` a é dada por:<br />
b c<br />
fN g.<br />
x<br />
` a b ` ac<br />
= f. g x<br />
` a<br />
A g. x<br />
Aplicando a notação <strong>de</strong>finida em 1.3 temos:<br />
dy<br />
dx<br />
f = dy<br />
du<br />
fduf A<br />
dx<br />
Exemplo: Derive a função y = ln x 2 b c<br />
+ 1 :<br />
Solução: Para este exemplo precisamos conhecer primeiramente a <strong>de</strong>rivada da função logaritmo natural.<br />
Fazendo u = x 2 + 1 , temos y = ln u<br />
` a , então:<br />
y. = dy<br />
du<br />
f = 1<br />
u<br />
Aplicando a regra dy<br />
dx<br />
dy<br />
dx<br />
f = 1<br />
u<br />
f duf<br />
, u. = = 2x<br />
dx<br />
f A 2x = 2x<br />
u<br />
f = dy<br />
du<br />
fduf A temos:<br />
dx<br />
f 2 dyf<br />
2x<br />
, como u = x + 1 , então =<br />
dx x 2 f<br />
A<br />
+ 1<br />
* Não precisamos dar nomes as funções como fizemos, a importância da regra é quanto a ca<strong>de</strong>ia, ou seja,<br />
quando tratamos <strong>de</strong> funções compostas: a <strong>de</strong>rivação começa com a aplicação das regras externamente em<br />
direção as funções internas, e por isso o nome. A <strong>de</strong>monstração foi omitida.<br />
3.2 Derivada <strong>de</strong> uma constante<br />
A <strong>de</strong>rivada da função constante é zero por que a reta tangente à curva é paralela ao eixo x , logo não<br />
existe inclinação, e se a <strong>de</strong>rivada é a inclinação, então não existe a <strong>de</strong>rivada.<br />
3.3 Derivada <strong>de</strong> funções polinomiais <strong>de</strong> primeiro grau<br />
A <strong>de</strong>rivada <strong>de</strong> uma variável in<strong>de</strong>pen<strong>de</strong>nte qualquer com expoente um, é um.<br />
Exemplo: Se x , y , z são variáveis in<strong>de</strong>pen<strong>de</strong>ntes então suas <strong>de</strong>rivadas são um, respectivamente.<br />
A prova <strong>de</strong>sta regra é obtida <strong>de</strong>rivando-se pela <strong>de</strong>finição a função f (x) = x .
3.4 Derivada <strong>de</strong> um produto por uma constante<br />
Por aplicação <strong>de</strong> proprieda<strong>de</strong> <strong>de</strong> limites po<strong>de</strong>mos enunciar:<br />
A <strong>de</strong>rivada <strong>de</strong> um produto <strong>de</strong> f(x) por uma constante, é a constante vezes a <strong>de</strong>rivada <strong>de</strong> f(x).<br />
A prova <strong>de</strong>sta regra é obtida <strong>de</strong>rivando-se pela <strong>de</strong>finição a função f (x) = c.x .<br />
3.5 Derivada da soma<br />
A <strong>de</strong>rivada da soma é a soma das <strong>de</strong>rivadas.<br />
*Demonstração em breve.<br />
3.6 Derivada do produto<br />
*Demonstração em breve.<br />
3.7 Derivada do quociente<br />
*Demonstração em breve.<br />
3.8 Função exponencial (expoente constante)<br />
*Demonstração em breve.<br />
3.9 Função exponencial (base constante, expoente funcional)<br />
*Demonstração em breve.<br />
3.10 Função exponencial (base natural, expoente funcional)<br />
*Demonstração em breve.<br />
3.11 Função exponencial composta<br />
*Demonstração em breve.<br />
3.12 Função logaritmo natural<br />
Derivada da função logaritmo natural ou logaritmo <strong>de</strong> base e, ou também logaritmo neperiano.<br />
3.13 Função logarítmica (base qualquer)<br />
*Demonstração em breve.<br />
GUIDG.COM 10
3.14 Função seno<br />
GUIDG.COM 11<br />
A regra #13 diz que para y = sin u implica que y’ = u´cos u , levando em consi<strong>de</strong>ração a regra da<br />
ca<strong>de</strong>ia (3.1).<br />
Demonstração: Se y = sin u , então aplicando a <strong>de</strong>finição temos:<br />
y. = lim<br />
ΔxQ 0<br />
mas: sin x + Δx<br />
y. = lim<br />
ΔxQ 0<br />
y. = lim<br />
ΔxQ 0<br />
` a<br />
f x + Δx @ f x<br />
Δx<br />
` a<br />
` a<br />
f sin x + Δx @ sin x<br />
=<br />
Δx<br />
` a = sinxA cosΔx + sinΔxAcos x<br />
sinxA cosΔx + sinΔxA cos x@ sin xf<br />
Δx<br />
` a<br />
sinx cosΔx@ 1A<br />
+ sinΔxAcos x<br />
Δx<br />
` a<br />
S y. = lim sin xA lim<br />
ΔxQ 0 ΔxQ 0<br />
y. = sin xA0 + 1A cos<br />
# y. = cos x<br />
f<br />
cosΔx@ 1f<br />
+ lim<br />
Δx ΔxQ 0<br />
` a<br />
f<br />
sinΔxf<br />
A lim cos x<br />
Δx ΔxQ 0<br />
(S) Simplificação: Para este ponto em diante utilizou-se as proprieda<strong>de</strong>s <strong>de</strong> limites junto com a aplicação<br />
<strong>de</strong> limites fundamentais.<br />
3.15 Função co-seno<br />
*Demonstração em breve.<br />
3.16 Função tangente<br />
*Demonstração em breve.<br />
3.17 Função co-tangente<br />
*Demonstração em breve.<br />
3.18 Função secante<br />
*Demonstração em breve.<br />
3.19 Função co-secante<br />
*Demonstração em breve.
3.20 Função arco seno<br />
A função f(x) = arc sin x é <strong>de</strong>finida no intervalo D: [-1 , 1] em IM: [-π/2 , π/2] .<br />
1 f<br />
Então y = f(x) é <strong>de</strong>rivável em (-1 , 1) e y. = .<br />
q w<br />
1@x 2<br />
A <strong>de</strong>monstração é trivial, por aplicação do teorema da inversa (2.5) :<br />
Se y = arcsin x então:<br />
` a<br />
α x = sin y , procuramos pela <strong>de</strong>rivada da inversa, então por T5:<br />
b c<br />
@ 1 x<br />
. =<br />
1<br />
b c<br />
siny<br />
sin 2 y + cos 2 y = 1<br />
.<br />
b c<br />
f<br />
[ β<br />
cos 2 y = 1@sin 2 y [ γ<br />
por α<br />
substituindo em γ<br />
b c<br />
@ 1 x . = 1 f<br />
cos y<br />
w<br />
` a 2<br />
cos y = q1@sin y<br />
` a temos: x = siny [ x 2 = sin 2 y<br />
cos y = 1@ x 2 q w<br />
` a :<br />
b c<br />
substituindo em β<br />
b c<br />
@ 1 x<br />
. = y. =<br />
1<br />
:<br />
q f<br />
w<br />
1@x 2<br />
* Neste caso x@ 1 ≠ 1f<br />
@ 1 , x e está indicando a inversa da funçãoA<br />
x<br />
3.21 Função arco co-seno<br />
*Demonstração em breve.<br />
3.22 Função arco tangente<br />
*Demonstração em breve.<br />
3.23 Função arco co-tangente<br />
*Demonstração em breve.<br />
3.24 Função arco secante<br />
*Demonstração em breve.<br />
3.25 Função arco co-secante<br />
*Demonstração em breve.<br />
GUIDG.COM 12
3.26 Função seno hiperbólico<br />
GUIDG.COM 13<br />
*As <strong>de</strong>rivadas das funções hiperbólicas, são as <strong>de</strong>rivadas <strong>de</strong> suas respectivas funções exponenciais.<br />
3.27 Função co-seno hiperbólico<br />
*Demonstração em breve.<br />
3.28 Função tangente hiperbólica<br />
*Demonstração em breve.<br />
3.29 Função co-tangente hiperbólica<br />
*Demonstração em breve.<br />
3.30 Função secante hiperbólica<br />
*Demonstração em breve.<br />
3.31 Função co-secante hiperbólica<br />
*Demonstração em breve.<br />
3.32 Função argumento seno hiperbólico<br />
*As <strong>de</strong>rivadas das funções hiperbólicas inversas, são as <strong>de</strong>rivadas dos argumentos das funções<br />
hiperbólicas.<br />
3.33 Função argumento co-seno hiperbólico<br />
*Demonstração em breve.<br />
3.34 Função argumento tangente hiperbólica<br />
*Demonstração em breve.<br />
3.35 Função argumento co-tangente hiperbólica<br />
*Demonstração em breve.<br />
3.36 Função argumento secante hiperbólica<br />
*Demonstração em breve.<br />
3.37 Função argumento co-secante hiperbólica<br />
*Demonstração em breve.
4 REVISÕES DE TEOREMAS E NOTAÇÕES<br />
GUIDG.COM 14<br />
Nesta seção agrupamos mais alguns teoremas com observações importantes para a uma otimização do<br />
estudo <strong>de</strong> <strong>de</strong>rivadas.<br />
4.1 <strong>Derivadas</strong> Sucessivas (<strong>de</strong>rivadas <strong>de</strong> or<strong>de</strong>m superior)<br />
Seja f uma função <strong>de</strong>rivável, e se a própria <strong>de</strong>rivada <strong>de</strong> f for <strong>de</strong>rivável, então chamamos esta <strong>de</strong><br />
<strong>de</strong>rivada segunda. Se a <strong>de</strong>rivada segunda for <strong>de</strong>rivável, esta se chamará <strong>de</strong>rivada terceira, e assim<br />
sucessivamente.<br />
Notações extras:<br />
y. = f. x<br />
` a [ dyf<br />
d<br />
=<br />
dx dx<br />
y. = f. x<br />
y/ = f/ x<br />
(<br />
` a [ d2 y<br />
dx 2<br />
` a [ d3 y<br />
dx 3<br />
b<br />
f ` ac<br />
f x<br />
f b ` acg<br />
f df<br />
df<br />
= f x<br />
dx dx<br />
f d<br />
=<br />
dx<br />
h<br />
f d 2<br />
j<br />
dx 2<br />
i<br />
b c<br />
f ` a<br />
f x<br />
Em <strong>geral</strong> isto po<strong>de</strong> ser resumido como:<br />
y n<br />
` a<br />
= f n<br />
` a`<br />
a d<br />
x [ n y<br />
dx n<br />
f d<br />
= n<br />
dx n<br />
b<br />
f ` ac<br />
f x<br />
= d2<br />
dx 2<br />
k= d3<br />
dx 3<br />
b<br />
f ` ac<br />
f x<br />
b<br />
f ` ac<br />
f x<br />
Lê-se: A <strong>de</strong>rivada n-ésima <strong>de</strong> y = a <strong>de</strong>rivada n-ésima <strong>de</strong> f (x).<br />
Por razões <strong>de</strong> interpretação, para n > III' , utiliza-se números naturais <strong>de</strong>ntro <strong>de</strong> parênteses:<br />
f. , f. , f/ , f 4<br />
` a<br />
, f 5<br />
` a<br />
, f 6<br />
` a<br />
4.2 A <strong>de</strong>rivada num ponto<br />
, f 7<br />
` a<br />
, f n<br />
` a<br />
…<br />
A seguir veremos a notação para a <strong>de</strong>rivada <strong>de</strong> uma função num ponto, a partir da notação <strong>de</strong> Leibniz.<br />
Neste caso k sendo uma constante, que seria substituída na variável x da função y já <strong>de</strong>rivada. Assim<br />
obtendo o valor da <strong>de</strong>rivada neste ponto.<br />
Esta notação é uma variação da notação convencional, isto é:<br />
ou<br />
= y. x<br />
` a = f. x<br />
` a para x = k<br />
Isto será muito aplicado na <strong>de</strong>rivada na forma paramétrica, na forma implícita e principalmente na taxa <strong>de</strong><br />
variação e taxas relacionadas, com o intuito <strong>de</strong> aliviar a notação.
4.3 Acrécimos (incrementos)<br />
GUIDG.COM 15<br />
Seja f (x) uma função, então sempre po<strong>de</strong>mos consi<strong>de</strong>rar uma variação <strong>de</strong> x . Se fizermos x variar <strong>de</strong><br />
x1 até x2 , <strong>de</strong>finimos o acrécimo <strong>de</strong> x e <strong>de</strong>notamos por ∆x.<br />
Δx = x 2 @ x 1<br />
A variação <strong>de</strong> x origina uma correspon<strong>de</strong>nte variação <strong>de</strong> y , <strong>de</strong>notada por:<br />
` a ` a<br />
Δy = y2@ y1 = f x2@ f x1<br />
Mas x 2 = x 1 + Δx , então substituindo em ∆y:<br />
b c ` a<br />
Δy = f x1 + Δx @ f x1 4.4 Diferencial<br />
Com base em 4.3 , entraremos na <strong>de</strong>finição <strong>de</strong> diferencial.<br />
Seja y = f (x) uma função <strong>de</strong>rivável, e ∆x um acrécimo <strong>de</strong> x , então:<br />
I) A diferencial <strong>de</strong> x (variável in<strong>de</strong>pen<strong>de</strong>nte), <strong>de</strong>nota-se dx = Δx<br />
II) Já a diferencial <strong>de</strong> y é <strong>de</strong>pen<strong>de</strong>nte, é só existe <strong>de</strong>vido a <strong>de</strong>rivada, <strong>de</strong>nota-se:<br />
dy = f. x<br />
` a A Δx ou dy = f. x<br />
` a A dx<br />
III) Então com base em 1.2 e 1.3 , re-<strong>de</strong>fimos a <strong>de</strong>rivada como o quociente entre duas diferenciais:<br />
dy<br />
Δx<br />
f dyf<br />
` a<br />
= = f. x<br />
dx<br />
4.4.1 Os significados geométricos<br />
O acrécimo dx = Δx , ocorre no eixo das abscissas (eixo x ).<br />
dy ≠ Δy mas dy ≈ Δy se ∆x for consi<strong>de</strong>rado um valor pequeno.<br />
O acrécimo Δy , ocorre no eixo das or<strong>de</strong>nadas (eixo y);<br />
Mas o acrécimo dy é um produto, e ocorre <strong>de</strong>vido a variação da reta tangente (isto é <strong>de</strong> sua inclinação).<br />
É importante lembrar que Δy<br />
f g<br />
f Δyf<br />
dyf<br />
não é a <strong>de</strong>rivada em si ≠ . Mas po<strong>de</strong> ser interpretado<br />
Δx<br />
Δx dx<br />
geometricamente como a inclinação da reta secante <strong>de</strong>finida pelos dois pontos.
4.4.2 Derivada, re-<strong>de</strong>finição<br />
GUIDG.COM 16<br />
Em 1.1 fizemos uma observação que a <strong>de</strong>rivada seria re<strong>de</strong>finida quando chegássemos em diferenciais, e<br />
agora estamos aptos para esta re-<strong>de</strong>finição (que não tem tantas mudanças, apenas na interpretação):<br />
dyf<br />
Δyf<br />
= lim = lim<br />
dx ΔxQ 0 Δx ΔxQ 0<br />
b c<br />
f x1 + Δx @ f x1 Δx<br />
` a<br />
f<br />
Portanto a <strong>de</strong>rivada é o limite do quociente ∆y / ∆x , quando ∆x ten<strong>de</strong> a zero.<br />
4.5 Diferenciação sucessiva (diferencial <strong>de</strong> or<strong>de</strong>m superior)<br />
Com base em 4.4 <strong>–</strong> II , seja y = f x<br />
` a temos que dy = f. x<br />
` a A dx , então se a diferencial da função y for<br />
diferenciável, temos d 2 y = f. x<br />
` a A dx 2 e esta se chamará a diferencial segunda, se novamente for<br />
diferenciável teremos a diferencial terceira dada por d 3 y = f/ x<br />
` a A dx 3 , e assim sucessivamente.<br />
A diferencial n-ésima <strong>de</strong> y é dada por: d n y = f n<br />
` a`<br />
a n<br />
xA<br />
dx .<br />
Veja que isso esta baseado na manipulação algébrica da <strong>de</strong>rivada <strong>de</strong> or<strong>de</strong>m superior, isto é, para a função<br />
y = f x<br />
` a , seja # a or<strong>de</strong>m da operação, temos:<br />
# As <strong>de</strong>rivadas sucessivas: As diferenciais sucessivas:<br />
1<br />
dyf<br />
` a<br />
= f. x<br />
dx<br />
dy = f. x<br />
` a A dx<br />
2<br />
d 2 y<br />
3<br />
dx 2<br />
d 3 y<br />
dx 3<br />
f ` a 2 ` a 2<br />
= f. x<br />
d y = f. xA<br />
dx<br />
f ` a 3 ` a 3<br />
= f/ x<br />
d y = f/ xA<br />
dx<br />
... ... ...<br />
n<br />
d n y<br />
dx n<br />
` a<br />
f n`<br />
a<br />
= f x<br />
n n<br />
d y = f<br />
` a`<br />
a n<br />
A dx<br />
x
4.6 Aproximação linear local<br />
GUIDG.COM 17<br />
A partir <strong>de</strong> 1.4 , <strong>de</strong>finimos a aproximação linear local. Intuitivamente esta é uma ferramenta que nos dará<br />
a partir <strong>de</strong> dados conhecidos, valores próximos a estes. Para uso por exemplo na resolução <strong>de</strong> problemas<br />
3q como: 65,5<br />
w ` a<br />
, tan 45º4. 30. , etc.<br />
b c ` a ` a<br />
f x1 + Δx ≈ f. x1A Δx + f x1<br />
Demonstração: Partindo <strong>de</strong> 1.4 (a equação da reta tangente), saímos <strong>de</strong> α e seguimos:<br />
` a<br />
α<br />
b c<br />
β<br />
` a<br />
y@ y1 = m x@ x1 ` a ` a<br />
y@ f x1 = m x@ x1<br />
` a ` a<br />
mas: x@ x1 = Δx , y = f x e m = f. x1 ` a<br />
então: γ f x<br />
` a ` a ` a<br />
@ f x1 = f. x1A<br />
Δx<br />
` a<br />
logo: δ f x<br />
` a ` a ` a<br />
= f. x1A Δx + f x1<br />
novamente: x@ x1 = Δx [ x = x1 + Δx<br />
Agora substituindo em δ chegamos exatamente aon<strong>de</strong> queremos, ou seja:<br />
` a<br />
ε<br />
b c ` a ` a<br />
f x1 + Δx ≈ f. x1A Δx + f x1<br />
` a<br />
Veja que o sinal <strong>de</strong> igualda<strong>de</strong> muda, por estarmos tratando <strong>de</strong> uma aproximação, por que y = f x<br />
somente para valores próximos <strong>de</strong> x1 , e é a melhor medida que po<strong>de</strong>mos obter a partir <strong>de</strong> x1 .<br />
A interpretação <strong>de</strong> ε : Po<strong>de</strong>mos interpretar a aproximação linear local da seguinte maneira, dado um<br />
valor conhecido x 1 , então se estivermos buscando por um valor x próximo <strong>de</strong> x 1 , isto é x = x 1 + Δx ,<br />
então po<strong>de</strong>mos utilizar (ε) a aproximação linear local para <strong>de</strong>termina-lo, visto que temos x 1 e a<br />
aproximação Δx .
4.7 Taxa <strong>de</strong> variação<br />
GUIDG.COM 18<br />
Toda <strong>de</strong>rivada po<strong>de</strong> ser interpretada como uma taxa <strong>de</strong> variação. Dada uma função y = f(x) , quando a<br />
variável in<strong>de</strong>pen<strong>de</strong>nte varia <strong>de</strong> x à x + ∆x , existe uma correspon<strong>de</strong>nte variação <strong>de</strong> y dada por<br />
∆y = f (x + ∆x) <strong>–</strong> f (x) . ∆y que <strong>de</strong>finimos em 1.1 e por equivalência chegou a esta última forma.<br />
Com isto <strong>de</strong>finimos genericamente:<br />
I - Taxa <strong>de</strong> variação média:<br />
Δy<br />
` a ` a<br />
f f x + Δx @ f x f<br />
=<br />
Δx Δx<br />
* Interpretação informal:<br />
Δy<br />
Δx<br />
f = variação <strong>de</strong> y<br />
variação <strong>de</strong> x<br />
f y final@ yinicialf =<br />
x final@ xinicial Isto é, com esse quociente po<strong>de</strong>mos <strong>de</strong>finir a média da variação <strong>de</strong> alguma coisa em relação à outra<br />
variação, in<strong>de</strong>pen<strong>de</strong>nte do que seja. Veja a interpretação mecânica.<br />
II - Taxa <strong>de</strong> variação instantânea ou simplesmente Taxa <strong>de</strong> Variação, que é a própria <strong>de</strong>rivada:<br />
f. x<br />
` a = lim<br />
ΔxQ 0<br />
Δyf<br />
= lim<br />
Δx ΔxQ 0<br />
` a ` a<br />
f x + Δx @ f x<br />
Δx<br />
4.7.1 Interpretação mecânica e nomes especiais<br />
f<br />
I - Velocida<strong>de</strong> média: Po<strong>de</strong>mos <strong>de</strong>finir com um exemplo prático. Se a distância <strong>de</strong> um ponto A até<br />
outro B é 80Km , e uma partícula viajou <strong>de</strong> A para B , em uma hora, então sua velocida<strong>de</strong> média é<br />
80Km/h (lê-se quilômetros por hora), mesmo que durante o percurso ela tenha acelerado ou freado.<br />
II - Velocida<strong>de</strong> instantânea: Esta po<strong>de</strong> ser vista no painel <strong>de</strong> um automóvel em movimento, que<br />
significa é a taxa <strong>de</strong> variação do espaço em relação ao tempo (este medido num intervalo muito curto, por<br />
isso emprega-se o limite da função para ∆x ten<strong>de</strong>ndo a zero, ∆x é a variação do tempo.<br />
III - Aceleração: é a taxa <strong>de</strong> variação da velocida<strong>de</strong> em relação ao tempo.<br />
IV - Densida<strong>de</strong> Linear: Em fios elétricos, por exemplo, é a taxa <strong>de</strong> variação da massa em relação ao<br />
comprimento do fio.<br />
V - Vazão: Em uma torneira, por exemplo, é a taxa <strong>de</strong> variação do volume <strong>de</strong> água <strong>de</strong>spejado em relação<br />
ao tempo.<br />
A aplicação se esten<strong>de</strong> em diversas áreas.
5 REFERÊNCIAS BIBLIOGRÁFICAS E LEITURA COMPLEMENTAR<br />
(1) Diva Marilia Flemming - Cálculo A (5ª edição) ;<br />
(2) Paulo Boulos - Cálculo diferencial e integral Vol.1 ;<br />
(3) Louis Leithold <strong>–</strong> O cálculo com geometria analítica Vol.1 ;<br />
(4) W.A. Granville <strong>–</strong> Elementos <strong>de</strong> Cálculo Diferencial e Integral ;<br />
GUIDG.COM 19<br />
(5) Apostila <strong>de</strong> Cálculo Diferencial e Integral 2010/1 <strong>–</strong> Departamento <strong>de</strong> Matemática (UDESC <strong>–</strong> CCT)