Όρια και Î£Ï Î½Î­Ï‡ÎµÎ¹Î±

1
Κεφάλαιο 5
Όριο και συνέχεια συνάρτησης
5.1 Όριο συνάρτησης για x→x 0 єR
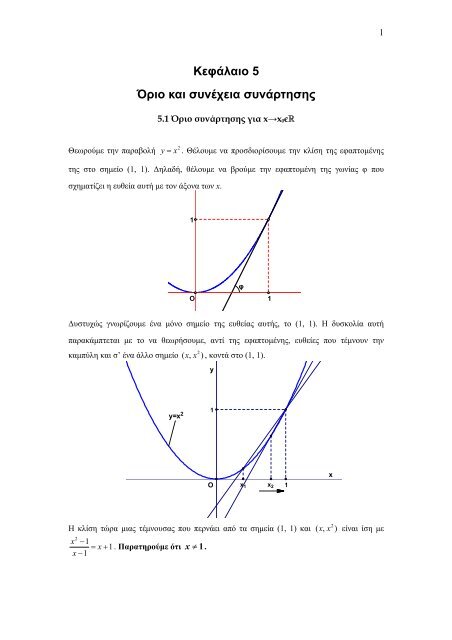
Θεωρούµε την παραβολή
y
2
= x . Θέλουµε να προσδιορίσουµε την κλίση της εφαπτοµένης
της στο σηµείο (1, 1). ∆ηλαδή, θέλουµε να βρούµε την εφαπτοµένη της γωνίας φ που
σχηµατίζει η ευθεία αυτή µε τον άξονα των x.
1
φ
O 1
∆υστυχώς γνωρίζουµε ένα µόνο σηµείο της ευθείας αυτής, το (1, 1). Η δυσκολία αυτή
παρακάµπτεται µε το να θεωρήσουµε, αντί της εφαπτοµένης, ευθείες που τέµνουν την
καµπύλη και σ’ ένα άλλο σηµείο
2
( x, x ), κοντά στο (1, 1).
y
y=x 2 1
O
x 1 x 2
1
x
Η κλίση τώρα µιας τέµνουσας που περνάει από τα σηµεία (1, 1) και
2
x − 1 = x + 1 . Παρατηρούµε ότι x ≠ 1.
x −1
2
( x, x ) είναι ίση µε

2
∆ίνοντας στο x διαδοχικές τιµές x1, x
2,
…, ολοένα πιο κοντά στο 1, παρατηρούµε ότι η
τέµνουσα ευθεία πλησιάζει όλο και περισσότερο τη θέση της εφαπτοµένης και η τιµή του
κλάσµατος πλησιάζει στην τιµή 1+ 1= 2. Εποµένως η κλίση της εφαπτοµένης ευθείας πρέπει
να είναι ίση µε 2. Γράφουµε
2
x −1
tan φ = lim = 2 .
x→1
x −1
Τώρα είµαστε σε θέση να προσδιορίσουµε την εξίσωση της εφαπτόµενης ευθείας (εφόσον
γνωρίζουµε ότι περνά από το σηµείο (1, 1) και ότι η κλίση της είναι 2). Η εξίσωση είναι:
y− 1= 2 ⋅( x−1) ⇔ y = 2x−1
Προβλήµατα όπως το προηγούµενο µας οδηγούν στην έννοια του ορίου µιας συνάρτησης.
Αλλά, ας ξεκαθαρίσουµε πρώτα ένα λεπτό σηµείο: Το σηµείο στο οποίο τείνει η µεταβλητή x
πρέπει να «γειτονεύει», όσο κοντά θέλουµε, µε σηµεία του πεδίου ορισµού της συνάρτησης.
Έτσι, αποκτά έννοια ο συµβολισµός x → x0
.
Συνήθως το πεδίο ορισµού της συνάρτησης περιέχει ένα σύνολο της µορφής ( x0 − δ , x0)
ή
( x0, x0
+ δ ) ή ( x0 − δ , x0) ∪ ( x0, x0
+ δ ), όπου δ > 0 , οπότε το x
0
βρίσκεται όσο κοντά
θέλουµε σε σηµεία του πεδίου ορισµού.
Απαιτούµε δηλαδή, για οποιαδήποτε δ > 0 , να υπάρχει κάποιο σηµείο του πεδίου ορισµού Α
που ανήκει στο σύνολο ( x0 −δ
, x0) ∪ ( x0, x0
+ δ ), δηλαδή «κοντά» στο x
0
(και που δεν είναι
το x
0
).
5.1.1 Ορισµός
Έστω A ⊆ R . Ένας αριθµός x
0
λέγεται σηµείο συσσωρεύσεως του Α αν, για κάθε δ > 0 , το
σύνολο (( x0 −δ
, x0) ∪ ( x0, x0
+ δ )) ∩ A είναι µη κενό.
δ 1
x 4
δ 2
x 0
δ 3
δ 4
x 1
x 3 x 2
*[Η ιδιότητα αυτή του σηµείου συσσωρεύσεως έχει ως αποτέλεσµα να συσσωρεύονται σε
κάθε περιοχή ( x0 − δ , x0
+ δ ) του σηµείου x
0
άπειρα σηµεία του Α.

3
άπειρα σηµεία του Α
x 0 -δ
x 0
+δ
x 0
Η εισαγωγή του παραπάνω, µάλλον γενικού ορισµού, έγινε για να αντιµετωπιστούν όλες οι
επιµέρους περιπτώσεις κατά ενιαίο τρόπο.]
Σε αντιστοιχία µε τον εψιλοντικό ορισµό του ορίου για τις ακολουθίες έχουµε:
5.1.2 Ορισµός
Θεωρούµε τη συνάρτηση f : A→ R . Αν x
0
είναι σηµείο συσσωρεύσεως του Α, τότε λέµε ότι η
συνάρτηση f συγκλίνει για x → x0
στον πραγµατικό αριθµό a αν, για κάθε ε > 0 (οσοδήποτε
µικρό) υπάρχει δ > 0 µε την ιδιότητα:
Αν x∈ A και x∈( x0 −δ
, x0) ∪ ( x0, x0
+ δ ) τότε | f( x) − a|
< ε .
Ο αριθµός a λέγεται όριο της f για x → x0
.
y
y = f(x)
2ε
a
Ο
2δ
x 0
x
5.1.3 Παρατήρηση
(i) Η σχέση x∈( x0 −δ
, x0) ∪ ( x0, x0
+ δ ) είναι ισοδύναµη µε την αλγεβρική σχέση
0 < | x− x | < δ .
0
(ii) Το x στον ορισµό του ορίου δεν είναι ποτέ ίσο µε x
0
, γιατί σε µια τέτοια περίπτωση θα
µπορούσε να µην έχει έννοια η ποσότητα f ( x ). (∆είτε το προηγούµενο παράδειγµα, όπου
x ≠ 1). Γι’ αυτό και απαιτούµε 0 < | x − x0
| . Όπως µάλιστα θα δούµε στη συνέχεια, η

4
συνάρτηση µε τύπο
sin x
y = συγκλίνει στο 1, για x → 0 και φυσικά, το 0 δεν ανήκει στο
x
πεδίο ορισµού της.
Όπως και στις ακολουθίες, έτσι και δω, το όριο µιας συνάρτησης για x → x0
, είναι µοναδικό.
5.1.4 Πρόταση
Θεωρούµε τη συνάρτηση f : A→ R . Έστω x
0
σηµείο συσσωρεύσεως του Α. Αν η f συγκλίνει
(για x → x0
) ταυτόχρονα στους αριθµούς a
1
και a
2
, τότε a1 = a2.
*Απόδειξη: Έστω ότι a1 ≠ a2. Μπορούµε να υποθέσουµε ότι a1 < a2. Τότε, για
a2 − a1 ε = > 0 , υπάρχουν θετικοί αριθµοί δ
1
και δ
2
, τέτοιοι ώστε για κάθε x∈ A µε
2
0 | |
< x− x0 < δ1
και 0 | x x0 | δ2
< − < , να ισχύουν ταυτόχρονα οι σχέσεις | f( x) − a1
| < ε και
| f( x) − a2
| < ε . Άρα, αν δ = min{ δ1, δ2} > 0 , θα έχουµε:
x∈ A και 0 < | x− x0 | < δ ⇒| f( x) − a1| < ε και | f( x) − a2
| < ε ⇒
⇒ 2 ε = | a −a | ≤| f( x) − a | + | f( x) − a | < ε + ε = 2 ε,
δηλαδή 2ε
< 2ε
, άτοπο. ■
1 2 1 2
Το µοναδικό αυτό όριο της συνάρτησης f (για x → x0
) συµβολίζεται µε
lim f ( x ) .
x→x
0
Η επόµενη πρόταση αναφέρεται στη διάταξη των ορίων.
5.1.5 Πρόταση
Θεωρούµε συναρτήσεις f και g µε κοινό πεδίο ορισµού Α. Έστω x
0
σηµείο συσσώρευσης του Α.
(i) Αν f( x) ≥ 0 για κάθε σηµείο x του Α που ανήκει σε µια γειτονιά ( x0 − δ , x0) ∪ ( x0, x0
+ δ )
του x
0
, τότε lim f( x) ≥ 0 .
x→x0
(ii) Αν f ( x) ≥ g( x)
για κάθε σηµείο x του Α που ανήκει σε µια γειτονιά
( x0 −δ
, x0) ∪ ( x0, x0
+ δ ) του x
0
, τότε lim f ( x) ≥ lim g( x)
.
*Απόδειξη: Αποδεικνύουµε αρχικά το (i).
x→x0 x→x0
Θέτουµε a= lim f( x)
. Υποθέτουµε ότι a < 0 . Τότε, για
x→x0
ε =− a > 0 , θα υπάρχει δ ′ > 0 µε την ιδιότητα: Για κάθε
x∈ A µε 0 < | x− x0
| < δ ′ ισχύει | f ( x) − a|

5
δ ′′ = min{ δδ , ′} > 0 , τότε θα ισχύουν ταυτόχρονα οι
σχέσεις: f( x) ≥ 0 και | f ( x) − a| 0. Από τον ορισµό του ορίου
προκύπτει ότι υπάρχει δ > 0 µε την ιδιότητα: Για κάθε x∈ A , µε 0 < | x− x0
| < δ , ισχύει
| f( x) − a| < ε ′ = ε /| λ|
, απ’ όπου, | λ f( x) − λa|
< ε .
Για το (v) εφαρµόζουµε το (γνωστό από τις ακολουθίες) τέχνασµα του ε /2. Για ε > 0 ,
υπάρχουν δ
1
> 0 και δ
2
> 0 µε τις ιδιότητες: Για κάθε x∈ A , µε 0 < | x− x0 | < δ1, και
x→x0

6
0 < | x− x0 | < δ2
(συνοπτικότερα, x∈ A , µε 0 < | x− x0
| < δ , όπου δ = min{ δ1, δ2} > 0 )
ισχύουν οι σχέσεις:
| f( x) − a| < ε /2 και | gx ( ) − b| < ε /2.
Από την τριγωνική ανισότητα προκύπτει: | f ( x) + g( x) − ( a+ b) | = | ( f( x) − a)
+ ( g( x) −b)|
≤
| f( x) − a| + | g( x) − b| < ε /2 + ε /2= ε .
Για το
lim( f ( x) − g( x))
παρατηρούµε ότι
x→x0
x→x0 x→x0
x→x0 x→x0
lim( f( x) − g( x)) = lim( f( x) + ( − g( x)))
=
x→x0 x→x0
= lim f ( x) + lim( − g( x))
και, από (iv), lim( − gx ( )) =− lim gx ( ).
*[Για το (vi) παρατηρούµε ότι | f ( xgx ) ( ) − ab| = | f( xgx ) ( ) − f( xb ) + f( xb ) − ab || ≤ f ()| x
| g( x) − b| + | b|| f( x) − a|
.
Έστω ε > 0. Θεωρούµε έναν άλλο θετικό αριθµό ε ′ , που εξαρτάται από τον ε και τον οποίο
θα προσδιορίσουµε στη συνέχεια.
Εφόσον lim f ( x)
= a και lim gx ( ) = b , υπάρχει δ > 0 µε την ιδιότητα: Για κάθε x∈ A , µε
x x
x→x0
0
→ 0
0 < | x− x | < δ , ισχύουν οι σχέσεις | f( x) − a|
< ε ′ και | gx ( ) − b|
< ε ′ .
Εποµένως, | f( x) | − | a| ≤|| f( x) | −| a|| ≤| f( x) − a|
< ε ′ και άρα, | f ( x)| < ε ′ + | a|
. Εποµένως,
| f ( xgx ) ( ) −ab|
≤ | f ( x)|| g( x) − b| + | b|| f( x) − a|
< ( ε ′ + | a|) ε′ + | b|
ε′
= ( ε ′ + | a| + | b|)
ε ′.
ε
Αν λοιπόν ε ′ = min{1, } > 0 , τότε | f ( xgx ) ( ) − ab|
< ( ε ′ + | a| + | b|)
ε ′ ≤
1 + | a| + | b|
ε ′≤
ε
(1 + | a| + | b|) ε ′ ≤ (1 + | a| + | b|) = ε .
ε
1 + | a | + | b |
ε ′≤
1 + | a| + | b|
Για το (vii) παρατηρούµε ότι
x→x0
f ( x) a | bf( x) − ag( x)|
− = . Σύµφωνα µε τα (iv) και (v),
gx ( ) b | gx ( )|| b|
lim( bf ( x) − ag( x)) = 0. Έστω ε > 0. Τότε υπάρχει δ > 0 µε την ιδιότητα: Για κάθε x∈ A ,
1
µε 0 < | x− x0
| < δ , ισχύουν οι σχέσεις
− < και | gx ( ) − b| < | b|/2.
2
| bf ( x) ag( x)| ε | b | /2
(Σηµειώνουµε ότι ο αριθµός | b |/2 είναι θετικός).
Άρα | b| −| g( x) | ≤|| b| −| g( x) || ≤| b− g( x) | = | g( x) − b| < | b| / 2 και εποµένως, | b | < | g( x)|
, ήτοι
2
2
1 2 f( x) a | bf( x) − ag( x)| 2 ε | b|
< . Άρα, − = < = ε .
2
| g( x)| | b|
gx ( ) b | gx ( )|| b| 2| b|
Για το (viii) αρχικά παρατηρούµε ότι, σύµφωνα µε το (i) της πρότασης 5.1.5, θα έχουµε
a ≥ 0 και εποµένως ορίζεται η ρίζα k a . Έστω ε > 0 .
k
k
Αν a = 0, τότε, για ε′ = ε > 0, υπάρχει δ > 0 µε την ιδιότητα: 0 ≤ f( x)
< ε ′ = ε για κάθε
x∈ A , µε 0 < | x− x0
| < δ . Εποµένως
k
f( x)
< ε .

7
a
Υποθέτουµε ότι a > 0. Όπως στην απόδειξη του (vii) για την g, υπάρχει δ > 0 µε < f ( x)
2
για κάθε x∈ A , µε 0 < | x− x0
| < δ .
Εποµένως,
k−1 k−1
k
s k−− 1 s k −s k−1
∑ ( f( x)) a ∑ 2 a
s= 0 s=
0
> >
k −1
k −k k−1
∑
s=
0
2
a
k k k 1
= a − . Εφόσον
2
k
ε k a
2
k −1
> 0 ,
µπορούµε να υποθέσουµε ότι το δ είναι τέτοιο ώστε να ισχύει η επιπλέον σχέση
k k −1
ε k a
| f ( x) − a|
< , για κάθε x∈ A , µε 0 < | x− x0
| < δ .
2
k k −1
k
Εποµένως | k f ( x ) − a | f( x) − a|
ε k a 1
| = <
= ε ]. ■
k −1
1
k
s k−−
1 s 2
k k −
( f( x))
a
k a /2
∑
s=
0
Ας δούµε κάποιες εφαρµογές του παραπάνω θεωρήµατος:
5.1.7 Παραδείγµατα
1. Να υπολογιστούν τα όρια:
3
(i) lim( x 2x
1)
− + , (ii) lim( x− x )
2 − 2x+
4
x→−1
x→2
3 2
x − + x + x+
(iii) lim ( | x )
2 + 2x−2 | − x
2 + 8 , (iv) lim
| 1| 1
x→−1
x→0
2x
− 2
3 3 3
Λύση: (i) lim( x − 2x+ 1) = lim x − 2 lim x+ 1 = ( −1) −2( − 1) + 1= 2 .
x→−1 x→−1 x→−1
lim x− x − 2x+ 4 = lim x− lim( x − 2x+ 4) = 2 − 2 −2 ⋅ 2 + 4 = 0 .
(ii) ( )
(iii) ( )
2 2 2
x→2 x→2 x→2
lim | x + 2x−2| − x + 8 = lim | x + 2x−2| − lim x + 8 =
2 2 2 2
x→−1 x→−1 x→−1
2 2 2 2
x x x
x→−1 x→−1
= | lim( + 2 −2)| − lim( + 8) = |( − 1) + 2( −1) −2)| − ( − 1) + 8 = 3− 3=
0.
3 2
x x x
lim ( | x − 1| + x + x+
1)
x→0
(iv)
|
3
− 1| +
2
+ + 1
3
|0 − 1| +
2
0 + 0+
1
x→0
2x−2 lim(2x−2) 2⋅0−2
x→0
lim = = =−1
.
Στο προηγούµενο παράδειγµα ο υπολογισµός των ορίων έγινε ουσιαστικά µε απλή
αντικατάσταση στη θέση του x της οριακής του τιµής x
0
. Αυτό δεν είναι πάντοτε εφικτό,
όπως στην περίπτωση κατά την οποία έχουµε ένα κλάσµα του οποίου ο παρονοµαστής
µηδενίζεται απ’ αυτή την οριακή τιµή. Εφαρµόζουµε τότε άλλες τεχνικές:
2. Να υπολογιστούν τα όρια:
2
x + x−2
(i) lim , (ii)
x→−2
3
x + 8
(iv)
lim
x→−3
x
2
+ x+ 10 −4
, (v)
x + 3
lim
x→1
lim
x→2
2
3x
− 4x
+ 1
x
2
, (iii)
− 3x+
2
2
2x−1− x − 3x+
11
x
2
+ 5−3
.
lim
x→1
n+
1
x − ( n+ 1) x+
n
x −1
,

8
Λύση: (i)
2
x x x x x
lim lim lim
x →−2 3 x →−2 2 x →−2
2
−2−1 3
=− .
2
( −2) −2( − 2) + 4 4
+ − 2 ( + 2)( −1) −1
= = =
x + 8 ( x+ 2)( x − 2x+ 4) x − 2x+
4
2 2
3x − 4x+ 1 3x −3x− x+ 1 3 x( x−1) −( x−1)
( x−1)(3x−
1)
(ii) lim = lim = lim
= lim =
x →1 2
x − 3x+ 2 x →1 ( x−1)( x−2) x →1
( x−1)( x−2)
x→1
( x−
1)( x−
2)
3x
−1 3−1
lim = =−2
.
x→1
x −2 1−2
n+ 1 n+
1
n
x − ( n+ 1) x+ n x −x− nx+ n x( x −1) −n( x−1)
(iii) lim = lim = lim
=
x→1 x−1 x→1 x−1 x→1
x−1
n n−1 n−2
xx ( −1) xx ( − 1)( x + x + + x+
1)
lim − n= lim
− n=
x→1 x−1 x→1
x−1
n−1 n−2
lim( xx ( + x + + x+ 1)) − n= 1 ⋅ (1 + 1+ + 1) − n= n− n=
0.
x→1
n φορές
2
2 2
2
x x 10 4 ( x + x+ 10 ) −4
2
+ + − x + x+ 10 −16
(iv) lim
= lim
= lim
x→−3 x + 3 x→−3 2
x→−3 2
( x+ 3) ( x + x+ 10 + 4)
( x+ 3) ( x + x+ 10 + 4)
2
x + x− 6 ( x+ 3)( x−2) x−2
= lim = lim = lim
=
x→−3 x→−3 x→−3
2
( x+ 3) x + x+ 10 + 4 ( x+ 3) x + x+ 10 + 4 x + x+ 10 + 4
2
( −3) − 3+ 10 + 4
2 2
( ) ( )
−3−2 −5 5
= = =− .
4+
4 8
2
2 ⎛
2 2
( x + 5+ 3 ) ⎜(2x−1) −( x − 3x+
11)
2
⎛ 2 ⎞
2
⎜( ) ⎟( )
⎞
2
2x−1− x − 3x+ 11
⎟
(v) lim
= lim
⎝ ⎠
=
x→2 2
x→2
x + 5− 3 x + 5 −9 2x− 1+ x − 3x+
11
⎝
⎠
2 2 2 2 2
( x + 5+ 3)( 4x − 4x+ 1− x + 3x− 11)
( x + 5+ 3)( 3x −x−10)
lim
= lim
=
x→2 2 2 x→2
2 2
x + 5−9 2x− 1+ x − 3x+ 11 x −4 2x− 1+ x − 3x+
11
( )( )
( )
( )
2
( 2 + 5+ 3 )(3⋅ 2+
5)
11 .
2
4
( )
( )( )
( )
( )
2 2
x + 5+ 3 (3x+ 5)( x− 2) x + 5+ 3 (3x+
5)
= lim
= lim
=
x→2 2 x→2
2
( x− 2)( x+ 2) 2x− 1+ x − 3x+ 11 ( x+ 2) 2x− 1+ x − 3x+
11
= =
(2 + 2) 2⋅2 − 1+ 2 −3⋅ 2 + 11
2
x − ax+ 1 −bx
3. Να υπολογιστούν τα ab∈R , ώστε lim = 3 .
x→−1
x + 1
2
x − ax+ 1 −bx
Λύση: Εφόσον lim = 3 , τότε lim ( x )
2 − ax + 1 − bx =
x→−1
x + 1
x→−1
2
x − ax+ 1 −bx
2
lim lim( x + 1) = 3⋅ 0 = 0 . Άρα ( − 1) + a+ 1+ b= 0, δηλαδή b=− a+ 2 .
x→−1 x + 1 x→−1
2 2
x − ax+ 1−bx x − ax+ 1+ x a+
2
Εποµένως, lim
= lim
=
x→−1 x+ 1 x→−1
x+
1
=

9
2 2
x − ax+ 1 − x ( a+
2)
= lim
= lim
x→−1 2
( x 1) x ax 1 x a 2
− ax( x + 1) −( x − 1)( x + 1)
x→−1 2
+ ( − + − + ) ( x+ 1) ( x − ax+ 1− x a+
2)
(( a+ 1) x− 1)( x+ 1) ( a+ 1) x−1
=− lim
=− lim
=
x→−1 1
( x+ 1) x − ax+ 1− x a+
2 x − ax+ 1− x a+
2
2
x→−
2
( )
−a−1− 1 a+ 2 a+
2
=− = = .
1+ a+ 1+ a+ 2 2 a+
2 2
Θα πρέπει λοιπόν να έχουµε
b =− 34 + 2 =− 6 .
a + 2 = 3 . Από τη σχέση αυτή προκύπτει a = 34 και εποµένως,
2
=
⎛1
⎞
4. ∆είξτε ότι δεν υπάρχει το limsin ⎜ ⎟
x→0
⎝ x ⎠ .
⎛1
⎞
*Απόδειξη: Αν υπήρχε το limsin ⎜ ⎟, έστω αυτό a, τότε για ε = 1, θα υπήρχε δ > 0 µε την
x→0
⎝ x ⎠
1
ιδιότητα: sin ⎛ ⎜
⎞ ⎟ − a < 1, για κάθε x∈R µε 0 < | x | < δ .
⎝ x ⎠
2
Θεωρούµε τις ακολουθίες an
= , n=
1,2, … και
(4n
−1)
π
b n
2
= ,
(4n
+ 1) π
n = 1, 2, … Έχουµε,
⎛ 1 ⎞ ⎛ π ⎞
⎛ 1 ⎞ ⎛ π ⎞
sin ⎜ ⎟= sin⎜2nπ
− ⎟=−1
και sin ⎜ ⎟= sin⎜2nπ
+ ⎟=
1.
⎝an
⎠ ⎝ 2 ⎠
⎝bn
⎠ ⎝ 2 ⎠
Προφανώς lim a = limb
= 0 . Εποµένως υπάρχει n
0
µε | a | < δ και | b | < δ , για κάθε
n≥ n 0
.
n
n
y
1
n
y = sin(1/x)
n
-2/π
Ο
2/π
x
-1
Τότε θα είχαµε:
2 | 1 1| 1 a
=− − =− − −( )
⎛ 1 ⎞
−1− a = sin⎜
⎟− a < 1 και 1− a =
⎝an
⎠
άπειρη
ταλάν τωση
1
sin ⎛ ⎜
⎞ ⎟ − a < 1, για κάθε n≥
n0
. Άρα
⎝bn
⎠
1−a ≤ −1− a + 1− a < 1+ 1= 2, δηλαδή 2< 2, άτοπο.
Άλυτες ασκήσεις
1. Να υπολογιστούν τα όρια: (i)
x − a
(iv) lim
x → a x − a
3 3
4 4
, a > 0 .
x
lim
x→3
2
− 5x+
6
, (ii)
2
x − 9
lim
x→1
3 2
x x x
− 4 + 5 −2
, (iii)
4
x − 4x+
3
lim
x →0
3
( x 2) 8
+ − ,
x

10
2
2
x + 1−
2 x − x
2. Να υπολογιστούν τα όρια: (i) lim , (ii) lim
x→3
2
x→1
x + 7 − 4
x − 1
, (iii) x− 3− x − 4x+
3
lim
.
x→3
2
x − 9
f( x)
− x
3. Αν lim 3
x 2
2 = , να βρεθεί το lim f( x)
.
→ x − 4
x→2
2
bx − 1+ ax −x
− 1
4. Να υπολογιστούν τα ab∈ , R ώστε lim = 0 .
x→−1
x + 1
Στη συνέχεια ασχολούµαστε µε τα λεγόµενα πλευρικά όρια. Ας θεωρήσουµε τη συνάρτηση
| x |
f : R {0} → R µε f( x)
= . Η συνάρτηση αυτή δεν έχει όριο στο 0. Πράγµατι, αν
x
| x |
lim = a ∈R , τότε για ε = 1> 0, θα υπήρχε δ > 0 µε την ιδιότητα | x | a 1
x →0
x
x − < , για κάθε
x∈R µε 0 < | x | < δ .
1
−x
Προφανώς − δ ∈( − δ,0)
και 1 δ ∈ (0, δ ) . Αλλά, αν x∈( − δ ,0) τότε f( x) = =− 1 ενώ, αν
2 2
x
x
x∈ (0, δ ) , τότε f( x) = = 1.
x
y
1
x > 0
-δ
Ο
δ
x
x < 0
-1
1 1 1 1 1
Εποµένως, 2 =− | 1− 1| = | f ( − δ) − f( δ)| = |( f( − δ) − a) + ( f( δ) −a)| ≤| f( − δ) − a|
+
1
|( f ( δ ) − f ( δ )| < 1+ 1= 2, δηλαδή 2

11
i) Υποθέτουµε ότι το x
0
είναι σηµείο συσσωρεύσεως του συνόλου ( −∞, x0
) ∩ A. Θα λέµε ότι η f
συγκλίνει σ’ έναν αριθµό a∈R για x → x −
0
(ή µε τιµές µικρότερες του x
0
) αν lim f1( x)
= a,
όπου f ο περιορισµός της f στο σύνολο 1
( −∞, x0
) ∩ A. Ισοδύναµα, για κάθε ε > 0 υπάρχει
δ > 0 µε την ιδιότητα: x∈A∩( x0 −δ
, x0) ⇒| f( x) − a|
< ε .
x→x0
Συµβολίζουµε µε
lim f ( x)
x→x
−
0
τον αριθµό a.
y
lim x→x0 +
f(x)
x>x 0
lim x→x0 f(x)
x 0 υπάρχει δ > 0 µε την ιδιότητα: x∈ A∩( x0 −δ
, x0) ⇒| f( x) − a|
< ε .
Συµβολίζουµε µε
lim f ( x)
x→x
+
0
τον αριθµό a.
5.1.9 Πρόταση
Έστω f : A→ R µια συνάρτηση και x0
∈R σηµείο συσσωρεύσεως του Α. Υποθέτουµε ότι τα
πλευρικά όρια lim f ( x)
και lim f ( x)
υπάρχουν στο R .
Τότε το
x→x0
x→x
−
0
lim f ( x)
x→x
+
0
υπάρχει αν και µόνον αν
κοινή τιµή των πλευρικών ορίων ισούται µε το
x→x0
lim f ( x) = lim f( x)
. Στην περίπτωση αυτή, η
x→x −
0 x→x
+
0
lim f ( x)
.
x→x0
Απόδειξη: Προφανώς, αν το a= lim f( x)
υπάρχει, τότε lim f ( x) = lim f( x)
= a.
Υποθέτουµε ότι
ορίων.
Έστω ε > 0. Εφόσον
0 0
x→x −
0 x→x
+
0
x→x −
0 x→x
+
0
lim f ( x) = lim f( x)
και συµβολίζουµε µε a την κοινή τιµή των πλευρικών
lim f ( x)
= a, υπάρχει δ
1
> 0 µε την ιδιότητα: | f( x) − a|
< ε , για κάθε
−
x→x0
x∈A∩( x − δ , x ). Οµοίως, υπάρχει δ
2
> 0 µε την ιδιότητα: | f( x) − a|
< ε , για κάθε
x A x x δ
∈ ∩ (
0, 0
+ ). Θέτουµε δ δ1 δ2
έχουµε | f( x) − a|
< ε . ■
= min{ , } > 0 . Τότε, για κάθε x∈ A µε 0 < | x− x0
| < δ θα

12
5.1.10 Παραδείγµατα
1. Να βρεθούν (αν υπάρχουν) τα όρια: i)
f( x)
=
x
2
| x −x−2|
2
− 3x+ 2
.
Λύση: Παρατηρούµε ότι
lim f ( x)
x→−1
και ii)
lim f ( x)
, όπου
x→0
|( x+ 1)( x−
2)|
f( x)
=
. Το πεδίο ορισµού της f είναι το σύνολο
( x−1)( x−2)
R {1, 2} . Επίσης, ( x+ 1)( x−2) ≥ 0 αν και µόνον αν x ≤ − 1 ή x ≥ 2 και ( x+ 1)( x− 2) < 0 αν
και µόνον αν − 1< x < 2.
⎧ x + 1 , αν x≤− 1 ή x>
2
|( x+ 1)( x−2)| ⎪ x −1
Συνεπώς, f( x)
= =⎨
( x−1)( x−2)
⎪ x + 1 − , αν − 1 < x < 1 ή 1 < x < 2
⎪⎩
x −1
x + 1
⎛ x + 1⎞
Εποµένως, lim f ( x)
= lim = 0 και lim f ( x)
= lim 0
x→−1
−
x→−1
x −1
x→−1
+
⎜− ⎟=
. Άρα υπάρχει το
x→−1⎝
x −1⎠
lim f ( x)
και ισούται µε µηδέν.
x→−1
⎛ x + 1⎞
Ακόµη, lim f ( x)
= lim 3
x→2
−
⎜− ⎟=−
και
x→2
⎝ x −1⎠
lim f ( x)
.
x→2
x + 1
lim f ( x)
= lim = 3. Συνεπώς, δεν υπάρχει το
x→2
x −1
x→2
+
2. Να βρεθεί (αν υπάρχει) το lim
x→1
2
x x x
2
2x
−x−1
− 2 + 1− + 1
.
2 2
Λύση: Παρατηρούµε ότι x − 2x+ 1 = ( x− 1) και εποµένως
παράσταση λοιπόν
2
x x x
2
2x
−x−1
2
x x x
− 2 + 1− + 1
| x−1| − x+ 1 | x−1| − x+
1
ισούται µε =
.
2
2x − x−1 ( x− 1)(2x+
1)
Τώρα, αν x < 1 τότε | x− 1| − x+ 1 − x+ 1 − x+
1 2
= = − ενώ, αν
( x− 1)(2x+ 1) ( x− 1)(2x+
1) 2x
+ 1
x > 1 τότε | x− 1| − x+ 1 x− 1 − x+
= 1 = 0 .
( x− 1)(2x+ 1) ( x− 1)(2x+
1)
Συνεπώς,
lim
x→1
−
2
x x x
2
2 1
Άρα δεν υπάρχει το lim
− 2 + 1− + 1 ⎛ 2 ⎞ 2
= lim⎜− ⎟=−
και
x −x− x→1
⎝ 2 x + 1 ⎠ 3
x→1
2
x x x
2
2 1
− 2 + 1− + 1
.
x −x−
x→1
+
− 2 + 1 = | − 1| . Η
2
x − 2x+ 1− x+ 1
lim 0
2 = .
2x
−x−1
3. Να προσδιοριστεί το a ∈R ώστε να υπάρχει το όριο lim f ( x)
, όπου
x→1
⎧ 2
2x− x + 3 +
2 − <
⎪ ax
f( x)
= x −1
⎨
⎪ 2 a
2 x − , αν x≥1
⎪⎩ 2
1, αν x 1

13
Λύση: Παρατηρούµε ότι
⎛
2 2
2x− x + 3 ⎞
2 2x− x + 3
lim f ( x)
= lim + ax− 1 = lim
+
x→1 −⎜
x 1 ⎟ x→1
−
⎝
−
⎠
x−1
x→1
−
2
+ a −
Αλλά,
1.
2 2 2
2x− x + 3 4x −x −3 3( x− 1)( x+
1)
lim = lim = lim
=
x −1 ( x− 1) 2x+ x + 3 ( x− 1) 2x+ x + 3
2 2
( ) ( )
x→1 −
x→1 −
x→1
−
3( x + 1) 6 3
= lim = = . Εποµένως lim f ( x)
−
2+
4 2
x→1
x→1
−
2
2x+ x + 3
Ακόµη,
x→1 −
x→1
+
2
lim f( x) lim 2x
2
x→1 +
x→1
+
⎜ ⎟
lim f ( x) = lim f( x)
, δηλαδή,
3
− ή 1 . Εποµένως
2
1
= a 2 + .
2
⎛ a⎞
a
= − = − . Για να υπάρχει το όριο
⎝ 2⎠
2
3
a =− ή a = 1.
2
2 2
a 2 2a a 3 0 a
lim f ( x)
x→1
θα πρέπει
1 a
− 1±
25 −
+ = − ⇔ + − = ⇔ = = 1 ± 5 =
2 2 4 4
Άλυτες ασκήσεις
1. Να βρεθούν (αν υπάρχουν) τα όρια: i) lim f( x)
και ii) lim f( x)
, όπου
2. Να υπολογιστούν τα όρια: (i)
lim
x→−2
+
x→−3
x→2
2
x + 4x+
4
και (ii) lim
2
x + x−2
2
⎧ x − 3
⎪ , αν x < 3
3. ∆ίνεται η συνάρτηση f( x) = ⎨ x − 5
.
⎪ 2
⎩ax + 5 x, αν x ≥3
Να βρεθεί η τιµή του a, ώστε να υπάρχει το lim f( x)
.
x→3
x→−2
−
f( x)
=
x
2
x + 4x+
4
.
2
x + x−2
2
| x + x−6|
2
− 4x+ 3
.
5.1.11 Πρόταση
x x0
Ισχύει ότι lim a = a , όπου a > 0 .
x→x 0
*Απόδειξη: Η περίπτωση a = 1 είναι τετριµένη.
a x 0
y
Υποθέτουµε a > 1. Θεωρούµε την ακολουθία
1
bn
= x0
− , n = 1, 2, … Από την πρόταση 2.12.6
n
ε
y = a x
προκύπτει ότι b n x0
a < a και από το λήµµα 2.12.9
0
ότι lim
bn
x
a = a .
O
0
Έστω ε > 0. Εφόσον lim
bn
x
a = a , υπάρχει
1
0 0
δείκτης n
0
µε a x − ε < a bn
< a
x , για κάθε n≥ n0
. Έστω δ = x0
− b n
= .
0
n
0
b n0
δ
x 0
x
n0 x x0
= − δ < < τότε από την πρόταση 2.12.6, προκύπτει ότι a < a < a και λόγω
Αν b0 x0 x x0
b
x0 n0
x0 x x0
της σχέσης a − ε < a , παίρνουµε a − ε < a < a .
b

14
x 0 0
∆ηλαδή, | x x x
a − a | = a − a < ε . Σύµφωνα µε τον ορισµό του πλευρικού ορίου,
lim a
x→x
−
0
x x0
= a .
y
Με παρόµοιο τρόπο (θεωρώντας την
1
ακολουθία cn
= x0
+ , n = 1, 2, … )
n
2ε
προκύπτει ότι υπάρχει δείκτης n
1
µε
cn 1 x 0
a < a + ε , για κάθε n≥
n1
. Έστω
1
δ ′ = x0
− c n
= . Αν x
1
0
< x< x0
+ δ ′
n1
x0
x c n 1
τότε, x0 < x< cn 1
⇒ a < a < a και
y = a x
a x 0
O
x 0
2δ΄
c n1
x
c
n1 x0
λόγω της σχέσης a < a + ε , παίρνουµε
x0 x x0
x x0
a < a < a + ε ⇒| a − a | < ε .
x x0
Εποµένως lim a = a . Εφόσον lim
x
x x0
0
a = lim a = a , έπεται ότι lim a x x
= a . Η
x→x
+
0
x→x
−
0 x→x
+
x→x 0
0
x 1 1 x0
περίπτωση 0< a < 1 ανάγεται στην προηγούµενη, αφού lim a = = = a . ■
x→x
−1 x −1
x0
0 lim( a ) ( a )
x→x0
Αρκετές φορές δεν είµαστε σε θέση να υπολογίσουµε άµεσα το όριο µιας συνάρτησης. Σε
τέτοιες περιπτώσεις «εγκλωβίζουµε» τη συνάρτησή µας ανάµεσα σε δύο ισοσυγκλίνουσες
συναρτήσεις.
5.1.12 Πρόταση (Κριτήριο παρεµβολής )
Έστω ότι f ( x) ≤h( x) ≤ g( x)
για κάθε x∈(( x0 −δ
, x0) ∪ ( x0, x0
+ δ )) ∩ A, όπου δ > 0 .
Υποθέτουµε επίσης ότι lim f ( x)
= lim gx ( ) = a.
x→
0
x→x0
x→x0
Τότε το lim hx ( ) υπάρχει και είναι ίσο µε a.
x
Απόδειξη:
y
y = g(x)
Έστω ε > 0.
Επειδή lim f ( x)
= lim gx ( ) = a,
x→x0
x→x0
υπάρχει δ ΄ > 0, τέτοιο ώστε δ΄
< δ και
lim x→x0 h(x)
y = h(x)
| f( x) − a|
< ε και | gx ( ) − a|
< ε , για
y = f(x)
κάθε x∈ A , µε 0 < | x− x0
| < δ΄
.
Από τη σχέση | f( x) − a|
< ε προκύπτει
O
x -d x 0 -δ
0
x 0
+d +δ
x
ότι − ε < f ( x)
− a και από τη σχέση

15
| gx ( ) − a|
< ε προκύπτει ότι gx ( ) − a< ε .Εφόσον f ( x) − a≤h( x) −a≤ g( x)
− a, οι δύο
αυτές σχέσεις µας δίνουν:
− ε < hx ( ) − a< ε ⇔| hx ( ) − a|
< ε , για κάθε x∈ A , µε 0 < | x− x0
| < δ΄
. ■
5.1.13 Παραδείγµατα
2
x sin ( 1/ x)
1. Να δειχθεί ότι lim = 0 .
x→0
x + 1
⎛ 1 1⎞
Απόδειξη: Εφόσον x → 0, µπορούµε να περιοριστούµε στο διάστηµα ⎜−
, ⎟
⎝ 2 2⎠ .
⎛ 1 1⎞
Αν x∈ ⎜ − , ⎟
⎝ 2 2⎠ τότε x + 1 > 0 και εποµένως | x + 1| = x + 1 .
2 2
2
2 2
x sin(1/ x)
x sin(1/ x)
x
x 0
Παρατηρούµε ότι 0 ≤ = ≤ και επιπλέον lim =
x + 1 x+ 1 x+
1
x→0
x + 1 0+
1 = 0 .
2
x sin(1/ x)
Από το κριτήριο της παρεµβολής προκύπτει ότι lim = 0 που είναι ισοδύναµο µε
x→0
x + 1
2
x sin(1/ x)
το ότι lim = 0 .
x→0
x + 1
2. Να δειχθεί ότι
x
e − 1
lim = 1 .
x→0
x
x
Απόδειξη: Γνωρίζουµε ότι e ≥ 1+ x, για κάθε x∈R (πόρισµα 2.12.11). Θέτοντας − x αντί
− x
x 1
x, παίρνουµε e ≥1− x. Αν x < 1, τότε η τελευταία σχέση συνεπάγεται ότι e ≤ 1 − x
.
x 1
Εποµένως, 1+ x≤e
≤ , για κάθε x < 1 .
1 − x
x
x
e −1 1
1
e − 1
Αν x∈ (0,1) , τότε 1≤ ≤ . Επειδή lim = 1 , έπεται ότι lim = 1 .
x 1 − x
x→0
1−
x
x→0
+
x
x
x
e −1 1
1
e − 1
Αν x < 0 , τότε 1≥ ≥ και επειδή lim = 1 , έπεται ότι lim = 1 .
x 1 − x
x→0
1−
x
x→0
−
x
x
e − 1
Εφόσον τα δύο πλευρικά όρια είναι ίσα, προκύπτει ότι lim = 1 .
x→0
x
Η επόµενη πρόταση µας επιτρέπει να αλλάζουµε τη µεταβλητή όταν υπολογίζουµε όρια.
5.1.14 Πρόταση
∆ίνονται οι συναρτήσεις g:
A→B⊆R και f : B→ R . Υποθέτουµε ότι:
(i)
lim gx ( ) = a και g( x)
≠ a για κάθε x που ανήκει σε µια περιοχή (( x0 −δ
, x0) ∪ ( x0,
x x
→ 0
x0 + δ )) ∩ A του x
0
(χωρίς το x
0
).
(ii) lim f ( u ) = b .
u→a

16
Τότε
lim f ( gx ( )) = b.
x→x0
*Απόδειξη: Έστω ε > 0 . Εφόσον lim f ( u ) = b , υπάρχει δ ΄ > 0 µε την ιδιότητα
u→a ( u∈ B και 0 < | u− a| < δ΄) ⇒| f( u) − b|
< ε . (1)
Εφόσον
lim gx ( ) = a , υπάρχει δ ΄΄ > 0 µε την ιδιότητα
x x
→ 0
( x∈ A και 0 < | x− x0
| < δ΄΄) ⇒| gx ( ) − a|
< δ΄
. (2)
Μπορούµε να υποθέσουµε ότι δ΄΄
< δ , οπότε ισχύουν ταυτόχρονα η (2) και η σχέση
g( x)
≠ a. Εποµένως 0 < | gx ( ) − a|
< δ΄
, για κάθε x∈(( x0 −δ ′′, x0) ∪( x0,
x0 + δ ′′))
∩ A .
g
f
x 0 -δ΄΄
x 0
x 0 +δ΄΄
b-ε
b
b+ε
a-δ΄ a a+δ΄
Συνδυάζοντας τις σχέσεις (1) και (2), παίρνουµε
( x∈ A και 0 < | x− x | < δ ′′)
⇒| f( g( x)) − b|
< ε . ■
0
5.1.15 Παράδειγµα
2
Να υπολογιστεί το όριο lime
x x
Λύση: Παρατηρούµε ότι
x→1
2 − + 1
.
2
lim(2x
x 1) 2
x→1
− + = . Ακόµη, η παράσταση
u x x
2
= 2 − + 1 είναι
διάφορη του 2, για κάθε x∈( −1/2,1) ∪ (1, +∞. ) (Μελέτη τριωνύµου).
Εδώ έχουµε τις συναρτήσεις f : R → (0, +∞)
µε f ( u)
2
g : R→
R µε g( x ) = 2x
− x + 1.
2
2 1 2
Ακόµη, lim gx ( ) = 2 . Άρα lim
x − x +
e = lime u = e .
x→1
x→1 u→2
u
= e και
Άλυτες ασκήσεις
[1/ x]
x( −1)
1. Να υπολογιστεί το όριο: lim , όπου [ x ] είναι το ακέραιο µέρος του x.
x→0
2
x + 1
x
x
2
−
e − e
2 x−
e 1
− e 2
2. Να υπολογιστoύν τα όρια: (i) lim και (ii) lim
x→1
2
x −1
x→3
x − 2x−
3
5.1.16 Πρόταση (Όρια τριγωνοµετρικών συναρτήσεων)
Ισχύουν τα εξής:
i) lim sin x = sin x , ii) lim cos x = cos x και
x→x0
0
x→x0
0
π
iii) lim tan x = tan x0
, όπου x0
≠ kπ
+ .
x→x0
2
Απόδειξη: Το (iii) προκύπτει από τα (i) και (ii) του θεωρήµατος 5.1.6. Θα αποδείξουµε
λοιπόν τα (i) και (ii).

17
Αρχικά δείχνουµε ότι
limsin x = 0 και
x→0
limcos x = 1.
x→0
Εφαρµόζουµε ένα γεωµετρικό επιχείρηµα. Θεωρούµε
τον τριγωνοµετρικό κύκλο.
Έχουµε
|sin x | =ΟΒ=ΑΜ0
M
x
A O΄
x

18
x>0
x 0
Στην περίπτωση αυτή έχουµε
sin x 1 sin x sin x
sin x< x< tan x⇔ < 1< ⇔ cos x< < 1.
x> 0 x cos x x cosx>
0 x
Περίπτωση 2: x < 0
Στην περίπτωση αυτή έχουµε
ΑΜ = sin x , µήκος τόξου Ο΄Μ = x και Ο΄Ν = tan x . Άρα
ΑΜ = − sin x , µήκος τόξου Ο΄Μ = − x και Ο΄Ν =− tan x .
sin x 1 sin x sin x
Άρα − sin x
0 x
sin x
Σε κάθε περίπτωση έχουµε cos x < < 1 . Αλλά limcos x = cos0 = 1. Από το κριτήριο
x
x→0
sin x
παρεµβολής παίρνουµε lim = 1.
x→0
x
sin x
Η γραφική παράσταση της συνάρτησης y = , x≠ 0 είναι η ακόλουθη:
x
y=
sinx
x
1
-2π -π
Ο
π
2π
Είναι µια συνεχής καµπύλη, χωρίς το σηµείο (0, 1).
cos x − 1
(ii) Για την απόδειξη του τύπου lim = 0 χρησιµοποιούµε την τριγωνοµετρική
x→0
x

19
2 x x
−2sin
sin
2 x
cos x − 1
ταυτότητα cos x = 1−
2sin . Έχουµε λοιπόν:
2 2 x
= =− sin . Θέτοντας
2 x x x 2
2
x
cos x − 1 ⎛sinu
⎞
u = → 0 , παίρνουµε (µε βάση την πρόταση 5.1.14) lim = − lim sin
2
x
⎜ u ⎟=
→0
x
u→0
⎝ u ⎠
sinu
=−lim
⋅limsin u =−1⋅ 0 = 0 . ■
u→0
u u→0
5.1.18 Παραδείγµατα
2
tan x sin ax
1. Να υπολογιστούν τα όρια: i) lim , ii) lim , όπου ab ≠ 0 ,
x →0
x
x→0
sin bx
cos 2x
− cos 4x
iii) lim
.
x→0
xsin
x
2
tan x ⎛ tan x sin x⎞
tan x sin x tan 0 0
Λύση: i) lim = lim⎜
⎟= lim ⋅ lim = ⋅ 1 = ⋅ 1 = 0 .
x→0 x x→0 cos x x x→0cos x x→0
⎝ ⎠
x cos0 1
sin ax a ⎛sin ax bx ⎞ a sin ax bx
sin ax
ii) lim = lim⎜
⎟=
lim lim . Για το lim , θέτουµε
x→0sinbx b x→0 ax sinbx b x→0 ax x→0
⎝
⎠
sinbx
x →0
ax
sin ax sin u
bx u
u = ax→ 0 . Εποµένως, lim = lim = 1 . Όµοια, lim = lim =
x→0 ax u→0
u
x→0
sin bx u→0
sin u
1
sin ax a
= = 1. Άρα lim = .
sinu
x→0
lim
sin bx b
u →0
u
iii) Εδώ χρησιµοποιούµε την τριγωνοµετρική ταυτότητα:
a+ b b−
a
cos a− cosb= 2sin sin .
2 2
2x + 4x 4x−
2x
2sin sin
cos 2x−
cos 4x
Έχουµε λοιπόν : lim
lim 2 2 sin3xsin
x
= = 2lim =
x→0 xsin
x x→0
xsin
x
x→0
xsin
x
sin 3x
= 6⋅ lim = 6⋅ 1= 6.
x→0
3x
2
( x + 1)sinx
3sin x
2. Να υπολογιστούν τα όρια: i) lim
, ii) lim
x →0
2
x − x
x → 0 1 − x + ,
1
sin x − 1 2cos2x
−1
cos x − 1
iii) lim , iv) lim και v) lim
x→ π
2 cos x
x→ π
6 4sin x − 2
x→0
2 .
x
2 2 2
( x + 1)sinx ⎛ x + 1sinx⎞
0 + 1
Λύση: i) lim = lim 1 1
x 0
2
⎜ ⎟= ⋅ =− ,
→ x −x x→0
⎝ x−1 x ⎠ 0−1
3sin x sin x x x x(1 + x+
1)
ii) lim = 3⋅ lim lim = 3⋅ lim = 3⋅ lim =
x→0 1 − x+ 1
x→0 x x→0 1 − x+ 1
x→0 1 − x+
1
x→0
1 −x−
1
−3lim(1 ⋅ + x + 1) =−32 ⋅ =− 6.
x→0
π
sin x − 1 cos( 2
−x)
−1
π
iii) lim lim
x π
= . Θέτουµε u = −x→ 0 . Εποµένως,
→ 2 cos x x→π
π
2 sin − x
2
( )
2
sin x−1 cosu−1 cosu−1
u
lim = lim = lim lim = 0 ⋅ 1 = 0 .
x→ π 0 0 0
2 cos x u→ sin u u→ u u→
sin u

20
π
iv) Θέτουµε u = x− → 0 . Εποµένως, x= u+ π .
6
6
⎛ π ⎞
π π π
Άρα, 2cos2x− 1 = 2cos⎜2( u+ ) ⎟− 1 = 2cos(2 u+ ) − 1 = 2cos 2ucos −2sin 2usin − 1=
⎝ 6 ⎠
3 3 3
2
= cos 2u− 3 sin 2u− 1 = 1−2sin u−2 3sin ucosu− 1 =− 2sin u(sin u+ 3 cos u)
.
π π π
Ακόµη, 4sin x− 2 = 4sin( u+ ) − 2 = 4sinucos + 4cosusin − 2 =
6 6 6
3 1
= 4sin u⋅ + 4cosu⋅ − 2 = 2( 3 sinu+ cosu− 1) .
2 2
2cos2 1 2sin (sin 3 cos ) sin
Εποµένως, x − − u u +
= u =− (sin u+
3 cos u)
u
4sin x − 2 2( 3sin u+ cosu−1)
u
1 sinu
1
=− (sin u+
3 cos u)
.
3sinu+ cosu− 1 u sinu
cosu−1
3 +
u
u u
2cos2x
−1
sin u
1
Έχουµε λοιπόν: lim =− (sin 0 + 3 cos0) ⋅lim
⋅
x→ π
6 4sin x − 2
u→0
u sin u cosu−1
3lim + lim
u→0 u u→0
u
1
=− 31 ⋅ ⋅
3+ 0
= − 1.
2 x
2 x
1−2sin −1 sin
cos x − 1 1 1 1
v) lim lim 2 lim 2 1
0
2 =
x x 0
2 =−
0
2 =− ⋅ =− .
→ x → x 2 x→
⎛ x ⎞ 2 2
⎜ ⎟
⎝2
⎠
Άλυτες ασκήσεις
sin 2x
sin x
1. Να υπολογιστoύν τα όρια: (i) lim
x → 0
2
x + x
, (ii) e − 1 1−
cos2x
x − tan x
lim , (iii) lim , (iv) lim ,
x→0
2
x
x →0
x
x →0
x
sin 5x
(v) lim
x→ 0 5 x + 4 − .
2
⎛2x
−π
⎞
tan
1 1
⎜ ⎟
⎛
⎞
2. Να υπολογιστoύν τα όρια: (i) lim⎜
− ⎟
x→0
⎝ sin x tan x ⎠ και (ii) 3
lim
⎝ ⎠
.
π
x→
π
2 x −
2
sin x − x
sin
3. Να υπολογιστεί το όριο: lim
x →0
2 . (Υπόδειξη: Χρησιµοποιείστε την ανισότητα cos x < x < 1
x
x
cos x−1 sin x−x
της απόδειξης της πρότασης 5.1.13 για να καταλήξετε στη σχέση < < 0 . Στη
2
x x
συνέχεια χρησιµοποιήστε το (ii) της πρότασης 5.1.3).
Στα προηγούµενα αναφερθήκαµε σε όρια συναρτήσεων που είναι πραγµατικοί αριθµοί και
όχι −∞ ή +∞ . Όπως καταλαβαίνει κανείς, αυτό δεν είναι ο κανόνας. Ας δούµε το ακόλουθο
παράδειγµα:

21
1
Θεωρούµε τη συνάρτηση f :( −∞,0) ∪ (0, + ∞)
→ R µε τύπο f( x)
= . Η γραφική της
2
x
παράσταση είναι η ακόλουθη:
y
Παρατηρούµε ότι συνάρτηση παίρνει ολοένα πιο
µεγάλες τιµές, καθώς το x πλησιάζει στο µηδέν.
Λέµε ότι η συνάρτηση τείνει στο +∞ για x → 0
1
και γράφουµε lim =+∞. Ας διατυπώσουµε
x →0
2
x
τώρα τον σχετικό ορισµό:
4
1
1/4
-2 -1 -1/2 O 1/2 1 2
x
5.1.19 Ορισµός
Έστω f : A→ R µια συνάρτηση και x0
∈R σηµείο συσσώρευσης του πεδίου ορισµού της Α.
i) Θα λέµε ότι η συνάρτηση f συγκλίνει για x → x0
στο +∞ αν, για κάθε ε > 0 (οσοδήποτε
µεγάλο) υπάρχει δ > 0 µε την ιδιότητα:
Γράφουµε
Αν x∈ A και 0 < | x− x0
| < δ , τότε f( x)
> ε .
lim f( x)
= +∞ .
x→x0
ii) Θα λέµε ότι η συνάρτηση f συγκλίνει για x → x0
στο −∞ αν, για κάθε ε > 0 (οσοδήποτε
µεγάλο) υπάρχει δ > 0 µε την ιδιότητα:
Γράφουµε
lim f( x)
= −∞ .
x→x0
Αν x∈ A και 0 < | x− x0
| < δ , τότε f( x)
< − ε .
Επίσης, αν f είναι ο περιορισµός της f στο σύνολο 1
A∩ ( x0, +∞ ) και f
2
ο περιορισµός της
στο A ∩( −∞ , x0
), τότε θέτουµε:
α) lim f( x)
=+∞ αν lim f ( x)
= +∞ ,
x→x
+
0
x→x
+
0
x→x0
β) lim f( x)
=−∞ αν lim f ( x)
= −∞ ,
x→x
−
0
x→x0
γ) lim f( x)
=+∞ αν lim f ( x)
= +∞ και
x→x
−
0
x→x0
δ) lim f( x)
=−∞ αν lim f ( x)
= −∞ .
x→x0
1
1
2
2
Για τον υπολογισµό απειριζόµενων ορίων είναι χρήσιµη η ακόλουθη πρόταση:

22
5.1.20 Πρόταση
Έστω f, g:
A→ R συναρτήσεις και x0
∈R σηµείο συσσώρευσης του κοινού πεδίου ορισµού
Α. Ισχύουν τα εξής:
i) Αν f ( x) ≤ g( x)
για κάθε x∈ A και lim f( x)
= +∞ , τότε lim ( ) = +∞ .
x→x0
x→x0
gx
x→x0
ii) Αν f ( x) ≤ g( x)
για κάθε x∈ A και lim gx ( ) = −∞ , τότε lim f( x)
= −∞ .
iii)
iv)
Αν lim f( x)
= a∈R ή lim f( x)
= +∞ και lim ( ) = +∞ ,
τότε
x→x0
x→x0
x→x0
lim[ f( x) + g( x)]
=+∞.
x→x0
x→x0
gx
x→x0
Αν lim f( x)
= a∈R ή lim f( x)
= −∞ και lim gx ( ) = −∞ ,
τότε
lim[ f( x) + g( x)]
=−∞.
x→x0
x→x0
gx
x→x0
x→x0
x→x0
v) Αν lim f( x)
= a∈R µε a > 0 και lim ( ) = +∞ , τότε lim[ f( x) g( x)]
=+∞.
vi)
vii)
x→x0
x→x0
x→x0
Αν lim f( x)
= a∈R µε a > 0 και lim gx ( ) = −∞ , τότε lim[ f( x) g( x)]
=−∞.
x→x0
gx
x→x0
gx
x→x0
x→x0
Αν lim f( x)
= a∈R µε a < 0 και lim ( ) = +∞ , τότε lim[ f( x) g( x)]
=−∞.
x→x0
x→x0
Αν lim f( x)
= a∈R µε a < 0 και lim ( ) = −∞ , τότε lim[ f( x) g( x)]
=+∞.
Αν lim f( x) = lim g( x)
=+∞ ή lim f( x) = lim g( x)
=−∞, τότε lim[ f( x) g( x)]
=+∞.
x→x0 x→x0
x→x0
x→x0
x→x0 x→x0
viii) Αν lim f( x)
=+∞ ή lim f( x)
= −∞ , τότε
ix)
1
lim = 0 .
( )
x→x0
f x
x→x0
1
Αν lim f( x) = 0 και f( x ) > 0 για κάθε x∈ A , τότε
x→x0
x x f x
Αν
lim f( x) = 0 και f( x ) < 0 για κάθε x∈ A , τότε
x→x0
lim
→ 0 ( )
1
lim
x→x0
f ( x )
x→x0
= +∞ .
= −∞ .
x) Αν f( x) ≥ 0 για κάθε x∈ A και
lim f( x)
= +∞ τότε
x→x0
lim
k
f( x)
= +∞ ,
x→x0
όπου k θετικός ακέραιος.
*Απόδειξη: Οι (i) και (ii) προκύπτουν άµεσα από τον ορισµό.
Για το (iii) θεωρούµε ένα ε > 0 . Αν lim f ( x)
= a τότε υπάρχει δ
1
> 0 µε την ιδιότητα:
( x A και 0 | x x | δ )
0 1
x→x0
∈ < − < ⇒ | f( x) − a| < | a| + 1.
Η σχέση | f( x) − a| < | a| + 1 συνεπάγεται τη σχέση f( x) > a−| a| − 1. Παρατηρούµε ότι
a≤ | a| < | a| + 1 και συνεπώς a− | a| − 1< 0 (άρα − a+ | a| + 1> 0). Ακόµη, επειδή
lim gx ( ) =+∞, υπάρχει
2
0
x→x0
δ > µε την ιδιότητα: ( x A και 0 | x x | δ )
∈ < − < ⇒
0 2
gx ( ) > ε − a+ | a| + 1> 0. Αν δ = min{ δ1, δ2}
, τότε για κάθε x∈ A µε 0 < | x− x0
| < δ , θα
συναληθεύουν οι σχέσεις f( x) > a−| a| − 1 και gx ( ) > ε − a+ | a| + 1> 0. Με πρόσθεση κατά
µέλη προκύπτει η επιθυµητή ανισότητα. Αν lim f( x) = lim g( x)
=+∞, τότε επιλέγουµε τα
x→x0 x→x0
δ1, δ
2
> 0 ώστε να ισχύουν οι ανισότητες f( x) > ε /2 και gx ( ) > ε /2.
Η (iv) προκύπτει µε ανάλογο τρόπο.

23
Για την (v) υποθέτουµε αρχικά ότι
Εφόσον
x→x0
lim ( ) = +∞ . Θεωρούµε ένα ε > 0 . Τότε και 2 ε / a > 0.
gx
x→x0
lim f ( x)
= a, υπάρχει δ
1
> 0 µε την ιδιότητα: ( x A και
0 < | x− x | < δ ) ⇒
∈
0 1
| f ( x) − a| < a/2. Η σχέση | f ( x) − a| < a/2
συνεπάγεται τη σχέση f ( x) > a/2. Ακόµη,
επειδή lim gx ( ) =+∞, υπάρχει
2
0
x∈ A και 0 < | x− x | < δ ⇒
x→x0
δ > µε την ιδιότητα: ( )
0 2
g( x) > 2 ε / a. Αν δ = min{ δ1, δ2}
, τότε για κάθε x∈ A µε 0 < | x− x0
| < δ , θα συναληθεύουν
a 2ε
οι σχέσεις f ( x) > a/2
και g( x) > 2 ε / a. Εποµένως και η σχέση f( x) g( x)
> ⋅ = ε . Αν
2 a
lim ( ) =−∞, το δ
2
> 0 επιλέγεται έτσι ώστε g( x) < − 2 ε / a, για κάθε x∈ A µε
gx
x→x0
0 < | x− x | < δ .
0 2
Η απόδειξη της (vi) είναι παρόµοια.
Για την (vii) αρκεί να βρούµε δ > 0 µε f( x ) > 1 και gx ( )
lim f( x) = lim g( x)
=+∞ και f( x ) < − 1 και gx ( ) < − ε , στην περίπτωση
x→x0 x→x0
lim gx ( ) =−∞, για κάθε x∈ A µε 0 < | x− x0
| < δ .
x→x0
Για την (viii) υποθέτουµε αρχικά ότι
την ιδιότητα
lim f( x)
x→x0
lim f( x)
x→x0
> ε , στην περίπτωση
lim f ( x)
=
x→x0
= +∞ . Έστω ε > 0. Τότε υπάρχει δ > 0 µε
1
f( x) > 1/ ε ⇔ 0< < ε , για κάθε x∈ A µε 0 < | x− x0
| < δ . Αν
f( x)
=−∞, τότε υπάρχει δ > 0 µε την ιδιότητα
x∈ A µε 0 < | x− x0
| < δ .
1
f( x) < −1/ ε ⇔− ε < < 0, για κάθε
f( x)
Για την (ix) θεωρούµε δ > 0 µε την ιδιότητα 0 < f( x) < 1/ ε (στην περίπτωση που
f( x ) > 0), για κάθε x∈ A µε 0 < | x− x0
| < δ . Τότε f( x)
εξετάζεται παρόµοια.
k
Για το (x) θεωρούµε ε > 0. Τότε και ε > 0. Εφόσον
ιδιότητα: ( x A και 0 | x x | δ )
0
lim f( x)
x→x0
> ε . Η δεύτερη περίπτωση
= +∞ , υπάρχει δ > 0 µε την
k
∈ < − < ⇒ f( x)
> ε ⇒
k
f( x)
> ε και τελειώσαµε. ■
5.1.21 Παραδείγµατα
k
1. Έστω k θετικός ακέραιος. Παρατηρούµε ότι αν ο k είναι άρτιος τότε x > 0, για κάθε
k
1
x ≠ 0 . Εφόσον lim x = 0 , από (ix) της προηγούµενης πρότασης προκύπτει ότι lim
x→0
x→0
x k
=+∞.
k
k
1
Αν ο k είναι περιττός τότε x > 0, για x > 0 ενώ, x < 0 , για x < 0. Άρα lim k
=+∞ και
x→0
+
x
1
lim k
=−∞.
x→0
−
x
1
Στο επόµενο σχήµα δίνεται η γραφική παράσταση της συνάρτησης f( x) = , για k = 1.
k
x

24
y
+∞
O
x
-∞
2
2
2
+ 3 x − x−
6 | x −x−2|
2. Να υπολογιστούν τα όρια: i) lim , ii) lim , iii) lim
x →0
−
xx | |
2
x x→2
| x − 4|
+ 3
x→−1
− x + 3x+ 2
.
2
Λύση: i) Παρατηρούµε ότι lim ( x + 3) = 3 > 0 , lim (| x| x) = 0 και για κάθε x < 0 έχουµε
x→0
−
| x| x< 0. Συνδυάζοντας το (v) και το (ix) της προηγούµενης πρότασης, συµπεραίνουµε ότι
2
+ 3 =−∞.
x
xx x
lim
→0
− | |
ii) Παρατηρούµε ότι
− − =− < ,
2
lim( x x 6) 4 0
x→2
x→0
−
2
lim | x 4 | 0
x→2
−
2
| x − 4| > 0. (Μπορούµε να υποθέσουµε ότι x ≠ − 2 , γιατί x → 2 ).
2
x −x−6
Εποµένως, lim =−∞.
x→2
|
2
x − 4|
− = και για κάθε x ≠± 2 έχουµε
2
3 2
iii) Παρατηρούµε ότι x −x− 2 = ( x+ 1)( x− 2) και − x + 3x+ 2 =− ( x+ 1) ( x− 2) .
2
| x −x− 2| | x+ 1|| x−2| | x−2|
Εποµένως,
=− =−
. Εφόσον x →− 1< 2, x − 2<
0
3 2
− x + 3x+ 2 ( x+ 1) ( x− 2) | x+ 1|( x−2)
και άρα | x− 2| =−( x− 2) .
2
| x −x−2| 1
Συνεπώς,
=
3
x −3x− 2 | x+ 1|
για κάθε x ≠− 1. Εποµένως,
, για κάθε 1 x 2
− < < . Ακόµη, lim | x + 1| = 0 και | x + 1| > 0
x 1
+
2
| x x 2| 1
lim
lim
3
x→−1 + x→−1
+
→−
− −
= =+∞.
− x + 3x+ 2 | x+
1|
2. Να δειχθεί ότι lim
και lim
π
+
⎛ ⎞
x→ ⎜kπ
+ ⎟
⎝ 2 ⎠
x→( π /2)
−
tan x =−∞.
tan x =+∞ και
lim
x→−
( π /2)
+
tan x = −∞ . Γενικότερα,
lim
π
−
⎛ ⎞
x→ ⎜kπ
+ ⎟
⎝ 2 ⎠
tan x =+∞

25
π
π
Απόδειξη: Παρατηρούµε ότι lim sin x = sin = 1 > 0 , lim cos x = cos = 0 και
x→( π /2)
−
2
x→( π /2)
−
2
⎛ π ⎞
cos x > 0 για κάθε x∈ ⎜ 0, ⎟
⎝ 2 ⎠ . Σύµφωνα µε την προηγούµενη πρόταση, lim tan x =
x→( π /2)
−
= sin x
lim
x →( π /2)
− cos x
=+∞. Η απόδειξη της ισότητας lim tan x = −∞ είναι παρόµοια.
x→−
( π /2)
+
-3π -2π -π π
2π
3π
5π
2
3π
2
π
2
O
π
2
3π
2
5π
2
Για τη γενική περίπτωση, αρκεί να θυµηθούµε ότι η συνάρτηση
π
π
περίοδο π. (Επιπροσθέτως, kπ
+ = ( k + 1) π − ). ■
2 2
y = tan x είναι περιοδική µε
Άλυτες ασκήσεις
2
3x
+ 4
1. Να υπολογιστoύν τα όρια: (i) lim
x→1
3 2
x − 2x + x
, (ii) x + 7
lim
2
x→−2
−
x − 4
, (iii) x − 2x+
2
lim ,
x →−1
+ | x | − 1
(iv)
lim
x→1
−
3 2
x x x
+ + + 1
, (v)
2
x − 3x+
2
2. Να υπολογιστoύν τα όρια: (i) lim
⎛
π ⎞
⎜x + ⎟tan
x
⎝ 2 ⎠
x →− ( π /2)
+
lim sin(2 x + π )
x→( π /2)
−
f( x)
3. Να βρείτε το lim f( x)
, όταν: (i) lim = −∞
x→1
x→1
x − 2
.
2
2
x + x + 1 x − 4x−
5
, (ii) lim
, (iii) lim
tan x
x→4
+ 2
x + 9−
5
και (ii) lim ( f( x)(3x
2 − 2) )
x→1
x→5
−
=+∞.
2
x + 9−5
2
x −4x− 5
.

26
5.2 Όριο συνάρτησης για x→ + ∞ ή x→ −∞
Θεωρούµε τη συνάρτηση µε τύπο
ακόλουθη:
f( x)
=
x
2
2x
x 1
y
2
− −
. Η γραφική της παράσταση είναι η
+ x+ 1
2
-∞ 1 O
x
+∞
Παρατηρούµε ότι καθώς το x αυξάνει και τείνει στο +∞ η τιµή της συνάρτησης τείνει προς
τον αριθµό 2. Αντίστοιχη εικόνα παρουσιάζει η συνάρτηση καθώς το x τείνει στο −∞ .
Ο ακριβής εψιλον-τικός ορισµός αυτής της ιδιότητας είναι ο εξής:
5.2.1 Ορισµός
Θεωρούµε µια συνάρτηση f : A→ R .
i) Υποθέτουµε ότι, για κάθε δ > 0 , το Α περιέχει ένα τουλάχιστον στοιχείο του διαστήµατος
( δ , +∞ ). Θα λέµε ότι η συνάρτηση συγκλίνει στο a∈R για x →+∞, αν για κάθε ε > 0
υπάρχει δ > 0 , τέτοιο ώστε: | f( x) − a|
< ε , για κάθε x∈ A∩ ( δ , +∞ ).
ii) Υποθέτουµε ότι, για κάθε δ > 0 , το Α περιέχει ένα τουλάχιστον στοιχείο του διαστήµατος
( −∞, − δ ). Θα λέµε ότι η συνάρτηση συγκλίνει στο a∈R για x →−∞, αν για κάθε ε > 0
υπάρχει δ > 0 , τέτοιο ώστε: | f( x) − a|
< ε , για κάθε x∈ A∩( −∞, − δ ).
5.2.2 Παρατήρηση
Γνωρίζουµε ότι οι ακολουθίες πραγµατικών αριθµών είναι συναρτήσεις µε πεδίο ορισµού το
σύνολο N = {0,1, 2, …}
ή το σύνολο N {0} = {1, 2,3, …}
. Επίσης, για κάθε δ > 0 , το σύνολο
N ∩ ( δ , +∞)
είναι µη κενό. Κατά συνέπεια, οι συγκλίνουσες ακολουθίες αποτελούν ειδική
περίπτωση των συγκλινουσών (για x →+∞) συναρτήσεων. Ορθότερο λοιπόν θα ήταν να
γράφουµε lim a
n→+∞
n
για το όριο µιας ακολουθίας ( a
n ) , αντί του lim a n
.
Είναι θέµα ρουτίνας για τον εξοικειωµένο µε την εψιλοντική διαδικασία αναγνώστη να
αποδείξει ότι ισχύουν και εδώ αντίστοιχα αποτελέσµατα µε αυτά των 5.1.4 και 5.1.6. Η µόνη

27
διαφορά είναι ότι, αντί να παίρνουµε το ελάχιστο από τα εµπλεκόµενα δ, παίρνουµε το
µέγιστο από αυτά.
5.2.3 Πρόταση (µοναδικότητα του ορίου)
Υποθέτουµε ότι η συνάρτηση f τείνει, για x →+∞ (ή για x →−∞), προς τους αριθµούς a
1
και
a
2
. Τότε a1 a2
= . ■
Η παραπάνω πρόταση µας επιτρέπει να συµβολίζουµε το µοναδικό όριο µιας συνάρτησης f,
για x →+∞ (αντίστοιχα για x →−∞), µε το σύµβολο lim f ( x)
(αντίστοιχα µε το
lim f ( x)
).
x→−∞
x→+∞
5.2.4 Θεώρηµα
Υποθέτουµε ότι οι συναρτήσεις f και g έχουν κοινό πεδίο ορισµού Α. Τότε ισχύουν τα εξής:
i) lim c= lim c= c, όπου c∈ .
x→+∞
x→−∞
ii) Αν lim f ( x)
= a τότε lim | f ( x) | = | a|
. Αντίστοιχα, αν lim f ( x)
= a,
x→+∞
τότε lim | f ( x) | = | a|
.
x→−∞
x→+∞
x→−∞
iii) Αν lim f ( x)
= a και λ ∈ , τότε lim ( λ f ( x))
= λa. Αντίστοιχα,
x→+∞
x→+∞
αν lim f ( x)
= a και λ ∈ , τότε lim ( λ f ( x))
= λa.
x→−∞
x→−∞
iv) Αν lim f ( x)
= a και lim g( x)
= b, τότε lim( f ( x) + g( x))
= a+ b.
x→+∞
x→+∞
x→+∞
Αντίστοιχα, αν lim f ( x)
= a και lim g( x)
= b, τότε lim( f( x) + g( x))
= a+ b.
x→−∞
x→−∞
x→−∞
v) Αν lim f ( x)
= a και lim g( x)
= b, τότε lim ( f ( xgx ) ( )) = ab ⋅ .
x→+∞
x→+∞
x→+∞
Αντίστοιχα, αν lim f ( x)
= a και lim g( x)
= b, τότε lim ( f ( xgx ) ( )) = ab ⋅ .
x→−∞
x→−∞
x→−∞
vi) Αν lim f ( x)
= a, lim g( x)
= b, gx≠ ( ) 0 για κάθε x∈ A και b ≠ 0 ,
τότε
x→+∞
x→+∞
f ( x)
a
= . Αντίστοιχα, αν lim f ( x)
= a, lim g( x)
= b, gx≠ ( ) 0 για κάθε
xlim
→+∞ g ( x ) b
x→−∞
x→−∞
x∈ A και b ≠ 0 , τότε
lim f ( x)
a
= .
x→−∞
g ( x ) b
vii) Αν f( x) ≥ 0 για κάθε x∈ A και lim f ( x)
x→+∞
Αντίστοιχα, αν lim f ( x)
= a, lim
k
k
f ( x)
= a . ■
x→−∞
x→−∞
= a, τότε lim
k
k
f ( x)
= a .
x→+∞

28
5.2.5 Παράδειγµα
1
Θεωρούµε τη συνάρτηση µε τύπο f( x)
= . Τότε lim f( x) = lim f( x) = 0 . Πράγµατι, αν
x
x→+∞
x→−∞
1
1
1
ε > 0 , τότε η σχέση 0 < < ε είναι ισοδύναµη µε τη σχέση x > . Αν θέσουµε δ = , τότε
x
ε
ε
1
1
για κάθε x∈
( δ , +∞ ) έχουµε 0 < < ε . Άρα lim = 0 .
x
x→+∞
x
f(x) =
1
x
-∞
Ο
+∞
1
Η σχέση πάλι − ε < < 0 είναι ισοδύναµη µε τη σχέση
x
1
παίρνουµε − ε < < 0 , για κάθε x∈−∞− ( , δ ).
x
1
1
x < − . Και εδώ θέτουµε δ = και
ε
ε
5.2.6 Πρόταση
Θεωρούµε µια ρητή συνάρτηση µε τύπο
n
ax
n
+ a x + + ax+
a
f( x)
=
n
bx + b x + + bx+
b
n
n−1
n−1 1 0
n−1
n−1
1 0
, όπου bn
≠ 0 .
∆ηλαδή,
υποθέτουµε ότι ο παρονοµαστής έχει βαθµό µεγαλύτερο ή ίσο του βαθµού του
αριθµητή.
an
Τότε lim f( x) = lim f( x) = .
x→+∞
x→−∞
b
n
Απόδειξη: Παρατηρούµε ότι, για κάθε x ≠ 0 , έχουµε
n 1 1 1
n n−1 x ( an + an 1
a1 a
1 0
)
ax n n
n
an
1x ax
1
a
−
+ + +
+ −
−
+ + +
0
f( x)
= = x x x =
n
n−1
bx 1 1 1
n
+ bn−
1x + + bx
1
+ b0
n
x ( bn + bn−
1
+ + b1 + b
1 0
)
n−
n
x x x
1 1 1
an + an−
1
+ + a1 + a
n−1
0 n
= x x x .
1 1 1
bn + bn−
1
+ + b1 + b
n−1
0 n
x x x

29
1 1
Έχουµε ήδη δείξει (παράδειγµα 5.2.5) ότι lim = lim = 0 . Από το v) του θεωρήµατος
x→+∞
x x→−∞
x
1 1
5.2.4 προκύπτει ότι lim = lim = 0 για κάθε θετικό ακέραιο k.
x→+∞
k
x
k
x →−∞ x
1 1 1
Εποµένως, lim = lim = = lim = 0 .
x→±∞ x
n−1
x
n
x →±∞ x →±∞ x
1 1 1
an + an−
1
lim + + a1 lim + a
1 0
lim
x→±∞ x
n
x
n
n
Άρα, lim ( )
x →±∞
−
x →±∞ a
f x =
x
= , σύµφωνα και µε τα iii),
x→±∞
1 1 1
b
1
lim
1
lim
1 0
lim
bn
n
+ bn−
+ + b + b
x→±∞ x
n−
x
n
x →±∞ x →±∞ x
iv) και vi) του θεωρήµατος 5.2.4. ■
5.2.7 Παραδείγµατα
2
4 2
x − x+
3
1. Να βρεθούν τα όρια: i) lim
x→−∞
3 2
x + 2x + x− 1
, ii) lim − 3x
+ 3x
−6
x→+∞
2
4 3 2
x + x −x
− . 1
2 3 2
x − x+ 3 0⋅ x + x − x+
3 0
Λύση: i) lim = lim = = 0 , σύµφωνα µε την προηγούµενη
x→−∞
3 2 3 2
x + 2x + x− 1 x→−∞
x + 2x + x−1 1
πρόταση.
4 2
ii) lim − 3x
+ 3x
−6 3
=− , σύµφωνα µε την προηγούµενη πρόταση.
x→+∞
2
4 3 2
x + x −x
− 1 2
2. Να βρεθούν τα όρια: i) lim ( x )
2 + x+ 3 − x+ 1 , ii) lim ( x )
2 2x 4 x 3
iii) lim
x→+∞
x − x
, iv) lim
x − 2 x→−∞
x→+∞
2
x + 3
, v)
x − 4
2
Λύση: i) ( x x x )
x
2
lim
x→−∞
9
2
x 1
+ 2 − x
+ + x
.
( ) 2
x→−∞
+ + + − ,
x 2 + x+ 3 −( x−1)
2
lim + + 3 − + 1 = lim
=
x→+∞
x→+∞
2
x + x+ 3+ x−1
2 2
x + x+ 3− x + 2x− 1 3x+
2
lim
= lim
. Εφόσον x →+∞, µπορούµε να
x→+∞
2 x→+∞
2
x + x+ 3+ x− 1 x + x+ 3+ x− 1
υποθέσουµε ότι x > 0 . Εποµένως,
⎛ 2 ⎞
x 3 +
2
3 +
3x + 2
⎜ ⎟
x
lim = lim
⎝ ⎠
= lim x =
x→+∞ 2
x→+∞ x→+∞
x + x+ 3+ x−1
⎛ 1 3 1⎞
1 3 1
x⎜
1+ + + 1−
1 1
2 ⎟ + + + −
2
⎝ x x x⎠
x x x
2
3+
lim
x→+∞
x
3+
0 3
= = = .
1 3 1 1+ 0+ 0 + 1−0
2
1+ lim + lim + 1−
lim
x→+∞ x
2
x →+∞ x x→+∞
x
2 2
2
x + 2x+ 4 −( x−3)
8x
− 5
ii) lim ( x + 2x+ 4 + x− 3)
= lim
= lim .
x→−∞
x→−∞
2
x→−∞
2
x + 2x+ 4 −( x−3)
x + 2x+ 4 − x+
3
Εφόσον x →−∞, µπορούµε να υποθέσουµε ότι x < 0 .

30
8x−5 8x−5
Εποµένως, lim
= lim
=
x→−∞
2
x→−∞
x + 2x+ 4 − x+
3
2 4
| x| 1+ + − x+
3
2
x x
⎛ 5 ⎞
x 8 −
5
8 −
8x − 5
⎜ ⎟
x
lim = lim
⎝ ⎠
= lim x =
x→−∞ 2 4
x→−∞ ⎛
x
2 4 3⎞
→−∞
2 4 3
− x 1+ + − x+ 3 1 1
2
x⎜− 1+ + − 1+
2 ⎟ − + + − +
2
x x
⎝ x x x⎠
x x x
5
8−
lim
x→−∞
x
8−
0
= = =−4
.
2 4 3 − 1+ 0+ 0 − 1+
0
− 1+ lim + lim − 1+
lim
x→−∞ x
2
x →−∞ x x→−∞
x
⎛ 1 ⎞ 1
x −1 1
−1 lim −1
x −x ⎜ ⎟
x x
0 1
iii) lim lim lim
x →+∞ x −
=
⎝ ⎠
= = = =−1
.
x→+∞ x −2 x→+∞ ⎛ 2 ⎞ x→+∞
2 2
1 1 lim
1−0
x⎜1−
⎟ − −
x
x
x→+∞
⎝ ⎠
x
3 3
2 | x | 1+ 1+
2 2
x + 3 1 0
iv) lim lim
x
lim
x +
= =− =− =−1
.
x→−∞ x −4 x→−∞ ⎛ 4 ⎞ x< 0 x→−∞
4
1
1−0
x⎜1−
⎟
−
⎝ x ⎠
x
2 2
2 | x | 1+ −x − x 1+ −x
2 2
x + 2 −x v) lim = lim
x
= lim
x
=
x→−∞ 2 x→−∞ 1
x< 0 x→−∞
9x
+ 1+
x
1
| x | 9+ + x − x 9+ + x
2 2
x
x
2
− 1+ −1
2
1 0 1
lim
x − + −
= = = 1 .
x→−∞
1 − 9+ 0 + 1
− 9+ + 1
2
x
2
⎛ x − 3x+ 1 ⎞
3. Να βρεθούν τα ab∈R , , ώστε lim ⎜ − ax − b⎟
= 0 .
x→+∞
⎝ 2x
−1
⎠
2
⎛ x 3 1
Λύση: Εφόσον lim − x + 2
⎞
⎜ − ax − b⎟
= 0 και
x→+∞
⎝ 2x
−1
lim ⎛ x − 3x+ 1 b⎞
⎜
a
x→+∞
2 − − ⎟ =
⎠
⎝ 2 x − x x⎠
2
⎛1⎛
x − 3x+
1 ⎞⎞
= lim ax b 0
x→+∞⎜
⎜ − − ⎟
=
x 2x−1
⎟
.
⎝ ⎝
⎠⎠
2 2
⎛ x − 3x+ 1 b⎞
x − 3x+
1 b 1
Άρα 0 = lim ⎜ −a− lim a lim a
x
2 ⎟= − − = −
→+∞
2
2x x x x→+∞ 2x x x→+∞
⎝ − ⎠
−
x 2
1
a = .
2
2 2
⎛ x − 3x+ 1 1 ⎞ ⎛ x − 3x+
1 1 ⎞
Τώρα, lim ⎜ − x − b⎟= 0 ⇔ b= lim ⎜ − x⎟=
x→+∞
2x
1 2 x→+∞
⎝ −
⎠ ⎝ 2x−1 2 ⎠
2
2x − 6x+ 2 −x(2x−1) − 5x+
2 5
= lim
= lim =− .
x→+∞
2(2x−1) x→+∞
4x−2 4
Η γεωµετρική ερµηνεία του παραπάνω γεγονότος είναι η ακόλουθη:
και εποµένως,

31
2
x − 3x+
1
Η απόσταση ενός σηµείου της γραφικής παράστασης της συνάρτησης y = από το
2x
−1
1 5
σηµείο της ευθείας y = x− που βρίσκεται στην ίδια κατακόρυφη µε αυτό τείνει στο
2 4
µηδέν, καθώς το x →+∞.
y
y= 1 2 x 5
4
O
x
διαφορά
y=
x 2 -3x+1
2x-1
1 5
Λέµε ότι η ευθεία y= x− είναι µια πλάγια ασύπτωτη της γραφικής παράστασης της
2 4
2
x − 3x+
1
συνάρτησης y = . Έχουµε λοιπόν τον επόµενο ορισµό:
2x
−1
5.2.8 Ορισµός
Θεωρούµε µια συνάρτηση f :
( δ , +∞ ) ή της µορφής ( −∞, − δ ), όπου δ > 0 .
A→ R . Υποθέτουµε ότι το Α περιέχει ένα διάστηµα της µορφής
i) Αν το όριο lim [ f ( x) −ax− b]
ή το όριο lim [ f ( x) − ax− b]
υπάρχει και είναι µηδέν, τότε η
x→+∞
x→−∞
ευθεία y = ax+ b λέγεται πλάγια ασύπτωτη της γραφικής παράστασης της f. Αν a = 0 η
ευθεία y = b λέγεται οριζόντια ασύµπτωτη της γραφικής παράστασης της f.
ii) Αν x0
∈R είναι ένα σηµείο συσσώρευσης του Α και
lim f( x)
= ±∞ , τότε η ευθεία x = x0
x→x
±
0
λέγεται κάθετη ασύµπτωτη της γραφικής παράστασης της f.
5.2.9 Παρατηρήσεις
i) Ακολουθώντας τη µέθοδο του προηγουµένου παραδείγµατος, µπορεί να δείξει κανείς ότι οι
f ( x)
αριθµοί ab∈R , ορίζονται µονοσήµαντα ως εξής: a = lim και b= lim [ f( x) − ax]
.
x→±∞
x
x→±∞
π
ii) Στο παράδειγµα 5.1.21.2) δείξαµε ότι lim tan x = ∓ ∞ . Άρα οι ευθείες x= kπ
+
π
±
⎛ ⎞
2
x→ ⎜kπ
+ ⎟
⎝ 2 ⎠
είναι κάθετες ασύµπτωτες της γραφικής παράστασης της συνάρτησης
y = tan x.

32
5.2.10 Παραδείγµατα
1. Να βρεθούν όλες οι ασύµπτωτες της γραφικής παράστασης της συνάρτησης
2
x − 3x+
1
y = .
2x
−1
1 5
Λύση: Έχουµε ήδη βρει µια ασύµπτωτη, την y = x− . Παίρνουµε τώρα τα όρια για
2 4
2
2
⎛1 x − 3x+
1⎞
1 ⎛ x − 3x+ 1 1 ⎞ 5
x →−∞: lim ⎜
⎟=
και lim ⎜ − x⎟
=− . Καταλήγουµε στην
x→−∞
⎝ x 2x−1 ⎠ 2 x→−∞
⎝ 2x
−1 2 ⎠ 4
ίδια ευθεία.
Η συνάρτησή µας έχει πεδίο ορισµού το R {}. 1 Ενδεχοµένως λοιπόν να απειρίζεται στο
2
1
σηµείο x = .
2
Παρατηρούµε ότι
lim
x→(1/ 2)
−
1
= 0 µε 2x − 1< 0, για x < .
Ανάλογα βρίσκουµε ότι
ευθείες
1 5
y= x− και
2 4
2
x − 3x+ 1 = +∞
2x
−1
2
lim
x→(1/ 2)
+
1
x = .
2
1
, γιατί ( ) 2 1 1
− 3⋅ + 1=− < 0 και lim ( 2x
1)
2 2 4
x→(1/ 2)
−
− =
2
x − 3x+ 1 = −∞ . Οι ζητούµενες ασύµπτωτες είναι λοιπόν οι
2x
−1
y
y= 1 2 x 5
4
O
1
2
y=
x 2 -3x+1
2x-1
2. Να βρεθούν όλες οι ασύµπτωτες της γραφικής παράστασης της συνάρτησης
2
2x
− x + 1
y = .
2
x −x−2
Λύση: Το πεδίο ορισµού της συνάρτησης είναι το
R
2
{ x∈ | x −x−2≠0}
. Οι ρίζες της
εξίσωσης
x
2
−x− 2= 0 είναι το -1 και το 2. Είναι
2
x x x x
− − 2 = ( + 1)( − 2) . Είναι
2
x x x x
− − 2> 0⇔ 2 και
Έχουµε
2
x x x
− − 2< 0⇔ − 1< < 2.
2 2 2
lim (2x x 1) lim (2x x 1) 2 1 1 1 4 0
x→−1 −
x→−1
+
− + = − + = ⋅ + + = > και

33
2 2 2
lim (2x x 1) lim (2x x 1) 2 2 2 1 7 0
x→2 −
x→2
+
2
2
2x
x 1
2x
x 1
Εποµένως,
lim
x→2
+
− + = − + = ⋅ − + = > .
lim
x→−1
−
2
2x
x 1
x
2
x
− + =+∞ .
−x−2
2
− + =+∞ ,
−x−2
lim
x→−1
+
x
2
− + = −∞ ,
−x−2
lim
x→2
−
2
2x
x 1
x
2
− + =−∞
−x−2
και
Οι ευθείες x =− 1 και x = 2 είναι οι κάθετες ασύµπτωτες.
2
y 2x − x+
1
= →0
για x →±∞. Άρα έχουµε οριζόντιες ασύµπτωτες. ( a = 0 )
3 2
x x −x −2x
2
2x
− x+
1
b = lim = 2 . Η οριζόντια ασύµπτωτη είναι η ευθεία y = 2.
x→±∞
2
x −x−2
y
2
-1
O
2
x
y =
2x2 -x+1
x 2 -x-2
Άλυτες ασκήσεις
3
3 2
− 2x
+ x
1. Να υπολογιστoύν τα όρια: (i) lim
x→+∞
3 2
x − 3x + x+ 1
, (ii) ⎛ x x ⎞
lim ⎜ −
x
2 ⎟,
→+∞
⎝2x
−1
2x
+ 1⎠
2
2 2
x− x + 1
x + 1−1
(iii) lim ( x + a − x)
, (iv) lim ( x + 1 − x − 1)
, (v) lim
, (vi) lim .
x→+∞
x→−∞
x→−∞
2
x→+∞
2
x−
x −1
x − x
2004 2004 2004 2004
( x+ 1) + ( x+ 2) + ( x+ 3) + + ( x+
2004)
2. ∆είξτε ότι: lim = 2004 .
x→+∞
2004 2004
x + 2004
2004
(Υπόδειξη: ∆ιαιρέστε αριθµητή και παρονοµαστή µε το x ).
2x
+ 1
3. Να βρεθούν οι ασύµπτωτες των γραφικών παραστάσεων των συναρτήσεων: (i) f( x)
=
2
x −x− 2
,
2 2
2 x− | x+
1|
(ii) gx ( ) = x − 2x+ 3− x + 3 , και (iii) hx ( ) = .
x
Όπως στα όρια για x→
x0
∈R , έτσι και δω ισχύει το κριτήριο της παρεµβολής. Η απόδειξή
του είναι παρόµοια µε αυτήν της µορφής 5.1.12 και, γι’ αυτό παραλείπεται.

34
5.2.11 Πρόταση (κριτήριο παρεµβολής)
i) Έστω f ( x) ≤h( x) ≤ g( x)
για κάθε x∈ ( δ , +∞)
∩ A, όπου δ > 0 .
Αν lim f( x) = lim g( x)
= a∈R , τότε και lim hx ( ) = a.
x→+∞
x→+∞
x→+∞
ii) Έστω f ( x) ≤h( x) ≤ g( x)
για κάθε A ∩ ( −∞, − δ ), όπου δ > 0 .
Αν lim f( x) = lim g( x)
= a∈R , τότε και lim hx ( ) = a. ■
x→+∞
x→+∞
x→+∞
5.2.12 Παράδειγµα
sin x
2x
+ sinx
Να βρεθούν τα όρια: i) lim και ii) lim .
x→±∞
2
x
x→+∞
x + 3
sin x 1 1 sin x 1
⎛ 1 ⎞ 1
Λύση: i) ≤ ⇔− ≤ ≤ για κάθε x ≠ 0. Ακόµη, lim ⎜− ⎟= lim =
x | x| | x| x | x|
x→±∞
| x | x→±∞
⎝ ⎠ | x |
sin x
= 0 . Άρα lim = 0 .
x→±∞
x
2x+ sin x 2x + sin x 2x
+ 1
ii) 0 ≤ ≤ ≤
2 2 2
x + 3 x + 3 x + 3
, εφόσον x > 0 και 2x
+ 1
lim 0
x
2 = .
→+∞ x + 3
2x+
sinx
Άρα lim = 0 .
x→+∞
2
x + 3
Άλυτες ασκήσεις
1. ∆ίνεται η συνάρτηση f :(0, +∞)
→R , για την οποία ισχύει η σχέση:
κάθε x > 0 . Να υπολογιστεί το lim f( x)
.
x→+∞
2 2
|(2 1) ( ) |
x + f x −x ≤ x , για
Τέλος, θα ασχοληθούµε µε τα απειριζόµενα όρια, για x →±∞. ∆εν έχουµε παρά να
τροποποιήσουµε τον ορισµό 5.1.19.
5.2.13 Ορισµός
Έστω f :
A→ R µια συνάρτηση.
i) Υποθέτουµε ότι, για κάθε δ > 0 , το Α περιέχει ένα τουλάχιστον στοιχείο του διαστήµατος
( δ , +∞ ).
Θα λέµε ότι η συνάρτηση f συγκλίνει, για x →+∞, στο +∞ αν, για κάθε ε > 0
(οσοδήποτε µεγάλο) υπάρχει δ > 0 µε την ιδιότητα:
Αν x∈A∩ ( δ , +∞ ) τότε f( x)
> ε .

35
Γράφουµε lim f( x)
= +∞ .
x→+∞
Θα λέµε ότι η συνάρτηση f συγκλίνει, για x →+∞, στο −∞ αν, για κάθε ε > 0
(οσοδήποτε µεγάλο) υπάρχει δ > 0 µε την ιδιότητα:
Γράφουµε lim f( x)
= −∞ .
x→+∞
Αν x∈A∩ ( δ , +∞ ) τότε f( x)
< − ε .
ii) Υποθέτουµε ότι, για κάθε δ > 0 , το Α περιέχει ένα τουλάχιστον στοιχείο του διαστήµατος
( −∞, − δ ).
Θα λέµε ότι η συνάρτηση f συγκλίνει, για x →−∞, στο +∞ αν, για κάθε ε > 0
(οσοδήποτε µεγάλο) υπάρχει δ > 0 µε την ιδιότητα:
Γράφουµε lim f( x)
= +∞ .
x→−∞
Αν x∈A∩( −∞, − δ ) τότε f( x)
> ε .
Θα λέµε ότι η συνάρτηση f συγκλίνει, για x →−∞, στο −∞ αν, για κάθε ε > 0
(οσοδήποτε µεγάλο) υπάρχει δ > 0 µε την ιδιότητα:
Γράφουµε lim f( x)
= −∞ .
x→−∞
Αν x∈A∩( −∞, − δ ) τότε f( x)
< − ε .
Είναι προφανές ότι, µε ορισµένες τροποποιήσεις, µπορεί κανείς εύκολα να επαληθεύσει
αποτελέσµατα αντίστοιχα µε αυτά της πρότασης 5.1.20.
∆ιατυπώνουµε την αντίστοιχη πρόταση:
5.2.14 Πρόταση
Έστω f, g:
A→ R συναρτήσεις. Υποθέτουµε ότι, για κάθε δ > 0 , το Α περιέχει ένα
τουλάχιστον σηµείο του διαστήµατος ( δ , + ∞ ). Ισχύουν τα εξής:
i) Αν f ( x) ≤ g( x)
για κάθε x∈ A και lim f( x)
= +∞ , τότε lim gx ( ) = +∞ .
x→+∞
x→+∞
ii) Αν f ( x) ≤ g( x)
για κάθε x∈ A και lim gx ( ) = −∞ , τότε lim f( x)
= −∞ .
x→+∞
iii) Αν lim f( x)
= a∈R ή lim f( x)
= +∞ και lim gx ( ) = +∞ ,
x→+∞
x→+∞
τότε lim[ f( x) + g( x)]
=+∞.
x→+∞
x→+∞
iv) Αν lim f( x)
= a∈R ή lim f( x)
= −∞ και lim gx ( ) = −∞ ,
x→+∞
x→−∞
τότε lim[ f( x) + g( x)]
=−∞.
x→+∞
x→+∞
x→−∞
v) Αν lim f( x)
= a∈R µε a > 0 και lim gx ( ) = +∞ , τότε lim[ f( x) g( x)]
=+∞.
x→+∞
x→+∞
x→+∞
Αν lim f( x)
= a∈R µε a > 0 και lim gx ( ) = −∞ , τότε lim[ f( x) g( x)]
=−∞.
x→+∞
x→+∞
x→+∞

36
vi) Αν lim f( x)
= a∈R µε a < 0 και lim gx ( ) = +∞ , τότε lim[ f( x) g( x)]
=−∞.
x→+∞
x→+∞
x→+∞
Αν lim f( x)
= a∈R µε a < 0 και lim gx ( ) = −∞ , τότε lim[ f( x) g( x)]
=+∞.
x→+∞
x→+∞
x→+∞
vii) Αν lim f( x) = lim g( x)
=+∞ ή lim f( x) = lim g( x)
=−∞,
x→+∞
x→+∞
τότε lim[ f( x) g( x)]
=+∞.
x→+∞
x→+∞
x→+∞
Αν lim f( x)
= +∞ και lim gx ( ) = −∞ , τότε lim[ f( x) g( x)]
= −∞ .
x→+∞
x→+∞
viii) Αν lim f( x)
= +∞ ή lim f( x)
= −∞ , τότε
x→+∞
x→−∞
x→+∞
1
lim = 0 .
x→+∞
f( x)
ix) Αν lim f( x) = 0 και f( x ) > 0 για κάθε x∈ A , τότε
x→+∞
1
lim = +∞ .
x→+∞
f ( x )
Αν lim f( x) = 0 και f( x ) < 0 για κάθε x∈ A , τότε lim 1
= −∞ .
x→+∞
x→+∞
f ( x )
x) Αν f( x) ≥ 0 για κάθε x∈ A και lim f( x)
= +∞ τότε lim
k
f( x)
= +∞ ,
όπου k θετικός ακέραιος.
x→+∞
x→+∞
Όλα τα παραπάνω ισχύουν και για x →−∞, αντί x →+∞, µε την προϋπόθεση ότι, για κάθε
δ > 0 , το Α περιέχει ένα τουλάχιστον σηµείο του διαστήµατος ( −∞, − δ ). ■
5.2.15 Παραδείγµατα
1. Έστω k θετικός ακέραιος. Εφόσον lim x = +∞ , τότε, µε επαγωγή επί του k και
x →+∞
εφαρµόζοντας το (vii) της προηγούµενης πρότασης, καταλήγουµε στο συµπέρασµα ότι
lim x
k =+∞.
x→+∞
Για x →−∞, ακολουθούµε την ίδια µέθοδο και συµπεραίνουµε ότι:
i) k άρτιος: Τότε lim x
k = +∞ .
x→−∞
ii) k περιττός: Τότε lim x
k = −∞ .
2. Έστω f ( x ) =
x→−∞
m
m−1
amx + am−
1x + + a1x+
a0
n
n−1
bx
n
+ bn−
1x + + bx
1
+ b0
ρητή συνάρτηση µε m> n και a , b ≠ 0.
m
n
Τότε
Αλλά,
⎛ 1 1 1 ⎞
x a + a + + a + a
a x + a x + + a x+ a
⎟
x x x
lim
⎝ ⎠
.
x→+∞
m−n
m m−1 m m−1 1 m−1
0 m
m m−1
⎜
1 0
= lim
n
n−1
bx x
1 1 1
n
+ bn
1x bx
1
b →+∞
−
+ + +
0
bn + bn−
1
+ + b1 + b
n−1
0 n
1 1 1
a + a + + a + a
lim x x x
x→+∞
1 1 1
bn + bn−
1
+ + b1 + b
n−1
0 n
x x x
m m−1 1 m−1
0 m
a
=
b
m
n
και lim
x m−n
x→+∞
x x x
= +∞ .
Με βάση τα (v) και (vi) της πρότασης 5.2.14,
m
m−1
a , αν τα και είναι οµόσηµοι
mx + a a
1 1 0
m
b
m−
x + + a x+
a ⎧+∞
n
lim
=
x
n
n−1
⎨
→+∞ bx
n + bn−
1x + + bx
1 + b0
⎩ −∞ , αν τα am
και bn
είναι ετερόσηµοι

37
Ειδικά για πολυωνυµικές συναρτήσεις
, αν a 0
m
m−1
⎧+∞
m
>
lim ( amx + am−
1x + + a1x+ a0)
=⎨
x→+∞
⎩ −∞ , αν am
< 0
Για x →−∞ διακρίνουµε δύο περιπτώσεις:
i) m-n άρτιος:
m
m−1
a , αν τα και είναι οµόσηµοι
mx + a a
1 1 0
m
b
m−
x + + a x+
a ⎧+∞
n
lim
=
x
n
n−1
⎨
→−∞ bx
n + bn−
1x + + bx
1 + b0
⎩ −∞ , αν τα am
και bn
είναι ετερόσηµοι
Ειδικά για πολυωνυµικές συναρτήσεις
, αν a 0
m
m−1
⎧+∞
m
>
lim ( amx + am−
1x + + a1x+ a0)
=⎨
x→−∞
⎩ −∞ , αν am
< 0
ii)
m-n περιττός:
m
m−1
a , αν τα και είναι οµόσηµοι
mx + a a
1 1 0
m
b
m−
x + + a x+
a ⎧−∞
n
lim
=
x
n
n−1
⎨
→−∞ bx
n + bn−
1x + + bx
1 + b0
⎩ +∞ , αν τα am
και bn
είναι ετερόσηµοι
Ειδικά για πολυωνυµικές συναρτήσεις
, αν a 0
m
m−1
⎧+∞
m
<
lim ( amx + am−
1x + + a1x+ a0)
=⎨
x→−∞
⎩ −∞ , αν am
> 0
3. Να βρεθούν τα όρια: i) lim ( x+ x )
2 + x− 1 , ii) lim ( 2x x )
2 x 1
x→+∞
x→+∞
iii) lim ( 2x+ x )
2 − x+ 1 .
x→−∞
2
Λύση: i) Έχουµε lim ( x x 1)
lim
2
x x 1
x→+∞
x→+∞
− − + και
+ − =+∞, σύµφωνα µε το προηγούµενο παράδειγµα. Άρα
+ − =+∞, σύµφωνα µε το (x) της πρότασης 5.2.14. Επίσης, lim x =+∞ και
x →+∞
εποµένως, σύµφωνα µε το (iii) της ίδιας πρότασης παίρνουµε lim ( x x )
2 x 1
⎡ ⎛ 1 1 ⎞⎤
lim 2x− x − x+ 1 = lim ⎢x
2 1
x→+∞
x→+∞
⎜
− − +
2
⎥
x x ⎟
.
⎢⎣
⎝
⎠⎥⎦
⎛ 1 1 ⎞
Ακόµη, lim 2 1 2 1 1 0
x→+∞⎜
− − + = − = >
2
x x ⎟
και lim x = +∞ .
x →+∞
⎝
⎠
2
ii) ( )
x→+∞
+ + − =+∞.
⎡ ⎛ 1 1 ⎞⎤
Άρα lim ⎢x
2 1
x→+∞
⎜
− − + =+∞
2
⎥
x x ⎟
(πρόταση 5.2.14 (v)).
⎢⎣
⎝
⎠⎥⎦
⎛
2
1 1 ⎞ ⎛ 1 1 ⎞
iii) lim ( 2x+ x − x+ 1)
= lim 2 x | x| 1 lim 2x x 1
x→−∞ x→−∞ ⎜
+ − +
2 x 0 x
2
x x ⎟
= − − + =
< →−∞⎜ x x ⎟
⎝ ⎠ ⎝ ⎠
⎡ ⎛ 1 1 ⎞⎤
⎛ 1 1 ⎞
= lim ⎢x
2 − 1− +
x→−∞
⎜
2
⎥
x x ⎟
, lim 2 1 1 0
x→−∞⎜
− − +
2
= >
⎢⎣
⎝
⎠⎥⎦
x x ⎟
και lim x = −∞ .
x →−∞
⎝
⎠
⎡ ⎛ 1 1 ⎞⎤
Άρα lim ⎢x
2 1
x→−∞
⎜
− − + =−∞
2
⎥
x x ⎟
(πρόταση 5.2.14 (v)).
⎢⎣
⎝
⎠⎥⎦

38
Άλυτες ασκήσεις
3
5 1
1. Να υπολογιστούν τα όρια: (i) lim x −
, (ii) lim
x→−∞
| x + 1| x→+∞
2
− 3x
+ 7x+
2
(iv) lim
, (v) lim
x→−∞
2
x→+∞
x + 2x+
4
2
−x
− x+
3 1
.
2
x − 2x−
4
2
| x − 3 x| + 5
x − 3
, (iii)
2. Να υπολογιστούν τα όρια lim ( x )
2 + x+ 1 − ax και lim ( x )
2 x 1 ax
του a ∈ R .
x→−∞
x→+∞
lim
2
3x
2x
1
x→−∞
− − ,
+ + − για τις διάφορες τιµές
Κλείνουµε την παράγραφο αυτή µε ένα αποτέλεσµα, το οποίο είναι γενίκευση της πρότασης
5.1.14. Για να το διατυπώσουµε χρειαζόµαστε κάποιους συµβολισµούς.
5.2.16 Συµβολισµοί*
Έστω x ∈R . Αν ε > 0, τότε θέτουµε sx ( , ε ) = ( x− ε, x+ ε)
.
Ακόµη, θέτουµε s( +∞ , ε) = ( ε,
+∞ ) και s( , ε ) ( , ε )
−∞ = −∞ − .
Μπορεί κανείς να ελέγξει ότι, όλοι οι ορισµοί που δώσαµε για τα όρια συναρτήσεων µπορούν
να διατυπωθούν κατά ενιαίο τρόπο ως εξής:
Έστω f : A→ R µια συνάρτηση και ab∈ , R ∪{ −∞ , +∞}
. Υποθέτουµε ότι για κάθε δ > 0
το σύνολο A
( a )
{} ∩ s(, a δ ) δεν είναι κενό.
Τότε lim f ( x ) = b αν και µόνον αν για κάθε ε > 0 υπάρχει δ > 0 τέτοιο ώστε,
x→a f ( x) ∈ s( b, ε ), για κάθε x A
∈( a )
{} ∩ s(, a δ ).
Πράγµατι, αν ab∈R , , η σχέση x∈( A {} a ) ∩ s(, a δ ) είναι ισοδύναµη µε τη συνθήκη:
x∈ A και 0 < | x− a|
< δ . Επίσης, η σχέση f ( x) ∈ s( b, ε ) είναι ισοδύναµη µε την
| f( x) − b|
< ε .
Αν a ∈R και b =+∞, η σχέση f ( x) ∈ s( b, ε ) είναι ισοδύναµη µε την f( x)
> ε .
Για x →−∞, η σχέση x A {} a ∩ s(, a δ ) είναι ισοδύναµη µε τη συνθήκη: x∈ A και
∈( )
x 0 .
x→a

39
(ii) lim f ( u ) = c .
u→b Τότε lim f ( gx ( )) = c .
x→a *Απόδειξη: Έστω ε > 0. Εφόσον lim f ( u ) = c , υπάρχει δ ′ > 0 µε την ιδιότητα:
u→b u∈( B {} b ) ∩s(, b δ ′) ⇒ f( u) ∈ s(, c ε ). (1)
Εφόσον lim g ( x ) = b , υπάρχει δ ′′ > 0 µε την ιδιότητα:
x→a x∈( A {} a ) ∩s(, a δ ′′) ⇒ g() x ∈ s(, b δ ′).
Μπορούµε να υποθέσουµε ότι δ ′′ < δ , οπότε
x∈( A {} a ) s(, a δ ′′) g()
x B
∩ ⇒ ∈( )
{} b ∩ s(, b δ ′). (2)
Αν συνδυάσουµε τις σχέσεις (1) και (2) θα πάρουµε
x A {} a ∩ s(, a δ ′′)
⇒ f ( gx ( )) ∈ scε ( , ). ■
∈( )
5.2.18 Παράδειγµα
⎛ ⎛1
⎞⎞
Να υπολογιστεί το lim ⎜xsin
⎜ ⎟⎟
x→+∞⎝ ⎝ x ⎠⎠ Λύση:
⎛1
⎞
sin
⎛ 1
⎜ ⎟
⎛ ⎞⎞
x
lim xsin lim
⎝ ⎠
1
⎜ ⎜ ⎟⎟=
. Θέτουµε u = = g( x)
.
x→+∞
x x→+∞
⎝ ⎝ ⎠⎠
1
x
Παρατηρούµε ότι
x
1
1 sinu
lim gx ( ) = lim = 0 . Εφαρµόζουµε την προηγούµενη πρόταση µε gx ( ) = , f( u)
= ,
x→+∞
x→+∞
x
x u
⎛ ⎛1⎞⎞
sinu
a =+∞ και b = 0. Έχουµε λοιπόν lim ⎜xsin ⎜ ⎟⎟
= lim = 1.
x→+∞ x u> 0 u→0
+
⎝ ⎝ ⎠⎠
u

40
5.3 Συνεχείς συναρτήσεις
Στα επόµενα σχήµατα παριστάνονται οι γραφικές παραστάσεις τεσσάρων συναρτήσεων.
y
y
g(x 0 )
f(x 0 )
lim x→ x0
g(x 0 )
a
O
x 0
b
x
a
O
x 0
b
x
y
y
h(x 0 )
r(x 0 )
a O x 0
b x
a O x 0
b x
Παρατηρούµε ότι οι συναρτήσεις g, h και r παρουσιάζουν ιδιοµορφία στο σηµείο x
0
. Η
γραφική τους παράσταση φαίνεται να «διακόπτεται» στο σηµείο αυτό. Η g παρουσιάζει µια
οπή στη γραφική της παράσταση. Υπάρχει το
lim g ( x )
x x
→ 0
αλλά αυτό δεν είναι ίσο µε το gx (
0)
.
Στις περιπτώσεις των h και r, παρατηρούµε ουσιωδέστερη διαταραχή στη γραφική
παράσταση. Σ’ αυτές τις περιπτώσεις δεν υπάρχει ούτε το όριο της συνάρτησης στο x
0
. ( Η h
έχει δύο διαφορετικά πεπερασµένα πλευρικά όρια ενώ η r έχει ένα πεπερασµένο αριστερό και
ένα απειριζόµενο δεξιό πλευρικό όριο). Λέµε ότι οι συναρτήσεις g, h και r είναι ασυνεχείς
στο x
0
ενώ, η f είναι συνεχής στο σηµείο αυτό.
5.3.1 Ορισµός
Θεωρούµε µια συνάρτηση f : A→ R και x
0
ένα σηµείο του πεδίου ορισµού της Α.
i) Αν το x
0
είναι σηµείο συσσωρεύσεως του Α τότε, λέµε ότι η f είναι συνεχής στο x
0
αν
υπάρχει το lim f ( x)
και ισούται µε την τιµή f ( x
0)
της f στο x
0
.
x→x0

41
ii) Αν το x
0
δεν είναι σηµείο συσσωρεύσεως του Α 1 τότε, η f εξ ορισµού, θεωρείται συνεχής
στο σηµείο αυτό.
iii) Μια συνάρτηση λέγεται συνεχής αν είναι συνεχής σε κάθε σηµείο του πεδίου ορισµού της.
5.3.2 Παρατηρήσεις
1. Αν το x
0
είναι σηµείο συσσωρεύσεως του Α τότε, µε βάση τον ορισµό του ορίου, θα
έχουµε:
«Για κάθε ε > 0 υπάρχει δ > 0 , τέτοιο ώστε | f( x) − f( x0
)| < ε για κάθε x∈ A µε
0 < | x− x | < δ ». (1)
0
Προφανώς το x
0
ικανοποιεί τη σχέση | f( x) − f( x0
)| < ε . Εποµένως, στην περίπτωση αυτή, η
φράση «για κάθε x∈ A µε 0 < | x− x0
| < δ » µπορεί να αντικατασταθεί από τη φράση «για
κάθε x∈ A µε | x− x0
| < δ ». (Ισοδύναµα, για κάθε x∈ A∩( x0
− δ , x0 + δ ) ). Ακόµη, αν το
x
0
είναι µεµονωµένο σηµείο του Α, τότε προφανώς ισχύει η παραπάνω συνθήκη (1).
Εποµένως η συνθήκη (1) είναι ικανή και αναγκαία για να είναι η f συνεχής στο x
0
.
2. Αν η f : B→ R είναι συνεχής στο σηµείο x
0
, το οποίο είναι σηµείο συσσωρεύσεως του
συνόλου Β, τότε, εφαρµόζοντας την πρόταση 5.2.17, για κάθε συνάρτηση g : A→ B µε την
ιδιότητα lim g ( u ) = x 0
, όπου a ∈R
∪{ −∞ , +∞}
, θα έχουµε:
u→a lim f ( g( u)) = lim f( x) = f( x ) = f(lim g( u))
.
0
u→a x→x0
u→a
5.3.3 Παραδείγµατα
1. Οι πολυωνυµικές συναρτήσεις είναι συνεχείς σε οποιοδήποτε σηµείο του πεδίου
m m−1 m m−1
lim amx + am−
1x + + a1x+ a0 = amx0 + am−
1x0
+ +
ax 1 0
+ a 0
.
ορισµού τους καθώς, ( )
x→x0
Γενικότερα, οι ρητές συναρτήσεις είναι συνεχείς (ο παρονοµαστής δεν µηδενίζεται στα
σηµεία του πεδίου ορισµού τους).
Έχουµε ήδη δείξει (πρόταση 5.1.11) ότι οι εκθετικές συναρτήσεις είναι συνεχείς.
Επίσης δείξαµε (πρόταση 5.1.16) ότι οι τριγωνοµετρικές συναρτήσεις είναι συνεχείς.
2. Η συνάρτηση f :
R→
R µε τύπο f ( x) = [ x]
δεν είναι συνεχής στα σηµεία x= k∈Z .
Πράγµατι, αν k ∈Z , τότε θεωρούµε τα διαστήµατα ( k − 1, k)
και ( k, k + 1) .
Αν x∈( k − 1, k)
τότε f ( x) = k − 1 και εποµένως lim f ( x) = k − 1 .
x→k
−
1 Στην περίπτωση αυτή το x
0
λέγεται µεµονωµένο σηµείο του Α.

42
Αν x∈ ( k, k + 1) τότε f ( x)
lim f ( x ) , η f δεν είναι συνεχής στο k.
x→k = k και εποµένως lim f ( x)
= k . Εφόσον δεν υπάρχει το
x→k
+
3. Θεωρούµε τη συνάρτηση f :( −∞,5]
→ R , η οποία ορίζεται ως εξής:
⎧ 4x
−1
⎪ αν x ≤1,
2
x + x+
1
⎪
f( x)
= ⎨2 − x αν 1 < x < 3,
⎪ 2
x − 5x+ 3 αν 3≤ x<
5,
⎪
⎪⎩ 2 αν x = 5
Να εξεταστεί σε ποια σηµεία του πεδίου ορισµού της είναι συνεχής.
Λύση: Στα διαστήµατα ( −∞ ,1), (1, 3) και (3, 5) είναι συνεχής γιατί διατηρεί τον ίδιο ρητό ή
πολυωνυµικό τύπο. Αποµένουν τα σηµεία 1, 3 και 5.
Σηµείο x=1: Σύµφωνα µε τον ορισµό 5.3.1, εξετάζουµε πρώτα αν υπάρχει το όριο lim f ( x)
.
x→1
4x
−1
Παίρνουµε τα πλευρικά όρια: Επειδή f( x)
= για x < 1, έχουµε lim f ( x)
=
2
−
x + x+
1
x→1
4x
−1
lim = 1 . Επειδή f ( x) = 2− x για 1< x < 3, έχουµε lim f ( x)
= lim(2 − x) = 1 . Άρα
x→1
2
+
x + x + 1
x→1
x→1
4−1
υπάρχει το lim f ( x)
και ισούται µε 1. Αλλά f (1) = = 1 , οπότε η f είναι συνεχής στο
x→1
2
1 + 1+
1
σηµείο x=1.
Σηµείο x=3: Επειδή f ( x) = 2− x για 1< x < 3, έχουµε
2
f( x) = x − 5x+ 3 για 3< x < 5, έχουµε
x→3
x→3
+
lim f ( x)
= lim(2 − x) =− 1. Επειδή
x→3
−
x→3
2
lim f ( x)
= lim( x − 5x+ 3) =− 3 . ∆εν υπάρχει
x→3
λοπόν το lim f ( x)
και συνεπώς, η f δεν είναι συνεχής στο σηµείο x=3.
y
3
2
1
-∞
O
1
3
5
x
-1
-3
Σηµείο x=5: Επειδή το 5 είναι δεξιό άκρο του διαστήµατος ( −∞ ,5], το
µε το
x→5
−
x→5
lim f ( x)
συµπίπτει
2
lim f ( x)
. Εποµένως, lim f ( x)
= lim( x − 5x+ 3) = 3 . Ακόµη, f (5) = 2 . Συνεπώς, η f
δεν είναι συνεχής στο σηµείο x=5.
x→5
x→5

43
4. Θεωρούµε τη συνάρτηση f :
R→
R µε τον ακόλουθο τύπο:
⎧ 2
2 − + 1−
x x ax
⎪
αν x < −1,
f( x) = ⎨ x + 1
⎪ 3
⎩x + bx + 2 αν −1≤
x
Να προσδιοριστούν τα ab∈ , R ώστε η παραπάνω συνάρτηση να είναι συνεχής.
Λύση: Η συνάρτηση f έχει πράγµατι πεδίο ορισµού το R γιατί η υπόρριζη ποσότητα
2
2x
− x + 1 είναι πάντα θετική (γιατί;).
Εφόσον η f είναι συνεχής στο -1, θα έχουµε
x→−1
−
lim f( x) = f( − 1) και εποµένως,
x→−1
−
[ f x x+ ] = f − ⋅ = . Αλλά lim [ f( x)( x 1) ]
lim ( )( 1) ( 1) 0 0
Εποµένως 2+ a= 0⇔ a=− 2.
Για a =− 2 ο τύπος της συνάρτησης γίνεται
Εποµένως,
lim f ( x)
= lim
x→−1
−
x→−1
−
+ = lim ( 2x )
2 x 1 ax
x→−1
− + − = 2 + a .
⎧ 2
2x − x+ 1+
2x
⎪
αν x 2
⎪⎩
x − 4
Να προσδιοριστεί το a ∈ R , ώστε η f να είναι συνεχής στο σηµείο 2.

44
3. Να προσδιορίσετε τα ab∈ , R , ώστε η συνάρτηση f µε τύπο
2 2
⎧ ax + bx− 12, αν x<
1
⎪
f( x) = ⎨5, αν x = 1
⎪
⎩ax + b, αν x > 1
να είναι συνεχής.
Εκµεταλλευόµενοι τις ιδιότητες των ορίων (θεώρηµα 5.1.6) µπορούµε εύκολα να
αποδείξουµε την επόµενη πρόταση:
5.3.4 Πρόταση
Υποθέτουµε ότι οι συναρτήσεις f και g είναι συνεχείς στο σηµείο x
0
του κοινού πεδίου ορισµού
τους Α. Τότε και οι παρακάτω συναρτήσεις είναι συνεχείς στο σηµείο x
0
:
i) λ f , όπου λ ∈R , ii) | f | , iii) f ± g , iv) fg, v) f g , αν gx≠ ( ) 0 για κάθε x ∈ A ,
vi) k f , αν f( x) ≥ 0 για κάθε x∈ A , όπου k θετικός ακέραιος. ■
Αν χρησιµοποιήσουµε την πρόταση 5.1.14, µπορούµε εξίσου εύκολα να αποδείξουµε την
ακόλουθη πρόταση:
5.3.5 Πρόταση
Θεωρούµε τις συναρτήσεις f : A→B⊆R και g:
B→ R . Υποθέτουµε ότι η f είναι συνεχής σ’
ένα σηµείο x0
∈ A και ότι η g είναι συνεχής στο σηµείο f ( x0
) ∈ B.
Τότε η g f είναι συνεχής στο x
0
.
■
Συνδυάζοντας κανείς τις δύο προηγούµενες προτάσεις µε το παράδειγµα 5.3.3.1, µπορεί να
κατασκευάσει συναρτήσεις µε ένα σωρό πολύπλοκους τύπους. (Αρκεί να περιοριστεί στα
πεδία ορισµού για τα οποία έχουν νόηµα οι τύποι αυτοί).
2 3x
− x x − e
Έτσι, η συνάρτηση µε τύπο f( x) = cos(2 + x+ 1) −
3
x + sin(2 x)
είναι συνεχής.
Γνωρίζουµε όµως (βλ. Παράδειγµα 5.3.3.2)) ότι, µε την ίδια περίπου ευκολία, µπορεί να
κατασκευάσει κανείς συναρτήσεις που δεν είναι συνεχείς. Ίσως ένα από τα πιο παθολογικά
παραδείγµατα είναι η συνάρτηση Dirichlet, η οποία ορίζεται ως εξής:
⎧1 αν o x είναι ρητός,
f( x)
= ⎨
⎩ 0 αν ο x είναι άρρητος

45
Χρησιµοποιώντας τον ορισµό του πεπερασµένου ορίου µπορεί να δείξει κανείς ότι δεν
υπάρχει το όριο lim f ( x)
για κάθε x0
∈R . Άρα η f δεν είναι πουθενά συνεχής!
x→x0
Στη συνέχεια θα ασχοληθούµε µε ορισµένα θεµελιώδη θεωρήµατα που αφορούν τις συνεχείς
συναρτήσεις. Ξεκινάµε µε ένα επώνυµο θεώρηµα:
5.3.6 Θεώρηµα του Bolzano
Θεωρούµε µια συνεχή συνάρτηση f :[ a, b]
→ R , ορισµένη στο κλειστό διάστηµα [ ab. , ]
Υποθέτουµε ότι η f παίρνει ετερόσηµες τιµές στα άκρα του διαστήµατος [ ab, , ] δηλαδή
f( a) f( b ) < 0.
Τότε η f έχει µια τουλάχιστον ρίζα στο ανοικτό διάστηµα ( a, b ).
■
Η απόδειξη του θεωρήµατος αυτού είναι αρκετά λεπτή, γι’ αυτό και την παραθέτουµε σε
ειδικό παράρτηµα στο τέλος αυτού του κεφαλαίου.
Η γεωµετρική σηµασία του θεωρήµατος του Bolzano είναι η ακόλουθη: Αν φανταστούµε µια
συνεχή γραµµή, η οποία συνδέει δύο σηµεία του καρτεσιανού επιπέδου R×
R που
βρίσκονται εκατέρωθεν του άξονα των x τότε, η γραµµή αυτή θα τέµνει τον άξονα των x.
y
f(a)
ρίζα
O
a
ξ
b
x
f(b)
5.3.7 Παρατήρηση
Αν η σχέση f( a) f( b ) < 0 αντικατασταθεί από τη σχέση f( a) f( b) ≤ 0, τότε η διατύπωση
του θεωρήµατος Bolzano τροποποιείται ως εξής: «Θεωρούµε µια συνεχή συνάρτηση
f :[ a, b]
→ R , ορισµένη στο κλειστό διάστηµα [ ab. , ] Υποθέτουµε ότι f( a) f( b) ≤ 0. Τότε η f
έχει µια τουλάχιστον ρίζα στο κλειστό διάστηµα [ a, b ]».

46
5.3.8 Πόρισµα
Από το θεώρηµα του Bolzano προκύπτει ότι αν µια συνεχής συνάρτηση, ορισµένη σ’ ένα
διάστηµα (πεπερασµένο ή άπειρο) δεν έχει ρίζες, τότε διατηρεί σταθερό πρόσηµο. ■
5.3.9 Παραδείγµατα
1. ∆ίνεται η συνάρτηση f : R→
R µε
4 3 2
f ( x) = x − x + x − 5x+ 1. Να δειχθεί ότι η f έχει µια
τουλάχιστον ρίζα στο διάστηµα ( − 1,1) .
Λύση: Παρατηρούµε ότι
4 3 2
f ( − 1) = ( −1) −( − 1) + ( −1) −5( − 1) + 1= 9> 0 και
4 3 2
f (1) = 1 − 1 + 1 −5 ⋅ 1 + 1 =− 3 < 0 . Η f παίρνει λοιπόν ετερόσηµες τιµές στα άκρα του
διαστήµατος. Σύµφωνα µε το θεώρηµα Bolzano, υπάρχει ξ ∈( − 1,1) µε f ( ξ ) = 0.
⎛ π ⎞
2. Να δειχθεί ότι η εξίσωση cos x + 1 = x έχει µια τουλάχιστον ρίζα στο διάστηµα ⎜0, ⎟
⎝ 2 ⎠ .
Λύση: Θεωρούµε τη συνεχή συνάρτηση f :
⎛π
⎞ π
ότι f (0) = 2 > 0 και f ⎜ ⎟ = 1 − < 0
⎝ 2⎠
2
συµπέρασµα.
R→
R µε f ( x) = cosx+ 1− x. Παρατηρούµε
(γιατί π > 2 ). Από το θεώρηµα Bolzano προκύπτει το
5.3.10 Πρόταση (ύπαρξη n-στής ρίζας µη αρνητικού αριθµού)
Έστω a ≥ 0 και n θετικός ακέραιος. Τότε υπάρχει (ακριβώς ένας) µη αρνητικός αριθµός ξ µε
n
την ιδιότητα ξ = a .
Απόδειξη: Μπορούµε να υποθέσουµε ότι a > 0. Θεωρούµε τη συνάρτηση f : R→
R µε
n
f ( x)
= x − a, για κάθε x∈R .
n
Έχουµε f(0) =− a< 0 . Επειδή lim f( x) = lim ( x − a)
=+∞, υπάρχει δ > 0 µε την ιδιότητα
x→+∞
x→+∞
f( x ) > 1> 0, για κάθε x ≥ δ . Ο περιορισµός της f στο διάστηµα [0, δ ] παίρνει ετερόσηµες
τιµές στα άκρα του διαστήµατος αυτού. Σύµφωνα µε το θεώρηµα Bolzano, η f έχει µια ρίζα
n
στο διάστηµα αυτό, δηλαδή, υπάρχει ξ ∈ [0, δ ] µε ξ = a . ■
Από το θεώρηµα Bolzano προκύπτει ένα ενδιαφέρον πόρισµα:

47
5.3.11 Πόρισµα (θεώρηµα ενδιάµεσης τιµής)
Θεωρούµε µια συνεχή συνάρτηση f :[ a, b]
→ R , ορισµένη στο κλειστό διάστηµα [ ab. , ] Αν λ
είναι ένας αριθµός που βρίσκεται µεταξύ των f ( a ) και f ( b ), τότε υπάρχει ξ ∈ [ ab , ] τέτοιο
ώστε, f ( ξ )
= λ .
Απόδειξη: Η περίπτωση λ = f ( a) = f( b)
είναι τετριµένη. Υποθέτουµε f ( a) < λ < f( b)
. Η
συνάρτηση g:[ a, b]
→ R µε τύπο gx ( ) = f( x)
− λ παίρνει στα άκρα του διαστήµατος [ ab , ]
ετερόσηµες τιµές. Από το θεώρηµα του Bolzano προκύπτει ότι υπάρχει ξ ∈ ( ab , ) τέτοιο
ώστε, g( ξ ) = 0 ⇔ f( ξ)
= λ. Η περίπτωση f ( a) > λ > f( b)
αντιµετωπίζεται παρόµοια. ■
5.3.12 Παρατήρηση
Η γεωµετρική ερµηνεία του θεωρήµατος είναι η ακόλουθη: Κάθε οριζόντια ευθεία που κείται
µεταξύ των ευθειών y = f( a)
και y = f( b)
τέµνει τη γραφική παράσταση της f σ’ ένα
y
y=f(a)
y=λ
y=f(b)
O
a ξ 1
ξ 2
ξ 3
b
x
τουλάχιστον σηµείο.
5.3.13 Παρατήρηση
Από το προηγούµενο πόρισµα προκύπτει ότι η εικόνα ενός διαστήµατος Α (πεπερασµένου ή
άπειρου), µέσω µιας συνεχούς συνάρτησης, είναι επίσης διάστηµα. Πράγµατι, αν y
1
, y
2
είναι οι εικόνες δύο σηµείων x
1
και x
2
, µε x1 < x2, τότε και κάθε τιµή y µεταξύ των y
1
και
y
2
είναι εικόνα κάποιου σηµείου x του διαστήµατος
1 2
[ x , x ], (το διάστηµα [ x1, x
2]
περιέχεται στο πεδίο ορισµού Α της συνάρτησης, εφόσον το Α είναι διάστηµα).
Άλυτες ασκήσεις
1. Να δείξετε ότι οι ακόλουθες εξισώσεις έχουν µια τουλάχιστον ρίζα στο διάστηµα (0,1) :

48
(i)
4
5
x + 30x− 29 = 0 και (ii) 5x
+ 25x− 11= 0.
2. ∆είξτε ότι η εξίσωση x+ cos x = 4 έχει µια τουλάχιστον ρίζα στο διάστηµα (0, 2 π ) .
3. ∆ίνονται οι συνεχείς συναρτήσεις f και g, για τις οποίες ισχύει f( x) − g( x)
= cx , όπου c ∈ R . Αν η
εξίσωση f( x ) = 0 έχει δύο ρίζες ετερόσηµες r
1
< 0 και r
2
> 0 , τότε η εξίσωση gx= ( ) 0 έχει µια
τουλάχιστον ρίζα στο διάστηµα [ r1, r
2]
.
4. ∆ίνονται οι συνεχείς συναρτήσεις f, g:[ a, b]
→ R , για τις οποίες ισχύει f( a) g( b ) > 0. ∆είξτε ότι η
εξίσωση
f( x) g( x)
0
x−a + x−b
=
έχει µια τουλάχιστον ρίζα στο διάστηµα ( ab , ).
Εξίσου σηµαντικό για την κατανόηση της συµπεριφοράς των συνεχών συναρτήσεων που
ορίζονται σε κλειστά διαστήµατα είναι το επόµενο θεώρηµα.
5.3.14 Θεώρηµα µέγιστης-ελάχιστης τιµής
Θεωρούµε µια συνεχή συνάρτηση f :[ a, b]
→ R .
y
M
Τότε η f είναι φραγµένη.
Επιπλέον, αν M = sup{ f( x) | x∈ [ a, b]}
και
m= inf{ f( x) | x∈ [ a, b]}
, τότε υπάρχουν x1,
x
2
m
∈ [ ab , ] µε f ( x 1
) = M και f ( x 2
) = m . ■
O
a
x 1
x 2
b
x
Και αυτού του θεωρήµατος η απόδειξη είναι αρκετά λεπτή και παρατίθεται στο παράρτηµα.
Στη συνέχεια θα ασχοληθούµε µε την ύπαρξη αντιστρόφου µιας συνεχούς συνάρτησης. Η
επόµενη πρόταση αναφέρεται στη µονοτονία των συνεχών συναρτήσεων.
5.3.15 Πρόταση
i) Θεωρούµε µια συνεχή συνάρτηση f :[ a, b]
→ R . Αν η f είναι 1-1 τότε είναι γνησίως
µονότονη.
ii) Γενικότερα, αν f :
A→ R είναι µια συνεχής και 1-1 συνάρτηση, όπου Α είναι διάστηµα
(πεπερασµένο ή άπειρο, κλειστό ή όχι), τότε η f είναι γνησίως µονότονη.
*Απόδειξη: i) Υποθέτουµε ότι f ( a) < f( b)
. Αρχικά θα αποδείξουµε ότι αν a< s< b, τότε
f ( a) < f( s) < f( b)
.
Επειδή η f είναι 1-1, f ( s) ≠ f( a)
. Έστω ότι f () s < f()
a .
Ο περιορισµός της f στο διάστηµα [, s b ] είναι (προφανώς) συνεχής.

49
Επειδή f () s < f() a < f()
b , από το θεώρηµα
ενδιάµεσης τιµής προκύπτει ότι υπάρχει t∈
(, s b)
y
µε f () t = f( a)
. Αυτό είναι άτοπο, γιατί η f είναι
f(b)
1-1 ( t ≠ a). Άρα f () s > f()
a .
Με παρόµοιο συλλογισµό δείχνουµε ότι
f () s < f()
b .
Έστω τώρα a≤ x1 < x2
≤ b. Από το προηγούµενο
συµπέρασµα προκύπτει ότι f ( a) ≤ f( x1
) < f( b)
.
f(a)
f(s)
O a s t b
x
Εφαρµόζοντας πάλι το προηγούµενο συµπέρασµα στον περιορισµό της f στο διάστηµα
[ x1
, b ], προκύπτει ότι f ( a) ≤ f( x1) < f( x2) ≤ f( b)
. Εποµένως η f είναι γνησίως αύξουσα.
Αν τώρα f ( a) > f( b)
, τότε − f ( a) f( x2)
αντιµετωπίζεται παρόµοια. ■
Σύµφωνα µε την παρατήρηση 5.3.13, αν f :
A→ R είναι µια συνεχής και 1-1 συνάρτηση,
όπου Α διάστηµα, τότε το B = f( A)
είναι διάστηµα και ορίζεται η αντίστροφη
−
f 1 : B→
A
συνάρτηση. Με βάση την πρόταση 5.3.15, η f, άρα και η
1
f − , είναι γνησίως µονότονες, του
ίδιου τύπου µονοτονίας. ∆εν γνωρίζουµε αν η
1
f − είναι συνεχής. Η επόµενη πρόταση 5.3.17
µας το εξασφαλίζει. Ας δούµε πρώτα ένα λήµµα.
5.3.16 Λήµµα*
Έστω f :[ ab , ] → [ f( a), f( b)]
µια συνεχής και γνησίως αύξουσα συνάρτηση, όπου a< b και
− 1 −1
−1
f :[ f( a), f( b)] → [ a, b]
η αντίστροφή της. Τότε lim f ( y)
= a και lim f ( y)
= b.
y→
f ( a)
+
y→
f ( b)
−

50
Απόδειξη: Έστω ε > 0 . Μπορούµε να υποθέσουµε ότι ε < b− a, οπότε [ aa , + ε ) ⊆ [ ab , ].
Έστω δ = f( a+ ε ) − f( a) > 0. Τότε f ([ a, a+ ε )) = [ f( a), f( a+ ε )) = [ f( a),
f( a) + δ ).
Εποµένως,
−
f
1 ([ f( a),
f( a) + δ )) = [ a, a+ ε ). Αν λοιπόν 0 < y− f( a)
< δ , τότε
−1
0 ( )
< f y − a< ε . Η δεύτερη περίπτωση εξετάζεται παρόµοια. ■
5.3.17 Πρόταση
Έστω f : A→ B= f( A)
µια συνεχής και 1-1 συνάρτηση, όπου Α διάστηµα, που δεν είναι
µονοσύνολο. Τότε και η αντίστροφή της
−
f 1 : B A
→ είναι συνεχής.
*Απόδειξη: Υποθέτουµε ότι η f είναι γνησίως αύξουσα. Έστω y0 = f( x0)
∈ B, όπου x0
∈ A .
Αν το x
0
είναι αριστερό άκρο του διαστήµατος Α, τότε το y0 = f( x0)
είναι αριστερό άκρο
του διαστήµατος Β. Στην περίπτωση αυτή υπάρχει b> x0
µε [ x0
, b]
⊆ A. Εφαρµόζοντας το
προηγούµενο λήµµα για τον περιορισµό της f στο διάστηµα [ x0
, b ], συµπεραίνουµε ότι
−1
lim f ( y)
= x .
y→
y
+
0
0
Αν το x
0
είναι δεξιό άκρο του διαστήµατος Α, τότε το y0 = f( x0)
είναι δεξιό άκρο του
διαστήµατος Β. Στην περίπτωση αυτή υπάρχει a< x0
µε [ a, x0
] ⊆ A. Εφαρµόζοντας το
προηγούµενο λήµµα για τον περιορισµό της f στο διάστηµα [ a, x
0]
, συµπεραίνουµε ότι
−1
lim f ( y)
= x .
y→
y
−
0
0
Αν τέλος, το x
0
είναι εσωτερικό σηµείο του διαστήµατος Α, τότε υπάρχουν a< x0
< b µε
[ ab , ] ⊆ A. Εφαρµόζοντας το προηγούµενο λήµµα για τον περιορισµό της f στα διαστήµατα
−1 −1
[ a, x
0]
και [ x0
, b ], συµπεραίνουµε ότι lim f ( y) = lim f ( y)
= x .
y→y −
0 y→y
+
0
Αν η f είναι γνησίως φθίνουσα, τότε η − f : A→− B= { −y| y∈ B}
είναι συνεχής και γνησίως
0
αύξουσα. Παρατηρούµε ότι
= − , όπου φ :B →− B είναι η συνεχής συνάρτηση
−1 −1
f ( f)
φ
µε τύπο φ ( y)
=− y. Η
1
f −
σαν σύνθεση συνεχών συναρτήσεων είναι συνεχής. ■
5.4 Εκθετικές και λογαριθµικές συναρτήσεις-κυκλοµετρικές συναρτήσεις
Εκθετικές και λογαριθµικές συναρτήσεις
Έστω a > 0 . Θεωρούµε τη συνάρτηση exp
a
: R → (0, +∞)
µε τύπο exp ( x x
a
) = a . Έχουµε
δείξει (πρόταση 5.1.11) ότι η συνάρτηση αυτή είναι συνεχής. Ακόµη, αν a > 1, η exp a
είναι
γνησίως αύξουσα, αν a = 1 είναι σταθερή ενώ αν a < 1, τότε είναι γνησίως φθίνουσα.

51
y
f(x)=2 x
g(x)=(1/2) x
1
O
x
5.4.1 Πρόταση
i) Αν a > 1, τότε lim
x→+∞
a
x
x
=+∞ και lim a = 0 .
x→−∞
x
ii) Αν a < 1 , τότε lim a = 0 και lim a
x = +∞ .
x→+∞
Απόδειξη: i) Έστω 0
x→−∞
n
ε > . Η ακολουθία ( )
Άρα, υπάρχει θετικός ακέραιος n
0
µε
n
a
a απειρίζεται θετικά (παράδειγµα 2.10.6.4(i)).
> ε , για κάθε n≥
n0
. Εφόσον η exp a
είναι γνησίως
x n0
αύξουσα, θα έχουµε a ≥ a > ε , για κάθε x∈ [ n0
, +∞ ).
x 1 1
Επίσης, lim a = lim = lim . Επειδή lim a
u = +∞ , από το (viii) της πρότασης
x→−∞ x→−∞ − x
u
u
a →+∞ a
u→+∞
1
5.2.14, προκύπτει ότι lim = 0 .
u→+∞
u
a
x
−1 −
1
lim lim x
−
u
x
−
a a lim a 0 lim lim 1 − x
−
lim
1 u
a = a = a = +∞ . ■
−
−
ii) = ( ) = ( ) = και ( ) ( )
1
1
x→+∞ x→+∞ u→−∞ a > 1
x→−∞ x→−∞ u→+∞ a > 1
Αν a > 0 και a ≠ 1, τότε µε βάση την παρατήρηση 5.3.13, η συνάρτηση exp a
είναι επί του
(0, +∞ ) . Εποµένως (όντας και 1-1) αντιστρέφεται.
5.4.2 Ορισµός
Έστω a > 0 και a ≠ 1. Θέτουµε
αριθµός
y= log a
x µε την ιδιότητα
= +∞ →R . Αν x > 0 , τότε ο µοναδικός
−1
loga
exp
a
: (0, )
y
a
= x λέγεται λογάριθµος µε βάση το a του x.
∆ηλαδή, ισχύει η ισοδυναµία
y
y = log x⇔ a = x.
a
5.4.3 Παρατήρηση
Από την πρόταση 5.3.17 συµπεραίνουµε ότι η συνάρτηση log
a
: (0, + ∞)
→R είναι συνεχής.

52
5.4.4 Ορισµός
Αν a= e= 2,71828182845904.... τότε θέτουµε ln x = log e
x , για κάθε x > 0 . Ο αριθµός ln x
λέγεται νεπέριος ή φυσικός λογάριθµος του x.
y
y = e x
1
O
1
y = lnx
x
Στο παραπάνω σχήµα παριστάνονται οι γραφικές παραστάσεις των συναρτήσεων
y
x
= e και
της αντίστροφής της
y = ln x.
Οι δύο γραφικές παραστάσεις είναι συµµετρικές ως προς την ευθεία y
= x.
5.4.5 Πρόταση
Έστω a > 0 και a ≠ 1. Τότε ισχύουν τα εξής:
i) log
a
(1) = 0 .
ii) log − 1 x =− log
a a
x .
iii) log ( xy) = log x+ log y, για κάθε xy∈ , (0, +∞ ).
a a a
iv) log ⎛ x
⎜
⎞ ⎟ = log x − log
⎝ y ⎠
a a a
y
, για κάθε xy∈ , (0, +∞ ).
λ
v) log
a( x ) = λ loga
x , για κάθε x∈ (0, +∞ ) και λ ∈R .
loga
x
vi) Αν b > 0 και b ≠ 1 , τότε logb
x = (τύπος αλλαγής βάσης).
log b
Απόδειξη: i) Επειδή
0
a = 1 , έπεται log (1) 0
a
a
= .
−1
−loga x loga
x
ii) ( a ) = a = x. Εποµένως, log − 1 x = − log
a a
x .
iii)
log a x+
log a y log a x log a y
a a a xy
= = . Εποµένως log x + log y = log ( xy)
.
a a a

53
iv)
loga
x
loga x−loga y loga x −loga
y a x
a = a a = = . Εποµένως log ⎛ x
log log
loga
y
⎜
⎞ ⎟ = x −
a y
⎝ y ⎠
λ
λ
a = a = x . Εποµένως log ( x ) = λ log x .
λ loga
x loga
x
v) ( )
⋅
vi) ( ) log
λ
a
a
a a a
log log log b
ab b x
x
ab logb
x
a = a = b = x. Εποµένως, logab⋅ logb x= loga x⇔ logb
x= log a
x
loga
b . ■
y .
5.4.6 Πρόταση
i) Αν a > 1, τότε lim log a
x→+∞
x→+∞
x =+∞ και lim log x = −∞ .
a
+
x→0
ii) Αν a < 1 , τότε lim log a
x =−∞ και lim log x = +∞ .
a
+
x→0
Απόδειξη: i) Έστω ε > 0. Θέτουµε δ = a ε > 0. Εφόσον η log a
είναι γνησίως αύξουσα, για
κάθε x > δ θα έχουµε loga
x > log
aδ = ε .
Εποµένως, lim log a
x =+∞.
x→+∞
−
Για ε > 0, θέτουµε δ = a ε > 0. Αν 0< x < δ , τότε log x < log δ =− ε .
ii) lim log x =− lim log ( )
−1
x = − +∞ =−∞ και
a
x→+∞ x→+∞ a −
a
1 > 1
lim log x =− lim log x = −( −∞ ) =+∞. ■
a
−1
x→−∞ x→−∞ a −
a
1 > 1
a
a
5.4.7 Παραδείγµατα
2
x
4−5x
⎛2⎞ ⎛3⎞
1. Να λυθεί η ανίσωση ⎜ ⎟ < ⎜ ⎟ .
⎝3⎠ ⎝2⎠
2 2
x 4−5x x 5x−4
⎛2⎞ ⎛3⎞ ⎛2⎞ ⎛2⎞
2
Λύση: ⎜ ⎟ < ⎜ ⎟ ⇔ ⎜ ⎟ < ⎜ ⎟ ⇔ exp
2/3( x ) < exp
2/3(5x−4)
.
⎝3⎠ ⎝2⎠ ⎝3⎠ ⎝3⎠
2
Επειδή 1
3 < , η συνάρτηση exp
2/3
είναι γνησίως φθίνουσα και εποµένως πρέπει
2 2
x x x x
> 5 −4⇔ − 5 + 4> 0⇔ ( x−1)( x− 4) > 0 ⇔ ( x< 1 ή x> 4) .
2. Να λυθεί η εξίσωση
2
x x 2
a − − = 1, όπου 0
a > .
Λύση: Έστω a = 1. Τότε η σχέση
2
x x 2
a − − = 1 ισχύει για κάθε x∈R .
Έστω a ≠ 1. Τότε η σχέση
x=− 1 ή x= 2.
a
2
x −x−2 0
= 1 = a είναι ισοδύναµη µε τη σχέση
x
2
−x− 2= 0⇔
x
3. Να δειχθεί ότι οι συναρτήσεις f, g :(0, + ∞)
→R µε τύπους f ( x)
= x και
g( x)
= x
sin x
είναι συνεχείς.
Απόδειξη: Έχουµε
x
x ln( x ) xln
x
f ( x)
= x = e = e , δηλαδή η f είναι η σύνθεση των συνεχών
συναρτήσεων
y
x
= e και ln
y = x x. Άρα η f είναι συνεχής.

54
Οµοίως,
gx ( ) x e
sin x sin xln
x
= = και η g είναι σύνθεση των συνεχών συναρτήσεων
y
x
= e και
y = sin xln
x. Εποµένως και αυτή είναι συνεχής.
4. Να αποδείξετε τα ακόλουθα:
(i) Αν abc> , , 0, b ≠ 1 και ab ≠ 1, τότε
log
ab
logb
c
c = .
1 + log a
(ii) log23 ⋅ log34 ⋅ log45 log ( n+ n
1) = log
2( n+
1) .
1 1
(iii) + > 2 , όπου π = 3,1415926535897932384626433832795...
log π log π
2 5
Απόδειξη: (i) Από τον τύπο αλλαγής βάσης (πρόταση 5.4.3 (vi)) έχουµε:
logbc
logbc
= =
log a+ log b log a+ 1
.
b b b
log 4
⋅
log 3
(ii) log23 ⋅ log34 ⋅ log45 log ( n + n
1) =
2
log23
⋅
2
b
log2
5
log2
4
log2
n
log
2( n −1)
log
ab
logb
c
c =
log ( ab)
2
b
log
2
( n + 1)
=
log n
= log
2( n + 1) .
1 1 log2
2 log5
5
(iii) + = + = logπ 2 + logπ 5 = log
π(2 ⋅ 5) = logπ 10 . Εποµένως,
log2π log5π log2π log5π
1 1
logπ
10 2 2
+ > 2⇔ logπ 10> 2⇔ π > π ⇔ 10> π ⇔
log π log π
2 5
π < 10 . Η τελευταία σχέση ισχύει γιατί, 10 = 3,16227.... > π.
5.4.8 Πρόταση
1
Ισχύει: 1− ≤lnx
≤ x − 1, για κάθε x > 0 .
x
x
Απόδειξη: Αν στη σχέση e ≥ 1+ x θέσουµε x − 1 αντί x, παίρνουµε
τους φυσικούς λογαρίθµους και στα δύο µέλη, έχουµε ln x ≤ x − 1.
Αν στην τελευταία σχέση θέσουµε
1
ln x ≥1−
. ■
x
1
x −
αντί x, θα πάρουµε
x
e
− 1
≥ x. Παίρνοντας
−1 1 1
ln( x ) ≤ −1 ⇔ −ln x≤ −1
⇔
x
x
5.4.9 Παραδείγµατα
1 1 1 1
1. Να βρεθεί το όριο της ακολουθίας a n
= + + + + , n = 1, 2, …
n n+ 1 n+
2 2n
1
Λύση: Στη σχέση 1− ≤lnx
≤ x − 1, µε x > 0 , που αποδείξαµε προηγουµένως, θέτουµε
x
k + 1
x = , όπου k = n, n+ 1, …,2n.
k

55
k ⎛k + 1⎞
k + 1 1 1
Παίρνουµε 1− ≤ln⎜
⎟≤ −1⇔ ≤ ln( k + 1) −lnk
≤ .
k + 1 ⎝ k ⎠ k k + 1
k
1 1
Αθροίζοντας τις σχέσεις ≤ ln( k + 1) −ln
k ≤ , k = n, n+ 1, …,2n
κατά µέλη, παίρνουµε
k + 1
k
1 1 1
+ + + ≤ (ln( n + 1) − ln n) + ( ln( n+ 2) − ln( n + 1) ) + (ln( n + 3) − ln( n + 2) )
n+ 1 n+ 2 2n+
1
1 1 1
+ + (ln(2n+ 1) − ln(2 n)
) ≤ + + + ⇔
n n+
1 2n
1 1 1 1 1 1 1 1
⇔ + + + + − ≤ ln(2n+ 1) −ln
n≤ + + + ⇔
n n+ 1 2n 2n+ 1 n n n+
1 2n
1 1 ⎛2n
+ 1⎞
⇔ an
+ − ≤ln
⎜ ⎟≤an
2n+ 1 n ⎝ n ⎠
1 1 ⎛2n
+ 1⎞
Από τη σχέση an
+ − ≤ln
⎜ ⎟
2n+ 1 n ⎝ n ⎠ παίρνουµε ⎛2n
+ 1⎞
1 1
an
≤ ln ⎜ ⎟− + .
⎝ n ⎠ 2n+
1 n
⎛2n
1 2 1 1 1
Άρα, ln
+ ⎞ ⎛ n
an
ln
+ ⎞
⎜ ⎟≤ ≤ ⎜ ⎟− + .
⎝ n ⎠ ⎝ n ⎠ 2n+
1 n
2n
+ 1
Είναι lim = 2 και limln x = ln 2 (εφόσον η συνάρτηση του λογαρίθµου είναι
n→+∞
n
x→2
⎛2n
+ 1⎞ συνεχής). Από την παρατήρηση 5.3.2.2 προκύπτει ότι lim ln ⎜ ⎟ = ln 2 .
n→+∞
⎝ n ⎠
1 1
⎡ ⎛2n+ 1⎞ 1 1⎤
⎛2n+
1⎞
Ακόµη, lim = lim = 0 . Άρα lim ln lim ln ln 2
n→+∞
2n+
1 n→+∞
n
n→+∞
⎢ ⎜ ⎟− + = =
n 2n 1 n
⎥ ⎜ ⎟ .
+
n→+∞
⎣ ⎝ ⎠ ⎦ ⎝ n ⎠
Από το κριτήριο παρεµβολής παίρνουµε lim a = ln 2 .
n→+∞
n
1 1 1
2. Να δειχθεί ότι η ακολουθία an
= 1+ + + + −lnn, n = 1,2, … συγκλίνει.
2 3 n
k + 1
1
Απόδειξη: Θέτουµε x = , k = 1,2, …,
n, στη σχέση 1− ≤lnx
≤ x − 1 και παίρνουµε
k
x
1 1
≤ ln( k + 1) −ln
k ≤ . Αθροίζοντας για k = 1, 2, …, n−1
παίρνουµε
k + 1
k
n−1 n−1
n n n
1 1 1 1 1 1 1
∑ ≤ln n≤∑ ⇔ ∑ −1≤ln n≤∑ − ⇔ ≤∑ −ln n≤1, δηλαδή έχουµε
k= 1 k + 1
k= 1k k= 1 k k= 1k n n k=
1 k
1
≤a n
≤ 1. Εποµένως η ακολουθία ( a
n
) είναι φραγµένη. Θα δείξουµε ότι είναι και γνησίως
n
1 1 ⎛n
+ 1⎞
φθίνουσα. Έχουµε, an+
1
− an
= − ln( n+ 1) + ln n= −ln
⎜ ⎟
n+ 1 n+ 1 ⎝ n ⎠ .
n+ 1 n+
1
1 ⎛n+ 1⎞ ⎛n+ 1⎞ ⎛n+ 1⎞ ⎛n+
1⎞
Αλλά < ln ⎜ ⎟ ⇔ 1 < ( n+ 1)ln ⎜ ⎟ ⇔ 1< ln ⎜ ⎟ ⇔ e<
⎜ ⎟ . Η
n+ 1 ⎝ n ⎠ ⎝ n ⎠ ⎝ n ⎠ ⎝ n ⎠
1
1 n +
⎛n
+ ⎞
τελευταία σχέση ισχύει, γιατί η ακολουθία ⎜ ⎟ , n = 1,2, … είναι γνησίως φθίνουσα και
⎝ n ⎠
έχει όριο τον e (παράδειγµα 2.9.2.1).
Εποµένως η ( a
n
) είναι γνησίως φθίνουσα και, όντας φραγµένη, συγκλίνει.

56
Σηµείωση: Το
⎛ 1 1 1 ⎞
lim ⎜1+ + + + −ln
n⎟
n→+∞⎝
2 3
n ⎠
συµβολίζεται µε το γράµµα γ και λέγεται
σταθερά του Euler.
3. Να δειχθεί ότι οι σειρές
Απόδειξη: Από τη σχέση
∞
n
∑ ln n και
n=
2
∞
1
∑ απειρίζονται θετικά.
ln n
n=
2
1
1− ≤lnn≤n− 1 προκύπτει ότι
n
n
1 n
1− ≤ lnn
και
n
1 1
≥ ,
ln n n − 1
για κάθε n = 2,3, …
Αλλά,
1
lim n 1−
= 1 (γιατί
n→+∞
n
n
1 n
1− < 1= 1 και
n
n
ακολουθία ( ln n ) δεν είναι µηδενική. Άρα
Επειδή
∞
∑
n=
2
∞
n=
2
n
1 1 1
1 − n 1
n
n
≥ 2 = 2
→ ) και εποµένως η
n
∑ ln n = +∞ .
∞
1
1
= ζ (1) =+∞, και η σειρά ∑ απειρίζεται θετικά.
n −1
ln n
n=
2
4. Να δειχθεί ότι
⎛ 1 ⎞
lim ⎜1+ ⎟ = e .
x→±∞⎝
x ⎠
x
Απόδειξη: Αρχικά εξετάζουµε την περίπτωση x →+∞. Έχουµε
1
x
⎛ x+ ⎞ ⎛ x+
1⎞
ln⎜ ⎟ x ln⎜ ⎟
⎝ x ⎠ ⎝ x ⎠
x
⎛ 1⎞ ⎛ x + 1⎞
⎜1+ ⎟ = ⎜ ⎟ =
⎝ x⎠ ⎝ x ⎠
= e = e . Λόγω της συνέχειας της εκθετικής συνάρτησης, αρκεί να αποδείξουµε
⎛ ⎛ x + 1⎞ ⎞
ότι lim ⎜xln ⎜ ⎟⎟
= 1.
x→+∞⎝
⎝ x ⎠⎠
x + 1
Θέτουµε αντί x, στη σχέση
x
1
1− ≤lnx
≤ x − 1 και παίρνουµε
x
1 ⎛ x + 1⎞
1
≤ln
⎜ ⎟≤
.
x + 1 ⎝ x ⎠ x
Πολλαπλασιάζοντας µε x (το x λαµβάνεται θετικό, γιατί τείνει στο +∞ ) παίρνουµε
x ⎛ x+
1⎞
≤ xln ⎜ ⎟≤1.
x+ 1 ⎝ x ⎠
x
Επειδή lim = 1, από το κριτήριο παρεµβολής προκύπτει ότι
x→+∞
x + 1
x x − x
⎛ ⎛ x + 1⎞ ⎞
lim ⎜xln ⎜ ⎟⎟
= 1.
x→+∞⎝
⎝ x ⎠⎠
⎛ 1⎞ ⎛ x+
1⎞ ⎛ x ⎞
Τώρα, αν x →−∞, έχουµε: lim ⎜1+ ⎟ = lim ⎜ ⎟ = lim ⎜ ⎟ =
x→−∞ x x→−∞ x x→−∞
⎝ ⎠ ⎝ ⎠ ⎝ x+
1⎠
⎛⎛ 1 ⎞ x ⎞ ⎛ 1 ⎞ x ⎛ 1 ⎞
= lim 1+ = lim 1+ lim = lim 1+
x→−∞⎜
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
( x 1) x 1 x→−∞ ( x 1) x→−∞ x 1 x→−∞
⎝ − + ⎠ + ⎟ ⎝ − + ⎠ + ⎝ − ( x+
1)
⎝
⎠
⎠
− ( x+ 1) − ( x+ 1) − ( x+
1)
Θέτουµε u =−x−1→+∞ και εφαρµόζουµε την πρόταση 5.2.17.
Είναι
− ( x+
1)
⎛ 1 ⎞ ⎛ 1⎞
lim ⎜1+ ⎟ = lim ⎜1+ ⎟ = e .
x→−∞
− ( x+ 1)
u→+∞
⎝ ⎠ ⎝ u⎠
u
x
.
bx
2x−1
⎛ a ⎞
5. Να υπολογιστούν τα όρια: (i) lim ⎜1+
⎟
x→+∞⎝ x ⎠ , όπου ab∈R , , (ii) ⎛ x + 1 ⎞
lim ⎜ ⎟ ,
x→+∞⎝
x − 2 ⎠

57
(iii)
⎛ 1 ⎞
lim ⎜1+
⎟
x→+∞⎝
x ⎠
x
2
bx
ln(1 + kx)
και (iv) lim .
x →0
x
⎛ bx
⎛ a ⎞ ⎞
⎛ a ⎞
ln 1
a
⎜ + ⎟ x
bx ln 1+
⎛ ⎞ ⎜⎝
⎠ ⎟ ⎜ ⎟
x
⎛
⎝ ⎠ ⎝ ⎠
⎛ a ⎞⎞
Λύση: (i) ⎜1+ ⎟ = e = e . Θα υπολογίσουµε το lim ⎜bxln ⎜1+
⎟⎟
⎝ x
x→+∞
⎠
⎝ ⎝ x ⎠⎠ .
1 ⎛ a⎞ a a ⎛ a⎞ a ax ⎛ a⎞
Έχουµε: 1− ≤ ln 1 1 1 ln 1 xln 1 a
a ⎜ + ⎟≤ + − ⇔ ≤ ⎜ + ⎟≤ ⇔ ≤ ⎜ + ⎟≤
.
x 0
1
x x x a x x >
+ ⎝ ⎠ + ⎝ ⎠ x+
a ⎝ x⎠
x
ax
⎛ ⎛ a ⎞⎞
Αλλά lim = a και εποµένως (κριτήριο παρεµβολής) lim ln 1
x
⎜x
⎜ + ⎟⎟=
a .
→+∞ x+
a
x→+∞⎝
⎝ x ⎠⎠
bx
⎛ ⎛ a ⎞⎞
⎛ a ⎞ ab
Άρα lim ⎜bxln ⎜1+ ⎟⎟=
ab και συνεπώς lim ⎜1+ ⎟ = e .
x→+∞⎝
⎝ x
x→+∞
⎠⎠
⎝ x ⎠
2x−1 2x− 4+ 3 2( x−2) 3
⎛ x+ 1⎞ ⎛ x− 2+ 3⎞ ⎛ 3 ⎞ ⎛ x+
1⎞
(ii) lim ⎜ ⎟ = lim ⎜ ⎟ = lim ⎜1+ ⎟ lim ⎜ ⎟ =
x→+∞ x 2 x→+∞ x 2 x→+∞ x 2 x→+∞
⎝ − ⎠ ⎝ − ⎠ ⎝ − ⎠ ⎝ x−2⎠
2u
⎛ 3 ⎞ 6
= lim ⎜1+ ⎟ = e , σύµφωνα µε το (i).
u= x−2→+∞ u→+∞⎝
u ⎠
x
2
2 ⎛ 1 ⎞
x ln⎜1+
⎟
⎝ x ⎠
1
1+ στη θέση του x, δίνει
x
⎛ 1 ⎞
(iii) Έχουµε ⎜1+ ⎟ = e . Η βασική µας ανισότητα, για
⎝ x ⎠
2
1 ⎛ 1 1 2 1
ln
x+ ⎞ x ⎛
x ln
x+
⎞
≤ ⎜ ⎟≤ ⇒ ≤ ⎜ ⎟
x + 1 ⎝ x ⎠ x x+
1 ⎝ x ⎠ . Άρα ⎛ 2 ⎛ x + 1⎞ ⎞
lim ⎜x
ln ⎜ ⎟⎟
=+∞
x→+∞⎝
⎝ x ⎠⎠
5.2.14(i)).
Εποµένως,
x
2
2 ⎛ 1 ⎞
1
x ln 1+
⎛ ⎞
⎜ ⎟
⎝ x ⎠
u
lim ⎜1 ⎟ lim e
lim e
x→+∞ x x→+∞ 2 ⎛ 1 ⎞ u→+∞
⎝ ⎠
u= x ln⎜1+ ⎟→+∞
⎝ x ⎠
+ = = =+∞.
(πρόταση
kx
(iv) Έχουµε: ln(1 kx)
kx
1+ kx ≤ + ≤
+
k
. Αν x → 0 , τότε x > 0 και εποµένως
1+ kx ≤
ln(1 + kx)
ln(1 + kx)
≤ ≤ k . Από το κριτήριο παρεµβολής παίρνουµε lim = k . Με τον ίδιο
x
x→0
+
x
ln(1 + kx)
τρόπο (αλλάζοντας φορά στις ανισότητες) παίρνουµε lim = k . Εποµένως
x→0
−
x
ln(1 + kx)
lim = k .
x →0
x
x
a
6. Να υπολογιστεί το όριο: lim , a > 0 .
x→±∞
x
a + 1
x
a 1
Λύση: Αν a = 1, τότε = για κάθε x∈R .
x
a + 1 2
x
Έστω 0< a < 1. Τότε lim a = 0 και lim a
x = +∞ (πρόταση 5.4.1 (ii)). Εποµένως,
x→+∞
x→−∞
x
x
lim a
1 lim u
0 a
u
= = και lim = lim = 1.
x→+∞
x
x
a + u= a →0
u→0
x
x
u+
1
x→−∞
a + 1 u= a →+∞ u→+∞
u+
1
x
x
a
a
Αν a > 1, πάλι µε βάση την πρόταση 5.4.1 βρίσκουµε ότι lim = 1 και lim = 0 .
x→+∞
x
x
a + 1
x→−∞
a + 1

58
n ⎛ x ⎞
7. Να δειχθεί ότι για κάθε x∈R , η ακολουθία cos ⎜ ⎟, n = 1,2, … τείνει στο 1.
⎝n
⎠
Απόδειξη: Για x = 0 , η ακολουθία είναι σταθερή (ίση µε 1). Υποθέτουµε ότι x ≠ 0 . Αν το n
2| x | x ⎛ π π ⎞
είναι αρκούντως µεγάλο (µεγαλύτερο από ), τότε ∈ ⎜ − , ⎟ και εποµένως,
π n ⎝ 2 2⎠
⎛ x ⎞
cos⎜
⎟ > 0 . Άρα ορίζεται ο λογάριθµος ln ⎛ n ⎛ x ⎞
cos ⎞ x
nln ⎛ ⎛ ⎞
⎜ ⎟=
⎜cos
⎟
⎞
⎝n
⎠
⎝ ⎜ ⎝n
⎟ ⎠⎠ ⎝ ⎜ ⎝n
⎟ ⎠⎠ .
Επειδή
cos
n
⎛ x ⎞
⎜ ⎟ = e
⎝n
⎠
⎛ ⎛ x ⎞⎞
nln⎜cos⎜
⎟⎟
⎝ ⎝n
⎠⎠
⎡ ⎛ ⎛ x ⎞⎞⎤
, αρκεί να δείξουµε ότι lim ⎢nln ⎜cos⎜
⎟⎟⎥
= 0 .
n→+∞
⎣ ⎝ ⎝n
⎠⎠⎦
x
⎛ ⎛ ln(cos )
Θέτουµε y = ⎯⎯⎯→ 0 . Τότε, ln cos x ⎞ ⎞
n
x
y
n→+∞
⎜ ⎜ ⎟⎟
= ⋅ .
n
⎝ ⎝n⎠⎠
y
⎡ ⎛ ⎛ x ⎞⎞⎤
ln(cos y)
Με βάση την πρόταση 5.2.17, lim ⎢nln ⎜cos⎜
⎟⎟⎥
= x⋅lim
.
n→+∞
n
y→0
⎣ ⎝ ⎝ ⎠⎠⎦
y
1
Σύµφωνα µε την ανισότητα της πρότασης 5.4.8, έχουµε 1− ≤ln(cos y) ≤cos y− 1.
cos y
cos y−1 ln(cos y) cos y−1
⎛cos y −1⎞
Αν y > 0, τότε ≤ ≤ . Επειδή lim⎜
⎟=
0 (πρόταση 5.1.17)
ycos
y y y
y→0
⎝ y ⎠
ln(cos y)
και limcos y = 1, από το κριτήριο παρεµβολής παίρνουµε lim = 0 . Αν y < 0 απλώς
y→0
y→0
+
y
αλλάζουµε φορά στην ανισότητα και παίρνουµε
⎡ ⎛ ⎛ x ⎞⎞⎤
εποµένως, lim ⎢nln ⎜cos⎜
⎟⎟⎥
= 0 .
n→+∞
⎣ ⎝ ⎝n
⎠⎠⎦
ln(cos y)
lim = 0 . Άρα
y
y→0
−
ln(cos y)
lim = 0 και
y→0
y
Άλυτες ασκήσεις
1. Αν xyab> , , , 0, ab≠ , 1 και
a
x y
= b και
x
b a
= y , να δειχτεί ότι:
a b a+
b
e + e
2
2. Να δείξετε ότι: > e , όπου ab∈ , R µε a ≠ b .
2
2 lnb−
lna
2
3. Αν 0 < a< b, να δείξετε ότι ≤ ≤ .
b b − a a
∞
4. Να δείξετε ότι η σειρά ∑ n(ln( n+ 1) −ln n)
δεν συγκλίνει.
n=
1
5. Έστω a
n
> 0 , για κάθε n = 0,1, 2, … Να δείξετε την ισοδυναµία: Η σειρά
∞
σειρά ∑ ln(1 + an
) συγκλίνει.
n=
0
a
⎛ x ⎞ ⎛ y ⎞
⎜ ⎟ = ⎜ ⎟ .
⎝logab⎠ ⎝logb
a⎠
x
e −1
6. Να υπολογίσετε τα όρια: (i) lim
x→1
x − 1
, (ii) lim ( ( ln( ) ln ))
e
x x+ a − x , (iii) lim
x→+∞
x→0
x
1
⎛ 1 ⎞
ln cos x
sin x
(iv) lim ⎜1+
x→+∞
n ⎟ µε n > 0 , (v) lim , (vi) lim(cos x)
.
2
⎝ x
0
⎠
x → x
x→0
b
∞
∑ an
συγκλίνει ⇔ η
n=
0
x
2
− cos x
,
2
x

59
Κυκλοµετρικές συναρτήσεις
Α) Τόξο ηµιτόνου
Θεωρούµε τη συνάρτηση του ηµιτόνου sin : R →− [ 1,1] . Γνωρίζουµε ότι η συνάρτηση αυτή
δεν είναι 1-1.
y
1
-2π -π -π/2 O
π
2π
-3π/2
π/2 3π/2
x
-1
⎡ π π ⎤
Ο περιορισµός της όµως στο διάστηµα ⎢−
,
2 2⎥
⎣ ⎦
είναι γνησίως αύξουσα συνάρτηση. Ας
συµβολίσουµε µε κεφαλαία SIN την καινούρια συνάρτηση (περιορισµό) για να την
ξεχωρίζουµε από τη συνάρτηση του ηµιτόνου, η οποία ορίζεται σ’ όλο το R .
y
1
y = SIN(x)
-π/2
Ο
π/2
x
-1
⎡ π π ⎤
Επειδή η συνάρτηση SIN : ⎢−
, →[ −1,1]
2 2⎥
⎣ ⎦
είναι γνησίως αύξουσα και επί του [ − 1,1]
(παρατήρηση 5.3.13), αυτή αντιστρέφεται.
Η αντίστροφη συνάρτηση συµβολίζεται µε arcsin ή καταχρηστικά µε
1
sin − .
Είναι δηλαδή
−1
⎡ π π ⎤
arcsin = sin :[ −1,1] → ⎢ − ,
2 2 ⎥
⎣ ⎦ .
y
π/2
Η παραπάνω συνάρτηση απεικονίζεται
y = sin -1 (x)
= arcsinx
1
y = sinx
στο διπλανό σχήµα µε την παχιά
κόκκινη γραµµή και η συνάρτηση
⎡ π π ⎤
y = sin x, x∈ ⎢ − ,
2 2 ⎥ µε την λεπτή
⎣ ⎦
-π/2
-1
Ο
-1
1
π/2 x
διακεκοµµένη µπλέ γραµµή.
-π/2

60
Σύµφωνα µε την πρόταση 5.3.17, η συνάρτηση
−1
sin είναι συνεχής.
4.4.10 Σηµείωση
Πρακτικά, αλλά και ουσιαστικά, ο ορισµός
της συνάρτησης
1
sin −
µας επιτρέπει να
βρίσκουµε την τιµή της σ’ ένα σηµείο
x∈[ − 1,1] , σκεφτόµενοι ως εξής: Ποια γωνία
⎡ π π ⎤
θ στο διάστηµα ⎢−
,
2 2⎥
έχει ηµίτονο το x;
⎣ ⎦
Έτσι έχουµε:
−1
sin ( 1)
sin
π
− =− ,
2
⎛ −1 2 ⎞
sin
π
⎜
− =−
2 ⎟
,
⎝ ⎠ 4
−1
sin (0) 0
= ,
π
⎜
− =−
2 ⎟
,
⎝ ⎠ 3
⎛ −1 3 ⎞
−1 ⎛ 1 ⎞ π
sin ⎜− ⎟=−
,
⎝ 2⎠
6
−1 ⎛1
⎞ π
sin =
1 2
⎜ ⎟ , sin
⎛ − ⎞ ⎝2⎠
6 2 = π
⎜
⎟
,
⎝ ⎠ 4
sin
−1
π
⎜
2 ⎟
, sin (1) = .
⎝ ⎠ 3
2
⎛ 1 3 ⎞ − = π
y
1 π/2 rad
3 /2
2 /2
1/2
π/3 rad
π/4 rad
π/6 rad
O
0rad
-1/2
-π/6 rad
- 2/2
-π/4 rad
- 3/2
-π/3 rad
-1 -π/2 rad
x
Β) Τόξο συνηµιτόνου
Παρόµοια, ξεκινώντας κανείς από τη συνάρτηση του συνηµιτόνου,
y
1
-5π/2
-2π
-3π/2
-π
-π/2
O
π/2
π 5π/2
3π/2 2π
x
-1
θεωρεί τον περιορισµό της στο διάστηµα [ 0, π ] ,
y
1
O
π/2
π
x
-1
που είναι γνησίως φθίνουσα και επί του [ − 1,1] και άρα αντιστρέψιµη συνάρτηση.

61
Η αντίστροφη του περιορισµού συµβολίζεται µε arccos ή καταχρηστικά µε
1
cos −
και είναι
και αυτή συνεχής συνάρτηση.
Η παραπάνω συνάρτηση
y
π
απεικονίζεται στο σχήµα µε
την παχιά κόκκινη γραµµή και
η συνάρτηση y = cos x,
[ 0, π ]
x∈ µε την λεπτή
διακεκοµµένη µπλέ γραµµή.
5.4.11 Σηµείωση
Και εδώ, για να βρούµε την τιµή της συνάρτησης
1
cos − σ’ ένα σηµείο x∈[ − 1,1] ,
σκεφτόµαστε ως εξής: Ποια γωνία θ στο διάστηµα [ 0, π ] έχει συνηµίτονο το x; Έτσι έχουµε:
−1
cos (1) 0
1 3
= , cos
⎛ − ⎞ 2 = π
⎜
⎟
,
⎝ ⎠ 6
1 2
cos
⎛ ⎞ − 2 = π −1 ⎛1
⎞ π
⎜
⎟
, cos ⎜ ⎟ = ,
⎝ ⎠ 4 ⎝2⎠
3
−1
π −1 ⎛ 1⎞
2π
cos (0) = , cos ⎜− ⎟=
,
2 ⎝ 2⎠
3
1 2 3
cos
⎛ ⎞
− π 1 3 5
⎜
− =
2 ⎟
, cos
⎛ − π
⎞
⎝ ⎠ 4 ⎜
− =
2 ⎟
,
⎝ ⎠ 3
−1
cos ( − 1) = π .
y = cos -1 (x)
= arccosx
-1
π rad
-1
3π/4 rad
5π/6 rad
3
2
1
O
-1
2π/3 rad
2
2
π/2
1
y
1 Ο
2
π/2
y = cosx
π/2 rad
1
2
2
2
3
2
π
π/3 rad
π/4 rad
π/6 rad
0 rad
1 x
x
5.4.12 Παράδειγµα
Να αποδειχθεί ότι, για κάθε x∈[ − 1,1] ισχύει η σχέση:
sin
π
x+ cos x= .
2
−1 −1
−1
Απόδειξη: Έστω θ = sin x . Από τον ορισµό της συνάρτησης
1
sin − προκύπτει ότι sinθ = x
και −π /2 ≤θ ≤ π /2. Εποµένως, π ≥π / 2 −θ
≥ 0 . Για τη γωνία π /2− θ παρατηρούµε ότι
cos( π / 2 − θ) = sinθ
= x . Εφόσον π /2 −θ∈ [0, π]
, έπεται ότι
π
− θ = ⇔
−1
/2 cos x
θ
π
−1
+ cos x = / 2 , ήτοι
−1 −1
sin cos / 2
x+ x= π .

62
Γ) Τόξο εφαπτοµένης
y
Εδώ θεωρούµε τον βασικό κλάδο της εφαπτοµένης, δηλαδή τη
⎛ π π ⎞
συνάρτηση y = tan x, x∈ ⎜ − , ⎟ . Ο κλάδος αυτός είναι
⎝ 2 2 ⎠
γνησίως αύξουσα συνάρτηση.
Η αντίστροφη του περιορισµού συµβολίζεται µε arctan ή
καταχρηστικά µε
1
tan − .
π/2
-π/2
− − ,.
O
y
y = tan -1 x
π/2
-π/2
π/2
Ο
x
-π/2
y = tanx
−1
π
−1
π
lim tan x = και lim tan x =− .
x→+∞
2 x→−∞
2
ε π
δ > γιατί π /2 ε ( 0, π /2)
⎛π
⎜
⎝ 2
1
tan −
Η συνάρτηση αυτή απεικονίζεται στο σχήµα µε την παχιά κόκκινη γραµµή και η συνάρτηση
⎛ π π ⎞
y = tan x, x∈ ⎜ − , ⎟ µε την λεπτή διακεκοµµένη µπλέ γραµµή.
⎝ 2 2⎠ Από τη γραφική παράσταση παρατηρούµε ότι
< , οπότε π /2 ε ( 0, π /2)
*[Πράγµατι, έστω ε > 0 . Μπορούµε να υποθέσουµε ότι /2
− ∈ .
⎛π
⎞
⎞
Έστω δ = tan ⎜ − ε⎟>
0 . (Είναι 0 − ∈ και άρα tan − ε ⎟>
0 ).
⎝ 2 ⎠
⎠
1
Άρα
π ε −
− = tan δ . Επειδή η συνάρτηση είναι γνησίως αύξουσα, θα έχουµε για κάθε
2
⎛ π ⎞
x∈ ⎜ δ , ⎟
⎝ 2 ⎠ : π −1 1 π
> tan x > tan δ = ε
2
2
x

63
Έχουµε, δηλαδή δείξει ότι για κάθε ε > 0, υπάρχει δ > 0, τέτοιο ώστε
π
2
−1
π
> tan x > ε 2
− ,
για κάθε x
> δ .
y
ε
π/2
Ο
δ
x
-π/2
−1
π
Εποµένως lim tan x = . ]
x→+∞
2
−1
π
Η σχέση lim tan x = − αποδεικνύεται µε παρόµοιο τρόπο.
x→−∞
2
∆) Τόξο συνεφαπτοµένης
Εδώ αντιστρέφουµε τον κλάδο της συνεφαπτοµένης
y = cot x, x∈ [ 0, π ] .
y
y = cotx
π
y = cot -1 x
π/2
O
π/2
π
x
Παίρνουµε έτσι µια γνησίως φθίνουσα συνάρτηση, η οποία απεικονίζεται στο σχήµα µε την
παχιά κόκκινη γραµµή. Όπως στην περίπτωση της
−1
lim cot x 0
x→+∞
= και
lim cot
x→−∞
−1
x = π .
1
tan − , µπορούµε να αποδείξουµε ότι
5.4.13 Παραδείγµατα
1. Να βρεθούν τα πεδία ορισµού και τα σύνολα τιµών των συναρτήσεων:
−1 x −1
(i) y = tan
x + 1
και (ii) −1
y = cos (sin x)
.

64
Λύση: (i) Θα πρέπει
x −1 ≥ 0
x + 1
συνάρτησης είναι λοιπόν το σύνολο ( −∞, −1) ∪ [1, +∞ ).
και x ≠ − 1. Άρα x < − 1 ή x ≥ 1. Το πεδίο ορισµού της
Παρατηρούµε ότι η συνάρτησή µας είναι η σύνθεση
g :( −∞, −1) ∪ [1, + ∞)
→ R η συνεχής συνάρτηση µε τύπο
gx ( ) =
tan
− 1
g , όπου
x −1
. Για να βρούµε το
x + 1
σύνολο τιµών της συνάρτησής µας θα βρούµε πρώτα το σύνολο τιµών της g.
x −1
Έστω y =
x + 1
. Τότε y ≥ 0.
Επίσης 2 x −1
2 2
y = ⇒(1 − y ) x= y + 1 .
x + 1
2
y + 1
2
Αν y = 1, τότε 0= 2, άτοπο. Άρα y ≠ 1. Τότε x = . Αν 0≤
y < 1, τότε 1≥1− y > 0
2
1 − y
2 2
1
2 2 y
και εποµένως 1≤ . Επίσης 0≤ y ⇒1≤ y + 1. Άρα
+ 1 1 y 1
≥ = 1⇒
+ ∈ [1, +∞ ) .
1− y
2
2 2
1−
y 1 1−
y
2 2 2
2
Αν y > 1, τότε 1− y < 0. Εποµένως,
y + 1 1− y − 2 2 1
1 1
y +
= − =− +

65
−1
sin x
−1
2−
lim
−1
2x−
sin x x→0
(ii) lim
x sin x
=
. Το lim το υπολογίσαµε ίσο µε 1. Τώρα, θέτουµε
x→0
−1
−1
2x+
tan x tan x x →0
x
2+
lim
x→0
x
−1
−1
tan x y
y = tan x→ 0 και εποµένως x = tan y . Άρα lim = lim = 1. Εποµένως
x→0 x y→0
tan y
−1
2x−sin x 2−1 1
lim = =
x→0
2 tan
−1
x+ x 2 + 1 3
.
x + 1
1−
2y
(iii) Θέτουµε y = ⎯⎯⎯→ 1. Τότε x =
x→+∞
x + 2
y − 1
. Εποµένως ⎛ ⎛ −1 x + 1 π ⎞⎞
lim ⎜x⎜tan
− ⎟⎟=
x→+∞⎝
⎝ x + 2 4⎠⎠
⎛1− 2y
⎛ −1
π ⎞⎞
−1 π
−1
π
= lim⎜
⎜tan
y − ⎟⎟. Τέλος, θέτουµε u = tan y− →tan (1) − = 0 . Εποµένως
y→1
⎝ y −1 ⎝ 4⎠⎠
4 4
⎛ π ⎞ 1+
tanu
y = tan ⎜u+ ⎟=
. Άρα 1 − 2 y 3tan u+
=−
1 .
⎝ 4⎠
1−
tanu
y−1 2tanu
⎛1− 2y⎛ 1
3tanu 1 1
u
Συνεπώς lim tan y π − ⎞⎞
⎛ + ⎞
⎜ ⎜ − ⎟⎟=− lim⎜ u⎟=− lim(3tan u+ 1) ⋅ lim =
y→1 y 1 4 u→0 2tanu 2 u→0 u→0
⎝ − ⎝ ⎠⎠
⎝ ⎠
tanu
1 1
=− lim(3⋅ 0 + 1) ⋅ 1 =− .
2 u→0
2
Άλυτες ασκήσεις
1. Να υπολογίσετε τα όρια: (i)
π − 2cos
lim
x→0
x −
−1
−1
tan 2
x
, (ii)
x
⎛ ⎛ x+ 1 x ⎞⎞
lim x tan tan
−1 −1
⎜ ⎜ − ⎟⎟
x→+∞
⎝ ⎝ x+ 2 x+
2⎠⎠ .
(Υπόδειξη: Για το (ii) αφαιρέστε και προσθέστε το 4
π και στη συνέχεια υπολογίστε τα δύο όρια, όπως
στο παράδειγµα 5.4.13.iii).
5.5 Παράρτηµα του κεφαλαίου 5*
Αποδείξεις των θεωρηµάτων Bolzano και µέγιστης-ελάχιστης τιµής
Πρόταση: Έστω f :
στο σηµείο
ξ ∈ A. Τότε έχουµε:
A→ R µια συνάρτηση, όπου A⊆ R . Υποθέτουµε ότι η f είναι συνεχής
i) Αν f ( ξ ) > 0, τότε υπάρχει δ > 0 , τέτοιο ώστε, για κάθε x∈ A µε | x − ξ | < δ να ισχύει
f( x ) > 0.
ii) Αν f ( ξ ) < 0, τότε υπάρχει δ > 0 , τέτοιο ώστε, για κάθε x∈ A µε | x − ξ | < δ να ισχύει
f( x ) < 0.

66
f ( ξ )
Απόδειξη: i) Έστω ε = > 0 . Εφόσον lim f ( x) = f( ξ ) , υπάρχει δ > 0 τέτοιο ώστε
2
x→ξ
f ( ξ )
| f( x) − f( ξ)|
< ε = , για κάθε x∈ A µε | x − ξ | < δ . Από τη σχέση όµως
2
f ( ξ )
f( ξ) f( ξ)
| f( x) − f( ξ )| < προκύπτει − < f( x) − f( ξ ) ⇔ f( x) > > 0.
2
2 2
ii) Η σχέση f ( ξ ) < 0 είναι ισοδύναµη µε τη − f ( ξ ) > 0. Τώρα εφαρµόζουµε το (i) για τη
συνάρτηση − f . ■
Θεώρηµα του Bolzano: Θεωρούµε µια συνεχή συνάρτηση f :[ a, b]
→ R . Υποθέτουµε ότι οι
τιµές της στα άκρα του διαστήµατος [ ab , ] είναι ετερόσηµες, δηλαδή f( a) f( b ) < 0.
Τότε, η συνάρτηση f έχει µια τουλάχιστον ρίζα στο διάστηµα ( ab , ).
Απόδειξη: Υποθέτουµε αρχικά ότι f( a ) < 0 και f( b ) > 0. Θεωρούµε το σύνολο
A= { t∈ [ a, b]|
f ( x) < 0 για κάθε x∈ [ a, t]}
. Παρατηρούµε ότι a∈
A. (Το κλειστό διάστηµα
[ aa , ] είναι το µονοσύνολο {} a ). Το Α περιέχεται στο διάστηµα [ ab , ] και συνεπώς είναι άνω
φραγµένο από το b. Ας είναι ξ το supremum του Α. Παρατηρούµε ότι t∈
A, για κάθε
a≤ t < ξ . Πράγµατι, εφόσον ξ = sup A, υπάρχει t′∈ A µε t < t′
< ξ . Άρα f( x ) < 0 για κάθε
x∈ [ at′ , ]. Ειδικότερα, f( x ) < 0 για κάθε x∈ [ at , ], ήτοι t∈ A.
Θα αποδείξουµε ότι το ξ είναι ζητούµενη ρίζα. Θα αποκλείσουµε τις περιπτώσεις f ( ξ ) < 0
και f ( ξ ) > 0.
(i) Έστω ότι f ( ξ ) < 0.
y
Προφανώς
ξ < b . Εφόσον η f είναι συνεχής
στο ξ , υπάρχει διάστηµα ( ξ − δξ , + δ)
µε
ξ+δ
f( x ) < 0 για κάθε x∈( ξ − δξ , + δ) ∩ [ ab , ],
σύµφωνα µε την προηγούµενη πρόταση.
Μπορούµε να επιλέξουµε το δ ώστε
δ < b − ξ , οπότε [ ξ, ξ + δ) ⊆ [ ab , ].
⎡ δ ⎤
Επειδή η f παίρνει αρνητικές τιµές στα διαστήµατα [ a, ξ ] και ⎢ξ,
ξ + ⊆
2 ⎥ [ ξ, ξ + δ)
, η f
⎣ ⎦
⎡ δ ⎤
παίρνει αρνητικές τιµές σ’ όλο το διάστηµα ⎢a,
ξ +
2 ⎥
⎣ ⎦ .
δ
δ
Εποµένως ξ + ∈ A και συνεπώς ξ + ≤ ξ = sup A, άτοπο.
2
2
(ii) Έστω ότι f ( ξ ) > 0.
O
a
δ/2
ξ
δ
ξ+
2
b
x

67
Προφανώς
ξ > a . Όπως προηγουµένως, συµπεραίνουµε ότι υπάρχει διάστηµα
( ξ −δξ
, ] ⊆ [ ab , ] στο οποίο η f παίρνει θετικές τιµές.
y
⎛ δ ⎞
Επειδή η f ⎜ξ
− ⎟>
0 , θα είναι
⎝ 2 ⎠
δ
ξ − ≥ ξ = sup A, άτοπο.
2
ξ- δ
Η περίπτωση f( a ) > 0 και f( b ) < 0
αντιµετωπίζεται παρόµοια. ■
O
a
δ/2
ξ
b
x
δ
ξ-
2
Πρόταση: Θεωρούµε µια συνάρτηση f :[ a, b]
→ R . Υποθέτουµε ότι η f είναι συνεχής. Τότε η f
είναι φραγµένη.
Απόδειξη: Θα κινηθούµε όπως στην απόδειξη του θεωρήµατος του Bolzano. Θεωρούµε το
σύνολο A = { t ∈[
a,
b]
| η f είναι φραγµένη στο διάστηµα [ a , t]}
.
Προφανώς
a ∈ A και εποµένως το Α δεν είναι κενό. Εφόσον το Α είναι άνω φραγµένο από
το b, έχει ελάχιστο άνω φράγµα ξ.
Ισχυρισµός 1: ξ ∈ A .
Αν ξ = a , τότε προφανώς ξ ∈ A . Έστω a < ξ . Επειδή lim f ( x) = f( ξ ) υπάρχει διάστηµα
x→ξ
−
( ξ − δ , ξ ] ⊆ [ a,
b]
, στο οποίο η f είναι φραγµένη. (Πράγµατι, υπάρχει δ > 0 µε την ιδιότητα
| f( x) − f( ξ )| < 1 ⇒ | f( x)| < 1 + | f( ξ )|). Έστω t ∈ A µε ξ − δ < t < ξ . Εφόσον η f είναι
φραγµένη στα διαστήµατα [ a , t]
και [ t , ξ ] , θα είναι φραγµένη σ’ όλο το διάστηµα [ a , ξ ] ,
δηλαδή ξ ∈ A .
Ισχυρισµός 2: ξ = b .
Έστω ότι ξ < b . Εφόσον lim f ( x)
= f ( ξ ) , υπάρχει διάστηµα [ ξ , ξ + δ ) ⊆ [ a,
b]
στο
x→ξ
+
οποίο η f είναι φραγµένη. Εφόσον η f είναι φραγµένη στα διαστήµατα [ a , ξ ] και
⎡ δ ⎤
⎡ δ ⎤ δ
⎢ξ , ξ +
⎣ 2 ⎥ , θα είναι φραγµένη σ’ όλο το διάστηµα
⎦
⎢a , ξ +
⎣ 2 ⎥ . Άρα ξ + ∈ A και
⎦ 2
δ
εποµένως ξ + ≤ ξ = sup A , άτοπο. ■
2
Θεώρηµα µέγιστης-ελάχιστης τιµής: Θεωρούµε µια συνεχή συνάρτηση f :[ a, b]
→ R . Τότε η
f παίρνει µέγιστη και ελάχιστη τιµή, δηλαδή αν M = sup{ f ( x)
| x ∈[
a,
b]}
και
m = inf{ f ( x)
| x ∈ [ a,
b]}
, τότε υπάρχουν x x ∈ [ a,
] µε f ( x 1
) = M και f ( x 2
) = m .
1, 2
b

68
Απόδειξη: Υποθέτουµε ότι M > f (x)
για κάθε x ∈ [ a,
b]
. Θεωρούµε τη συνάρτηση
1
g:[ a, b]
→ R µε g(
x)
= M − f ( x)
για κάθε x ∈ [ a,
b ] . Η g είναι συνεχής στο διάστηµα
[ a , b]
και εποµένως φραγµένη. Έστω λ ένα άνω φράγµα της g.
Επειδή M = sup{ f ( x)
| x ∈[
a,
b]}
, υπάρχει ακολουθία x ) σηµείων του διαστήµατος
[ a , b]
µε
για κάθε
1
1
M − f ( xn
) < , για κάθε n = 1,2, … Εποµένως λ > g(
xn ) =
> n ,
n
M − f ( x )
n = 1,2, … , δηλαδή η ακολουθία των θετικών ακεραίων είναι άνω φραγµένη,
άτοπο.
Για το m = inf{ f ( x)
| x ∈ [ a,
b]}
, παρατηρούµε ότι m = −sup{
− f ( x)
| x ∈[
a,
b]}
. ■
( n
n