F. Krause - Universität Potsdam

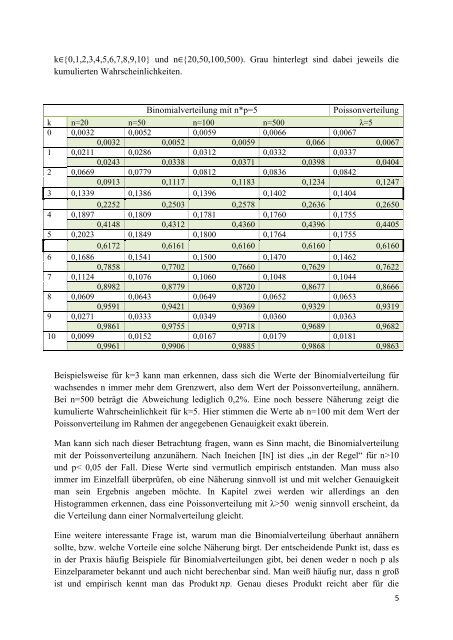
k {0,1,2,3,4,5,6,7,8,9,10} und n {20,50,100,500). Grau hinterlegt sind dabei jeweils die
kumulierten Wahrscheinlichkeiten.
Binomialverteilung mit n*p=5
Poissonverteilung
k n=20 n=50 n=100 n=500 λ=5
0 0,0032 0,0052 0,0059 0,0066 0,0067
0,0032 0,0052 0,0059 0,066 0,0067
1 0,0211 0,0286 0,0312 0,0332 0,0337
0,0243 0,0338 0,0371 0,0398 0,0404
2 0,0669 0,0779 0,0812 0,0836 0,0842
0,0913 0,1117 0,1183 0,1234 0,1247
3 0,1339 0,1386 0,1396 0,1402 0,1404
0,2252 0,2503 0,2578 0,2636 0,2650
4 0,1897 0,1809 0,1781 0,1760 0,1755
0,4148 0,4312 0,4360 0,4396 0,4405
5 0,2023 0,1849 0,1800 0,1764 0,1755
0,6172 0,6161 0,6160 0,6160 0,6160
6 0,1686 0,1541 0,1500 0,1470 0,1462
0,7858 0,7702 0,7660 0,7629 0,7622
7 0,1124 0,1076 0,1060 0,1048 0,1044
0,8982 0,8779 0,8720 0,8677 0,8666
8 0,0609 0,0643 0,0649 0,0652 0,0653
0,9591 0,9421 0,9369 0,9329 0,9319
9 0,0271 0,0333 0,0349 0,0360 0,0363
0,9861 0,9755 0,9718 0,9689 0,9682
10 0,0099 0,0152 0,0167 0,0179 0,0181
0,9961 0,9906 0,9885 0,9868 0,9863
Beispielsweise für k=3 kann man erkennen, dass sich die Werte der Binomialverteilung für
wachsendes n immer mehr dem Grenzwert, also dem Wert der Poissonverteilung, annähern.
Bei n=500 beträgt die Abweichung lediglich 0,2%. Eine noch bessere Näherung zeigt die
kumulierte Wahrscheinlichkeit für k=5. Hier stimmen die Werte ab n=100 mit dem Wert der
Poissonverteilung im Rahmen der angegebenen Genauigkeit exakt überein.
Man kann sich nach dieser Betrachtung fragen, wann es Sinn macht, die Binomialverteilung
mit der Poissonverteilung anzunähern. Nach Ineichen [IN] ist dies „in der Regel“ für n>10
und p< 0,05 der Fall. Diese Werte sind vermutlich empirisch entstanden. Man muss also
immer im Einzelfall überprüfen, ob eine Näherung sinnvoll ist und mit welcher Genauigkeit
man sein Ergebnis angeben möchte. In Kapitel zwei werden wir allerdings an den
Histogrammen erkennen, dass eine Poissonverteilung mit λ>50 wenig sinnvoll erscheint, da
die Verteilung dann einer Normalverteilung gleicht.
Eine weitere interessante Frage ist, warum man die Binomialverteilung überhaut annähern
sollte, bzw. welche Vorteile eine solche Näherung birgt. Der entscheidende Punkt ist, dass es
in der Praxis häufig Beispiele für Binomialverteilungen gibt, bei denen weder n noch p als
Einzelparameter bekannt und auch nicht berechenbar sind. Man weiß häufig nur, dass n groß
ist und empirisch kennt man das Produkt . Genau dieses Produkt reicht aber für die
5