Lösung - Stempel-unterricht.de

Wilhelmi Gymnasium SinsheimMathematikkurs V4 – Klausur 11.3 – Lösung25. April 20131. AufgabeBestimmen Sie zur Funktion die Integralfunktion .∫2. AufgabePrüfen Sie, ob die nach rechts bzw. nach links geöffnete Fläche einen endlichen oderunendlichen Flächeninhalt hat.∫∫ ( )fürfür∫Der Flächeninhalt ist endlich.∫∫ ( )fürDer Flächeninhalt ist unendlich.für3. AufgabeBerechnen Sie den Mittelwert der rechts abgebildetenFunktion im Intervall . Stellen Sieden Mittelwert graphisch dar.̅Aus dem Graphen kann man erkennen, dassist. Für den Mittelwert gilt:̅∫∫ ( )[ ]( )Viel Erfolg

Wilhelmi Gymnasium SinsheimMathematikkurs V4 – Klausur 11.3 – Lösung25. April 20134. AufgabeBerechnen Sie den Inhalt der Fläche, die von den Graphen der Funktion und mitund eingeschlossen wird.Um die eingeschlossene Fläche zu berechnen, müssen die Schnittpunkte bestimmt werden:Dies ist für und erfüllt. Die Fläche berechnet sich somit wie folgt:∫ ∫ [ ]( )Der Flächeninhalt beträgt FE.5. AufgabeLösen Sie die Gleichung – .Nach dem Satz des Nullprodukts, müssen entweder oder null werden. Dafür alle ergeben sich folgende Lösungen:6. AufgabeGegeben sind die Funktionena) Zeigen Sie, dass sich alle Graphen in einem Punkt schneiden und dort dieselbe Steigunghaben.Um dies zu zeigen setzt man zwei Graphen aus der Funktionsschar gleich null undzeigt, dass ihr Schnittpunkt unabhängig von ist.Da und ungleich sind ist die Gleichung nur für erfüllt. Da unabhängigvon ist ist gezeigt, dass sich alle Graphen in einem Punkt schneiden.Zur Bestimmung der Steigung setzt man in die Ableitung von ein:Somit haben alle Funktionen der Schar die Steigung .Viel Erfolg

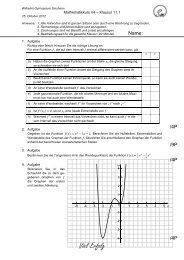
Wilhelmi Gymnasium SinsheimMathematikkurs V4 – Klausur 11.3 – Lösung25. April 2013b) Skizzieren Sie den Graphen fürc) Zeigen Sie, dass alle Extrempunkte der Kurvenschar zuauf der Parabel mitliegen.Bestimmung der Extrempunkte:( ) ( ) ( )Ersetzt man nun durch so folgt:7. AufgabeWahr oder falsch? Kreuzen Sie an.a) Der Graph einer gebrochenrationalen Funktion besitzt an derStelle eine senkrechte Asymptote, wenn Nullstelle desNenners und keine Nullstelle des Zählers ist.b) Der Graph einer gebrochenrationalen Funktion hat eine waagerechteAsymptote, falls der Grad des Zählers gleich demGrad des Nenners ist.c) Der Graph einer ganzrationalen Funktion dritten Grades hatmindestens drei Nullstellen.d) Hat eine Funktion drei Nullstellen, so hat Sie mindestens zweiExtremstellen.wahrxxxfalschxViel Erfolg

Wilhelmi Gymnasium SinsheimMathematikkurs V4 – Klausur 11.3 – Lösung25. April 20138. AufgabeGegeben ist die Funktionvon an.. Ihr Schaubild ist . Geben Sie die Asymptotenauf Polstellen (Nullstelle des Nenner-Für die senkrechte Asymptote untersucht manterms ist nicht Nullstelle des Zählerterms):ist also Polstelle von , somit hat an der Stelle eine senkrechteAsymptote.Für waagerechte Asymptoten untersucht man das Verhalten von für .Der Grad des Zählerterms ist gleich dem Grad des Nennerterms, deshalb gehtgegeneine waagerechte Asymptote. Die waagerechte Asymptote liegt bei9. AufgabeDie nebenstehende Abbildung zeigt denGraphen der Funktion .Bestimmen Sie die Werte für und .( )Die Funktion ist gegenüber der Sinusfunktionum nach oben verschobenAußerdem ist die Funktion um nach rechts verschoben gegenüber der ursprünglichenSinusfunktion . Daraus ergibt sich ein Schnittpunkt mit der -Achse am Punkt. Die gegebene Funktion ist allerdings um eins nach links rechtsverschobenDarausViel Erfolg

Wilhelmi Gymnasium SinsheimMathematikkurs V4 – Klausur 11.3 – Lösung25. April 201310. AufgabeDie vier Abbildungen zeigen Schaubilder von Funktionen einschließlich aller waagerechtenAsymptoten.Eines dieser Schaubilder gehört zu der Funktion mit .Abbildung 3 Abbildung 4a) Begründen Sie, dass Abbildung 2 zu der Funktion gehört. Bestimmen Sie den Wertvonist achsensymmetrisch und hat beider Graph in Abbildung 2 erfüllte dies.eine waagerechte Asymptote. NurBerechnung von a:b) Von den anderen drei Abbildungen gehört eine zu der Ableitungsfunktion und einezu der Integralfunktion mit ∫ Begründen Sie zu welcher Abbildungdie entsprechende Funktion gehört.Für die Ableitung gilt:Für ist und Für ist . Außerdem hat an der Stelleeine Nullstelle (da an der Stelle ein Maximum hat). Diese Bedingungenerfüllt nur Abbildung 3.Für die Integralfunktion gilt, dass sie an der Stellegleich null ist, denn:∫Dies erfüllt nur Abbildung 4Viel Erfolg

Wilhelmi Gymnasium SinsheimMathematikkurs V4 – Klausur 11.3 – Lösung25. April 201311. AufgabeEin Medikament wird in unterschiedlicher Wirkstoffdosierung hergestellt. Durch die Funktionmit wird die Konzentration dieses Medikamentenwirkstoffs imBlut eines Patienten beschrieben. Der Parameter berücksichtigt die Höhe derWirkstoffdosierung.Dabei wird die Zeit in Stunden siet der Einnahme und die Wirkstoffkonzentrationim Blut in Milligramm pro Litergemessen.a) Die Wirkstoffkonzentration im Blut des Patienten beträgt vier Stunden nach der Einnahme. Berechne den Parameter .Es gilt:Der Parameter beträgt .b) Skizzieren Sie den Graphen der Funktion für die ersten Stunden nach der Einnahme.Viel Erfolg

Wilhelmi Gymnasium SinsheimMathematikkurs V4 – Klausur 11.3 – Lösung25. April 2013c) Wie hoch ist für die mittlere Wirkstoffkonzentration des Medikaments in denersten Stunden?Für die mittlere Konzentration gilt:̅∫Die mittlere Wirkstoffkonzentration beträgt .d) Damit das Medikament wirksam ist, sollte die Wirkstoffkonzentration im Blut mindestensbetragen. Wie lange ist dies bei der Dosierung der Fall?Mithilfe des GTRs bestimmt man den Schnittpunkt von undundDie Dosierung von besteht eine halbe Stunde nach Einnahme des Medikamentsund hält etwa Stunden an.e) Zu welchem Zeitpunkt wird das Medikament für am stärksten abgebaut?(das Extremum der Ab-Mithilfe des GTRs bestimmt man den Wendepunkt vonleitung von ):Die Dosierung nimmtStunden nach Einnahme des Medikaments am stärksten ab.f) Zeigen Sie, dass die Wirkstoffkonzentration unabhängig vom Parameter vier Stundennach der Einnahme maximal ist.Man setzt in die Ableitung von ein und zeigt, dass dort ein Maximum vorliegt,welches unabhängig von ist:( )Damit ist unabhängig von immer gleich null.( )g) Weisen Sie nach, dass die Funktion mit eine Stammfunktionvon ist.Viel Erfolg

Wilhelmi Gymnasium SinsheimMathematikkurs V4 – Klausur 11.3 – Lösung25. April 2013h) Um eine Gefährdung des Patienten auszuschließen sollte eine Wirkstoffkonzentrationvon mehr alsvermieden werden. Ermitteln Sie die Dosierung , die nicht überschrittenwerden sollte.Das Maximum von soll an der Stelle nicht größer als sein:Es sollte eine Dosierung vonnicht überschritten werden.ZusatzaufgabeAuch Kegel, Kegelstumpf, und Kugel sind rotationssymmetrische Körper. Leiten Sie mithilfeder Integralformel für das Rotationsvolumen die Formel für das Volumen eines Kegels() her.Für das Volumenintegral gilt:∫( )lässt sich aus dem Schaubild des Kegels bestimmen:Die Grenzen des Kegels und damit des Integrals gehen vondas Volumenintegral:bis . Damit ergibt sich für∫ ( ) ∫ * + * +Viel Erfolg