Leseprobe 300332

Die Größe jedes dieser Unterteile hängt von der Beschränkung des Druckers ab und kann im Algorithmus als Eingangsparameter
angegeben werden.
ss UUUUUUUUUUUUUUUUUU =
ss BBBBBBBBBBBBBB
ss MMMMMMMMMMMMMMMMMMMMMMMMMMMMh
Daraufhin wird jedes Unterteil einzeln und unabhängig voneinander weiterverarbeitet. Dazu werden jeweils die nicht
zusammenhängenden Punktwolken mit einem Greedy Flächentriangulationsalgorithmus in Flächen gewandelt [13].
Diese zwei unverbundenen Flächen müssen im weiteren Verlauf an ihren Randbereichen geschlossen werden, um
ein druckbares Volumenmodell zu ermitteln. In [10] ist detaillierter beschrieben, wie weitere Prozessschritte nicht
gewünschte Bereiche aus dem Volumenmodell entfernen können. Dies können beispielsweise Bereiche in dem Modell
sein, die unterhalb der Festshimgrenze liegen und somit mit Flüssigshim gefüllt werden können. Dadurch werden
nur Regionen gedruckt, die laut Anforderung und Materialspezifikation als Festshim in den Fügespalt eingeführt werden
sollen. Das Schließen der Flächen zu einem Volumenmodell erfolgt mittels dynamischer Polygonerzeugung an
den Flächenkonturen. Dazu werden im ersten Schritt alle Konturpunkte I1 und I2 der Flächen durch einen Grenzpunktextraktionsalgorithmus
ermittelt. Die Anzahl der Konturpunkte der oberen und unteren Wolke muss für die weitere
Verarbeitung identisch sein, weshalb erneut ein k-nächste-Nachbarn Algorithmus mit k=1 angewendet wird,
wobei die Konturpunkte der oberen Wolke als Suchpunkte eingesetzt werden. Sollte die obere Punktwolke eine
höhere Punktdichte aufweisen als die untere, würde nicht jeder Konturpunkt mit der anderen Wolke über ein Polygon
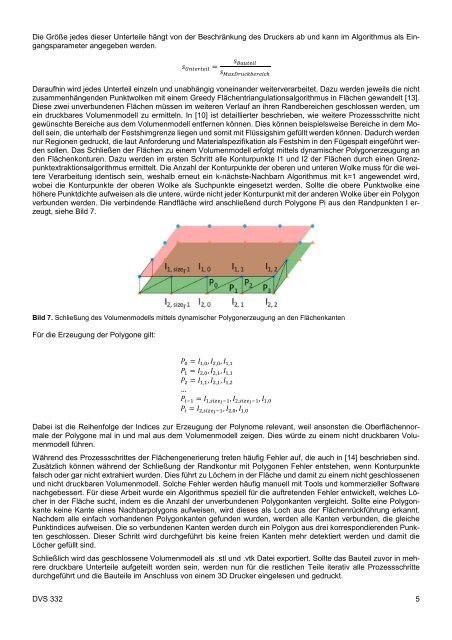
verbunden werden. Die verbindende Randfläche wird anschließend durch Polygone Pi aus den Randpunkten I erzeugt,
siehe Bild 7.
Bild 7. Schließung des Volumenmodells mittels dynamischer Polygonerzeugung an den Flächenkanten
Für die Erzeugung der Polygone gilt:
PP 0 = II 1,0 , II 2,0 , II 1,1
PP 1 = II 2,0 , II 2,1 , II 1,1
PP 2 = II 1,1 , II 2,1 , II 1,2
…
PP ii−1 = II 1,sssssseeII −1, II 2,sssssseeII −1, II 1,0
PP ii = II 2,sssszzeeII −1, II 2,0 , II 1,0
Dabei ist die Reihenfolge der Indices zur Erzeugung der Polynome relevant, weil ansonsten die Oberflächennormale
der Polygone mal in und mal aus dem Volumenmodell zeigen. Dies würde zu einem nicht druckbaren Volumenmodell
führen.
Während des Prozessschrittes der Flächengenerierung treten häufig Fehler auf, die auch in [14] beschrieben sind.
Zusätzlich können während der Schließung der Randkontur mit Polygonen Fehler entstehen, wenn Konturpunkte
falsch oder gar nicht extrahiert wurden. Dies führt zu Löchern in der Fläche und damit zu einem nicht geschlossenen
und nicht druckbaren Volumenmodell. Solche Fehler werden häufig manuell mit Tools und kommerzieller Software
nachgebessert. Für diese Arbeit wurde ein Algorithmus speziell für die auftretenden Fehler entwickelt, welches Löcher
in der Fläche sucht, indem es die Anzahl der unverbundenen Polygonkanten vergleicht. Sollte eine Polygonkante
keine Kante eines Nachbarpolygons aufweisen, wird dieses als Loch aus der Flächenrückführung erkannt.
Nachdem alle einfach vorhandenen Polygonkanten gefunden wurden, werden alle Kanten verbunden, die gleiche
Punktindices aufweisen. Die so verbundenen Kanten werden durch ein Polygon aus drei korrespondierenden Punkten
geschlossen. Dieser Schritt wird durchgeführt bis keine freien Kanten mehr detektiert werden und damit die
Löcher gefüllt sind.
Schließlich wird das geschlossene Volumenmodell als .stl und .vtk Datei exportiert. Sollte das Bauteil zuvor in mehrere
druckbare Unterteile aufgeteilt worden sein, werden nun für die restlichen Teile iterativ alle Prozessschritte
durchgeführt und die Bauteile im Anschluss von einem 3D Drucker eingelesen und gedruckt.
DVS 332 5