Mathcad - ee217projtodonew2.mcd
Mathcad - ee217projtodonew2.mcd
Mathcad - ee217projtodonew2.mcd
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
100<br />
10<br />
1<br />
0.1<br />
0.01<br />
0.01 0.1 1 10 100<br />
| S11 |<br />
| S21 |<br />
| S12 |<br />
| S22 |<br />
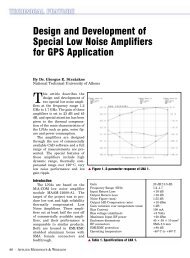
Fig. 8: S Parameters vs. Frequency<br />
Stability Analysis<br />
Often it happens a designer designs an amplifier, but he gets an oscillator in return. This<br />
scenario typically occurs at frequencies out of the desired band, where the source and load<br />
impedances can be unknown. If the out of band source and load impedances are unknown it is<br />
desirable to make the amplifier stable for all source and load impedances. This is known as an<br />
unconditionaly stable amplifier. If the out-of-band source and load impedances are known it is<br />
possible to design a conditionally stable amplifier design. Usually conditionally stable amplifiers<br />
can acheive higher performance levels than unconditionally stable amplifiers. This is becuase<br />
the amplifier performance must be degraded some with form of ballasting resistor to make it<br />
stable.<br />
It is desirable to make the stability factor greater than one for another reason other than<br />
stability. With a K factor greater than one it is possible to simultaneously conjugate match the<br />
input and output impedance of the amplifier. Conjugate matches are desirable, because the<br />
filters connected to the amplifier require a conjugate impedance to provide their specified<br />
frequency response.<br />
For a K factor of one, the real part of the matching impedances is zero ohms, so it is<br />
impossible to match with practical matching networks. For this same reason it is desirable to<br />
make the K factor some value significantly larger than one.<br />
KS ( ) ∆ S .<br />
1, 1<br />
S 22 ,<br />
S .<br />
12<br />
,<br />
S 2,<br />
1<br />
1 ( ∆ ) 2 2<br />
S 1, 1<br />
2. S .<br />
1,<br />
2<br />
S 21 ,<br />
2<br />
S 2, 2<br />
K Sparam N, I C , s = 1.016<br />
The mu factor is often a more desirable parameter to use for stability than K factor. This is<br />
because the K factor must be specified with other conditions, such as ∆. In this sense the µ<br />
factor is easier to use, because it does not require any other parameters to guarantee<br />
unconditional stability. Although the K factor and µ factor curves are different, their values are<br />
equal for the transition point between unconditionally stable and conditionally stable regions<br />
(K=µ=1). µ S<br />
.<br />
, , s = 1.102<br />
( ) ∆ S .<br />
1, 1<br />
S 22 ,<br />
S 12<br />
S 1 1<br />
,<br />
S 2,<br />
1<br />
2<br />
1 S 22 ,<br />
,<br />
∆ . S 2,<br />
2<br />
S .<br />
2 1<br />
,<br />
S 12 ,<br />
µ Sparam N I C