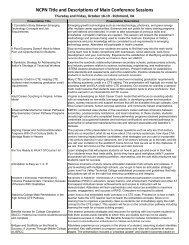
Chapter 10 - NCPN

More documents

Recommendations

Info

$hvvrq 6\vwhpv ri &rqlf 6hfwlrqv - NCPN$

30. A stretch of highway has a 12° angle of incline. What is this angle measure in radians ≠ 15 radians 31. Kimmy skated from point A to point B along the outside of the skating rink. How far did she travel Round your answer to the nearest foot. 314 ft 32. The temperature, in degrees Fahrenheit, inside a refrigerator can be modeled by the function y = 38 + 1.5cos ≠x , where x is the 10 number of minutes after the refrigerator’s motor begins to run. 448 Chapter 10 Trigonometric Functions and Identities a. The warmest temperature inside the refrigerator occurs just as the motor begins to run. What is this temperature 39.5ºF b. The motor runs for 10 minutes until the air inside the refrigerator is cooled to its lowest temperature. Then the motor rests for 10 minutes before it begins to run. What is the coolest temperature inside the refrigerator 36.5ºF 33. Nancy attaches a reflector to one of the spokes of her bicycle tire for increased visibility in low light. The position of the reflector relative to the ground as Nancy pedals down the street is given by the function h(x) = 10 + 7sin 4πx. In the function, x is the number of seconds since Nancy began pedaling, and h(x) is the height, in inches, of the reflector above the ground. a. How long does it take for the reflector to complete one full rotation Verify your answer by substituting it into the function. 0.5 s b. What is the maximum height of the reflector above the ground 17 in. Mixed Review State whether or not each infinite geometric series converges or diverges. Then determine whether or not each series has a sum. d ) ∑ . ( ) ∞ ∑ ( d= 1 ∞ 34. 5 1 2 35. 045 10 9 b= 1 converges; has a sum b diverges; does not have a sum 36. A radio tower is located 10 miles east and 15 miles north of the origin on a map of Reedsburg. The tower has enough power to broadcast over a radius of 40 miles. Write an equation to model the area of the broadcast of the radio tower. (x – 10) 2 + (y – 15) 2 = 40 2
Lesson 10.3 Inverse Trigonometric Functions Objectives Find the angle measure given the side lengths of a triangle. Joshua and his friends built a skateboarding ramp. The ramp is 5 feet long and 2 feet high. What is the angle of the ramp’s incline Evaluating Inverse Trigonometric Functions An inverse function is a mathematical function that “undoes” another function. That is, if f and f –1 are inverse functions, (f ◦ f –1 )(x) = x and (f –1 ◦ f )(x) = x. For the sin, cos, and tan functions, the corresponding inverse functions are sin –1 , cos –1 , and tan –1 . Example 1 Evaluating Inverse Trigonometric Functions Use a calculator to find the measure, in radians, of an angle that has a sine value of 0.707. Round your answer to the nearest hundredth. Solution Be sure the calculator is in RADIAN mode. Enter the sine value on the calculator. Then use the sin –1 function to evaluate the inverse trigonometric function. sin –1 (0.707) ≈ 0.79 radians Ongoing Assessment Use a calculator to find the measure, in degrees, of an angle that has a tangent value of 2.145. Round your answer to the nearest whole degree. Be sure the calculator is in DEGREE mode. 65° 10.3 Inverse Trigonometric Functions 449
Page 1 and 2: Chapter 10 Contents 10.1 Right Tria
Page 3 and 4: Lesson 10.1 Right Triangle Trigonom
Page 5 and 6: Solution Use the definitions of the
Page 7 and 8: Solve for x in each right triangle.
Page 9 and 10: 30. A wheelchair ramp is 20 feet lo
Page 11 and 12: Arc Length The unit circle has a ra
Page 13 and 14: Using a Calculator A scientific cal
Page 15: Find the length of the intercepted
Page 19 and 20: see margin After taking off, a comm
Page 21 and 22: 20. What is the angle of descent of
Page 23 and 24: The y-values on the unit circle are
Page 25 and 26: Example 2 Graphing Cosine Functions
Page 27 and 28: Activity Using a Graphing Calculato
Page 29 and 30: 25. The function y = 3sin ≠ t mod
Page 31 and 32: Ongoing Assessment In PQR, m∠P =
Page 33 and 34: Activity Ambiguous Cases Two triang
Page 35 and 36: Lesson Assessment Think and Discuss
Page 37 and 38: 23. Two points in a forest, A and B
Page 39 and 40: Lesson 10.6 Verifying Trigonometric
Page 41 and 42: Activity 2 Using the Pythagorean Id
Page 43 and 44: Lesson 10.7 Angle Sum and Differenc
Page 45 and 46: Practice and Problem Solving Use a
Page 47 and 48: Lesson 13.4 Double-Angle and Half-A
Page 49 and 50: When Trigonometric Function Values
Page 51 and 52: Practice and Problem Solving Use a
Page 53 and 54: Lesson 10.9 Solving Trigonometric E
Page 55 and 56: Use the Zero-Product Property to se
Page 57 and 58: Practice and Problem Solving Solve
Page 59 and 60: Math Labs Activity 1: The Circle of
Page 61 and 62: Activity 3: The Sine Curve of Biorh
Page 63 and 64: 3 Hold a protractor upside down so
Page 65 and 66: 3 Cale, Tammie, and Allison are mem
Page 67 and 68:
8 Bella does freelance marketing wo
Page 69 and 70:
Health Occupations 13 Dmitri wants
Page 71 and 72:
Lessons 10.5 and 10.6 Review Exampl
Page 73:
Standardized Test Practice Multiple
show all

Chapter 10 - NCPN

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?