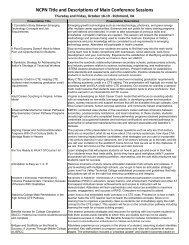
Chapter 10 - NCPN

Lesson 10.9 Solving Trigonometric
Equations
Objectives
Solve trigonometric
equations.
While trigonometric identities are true for all values of θ, most
trigonometric equations are true for only certain values of θ.
Trigonometric equations can be solved by collecting like terms,
finding square roots, factoring, and substitution.
Collecting Like Terms
Example 1 Solving by Collecting Like Terms
Solve 2cos θ – 1 + 3cos θ = cos θ for 0 ≤ θ < 2π.
Solution
Collect like terms to isolate cos θ on one side of the equation.
2cos θ – 1 + 3cos θ = cos θ
2cos θ – 1 + 1 + 3cos θ – cos θ = cos θ – cos θ + 1
4cos θ = 1
cos θ = 1 4
Use the inverse cosine function and a graphing calculator to solve
for θ.
cos –1 (cos θ) = cos –1 1 4
θ ≈ 1.32
Because the cosine function is also positive in the fourth quadrant,
2π – 1.32 ≈ 4.97 radians is also a solution to the trigonometric
equation. The two solutions for 0 ≤ θ ≤ 2π are 1.32 and 4.97 radians.
Ongoing Assessment
Solve 4tan θ – 3 = 2tan θ – 2 for 0 ≤ θ < 2π.
Finding Square Roots
Example 2 Solving by Square Roots
Solve 4sin 2 θ – 1 = 0 for 0 ≤ θ < 2π.
10.9 Solving Trigonometric Equations 485