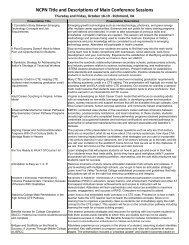
Chapter 10 - NCPN
Chapter 10 - NCPN
Chapter 10 - NCPN
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
Activity 2<br />
Using the Pythagorean Identity<br />
to Find Trigonometric Values<br />
Let cosθ = 4 and θ be in quadrant IV. Find sinθ and tanθ.<br />
5<br />
1 Complete the table using in the Pythagorean Identity.<br />
Step<br />
cos 2 θ + sin 2 θ = 1<br />
Reason<br />
Pythagorean Identity<br />
2<br />
⎛4⎞<br />
⎝⎜<br />
5⎠⎟ + sin2 θ = 1 Substitute 4 5<br />
for cos θ.<br />
16<br />
25 + sin2 θ = 1 Simplify the exponent.<br />
sin 2 θ = 9 25<br />
Subtract 16<br />
25<br />
from both sides.<br />
sin θ = 3 5<br />
Take the square root of both sides.<br />
2 Determine whether sine is positive or negative in quadrant IV.<br />
sin is negative in quadrant IV.<br />
3 Find sin θ in quadrant IV. sin θ = − 3 5<br />
4 Find tan θ in quadrant IV. Show your work. see margin<br />
Lesson Assessment<br />
Think and Discuss<br />
see margin<br />
1. Give an example of a trigonometric identity that is equal to 1.<br />
2. How can sin θ be expressed in terms of cos θ<br />
3. What does it mean for a trigonometric equation to be a<br />
trigonometric identity<br />
4. Which trigonometric function is the reciprocal of the<br />
sine function<br />
5. Create a trigonometric identity of your own by beginning with a<br />
simple trigonometric expression and working backward.<br />
<strong>10</strong>.6 Verifying Trigonometric Identities 473