a reduced model for internal waves interacting with submarine ...

0.5
0.4
0.3
0.2
η
0.1
0
−0.1
−0.2
−0.3
0 10 20 30 40 50 60
ξ
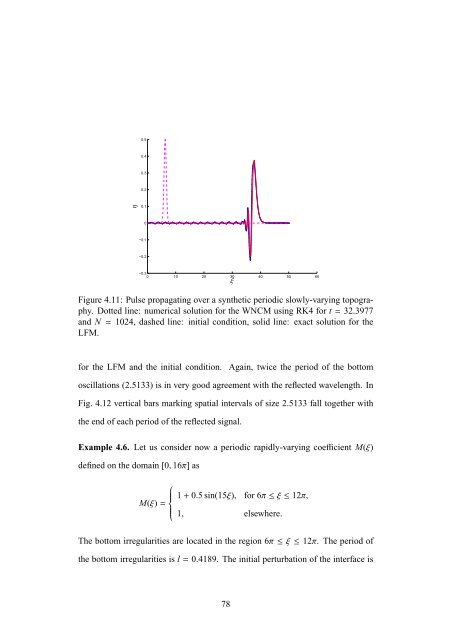
Figure 4.11: Pulse propagating over a synthetic periodic slowly-varying topography.
Dotted line: numerical solution for the WNCM using RK4 for t=32.3977
and N = 1024, dashed line: initial condition, solid line: exact solution for the
LFM.
for the LFM and the initial condition. Again, twice the period of the bottom
oscillations (2.5133) is in very good agreement with the reflected wavelength. In
Fig. 4.12 vertical bars marking spatial intervals of size 2.5133 fall together with
the end of each period of the reflected signal.
Example 4.6. Let us consider now a periodic rapidly-varying coefficient M(ξ)
defined on the domain [0, 16π] as
⎧
⎪⎨ 1+0.5 sin(15ξ), for 6π≤ξ≤12π,
M(ξ)=
⎪⎩ 1, elsewhere.
The bottom irregularities are located in the region 6π≤ξ≤12π. The period of
the bottom irregularities is l=0.4189. The initial perturbation of the interface is
78