anytime algorithms for learning anytime classifiers saher ... - Technion

Technion - Computer Science Department - Ph.D. Thesis PHD-2008-12 - 2008
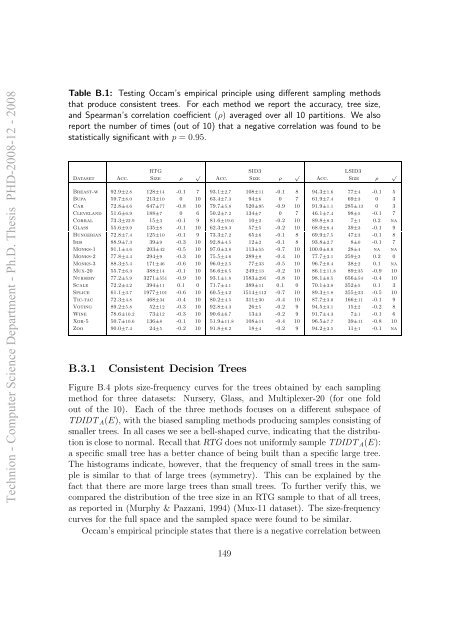
Table B.1: Testing Occam’s empirical principle using different sampling methods
that produce consistent trees. For each method we report the accuracy, tree size,
and Spearman’s correlation coefficient (ρ) averaged over all 10 partitions. We also
report the number of times (out of 10) that a negative correlation was found to be
statistically significant with p = 0.95.
RTG SID3 LSID3
√
√
Dataset Acc. Size ρ Acc. Size ρ Acc. Size ρ
Breast-w 92.9±2.8 128±14 -0.1 7 93.1±2.7 108±11 -0.1 8 94.3±1.6 77±4 -0.1 5
Bupa 59.7±8.0 213±10 0 10 63.4±7.3 94±6 0 7 61.9±7.4 69±3 0 3
Car 72.8±4.6 647±77 -0.8 10 79.7±5.8 520±95 -0.9 10 91.9±1.1 285±13 0 3
Cleveland 51.6±6.9 188±7 0 6 50.2±7.2 134±7 0 7 46.1±7.4 98±5 -0.1 7
Corral 73.3±22.9 15±3 -0.1 9 81.6±19.6 10±2 -0.2 10 89.8±8.3 7±1 0.2 na
Glass 55.6±9.9 135±8 -0.1 10 62.3±9.3 57±5 -0.2 10 68.0±8.4 39±3 -0.1 9
Hungerian 72.8±7.4 125±10 -0.1 9 73.3±7.2 65±6 -0.1 8 69.9±7.5 47±3 -0.1 8
Iris 88.9±7.3 39±9 -0.3 10 92.8±4.5 12±2 -0.1 8 93.8±2.7 8±0 -0.1 7
Monks-1 91.1±4.6 203±42 -0.5 10 97.0±3.8 113±55 -0.7 10 100.0±0.0 28±4 na na
Monks-2 77.8±4.4 294±9 -0.3 10 75.5±4.6 289±8 -0.4 10 77.7±3.1 259±3 0.2 0
Monks-3 88.3±5.4 171±46 -0.6 10 96.0±2.5 77±33 -0.5 10 96.7±0.4 38±2 0.1 na
Mux-20 55.7±6.3 388±14 -0.1 10 56.6±6.5 249±13 -0.2 10 86.1±11.8 89±35 -0.9 10
Nursery 77.2±5.9 3271±551 -0.9 10 93.1±1.8 1583±295 -0.8 10 98.1±0.5 656±54 -0.4 10
Scale 72.2±4.2 394±11 0.1 0 71.7±4.1 389±11 0.1 0 70.1±3.8 352±5 0.1 3
Splice 61.1±3.7 1977±101 -0.6 10 60.5±4.2 1514±112 -0.7 10 89.3±1.8 355±23 -0.5 10
Tic-tac 72.3±4.8 468±34 -0.4 10 80.2±4.5 311±30 -0.4 10 87.7±3.0 166±11 -0.1 9
Voting 89.2±5.8 52±12 -0.3 10 92.8±4.3 26±5 -0.2 9 94.5±3.1 15±2 -0.2 8
Wine 78.6±10.2 73±12 -0.3 10 90.6±6.7 13±3 -0.2 9 91.7±4.3 7±1 -0.1 6
Xor-5 50.7±10.6 136±8 -0.1 10 51.9±11.8 108±11 -0.4 10 96.5±7.7 39±11 -0.8 10
Zoo 90.0±7.4 24±5 -0.2 10 91.8±6.2 18±4 -0.2 9 94.2±3.5 11±1 -0.1 na
B.3.1 Consistent Decision Trees
Figure B.4 plots size-frequency curves for the trees obtained by each sampling
method for three datasets: Nursery, Glass, and Multiplexer-20 (for one fold
out of the 10). Each of the three methods focuses on a different subspace of
TDIDT A(E), with the biased sampling methods producing samples consisting of
smaller trees. In all cases we see a bell-shaped curve, indicating that the distribution
is close to normal. Recall that RTG does not uniformly sample TDIDT A(E):
a specific small tree has a better chance of being built than a specific large tree.
The histograms indicate, however, that the frequency of small trees in the sample
is similar to that of large trees (symmetry). This can be explained by the
fact that there are more large trees than small trees. To further verify this, we
compared the distribution of the tree size in an RTG sample to that of all trees,
as reported in (Murphy & Pazzani, 1994) (Mux-11 dataset). The size-frequency
curves for the full space and the sampled space were found to be similar.
Occam’s empirical principle states that there is a negative correlation between
149
√