Diffusion Processes with Hidden States from ... - FU Berlin, FB MI

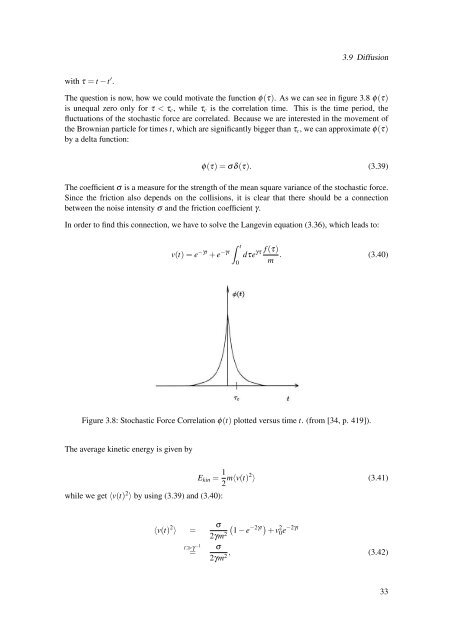
3.9 Diffusionwith τ = t −t ′ .The question is now, how we could motivate the function φ(τ). As we can see in figure 3.8 φ(τ)is unequal zero only for τ < τ c , while τ c is the correlation time. This is the time period, thefluctuations of the stochastic force are correlated. Because we are interested in the movement ofthe Brownian particle for times t, which are significantly bigger than τ c , we can approximate φ(τ)by a delta function:φ(τ) = σδ(τ). (3.39)The coefficient σ is a measure for the strength of the mean square variance of the stochastic force.Since the friction also depends on the collisions, it is clear that there should be a connectionbetween the noise intensity σ and the friction coefficient γ.In order to find this connection, we have to solve the Langevin equation (3.36), which leads to:v(t) = e −γt + e −γt ˆ t0γτ f (τ)dτem . (3.40)Figure 3.8: Stochastic Force Correlation φ(t) plotted versus time t. (from [34, p. 419]).The average kinetic energy is given bywhile we get 〈v(t) 2 〉 by using (3.39) and (3.40):E kin = 1 2 m〈v(t)2 〉 (3.41)〈v(t) 2 〉 =t≫γ −1=σ (1 − e−2γt )2γm 2 + v 2 0e −2γtσ2γm 2 , (3.42)33