analysis of water injection into high-temperature mixture of ...

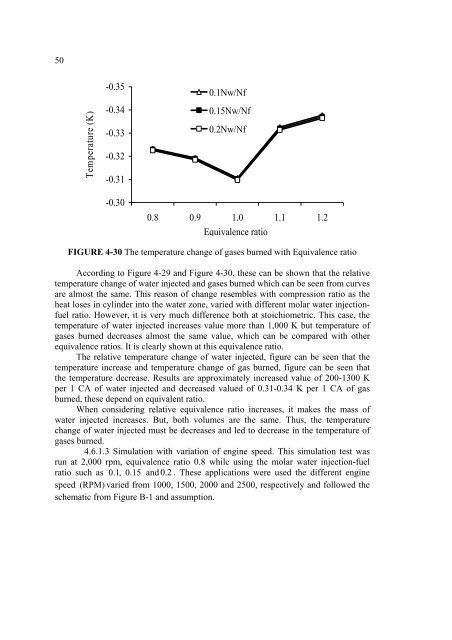
50Temperature (K)-0.35-0.34-0.33-0.32-0.31-0.300.1Nw/Nf0.15Nw/Nf0.2Nw/Nf0.8 0.9 1.0 1.1 1.2Equivalence ratioFIGURE 4-30 The temperature change of gases burned with Equivalence ratioAccording to Figure 4-29 and Figure 4-30, these can be shown that the relativetemperature change of water injected and gases burned which can be seen from curvesare almost the same. This reason of change resembles with compression ratio as theheat loses in cylinder into the water zone, varied with different molar water injectionfuelratio. However, it is very much difference both at stoichiometric. This case, thetemperature of water injected increases value more than 1,000 K but temperature ofgases burned decreases almost the same value, which can be compared with otherequivalence ratios. It is clearly shown at this equivalence ratio.The relative temperature change of water injected, figure can be seen that thetemperature increase and temperature change of gas burned, figure can be seen thatthe temperature decrease. Results are approximately increased value of 200-1300 Kper 1 CA of water injected and decreased valued of 0.31-0.34 K per 1 CA of gasburned, these depend on equivalent ratio.When considering relative equivalence ratio increases, it makes the mass ofwater injected increases. But, both volumes are the same. Thus, the temperaturechange of water injected must be decreases and led to decrease in the temperature ofgases burned.4.6.1.3 Simulation with variation of engine speed. This simulation test wasrun at 2,000 rpm, equivalence ratio 0.8 while using the molar water injection-fuelratio such as 0.1 , 0.15 and 0.2 . These applications were used the different enginespeed (RPM) varied from 1000, 1500, 2000 and 2500, respectively and followed theschematic from Figure B-1 and assumption.