Sweating the Small Stuff: Does data cleaning and testing ... - Frontiers

More documents

Recommendations

Info

Cummiskey et al.Testing assumptions with classroom datawe emphasize the influence a researcher’s judgment can have onstudy conclusions.Reforms in statistics education encourage an emphasis onunderstanding of concepts, interpretation, and data analysisinstead of formulas, computation, and mathematical theory(Garfield et al., 2007; DeVeaux and Velleman, 2008). Curriculabased on these reforms move away from teaching statisticsas a collection of facts. Instead, they encourage the scientificprocess of interdisciplinary data analysis as statistics is actuallypracticed. Paul Velleman states, “It seems that we have notmade [this] clear to others – and especially not to our students– that good statistical analyses include judgments, and wehave not taught our students how to make those judgments”(Velleman, 2008). Our classroom activities and correspondingdatasets demonstrate the importance of emphasizing these pointsand offer ideas for those teaching courses involving data analysisand experimental design to introduce the discussion in theclassroom.THE TANGRAMS GAME AND LABTangrams is an ancient Chinese puzzle where players arrangegeometrically shaped pieces into a particular design by flipping,rotating, and moving them. The online Tangrams game and theweb interface, shown in Figure 1, allow students the opportunityto play many versions of the original game.Prior to starting the game, the class decides upon one or moreresearch questions they want to investigate as a group. For example,students may decide to test whether the game completiontime depends on the type of music played in the background,or they could test if one gender is more likely to use hints. Studentsthen design the experiment by determining appropriategame settings and conditions for collecting the data. After thestudent researchers design the experiment, they become subjectsin the study by playing the game. The website collects the players’information and records their completion times. The data isavailable for immediate use through the website. If one researchstudy is designed for the entire class, every student plays the gameunder similar conditions and a large sample of data is immediatelyavailable through the website for analysis. The studentsreturn to their role of researcher using the data that they justcollected.Next, students (as a class or in small groups) make decisionsabout data cleaning, check assumptions, perform a statistical testof significance, and state their conclusions. Classroom testing ofthe Tangrams game and associated labs over the last three semestershas given us a rich data set demonstrating the impacts ofdata cleaning and the importance of validating the assumptionsof statistical tests.The Tangrams game-based lab gives students exposure to theentire research process: developing research questions, formulatinghypotheses,designing experiments,gathering data,performingstatistical tests, and arriving at appropriate conclusions. 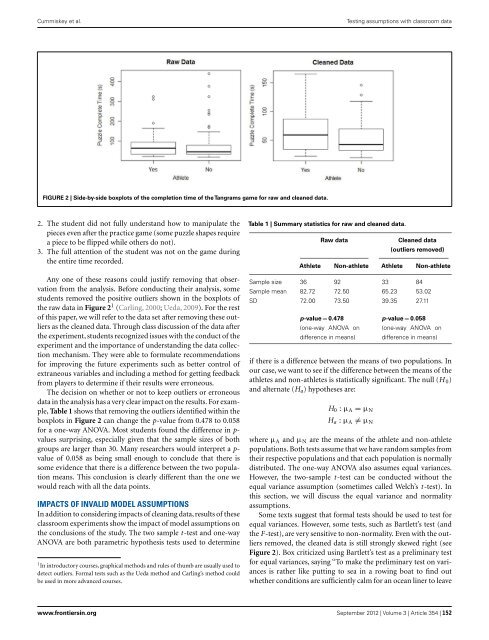This lab isa fun and effective way for instructors to transition from textbookproblems that focus on procedures to deeper learning experiencesthat emphasize the importance of proper experimental design andunderstanding assumptions.IMPACTS OF DATA CLEANINGFigure 2 shows boxplots of data collected at West Point in thefall semester of 2011 for one research question. The dependentvariable is the time to successfully complete a specified Tangramspuzzle. The independent variable is athlete (Yes means the studentplays on a collegiate team while No means the student does notplay on a collegiate team). Students were given an overview of thegame by their instructor and then allowed to practice the gameonce on a different puzzle in order to get familiar with the gamecontrols. For both groups, the distributions of completion timesappear unimodal with a large positive skew. There are several outlierspresent within the dataset. Discussing the data with studentstends to provide the following reasons for at least some of the veryhigh times:1. The student did not fully understand the object of the gameeven after the practice game.FIGURE 1 | Tangrams web interface.Frontiers in Psychology | Quantitative Psychology and Measurement September 2012 | Volume 3 | Article 354 | 151
Cummiskey et al.Testing assumptions with classroom dataFIGURE 2 | Side-by-side boxplots of the completion time of the Tangrams game for raw and cleaned data.2. The student did not fully understand how to manipulate thepieces even after the practice game (some puzzle shapes requirea piece to be flipped while others do not).3. The full attention of the student was not on the game duringthe entire time recorded.Any one of these reasons could justify removing that observationfrom the analysis. Before conducting their analysis, somestudents removed the positive outliers shown in the boxplots ofthe raw data in Figure 2 1 (Carling, 2000; Ueda, 2009). For the restof this paper, we will refer to the data set after removing these outliersas the cleaned data. Through class discussion of the data afterthe experiment, students recognized issues with the conduct of theexperiment and the importance of understanding the data collectionmechanism. They were able to formulate recommendationsfor improving the future experiments such as better control ofextraneous variables and including a method for getting feedbackfrom players to determine if their results were erroneous.The decision on whether or not to keep outliers or erroneousdata in the analysis has a very clear impact on the results. For example,Table 1 shows that removing the outliers identified within theboxplots in Figure 2 can change the p-value from 0.478 to 0.058for a one-way ANOVA. Most students found the difference in p-values surprising, especially given that the sample sizes of bothgroups are larger than 30. Many researchers would interpret a p-value of 0.058 as being small enough to conclude that there issome evidence that there is a difference between the two populationmeans. This conclusion is clearly different than the one wewould reach with all the data points.IMPACTS OF INVALID MODEL ASSUMPTIONSIn addition to considering impacts of cleaning data, results of theseclassroom experiments show the impact of model assumptions onthe conclusions of the study. The two sample t -test and one-wayANOVA are both parametric hypothesis tests used to determine1 In introductory courses, graphical methods and rules of thumb are usually used todetect outliers. Formal tests such as the Ueda method and Carling’s method couldbe used in more advanced courses.Table 1 | Summary statistics for raw and cleaned data.Raw dataCleaned data(outliers removed)Athlete Non-athlete Athlete Non-athleteSample size 36 92 33 84Sample mean 82.72 72.50 65.23 53.02SD 72.00 73.50 39.35 27.11p-value = 0.478(one-way ANOVA ondifference in means)p-value = 0.058(one-way ANOVA ondifference in means)if there is a difference between the means of two populations. Inour case, we want to see if the difference between the means of theathletes and non-athletes is statistically significant. The null (H 0 )and alternate (H a ) hypotheses are:H 0 : µ A = µ NH a : µ A ̸= µ Nwhere µ A and µ N are the means of the athlete and non-athletepopulations. Both tests assume that we have random samples fromtheir respective populations and that each population is normallydistributed. The one-way ANOVA also assumes equal variances.However, the two-sample t -test can be conducted without theequal variance assumption (sometimes called Welch’s t -test). Inthis section, we will discuss the equal variance and normalityassumptions.Some texts suggest that formal tests should be used to test forequal variances. However, some tests, such as Bartlett’s test (andthe F-test), are very sensitive to non-normality. Even with the outliersremoved, the cleaned data is still strongly skewed right (seeFigure 2). Box criticized using Bartlett’s test as a preliminary testfor equal variances, saying “To make the preliminary test on variancesis rather like putting to sea in a rowing boat to find outwhether conditions are sufficiently calm for an ocean liner to leavewww.frontiersin.org September 2012 | Volume 3 | Article 354 | 152
Page 2 and 3:
FRONTIERS COPYRIGHTSTATEMENT© Copy
Page 4 and 5:
Table of Contents05 Is Data Cleanin
Page 7 and 8:
OsborneAssumptions and data cleanin
Page 9 and 10:
ORIGINAL RESEARCH ARTICLEpublished:
Page 12 and 13:
Hoekstra et al.Why assumptions are
Page 14 and 15:
Page 16 and 17:
Page 18 and 19:
Page 20 and 21:
García-PérezStatistical conclusio
Page 22 and 23:
Page 24 and 25:
Page 26 and 27:
Page 28 and 29:
Page 30 and 31:
Sheng and ShengEffect of non-normal
Page 32 and 33:
Page 34 and 35:
Page 36 and 37:
Page 38 and 39:
Page 40 and 41:
Page 42 and 43:
REVIEW ARTICLEpublished: 12 April 2
Page 44 and 45:
Nimon et al.The assumption of relia
Page 46 and 47:
Page 48 and 49:
Page 50 and 51:
Page 52 and 53:
Page 54 and 55:
Page 56 and 57:
TressoldiPower replication unreliab
Page 58 and 59:
TressoldiPower replication unreliab
Page 60 and 61:
Page 62 and 63:
FinchModern methods for the detecti
Page 64 and 65:
Page 66 and 67:
Page 68 and 69:
Page 70 and 71:
Page 72 and 73:
MINI REVIEW ARTICLEpublished: 28 Au
Page 74 and 75:
NimonStatistical assumptionsand Del
Page 76 and 77:
NimonStatistical assumptionsFor exa
Page 78 and 79:
Kraha et al.Interpreting multiple r
Page 80 and 81:
Page 82 and 83:
Page 84 and 85:
Page 86 and 87:
Page 88 and 89:
Page 90 and 91:
Page 92 and 93:
Page 94 and 95:
SmithsonComparing moderation of slo
Page 96 and 97:
Page 98 and 99:
Page 100 and 101:
Page 102 and 103: REVIEW ARTICLEpublished: 01 March 2
Page 104 and 105: Flora et al.Factor analysis assumpt
Page 124 and 125: Kasper and ÜnlüAssumptions of fac
Page 144 and 145: Lages and JaworskaHow predictable a
Page 154 and 155: Cummiskey et al.Testing assumptions
Page 156 and 157: Cummiskey et al.Testing assumptions
Page 158: Cummiskey et al.Testing assumptions
show all

Sweating the Small Stuff: Does data cleaning and testing ... - Frontiers

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?