Noise generated by cavitating single-hole and multi-hole orifices in ...

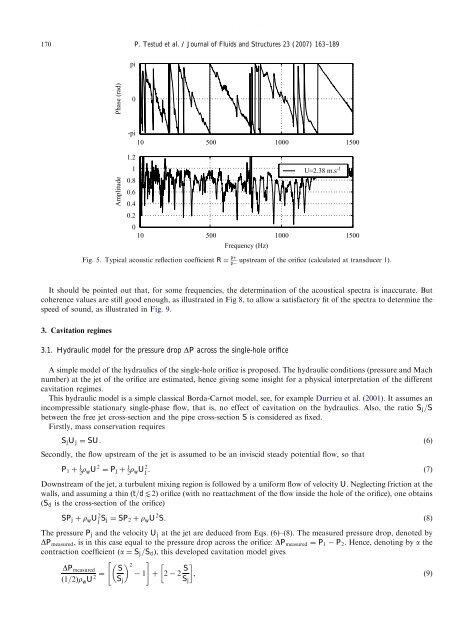
ARTICLE IN PRESS170P. Testud et al. / Journal of Fluids and Structures 23 (2007) 163–189piPhase (rad)0-pi10 500 1000 1500Amplitude1.21U=2.38 m.s -10.80.60.40.2010 500 1000 1500Frequency (Hz)Fig. 5. Typical acoustic reflection coefficient R ¼ pþpupstream of the orifice (calculated at transducer 1).It should be pointed out that, for some frequencies, the determination of the acoustical spectra is inaccurate. Butcoherence values are still good enough, as illustrated in Fig 8, to allow a satisfactory fit of the spectra to determine thespeed of sound, as illustrated in Fig. 9.3. Cavitation regimes3.1. Hydraulic model for the pressure drop DP across the single-hole orificeA simple model of the hydraulics of the single-hole orifice is proposed. The hydraulic conditions (pressure and Machnumber) at the jet of the orifice are estimated, hence giving some insight for a physical interpretation of the differentcavitation regimes.This hydraulic model is a simple classical Borda-Carnot model, see, for example Durrieu et al. (2001). It assumes anincompressible stationary single-phase flow, that is, no effect of cavitation on the hydraulics. Also, the ratio S j =Sbetween the free jet cross-section and the pipe cross-section S is considered as fixed.Firstly, mass conservation requiresS j U j ¼ SU. (6)Secondly, the flow upstream of the jet is assumed to be an inviscid steady potential flow, so thatP 1 þ 1 2 r wU 2 ¼ P j þ 1 2 r wU 2 j . (7)Downstream of the jet, a turbulent mixing region is followed by a uniform flow of velocity U. Neglecting friction at thewalls, and assuming a thin ðt=dt2Þ orifice (with no reattachment of the flow inside the hole of the orifice), one obtains(S d is the cross-section of the orifice)SP j þ r w U 2 j S j ¼ SP 2 þ r w U 2 S. (8)The pressure P j and the velocity U j at the jet are deduced from Eqs. (6)–(8). The measured pressure drop, denoted byDP measured , is in this case equal to the pressure drop across the orifice: DP measured ¼ P 1 P 2 . Hence, denoting by a thecontraction coefficient ða ¼ S j =S d Þ, this developed cavitation model gives" #DP measuredð1=2Þr w U 2 ¼ S 2 1 þ 2 2 S , (9)S jS j