MYSTERIES OF THE EQUILATERAL TRIANGLE - HIKARI Ltd

74 Mathematical Properties
in column m + 1 of row n + 1 of Pascal’s triangle. A regular n-simplex may
be constructed from a regular (n − 1)-simplex by connecting a new vertex to
all of the original vertices by an edge of length d. A regular n-simplex is so
named because it is the simplest regular polytope in n dimensions.
(a) (b)
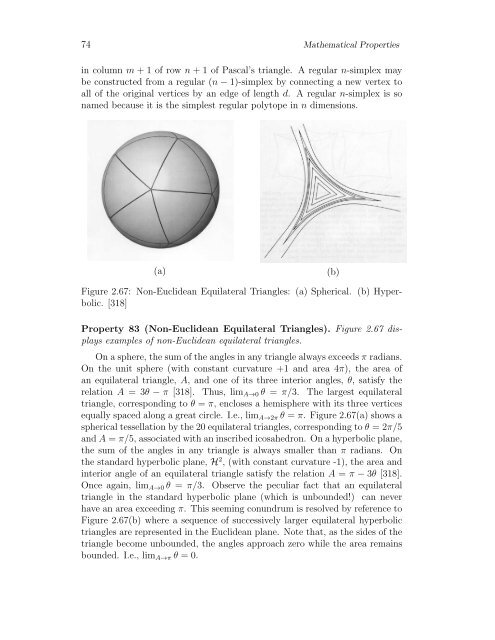
Figure 2.67: Non-Euclidean Equilateral Triangles: (a) Spherical. (b) Hyperbolic.
[318]
Property 83 (Non-Euclidean Equilateral Triangles). Figure 2.67 displays
examples of non-Euclidean equilateral triangles.
On a sphere, the sum of the angles in any triangle always exceeds π radians.
On the unit sphere (with constant curvature +1 and area 4π), the area of
an equilateral triangle, A, and one of its three interior angles, θ, satisfy the
relation A = 3θ − π [318]. Thus, limA→0 θ = π/3. The largest equilateral
triangle, corresponding to θ = π, encloses a hemisphere with its three vertices
equally spaced along a great circle. I.e., limA→2π θ = π. Figure 2.67(a) shows a
spherical tessellation by the 20 equilateral triangles, corresponding to θ = 2π/5
and A = π/5, associated with an inscribed icosahedron. On a hyperbolic plane,
the sum of the angles in any triangle is always smaller than π radians. On
the standard hyperbolic plane, H 2 , (with constant curvature -1), the area and
interior angle of an equilateral triangle satisfy the relation A = π − 3θ [318].
Once again, limA→0 θ = π/3. Observe the peculiar fact that an equilateral
triangle in the standard hyperbolic plane (which is unbounded!) can never
have an area exceeding π. This seeming conundrum is resolved by reference to
Figure 2.67(b) where a sequence of successively larger equilateral hyperbolic
triangles are represented in the Euclidean plane. Note that, as the sides of the
triangle become unbounded, the angles approach zero while the area remains
bounded. I.e., limA→π θ = 0.