Etude de la dynamique autour des points de Lagrange

tel-00422422, version 1 - 6 Oct 2009
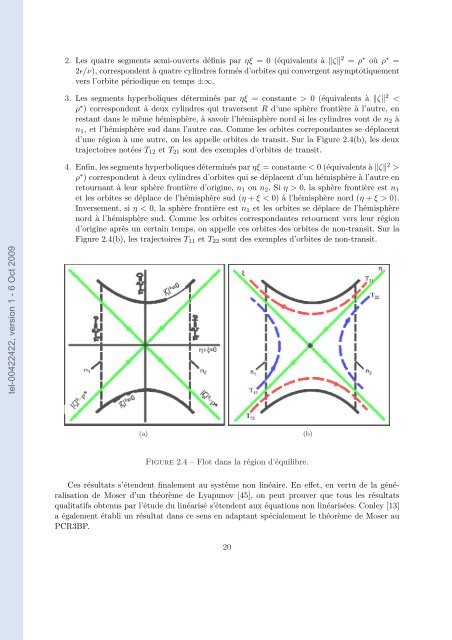
2. Les quatre segments semi-ouverts définis par ηξ = 0 (équivalents à ζ 2 = ρ ∗ où ρ ∗ =
2ɛ/ν), correspondent à quatre cylindres formés d’orbites qui convergent asymptotiquement
vers l’orbite périodique en temps ±∞.
3. Les segments hyperboliques déterminés par ηξ = constante > 0 (équivalents à ζ 2 <
ρ ∗ ) correspondent à deux cylindres qui traversent R d’une sphère frontière à l’autre, en
restant dans le même hémisphère, à savoir l’hémisphère nord si les cylindres vont de n2 à
n1, et l’hémisphère sud dans l’autre cas. Comme les orbites correpondantes se déplacent
d’une région à une autre, on les appelle orbites de transit. Sur la Figure 2.4(b), les deux
trajectoires notées T12 et T21 sont des exemples d’orbites de transit.
4. Enfin, les segments hyperboliques déterminés par ηξ = constante < 0 (équivalents à ζ 2 >
ρ ∗ ) correspondent à deux cylindres d’orbites qui se déplacent d’un hémisphère à l’autre en
retournant à leur sphère frontière d’origine, n1 ou n2. Si η > 0, la sphère frontière est n1
et les orbites se déplace de l’hémisphère sud (η + ξ < 0) à l’hémisphère nord (η + ξ > 0).
Inversement, si η < 0, la sphère frontière est n1 et les orbites se déplace de l’hémisphère
nord à l’hémisphère sud. Comme les orbites correspondantes retournent vers leur région
d’origine après un certain temps, on appelle ces orbites des orbites de non-transit. Sur la
Figure 2.4(b), les trajectoires T11 et T22 sont des exemples d’orbites de non-transit.
(a) (b)
Figure 2.4 – Flot dans la région d’équilibre.
Ces résultats s’étendent finalement au système non linéaire. En effet, en vertu de la généralisation
de Moser d’un théorème de Lyapunov [45], on peut prouver que tous les résultats
qualitatifs obtenus par l’étude du linéarisé s’étendent aux équations non linéarisées. Conley [13]
a également établi un résultat dans ce sens en adaptant spécialement le théorème de Moser au
PCR3BP.
20