2. Transformationer, Matriser och Operationer.
2. Transformationer, Matriser och Operationer.
2. Transformationer, Matriser och Operationer.
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
26 Nils Elander, 08/5537 8656 - 08/96 70 21 – 2003:1:26<br />
• Det ∃ en trivial lösning om det Ā = 0<br />
x = Ā −1 c = 0 (<strong>2.</strong>4.2)<br />
Bortse fr˚an den triviala lösningen !. Betrakta nu en vektor<br />
x = (x1, x2, · · · , xn) = x1ˆx1 + x2ˆx2 + · · · xnˆxn<br />
(<strong>2.</strong>4.3)<br />
Ekv.(<strong>2.</strong>4.1 <strong>och</strong> <strong>2.</strong>4.2) innebär att x är ortogonal mot vektorerna ai i ekv.(<strong>2.</strong>4.4) d˚a<br />
ortogonalitet innebär att skalärprodukten är lika med noll :<br />
d˚a<br />
ai = (Ai1, Ai2, · · · , Ain) (<strong>2.</strong>4.4)<br />
x · ai = (x1Ai1)(ˆx1 · ˆx1) + (x2Ai2)(ˆx2 · ˆx2) + · · · + (xnAin)(ˆxn · ˆxn) = 0 (<strong>2.</strong>4.5)<br />
Men ekv.(<strong>2.</strong>4.5) är det samma som<br />
d.v.s samma som de ekv. som bygger upp (<strong>2.</strong>4.1).<br />
x1Ai1 + x2Ai2 + · · · + xnAin = 0 (<strong>2.</strong>4.6)<br />
Betrakta nu en tredimensionell matris. Ā <strong>och</strong> ett egenvärdesproblem<br />
Āx = 0 ⇐⇒ ai · x = 0 ⇐⇒ x ⊥ ai i = 1, 2, 3. (<strong>2.</strong>4.7)<br />
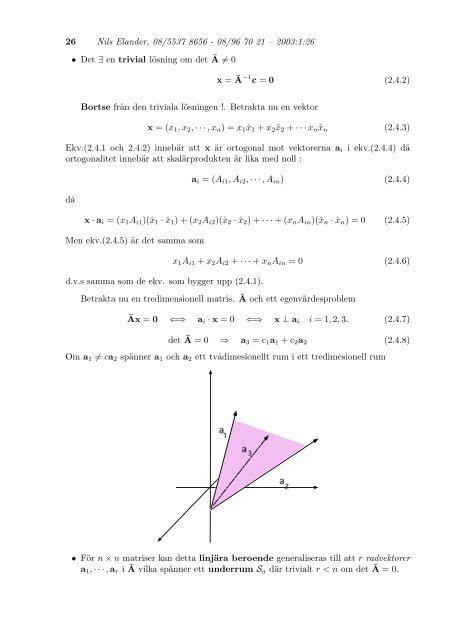
det Ā = 0 ⇒ a3 = c1a1 + c2a2 (<strong>2.</strong>4.8)<br />
Om a1 = ca2 spänner a1 <strong>och</strong> a2 ett tv˚adimesionellt rum i ett tredimesionell rum<br />
• För n × n matriser kan detta linjära beroende generaliseras till att r radvektorer<br />
a1, · · · , ar i Ā vilka spänner ett underrum Sa där trivialt r < n om det Ā = 0.






![Final Examination Paper for Electrodynamics-I [Solutions]](https://img.yumpu.com/21085948/1/184x260/final-examination-paper-for-electrodynamics-i-solutions.jpg?quality=85)








