5.1 INTEGRALES DOBLES 5.2 INTEGRALES TRIPLES
5.1 INTEGRALES DOBLES 5.2 INTEGRALES TRIPLES
5.1 INTEGRALES DOBLES 5.2 INTEGRALES TRIPLES
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
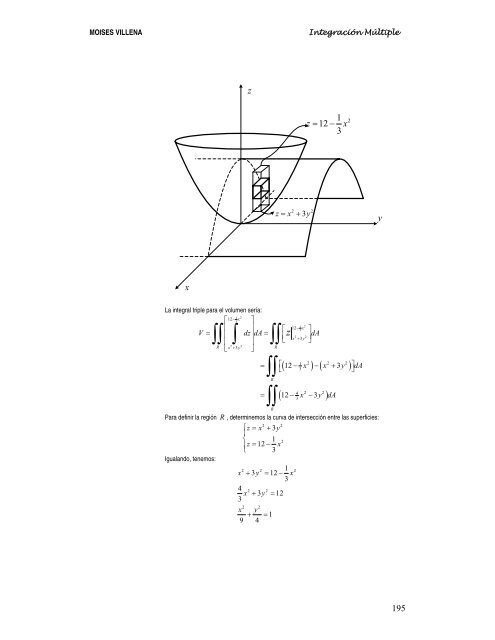
MOISES VILLENA Integración Múltiple<br />
x<br />
La integral triple para el volumen sería:<br />
1 2<br />
⎡12− x<br />
3 ⎤<br />
1 2<br />
⎢ ⎥ ⎡ 12−<br />
x 3 ⎤<br />
V = ⎢ dz⎥dA= z dA<br />
2 2<br />
x + 3 y ∫∫ ⎢ ⎥<br />
⎢∫⎥ ∫∫ ⎣ ⎦<br />
R 2 2<br />
x + 3 y<br />
R<br />
⎣ ⎦<br />
z<br />
∫∫ R<br />
∫∫<br />
R<br />
z = x + 3y<br />
2 2<br />
1<br />
z = 12 − x<br />
3<br />
1 2 2 2<br />
( 12 3 ) ( 3 )<br />
= ⎡ x x y ⎤<br />
⎣<br />
− − +<br />
⎦<br />
dA<br />
4 2 2<br />
( 12 3 3 )<br />
= − x − y dA<br />
Para definir la región R , determinemos la curva de intersección entre las superficies:<br />
2 2<br />
⎧ z = x + 3y<br />
⎪<br />
⎨ 1 2<br />
⎪z<br />
= 12 − x<br />
⎩ 3<br />
Igualando, tenemos:<br />
2 2 1 2<br />
x + 3y = 12− x<br />
3<br />
4 2 2<br />
x + 3y = 12<br />
3<br />
2 2<br />
x y<br />
+ = 1<br />
9 4<br />
2<br />
y<br />
195