Diferenciální geometrie

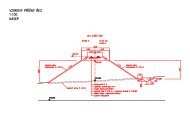
1.6. Frenetovy vzorce, křivosti 12Obrázek 1.5: Tečna t, hlavní normála n, binormála b, oskulační rovina τ,normálová rovina ν, rektifikační rovina µ křivky k v bodě XOznačme t(s 0 ) = ṖP (s 0 ) a n(s 0 ) = ¨P (s 0 )| ¨P (s 0 )| = 11 k · ¨P (s 0 ) = 11 k ·ṫt(s 0 ) jednotkovévektory tečny a hlavní normály. Dále b(s 0 ) = t(s 0 ) × n(s 0 ) je jednotkovývektor binormály. Ze vztahu b(s 0 )·b(s 0 ) = 1 plyne derivováním b(s 0 )·ḃb(s 0 ) =0. Tedy ḃb patří do zaměření oskulační roviny, tj. ḃb = At + Bn. Dále b · t = 0a derivováním ḃb · t + b ·ṫt = 0 ⇒ ḃb · t + b ·1 k · n = 0 ⇒ ḃb · t = 0. Jestliže rovniciḃb = At + Bn vynásobíme t, máme ḃb · t = A, ale to je nula. Tím jsme ukázali,že koeficient A je nulový a tedy vektory ḃb a n jsou kolineární. To nám dovolídefinovat druhou křivost křivky.Definice 8. Druhou křivostí křivky (torzí) v bodě rozumíme čísloneboli | 2 k(s 0 )| = |ḃb|.2 k(s 0 ) = −ḃb · n ,Věta 7. (Frenetovy vzorce) Pro regulární křivku parametrizovanou obloukemplatíṫt = 1 knṅn = − 1 kt + 2 kbḃb = − 2 kn .Důkaz. Máme tyto vztahyṫt = 1 knḃb = − 2 kn