Infoplaner 1-2007 - Cadfem

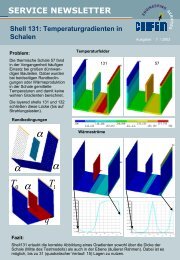
CADFEM INFOPLANER 1/2007Current Methods for the NumericalSimulation of Turbulent Flows44IntroductionTurbulent flows are highly unsteady flows, where the mainvelocity field is superimposed by random velocity fluctuations.In typical engineering applications, for instance, the flow pasta submarine as depicted in Figure 1, turbulent flows are prevalent,among other things, due to their positive features such asa more effective transport and mixing ability with respect to acomparable laminar flow. As a result, the general interest in theturbulent state of flow is very high. This brief accomodates thatinterest by focusing on the numerical simulation of turbulentflows, which requires to numerically solve the Navier-Stokesequations. This set of equations represents the mathematicalbasis for both states of flow, laminar and turbulent flow, althoughthese two states of flow are physically very different.The occurence of one or the other state strongly depends onthe Reynolds number associated with the flow. This articlemerely provides an overview on current approaches, with somereferences for further reading given at the end. For a descriptionof turbulent flows in general, the reader is particularly referredto [7] and [4].Currently, there are three basic conceptual alternatives for thenumerical simulation of turbulence:• Direct Numerical Simulation (DNS),• Large Eddy Simulation (LES), and• simulations based on the Reynolds Averaged Navier-Stokes(RANS) equations,ordered here according to the required computational effort.Figure 2 depicts the respective methods in front of the wellknownKolmogorov energy spectrum. The spectrum shows thedistribution of the energy among the various scales of a turbulentflow in wavenumber space (i.e., large scales represented bysmall wavenumbers and small scales by large wavenumbers).Most of the energy is intially contained in the large scales ofthe energy-containing range, which is then transferred in a cascade-likeprocess via the inertial subrange to the scales of thedissipation range, where the energy is eventually dissipated.The major problem making turbulent flow simulations difficultis the broad range of length and time scales appearing in aturbulent flow. A widely used assessment quantifying the ratioof the largest flow scale, L, and the smallest flow scale, the“Kolmogorov scale” , is given as, (1)assuming it proportional to the Reynolds number based on L.The methods will be briefly described in the following three sections,starting with RANS, which still has to be considered the“workhorse” for turbulence simulation, particularly in industrialapplications. Finally, two new approaches will be addressed:DES (i.e., a hybridbetween RANS andLES) and VMLES (i.e., anew approach to LES).The “Workhorse”:RANSThe RANS system ofequations is obtainedby Reynolds averagingof the Navier-Stokes equations. As a result of the averagingprocess, a closure problem arises, producing six additionalunknowns due to a (symmetric) Reynolds stress tensor, withoutadditional equations for those unknowns. Thus, a modelingapproach becomes necessary. The drawback compared to LES(see below) refers to the fact that the complete fluctuationsor, more precisely, the complete Reynolds stress tensor have tobe modeled. Turbulence models have to be used for this purposewhich are, however, lacking generality, since they haveto model an extremely wide range of scales, see Figure 2. Reynoldsstress models may be used, where transport equationsfor the unknown Reynolds stress tensor components and forthe dissipation (i.e., 7 additional differential equations) haveto be solved. Usually less accurate but substantially more efficientare turbulent viscosity models, which range fromFigure 1: Turbulent flow past asubmarine (source: Wikipedia).• zero-equation (or Algebraic) models such as the mixinglengthmodel over• one-equation models such as the Spalart-Allmaras model to• two-equation models such as the k − model.For an exhaustive description of RANS, the reader is referredto [8].Direct Numerical Simulation (DNS)A DNS is the theoretically most straightforward concept for thenumerical simulation of turbulent flows. It “merely” attempts tosolve the Navier-Stokes equations numerically (i.e., without anyadditional modeling efforts). A DNS aims at a complete resolutionof all scales contained in the respective flow. Hence, nounresolved scales would be left theoretically. The problem liesin the aforementioned broad range of length and time scalesappearing in a turbulent flow, which makes a DNS unfeasiblein most of the cases. Assuming (1) in all spatial directions, andconsidering the tightly linked temporal resolution, the numberof degrees of freedom in the simulation scales with Re 3 L . As aresult, a DNS still is not a viable method for simulating highor, for the most part, even moderately high Reynolds numberflows of engineering interest with the currently available computerhardware. For more information on DNS, the reader isreferred to [3] and [1].Basics