Progressively Interactive Evolutionary Multi-Objective Optimization ...

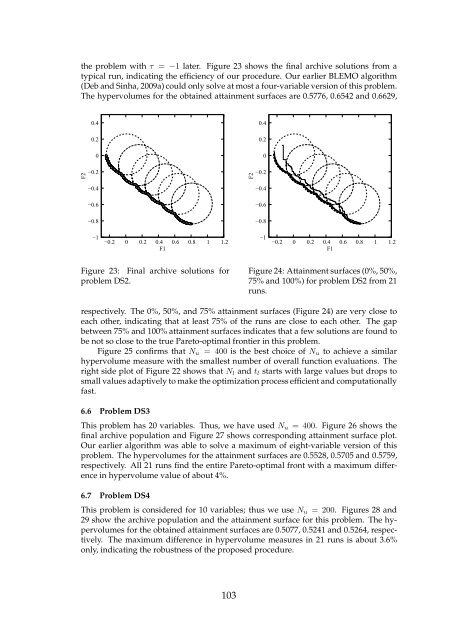
the problem with τ = −1 later. Figure 23 shows the final archive solutions from a
typical run, indicating the efficiency of our procedure. Our earlier BLEMO algorithm
(DebandSinha,2009a)couldonlysolveatmostafour-variableversionofthisproblem.
The hypervolumes for the obtained attainment surfaces are 0.5776, 0.6542 and 0.6629,
F2
0.4
0.2
0
−0.2
−0.4
−0.6
−0.8
−1
−0.2 0 0.2 0.4
F1
0.6 0.8 1 1.2
Figure 23: Final archive solutions for
problemDS2.
F2
0.4
0.2
0
−0.2
−0.4
−0.6
−0.8
−1
−0.2 0 0.2 0.4
F1
0.6 0.8 1 1.2
Figure24: Attainmentsurfaces(0%,50%,
75%and 100%)for problemDS2 from21
runs.
respectively. The 0%, 50%, and 75% attainment surfaces (Figure 24) are very close to
each other, indicating that at least 75% of the runs are close to each other. The gap
between75% and 100%attainment surfacesindicates that a few solutions arefound to
benot soclose tothe true Pareto-optimalfrontierinthis problem.
Figure 25 confirms that Nu = 400 is the best choice of Nu to achieve a similar
hypervolume measure with the smallest number of overall function evaluations. The
right side plot of Figure 22 shows that Nl and tl starts with large values but drops to
smallvaluesadaptivelytomaketheoptimizationprocessefficientandcomputationally
fast.
6.6 ProblemDS3
This problem has 20 variables. Thus, we have used Nu = 400. Figure 26 shows the
final archive population and Figure 27 shows corresponding attainment surface plot.
Our earlier algorithm was able to solve a maximum of eight-variable version of this
problem. The hypervolumes for the attainment surfaces are 0.5528, 0.5705and 0.5759,
respectively. All 21 runs find the entire Pareto-optimal front with a maximum differencein
hypervolume valueof about4%.
6.7 ProblemDS4
This problem is considered for 10 variables; thus we use Nu = 200. Figures 28 and
29 show the archive population and the attainment surface for this problem. The hypervolumes
for the obtained attainment surfaces are 0.5077,0.5241and 0.5264,respectively.
The maximum difference in hypervolume measures in 21 runs is about 3.6%
only, indicating the robustness of the proposedprocedure.
103