Progressively Interactive Evolutionary Multi-Objective Optimization ...

f2
D
C
Region
Dominated by A
B
A
Region
Dominating A
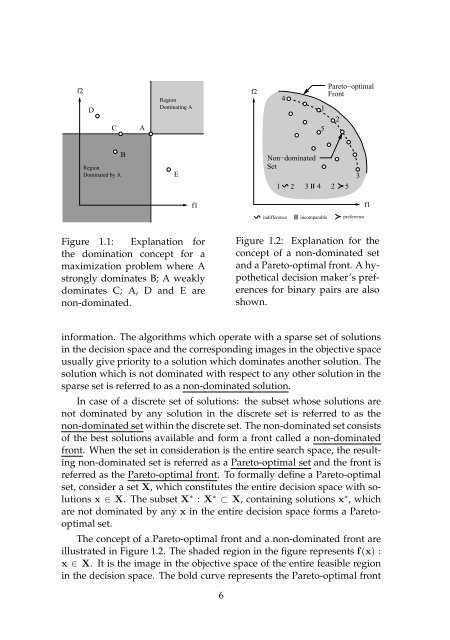
Figure 1.1: Explanation for
the domination concept for a
maximization problem where A
strongly dominates B; A weakly
dominates C; A, D and E are
non-dominated.
E
f1
f2
4
Non−dominated
Set
1 2 3 4 2 5
Pareto−optimal
Front
indifference incomparable preference
Figure 1.2: Explanation for the
concept of a non-dominated set
and a Pareto-optimal front. A hypothetical
decision maker’s preferences
for binary pairs are also
shown.
information. The algorithms which operate with a sparse set of solutions
in the decision space and the corresponding images in the objective space
usually give priority to a solution which dominates another solution. The
solution which is not dominated with respect to any other solution in the
sparse set is referred to as a non-dominated solution.
In case of a discrete set of solutions: the subset whose solutions are
not dominated by any solution in the discrete set is referred to as the
non-dominated set within the discrete set. The non-dominated set consists
of the best solutions available and form a front called a non-dominated
front. When the set in consideration is the entire search space, the resulting
non-dominated set is referred as a Pareto-optimal set and the front is
referred as the Pareto-optimal front. To formally define a Pareto-optimal
set, consider a set X, which constitutes the entire decision space with solutions
x ∈ X. The subset X ∗ : X ∗ ⊂ X, containing solutions x ∗ , which
are not dominated by any x in the entire decision space forms a Paretooptimal
set.
The concept of a Pareto-optimal front and a non-dominated front are
illustrated in Figure 1.2. The shaded region in the figure represents f(x) :
x ∈ X. It is the image in the objective space of the entire feasible region
in the decision space. The bold curve represents the Pareto-optimal front
6
1
5
2
3
f1