Projects - Cengage Learning

Appendix C C-15
and
http://www.svobodat.com/primes
An advantage to the latter site is that a list of primes is available in spreadsheet
format, in which it’s immediately clear which is the nth prime.
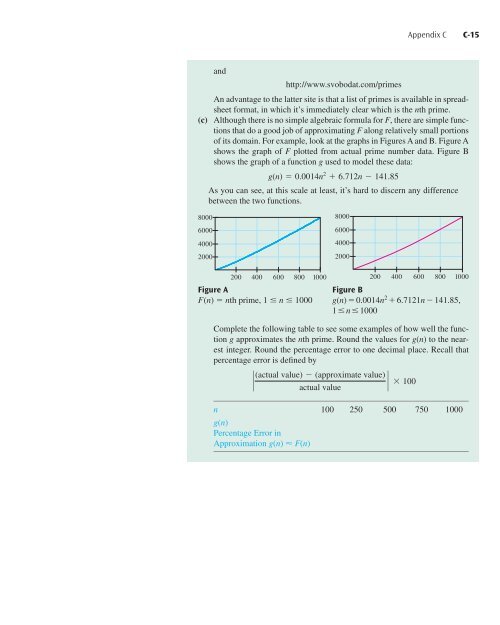
(c) Although there is no simple algebraic formula for F, there are simple functions
that do a good job of approximating F along relatively small portions
of its domain. For example, look at the graphs in Figures A and B. Figure A
shows the graph of F plotted from actual prime number data. Figure B
shows the graph of a function g used to model these data:
g(n) 0.0014n 2 6.712n 141.85
As you can see, at this scale at least, it’s hard to discern any difference
between the two functions.
8000
6000
4000
2000
8000
6000
4000
2000
200 400 600 800 1000
200 400 600 800 1000
Figure A
Figure B
F(n) nth prime, 1 n 1000 g(n)0.0014n 2 6.7121n 141.85,
1 n 1000
Complete the following table to see some examples of how well the function
g approximates the nth prime. Round the values for g(n) to the nearest
integer. Round the percentage error to one decimal place. Recall that
percentage error is defined by
(actual value) (approximate value)
`
` 100
actual value
n 100 250 500 750 1000
g(n)
Percentage Error in
Approximation g(n) F(n)