Student Seminar: Classical and Quantum Integrable Systems

Upper−half plane
01 01 0 0 1 1 01
−1/k
−1
1
1/k
sn x
K−i K’
K+i K’
+
−K
K
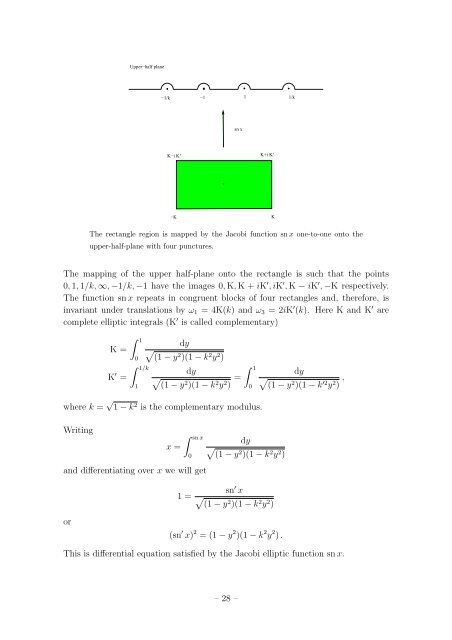
The rectangle region is mapped by the Jacobi function sn x one-to-one onto the
upper-half-plane with four punctures.
The mapping of the upper half-plane onto the rectangle is such that the points
0, 1, 1/k, ∞, −1/k, −1 have the images 0, K, K + iK ′ , iK ′ , K − iK ′ , −K respectively.
The function sn x repeats in congruent blocks of four rectangles and, therefore, is
invariant under translations by ω 1 = 4K(k) and ω 3 = 2iK ′ (k). Here K and K ′ are
complete elliptic integrals (K ′ is called complementary)
K =
K ′ =
∫ 1
0
∫ 1/k
1
dy
√
(1 − y2 )(1 − k 2 y 2 )
∫
dy
1
√
(1 − y2 )(1 − k 2 y 2 ) =
where k = √ 1 − k 2 is the complementary modulus.
Writing
x =
∫ sn x
and differentiating over x we will get
0
1 =
dy
√
(1 − y2 )(1 − k 2 y 2 )
sn ′ x
√
(1 − y2 )(1 − k 2 y 2 )
0
dy
√
(1 − y2 )(1 − k ′2 y 2 ) ,
or
(sn ′ x) 2 = (1 − y 2 )(1 − k 2 y 2 ) .
This is differential equation satisfied by the Jacobi elliptic function sn x.
– 28 –