Diploma - Max Planck Institute for Solid State Research

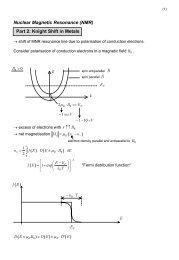
10 2 Theoretical foundation
Figure 2.2: muffin tin with pastries: the potential in LMTO is similar to a muffin tin devided
into two parts – a spherical symmetric Coulomb-like potential around the atomic sites and a
constant interstitial region. In difference to the general case of atomic sphere methods which
are based on fragmented potentials as well, the potential is not continuously differentiable, but
the basis functions can be defined in a more convenient manner.
core, semi-core and valence orbitals) the matrix equation 2.12 gets simplyfied –
whereat this classification is solely artificial governed by the required accuracy.
Inserting the Bloch ansatz into eq. 2.9 projected onto a Kohn-Sham orbitals yields
the secular equation
⎛
⎞
∑
⎜
⎝〈 0s ′ µ ′ | H | Bsµ 〉 − 〈 0s ′ µ ′ ⎟
| Bsµ 〉ɛ
} {{ } } {{ kn ⎠ c kn
}
Bsµ
(1)
(2)
sµ e ik(B+s−s′ ) !
= 0 (2.12)
with the Hamiltonian matrix (1) and the overlap matrix (2). This equation is now
solved iteratively.
All calculations based on this method are labelled as (fplo 9.07.41, parameters
and approximations used).
2. Linear Muffin Tin Orbital – Atomic Sphere Approximation code (LMTO-
ASA) [17, p. 331–333, p. 355–363]
The Muffin Tin Orbital [25] approach is a special case of an APW method employing
a spherically-symmetrized potential for the atomic part and a “flat” one
in the interstitial region 4 (see fig. 2.2) with a smart choice for the basis functions
– using surface spherical harmonics multiplied by
a) the radial solution plus a term proportional to the spherical Bessel function
(regular at the origin) inside the sphere and
4 comparable to the Korringa-Kohn-Rostoker[26, 27] method