Diploma - Max Planck Institute for Solid State Research

4.1 Overview – properties and classification 39
(a) FS: 33 (b) FS: 34 (c) FS: 35
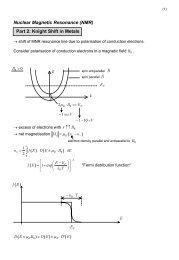
Figure 4.12: Fermi sheets (FS) of EuRh 2 Si 2 ; outer face is depicted in red, the inner face in
blue. They are probably not comparable to the “true” bulk Fermi sheets, if the 4f are in the
range of the Fermi level. The numbering of the eigenvalues (sorted) is arbitrary originated in the
distinction between valence and core orbitals (fplo 9.07.41, LDA, 4f 7 unpolarized open core).
the calculated 4 projected bulk band structure (red). The border of the BZ is marked by
white-dashed lines. Regarding the bulk Fermi surface (cf. fig. 4.12), one recognizes that
the isosurface projected along the [001] direction consists mainly of Fermi sheet 34 and
35 representing the connected square-like structure around Γ with a gap at the M-point.
Apparently, the intensities of the experimental bulk emuissions seem to be inverse to
the calculated ones for the first BZ, but similar to the calculation in the second BZ.
This points to selection rules (best seen at the BZ border in the measurement), which
probably can be simulated by means of a sophisticated PE model. As already mentioned
before, inside the bulk band gap around the M-point resides an electron-like SS at
the Si terminated surface. In the measurement, there seem to be two nested states,
whereas the calculation reproduces only one. But regarding the structures labelled
1a and 1b in fig. 4.11 one recognices that the second surface state (1b) is above the
Fermi level in the calculation, hence it does not (severely) contribute to the shown
isoenergy surface. The deviation can probably be explained by a surface relaxation,
because the distances of the topmost layers are usually smaller than the corresponding
bulk intervals (cf. fig. 4.6). Moreover, there is a lobe-like SB oriented from the Γ-point
towards the M-point at Si terminated surfaces which motivates the observed intensityvariation
around Γ in the first BZ. The nodal point of the surface state 2 in fig. 4.11 is
above the Fermi level for Si termination (a), but below for Eu termination (b), which is in
good agreement with the measurement depicted in fig. 4.8 despite of that the calculated
SS seems to be weaker at Eu terminated surfaces. This has a more technical than
physical reason since fixing the 4f occupation and treating these orbitals as open core,
one reduces the freedom to generate an asymmetry in charge density at the surface. For
4 The projection onto the surface BZ has been obtained by a superposition of isosurfaces perpendicular
to the z-axis of the BZ. A Gaussian was used for energy broadening, which has been chosen around
15 meV being in the order of magnitude of the integration interval chosen for the measured spectrum.
The two major Fermi sheets which contribute to the projected bulk band structure, are depicted
in fig. 4.12, FS 34 and FS 35.