Diploma - Max Planck Institute for Solid State Research

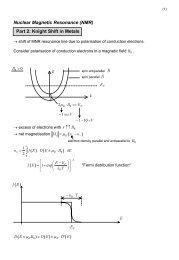
54 4 EuRh 2 Si 2 – semi-localized electrons
Figure 4.22: dispersion in X − Γ direction for different chosen k z . For k z = [0.0 − 0.285] · π/a x ,
there exists a band gap at Γ which closes at k z = 0.285 · π/a x being exactly the k-point where
a three-fold degenerate eigenenergy value near the Fermi level occurs in the Γ − Z dispersion
(cf. fig. 4.3). When the bands cross, a “Dirac Cone” seems to emerge. Going further to Z, the
band gap vanishes.
occurs at the surface. Similar states have been observed also in ironpnictides the groundstate
of which is metallic, hence it is an ongoing discussion whether the argumentation
made for insulators is transferable to intermetallics [80–82]. Many experimentally-based
publications claim, that there is a connection between the Dirac-like dispersion (microscopic
property) and transport (macroscopic property). The major difficulty in their
argumentations is the lacking knowledge of competing effects (e.g. impurity scattering,
magnetic order, correlation between different electronic subsystems) of such complex
systems. Therefore a short reasoning is given here, why it is worth to investigate the
origin of the linear dispersive state around Γ further and what investigations could be
done.
In fig. 4.21 the dispersion of the linear surface states for several cuts parallel to
k x are shown. It emphasizes a fourth-fold symmetry and there are evidences from
observed projected Fermi surfaces (not shown), that the quasi-Dirac cone is rather
deformed and that a section of the dispersion in the k x × k y plane can be regarded as a
superposition of two ellipsoids. The Fermi velocity amounts to (3.0±1.0) eV Å≈ 10 −3 ·c
[(2.5 ± 1.0) eV Å≈ 10 −3 · c] (c being the speed of light) for Si [Eu] termination which
is three times smaller than in graphene [83]. In the latter transport is dominated by
the Dirac cone but for intermetallics, since there are several bands intersecting the
Fermi level, it is not obvious and deserves a careful study.
As it has been demonstrated before (cf. ch. 4.1.4), the quasi-linear states seem to
be of surface origin. To explain their possible evolution, the bulk band structure is regarded
again. It reveals a three-fold degenerate eigenenergy value in going from Γ to Z
(cf. fig. 4.3) near the Fermi level, which evidences a rather steep slope in the Γ − M direction
(in bulk for example: Z−Γ 3 ). To examine this part further, different paths parallel
to the k x × k y plane are depicted in fig. 4.22 demonstrating the k z dispersion. For
k z = [0.0 − 0.285] · π/a x , there exists a band gap at Γ which closes at k z = 0.285 · π/a x .
Arriving at that plane, the degeneracy seems to force a linear dispersive behaviour
in the vicinity of k 1 = (0, 0, 0.285) · π/a x . Since the projected band structure for the