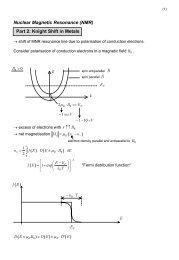
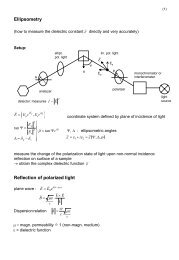
Diploma - Max Planck Institute for Solid State Research

4.1 Overview – properties and classification 29
the charge density a first time. Afterwards, the self-consistency cycle of the occupation
matrix has been permitted and the final result obtained. Returning to fig. 4.4, the
characteristica of this iterative process will be discussed. Fixing the occupation matrix
of the correlated orbital avoids shifting the orbital energies during the iterative process
due to the model Hamiltonian. Hence the eigenenergies of all 4f orbitals are located near
the Fermi level (red dotted representation). Allowing the fully self-consistent treatment
shifts the occupied (unoccupied) 4f orbitals below (above) the Fermi level, respectively
(blue dashed representation). Having 7 localized orbitals (spin degenerate) with an
occupation of 6.7, at least 3 should lie below the Fermi level (since their dispersion is
negligible). One can see, that for the self-consistent LDA+U calculation one 4f orbital
is 3 eV, one 2 eV below the Fermi level and two are around the Fermi level (being
partially above). Regarding regions marked by 1, it is apparent that the open core
approximation is suitable for the VB in an energy range not allocated by 4f orbitals.
In difference comparing 2a to 2b (being in the range of localized states), the symmetry
of the VB determines the hybridization strength, and thus the deviation from the open
core calculation. Therefore it is necessary to apply a hybridization model (see ch. 4.2)
to rearrange the band structure properly in the open core approximation (e.g. regarding
the Fermi surface of the compound).
4.1.3 Cleavage behaviour
As already mentioned in ch. 3, the surface is prepared in-situ by sample splitting, hence
the structure has several rupture lines (since it is layered). The lever stick has been
oriented in the [001] direction, so that we were able to measure the [001] surface BZ in
both setups (because k x , k y are equivalent and therefore the orientation of the entrance
slit does only matter for the type of polarization). To estimate the possible cleavage
plane and thus the atom type of the surface layer (termination) two different approaches
have been used:
(a) comparison of bond strength
The bond strength between the layers can be estimated by the “charge transfer”
inside the solid compared to the atomic allocation because electrons mediate bonds
which implies that the iso-charge density is a valid measure for their distribution.
Therefore the sum of the atomic charge densities (for each site) has been substracted
from the final (converged) charge density, so positive (negative) remaining charge
density corresponds to an inflow (outflow) of electrons. If one compares Fig. 4.5b
to fig. 4.5c it becomes evident, that the charge density is redistributed from the
Eu layer and the region between Eu and Si to the composition of Si-Rh-Si, mostly
between the atoms Rh-Si / Si-Rh, exactly in bonding direction. Thus the structural
integrity of the latter is larger than that of the Eu-Si bond and one expects either Si
or Eu terminated surfaces. Auxiliary, one can discuss the bonding type evaluating