Diploma - Max Planck Institute for Solid State Research

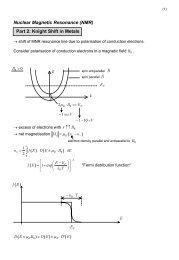
4.2 Hybridization: localized versus itinerant states 41
Figure 4.14: the orbital contributions to the band structure for the direction (0,0,0)-
(0,0.580·π/a x ,0) are shown illustrating the hybridization of the 4f levels in the LDA+U scheme.
The linear combinations of spherical harmonics with even m l [blue] do not mix in contrast to
the pairs (4f y(3x 2 −y 2 ), 4f yz 2) [red] and (4f xz 2, 4f x(x 2 −3y 2 )) [green] with odd m l (fplo 9.07.41,
LDA+U [AL], U = 8 eV, J = 1 eV). Red and green mark similar symmtries. The related linear
combinations of the complex spherical harmonics Y m l
l
are given.
4.2 Hybridization: localized versus itinerant states
To understand the phenomenology of the interactions between localized and itinerant
electrons, one needs on the one hand information on the hybridization strength and on
the other hand knowledge of the symmetry of coupling orbitals. We have already seen
in the LSDA+U calculation, that level crossings (allowed and avoided) are reproduced
in this scheme (cf. fig. 4.4) for both subsystems.
4.2.1 Symmetry considerations
Assuming that the chosen L(S)DA+U [AL] functional is more suitable than the pure
L(S)DA approximation, one can try to extract the symmetry from the former by a basis
transformation. To emphasize bonds in molecules, usually hybrid orbitals, so-called
molecular orbitals, are constructed. A similar transformation exists for Bloch bands
– the construction of Wannier Functions [58–60]. In principle, they are an orthogonal
basis set localized in real space and based on the Fourier transform of Bloch bands.
Since there is a gauge freedom of the Bloch phase, the definition of Wannier orbitals
is not unique. To elimenate the degree of freedom, one can choose maximally localized
Wannier functions (WFs) or another fixed construction principle [60]. Here, the