nr. 477 - 2011 - Institut for Natur, Systemer og Modeller (NSM)

More documents

Recommendations

Info

94 Bifurcation Diagrams and Analysis Figure 8.17 On the left we have the original five dimensional DuCa model, on the right the reduced three dimensional DuCa model. We see that despite some minor initial differences differences the curves are interchangeable. dM dt = a + (k + b)Ma − cM − f1MBa − e1M(M + Ma) (8.5) dMa dt = f1MBa − kMa − e2Ma(M + Ma) (8.6) dBa dt = W (t) + AmaxdBaMa kb(f1M + f2Ma) − f1MBa − f2MaBa − dBa (8.7) Figure 8.18 shows a bifurcation diagram of this reduced model with f1 as the bifurcation parameter. The similarities with figure 8.1 are striking, but this may not come as a surprise since the positions of the fixed points are expected to be the same because the QSS assumption of course holds in the fixed points. The real test is to see if the solution curves of M, Ma and Ba change under this assumption. As we can see in figure 8.17 there is not much difference, if any. But how else could we justify making a QSS assumption. The answer lies in the eigenvalues of the full system versus those of the reduced system. Let us digress to the example where we looked at the general solution to 7.2; given by equation 7.3. For the sake of argument let us assume that we have a two-dimensional system, and that both the eigenvalues are negative and not too different in magnitude. We know that in reality another component play a part in the behavior of system. Thus in reality we need an extra equation, which describes this extra component. At the same time we are aware that this makes the stability analysis more cumbersome. Thus we would like to know if it would be reasonable to make a QSS assumption on the extra equation, so we would be back in 2D land. To figure this out we add the extra equation, and take a look at the corresponding characteristic polynomial for the now three-dimensional system. If the new eigenvalue is significantly more negative than the others, then the solution curve associated with this eigenvalue will stabilize much faster than the two others. In fact the solution curve associated with this very negative eigenvalue will tend to the stable manifold spanned by the eigenvectors of the two other eigenvalues as an
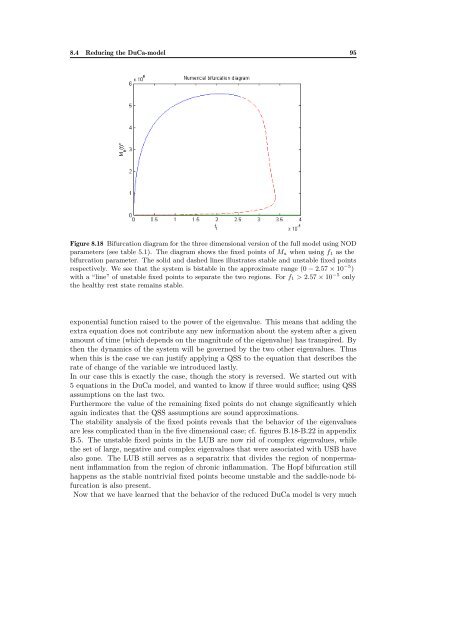
8.4 Reducing the DuCa-model 95 Figure 8.18 Bifurcation diagram for the three dimensional version of the full model using NOD parameters (see table 5.1). The diagram shows the fixed points of Ma when using f1 as the bifurcation parameter. The solid and dashed lines illustrates stable and unstable fixed points respectively. We see that the system is bistable in the approximate range (0 − 2.57 × 10 −5 ) with a “line” of unstable fixed points to separate the two regions. For f1 > 2.57 × 10 −5 only the healthy rest state remains stable. exponential function raised to the power of the eigenvalue. This means that adding the extra equation does not contribute any new information about the system after a given amount of time (which depends on the magnitude of the eigenvalue) has transpired. By then the dynamics of the system will be governed by the two other eigenvalues. Thus when this is the case we can justify applying a QSS to the equation that describes the rate of change of the variable we introduced lastly. In our case this is exactly the case, though the story is reversed. We started out with 5 equations in the DuCa model, and wanted to know if three would suffice; using QSS assumptions on the last two. Furthermore the value of the remaining fixed points do not change significantly which again indicates that the QSS assumptions are sound approximations. The stability analysis of the fixed points reveals that the behavior of the eigenvalues are less complicated than in the five dimensional case; cf. figures B.18-B.22 in appendix B.5. The unstable fixed points in the LUB are now rid of complex eigenvalues, while the set of large, negative and complex eigenvalues that were associated with USB have also gone. The LUB still serves as a separatrix that divides the region of nonpermanent inflammation from the region of chronic inflammation. The Hopf bifurcation still happens as the stable nontrivial fixed points become unstable and the saddle-node bifurcation is also present. Now that we have learned that the behavior of the reduced DuCa model is very much
Page 1 and 2:
- I, OM OG MED MATEMATIK OG FYSIK E
Page 3 and 4:
Exploring Treatment Strategies for
Page 5:
Preface iii questions that were out
Page 8 and 9:
vi Contents Significance of the Apo
Page 10 and 11:
List of Tables 5.1 summarizes the m
Page 12 and 13:
x List of Figures 8.3 Phase space p
Page 14 and 15:
xii
Page 16 and 17:
2 Introduction In the following dec
Page 18 and 19:
4 Introduction There are several sc
Page 20 and 21:
6 Introduction because I had to mak
Page 22 and 23:
8 Type 1 Diabetes and Its Etiology
Page 24 and 25:
10 Type 1 Diabetes and Its Etiology
Page 27 and 28:
3 Prospects for Therapy - A Mini Re
Page 29 and 30:
3.3 Gastrin 15 eration in situ Urus
Page 31 and 32:
4 Mathematical Modelling The langua
Page 33 and 34:
5 The DuCa Model In the following w
Page 35 and 36:
5.3 The DuCa Model - An Appetiser 2
Page 37 and 38:
5.4 The DuCa Model - Compartment Mo
Page 39 and 40:
Page 41 and 42:
Page 43 and 44:
5.6 Our Compartment Model 29 migrat
Page 45 and 46:
5.6 Our Compartment Model 31 a ✓
Page 47 and 48:
5.7 Discussion of Marée et al. (20
Page 49 and 50:
5.7 Discussion of Marée et al. (20
Page 51 and 52:
5.8 Discussion of Parameters 37 Fig
Page 53 and 54:
5.8 Discussion of Parameters 39 Par
Page 55 and 56:
5.8 Discussion of Parameters 41 tha
Page 57: 5.8 Discussion of Parameters 43 Fig
Page 60 and 61: 46 The Intermediated Model The diff
Page 62 and 63: 48 The Intermediated Model expected
Page 64 and 65: 50 The Intermediated Model Stabilit
Page 66 and 67: 52 The Intermediated Model restrict
Page 68 and 69: 54 The Intermediated Model We see t
Page 70 and 71: 56 The Intermediated Model paramete
Page 72 and 73: 58 The Intermediated Model ✻ Ma(t
Page 74 and 75: 60 The Intermediated Model 6.2 The
Page 76 and 77: 62 The Intermediated Model ✻ Ma(t
Page 79 and 80: 7 A Brief Introduction to Bifurcati
Page 81 and 82: 7.2 The Hopf bifurcation 67 the gen
Page 83 and 84: 7.3 Biological Relevance of Bifurca
Page 85: 7.5 Locating the Fixed Points 71 Ev
Page 88 and 89: 74 Bifurcation Diagrams and Analysi
Page 112 and 113: 98 Discussion of the Bifurcation An
Page 114 and 115: 100 Discussion of the Bifurcation A
Page 116 and 117: 102
Page 118 and 119: 104
Page 120 and 121: 106 Expanding and Modifying the DuC
Page 132 and 133: 118 Discussion of the Expanded Mode
Page 134 and 135: 120 Discussion of the Expanded Mode
Page 136 and 137: 122
Page 138 and 139: 124
Page 140 and 141: 126 Bibliography Christen, U. and M
Page 142 and 143: 128 Bibliography Notkins, A. L. and
Page 144 and 145: 130 Bibliography Yu, J. and G. S. E
Page 146 and 147: 132 Mathematical Appendices the com
Page 148 and 149: 134 Mathematical Appendices in that
Page 150 and 151: 136 Mathematical Appendices A.6 Dim
Page 152 and 153: 138
Page 154 and 155: 140 Additional Figures Figure B.2 P
Page 156 and 157: 142 Additional Figures B.2 Eigenval
Page 158 and 159:
144 Additional Figures Figure B.8 P
Page 160 and 161:
146 Additional Figures B.3 Eigenval
Page 162 and 163:
148 Additional Figures Figure B.14
Page 164 and 165:
Page 166 and 167:
152 Additional Figures B.5 Eigenval
Page 168 and 169:
Page 170 and 171:
Page 172 and 173:
158 matlab Code w(r+1)=w(r)+dw; g=w
Page 174 and 175:
160 matlab Code end V_11(r)=E(1); V
Page 176 and 177:
162 matlab Code n=675; w_5=0; dw_5=
Page 178 and 179:
164 matlab Code M=M’; % end s_7(r
Page 180 and 181:
166 matlab Code w_7,V_34,’.b’,w
Page 182 and 183:
168 matlab Code M=M’; % M must be
Page 184 and 185:
170 matlab Code %options = odeset(
Page 186 and 187:
172
Page 188 and 189:
174 Index value, 73 Bifurcation Ana
Page 190 and 191:
176 Index of diabetes, 2 Michaelis
show all

nr. 477 - 2011 - Institut for Natur, Systemer og Modeller (NSM)

Create successful ePaper yourself

Delete template?

Save as template?