nr. 477 - 2011 - Institut for Natur, Systemer og Modeller (NSM)

8.2 Using f1 as the bifurcation parameter 85
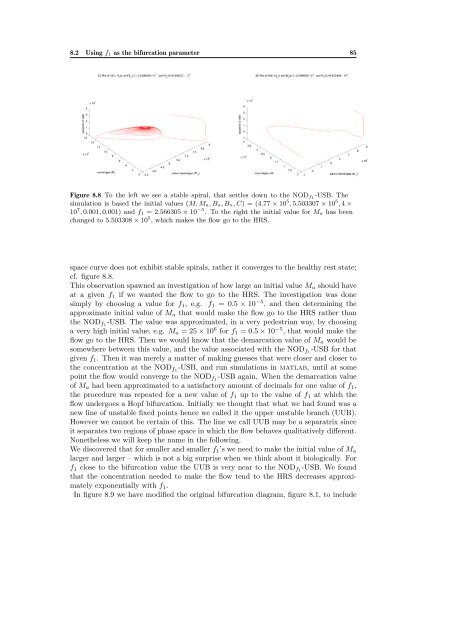
Figure 8.8 To the left we see a stable spiral, that settles down to the NODf1-USB. The
simulation is based the initial values (M, Ma, Ba, Bn, C) = (4.77 × 10 5 , 5.503307 × 10 5 , 4 ×
10 7 , 0.001, 0.001) and f1 = 2.566305 × 10 −5 . To the right the initial value for Ma has been
changed to 5.503308 × 10 5 , which makes the flow go to the HRS.
space curve does not exhibit stable spirals, rather it converges to the healthy rest state;
cf. figure 8.8.
This observation spawned an investigation of how large an initial value Ma should have
at a given f1 if we wanted the flow to go to the HRS. The investigation was done
simply by choosing a value for f1, e.g. f1 = 0.5 × 10 −5 , and then determining the
approximate initial value of Ma that would make the flow go to the HRS rather than
the NODf1-USB. The value was approximated, in a very pedestrian way, by choosing
a very high initial value, e.g. Ma = 25 × 10 6 for f1 = 0.5 × 10 −5 , that would make the
flow go to the HRS. Then we would know that the demarcation value of Ma would be
somewhere between this value, and the value associated with the NODf1-USB for that
given f1. Then it was merely a matter of making guesses that were closer and closer to
the concentration at the NODf1-USB, and run simulations in matlab, until at some
point the flow would converge to the NODf1-USB again. When the demarcation value
of Ma had been approximated to a satisfactory amount of decimals for one value of f1,
the procedure was repeated for a new value of f1 up to the value of f1 at which the
flow undergoes a Hopf bifurcation. Initially we thought that what we had found was a
new line of unstable fixed points hence we called it the upper unstable branch (UUB).
However we cannot be certain of this. The line we call UUB may be a separatrix since
it separates two regions of phase space in which the flow behaves qualitatively different.
Nonetheless we will keep the name in the following.
We discovered that for smaller and smaller f1’s we need to make the initial value of Ma
larger and larger – which is not a big surprise when we think about it biologically. For
f1 close to the bifurcation value the UUB is very near to the NODf1-USB. We found
that the concentration needed to make the flow tend to the HRS decreases approximately
exponentially with f1.
In figure 8.9 we have modified the original bifurcation diagram, figure 8.1, to include