CHAPTER 13 Simple Linear Regression
CHAPTER 13 Simple Linear Regression
CHAPTER 13 Simple Linear Regression
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
524 <strong>CHAPTER</strong> THIRTEEN <strong>Simple</strong> <strong>Linear</strong> <strong>Regression</strong><br />
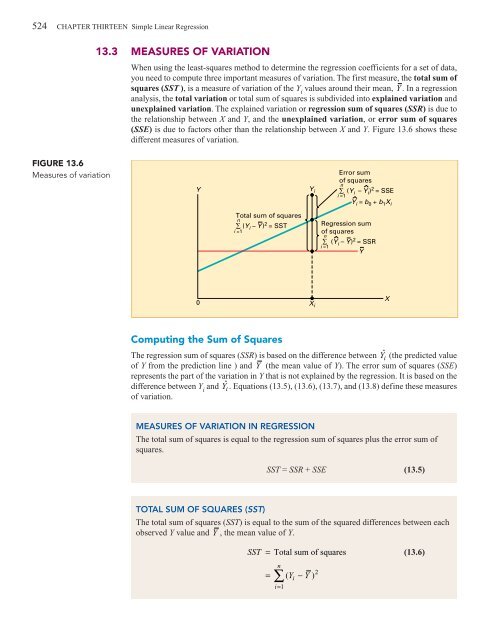
<strong>13</strong>.3 MEASURES OF VARIATION<br />
When using the least-squares method to determine the regression coefficients for a set of data,<br />
you need to compute three important measures of variation. The first measure, the total sum of<br />
squares (SST ), is a measure of variation of the Y i<br />
values around their mean, Y . In a regression<br />
analysis, the total variation or total sum of squares is subdivided into explained variation and<br />
unexplained variation. The explained variation or regression sum of squares (SSR) is due to<br />
the relationship between X and Y, and the unexplained variation, or error sum of squares<br />
(SSE) is due to factors other than the relationship between X and Y. Figure <strong>13</strong>.6 shows these<br />
different measures of variation.<br />
FIGURE <strong>13</strong>.6<br />
Measures of variation<br />
Y<br />
Y i<br />
Error sum<br />
of squares<br />
n<br />
∑ (Y i – Y i ) 2 = SSE<br />
i =1<br />
Y i = b 0 + b 1 X i<br />
Total sum of squares<br />
n<br />
∑ (Y i – Y) 2 = SST<br />
i =1<br />
<strong>Regression</strong> sum<br />
of squares<br />
n<br />
∑ (Y i – Y) 2 = SSR<br />
i =1<br />
Y<br />
0<br />
X i<br />
X<br />
Computing the Sum of Squares<br />
The regression sum of squares (SSR) is based on the difference between Yˆ<br />
i (the predicted value<br />
of Y from the prediction line ) and Y (the mean value of Y). The error sum of squares (SSE)<br />
represents the part of the variation in Y that is not explained by the regression. It is based on the<br />
difference between Y i<br />
and Yˆ<br />
i . Equations (<strong>13</strong>.5), (<strong>13</strong>.6), (<strong>13</strong>.7), and (<strong>13</strong>.8) define these measures<br />
of variation.<br />
MEASURES OF VARIATION IN REGRESSION<br />
The total sum of squares is equal to the regression sum of squares plus the error sum of<br />
squares.<br />
SST = SSR + SSE (<strong>13</strong>.5)<br />
TOTAL SUM OF SQUARES (SST)<br />
The total sum of squares (SST) is equal to the sum of the squared differences between each<br />
observed Y value and Y , the mean value of Y.<br />
SST<br />
= Total sum of squares<br />
n<br />
∑<br />
= ( Y −Y<br />
) 2<br />
i=<br />
1<br />
i<br />
(<strong>13</strong>.6)