sparse grid method in the libor market model. option valuation and the

grids with the largest multi-index value.
6.1.3 Greeks: Delta
In Chapter 2, we have discussed setting up a hedge portfolio Π t . It has been made
clear that finding a process ∆ t for holdings in an underlying is vital for being able to
replicate an option payoff. Derivatives in LIBOR Market Model, in this sense, belong
to a “multi-asset” type of products. Thus, with LIBOR rates as underlying assets, we
can denote:
∆ i = ∂U
∂L i
(6.1)
where ∆ i is option’s sensitivity to the change in a i-th forward rate. Has the final solution
been obtained, finding deltas with respect to one of the forward rates is straightforward.
With full-grid Finite Differences, delta values can be extracted directly from
the final mesh of points in the form of first derivatives. In case of sparse grids, it
is not possible to apply the same procedure to the combination result, due to the its
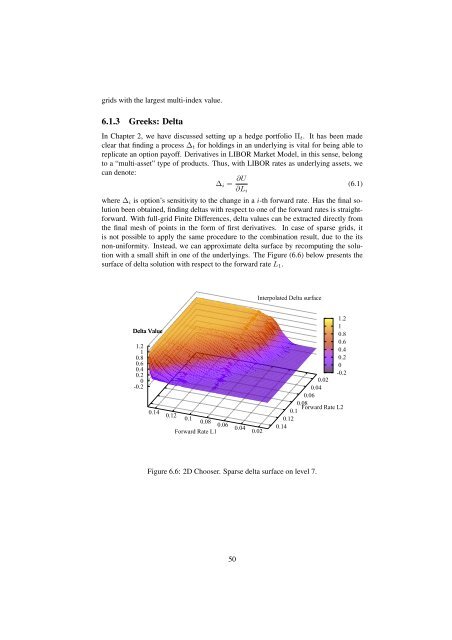
non-uniformity. Instead, we can approximate delta surface by recomputing the solution
with a small shift in one of the underlyings. The Figure (6.6) below presents the
surface of delta solution with respect to the forward rate L 1 .
Interpolated Delta surface
Delta Value
1.2
0.8 1
0.6
0.4
0.2
-0.2 0
0.14
0.12
0.1
0.08
0.06
Forward Rate L1
0.04
0.02
0.02
0.04
0.06
0.08
0.1
0.12
0.14
1.2
1
0.8
0.6
0.4
0.2
0
-0.2
Forward Rate L2
Figure 6.6: 2D Chooser. Sparse delta surface on level 7.
50