sparse grid method in the libor market model. option valuation and the
sparse grid method in the libor market model. option valuation and the
sparse grid method in the libor market model. option valuation and the
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
Remark. The way we impose boundary conditions, that is keep<strong>in</strong>g <strong>the</strong>m fixed or<br />
sett<strong>in</strong>g <strong>the</strong>m to Black-Scholes value, does make a difference when we look at extracted<br />
Delta profile. Yet, <strong>in</strong> both cases, <strong>the</strong> approximation is still not accurate enough to<br />
provide smooth surfaces on <strong>the</strong> Delta plot. Tak<strong>in</strong>g advantage of <strong>the</strong> fact that people<br />
are mostly <strong>in</strong>terested <strong>in</strong> <strong>the</strong> ∆’s <strong>in</strong> at-<strong>the</strong>-money or close to at-<strong>the</strong>-money states, <strong>the</strong><br />
disturbed boundaries were excluded from <strong>the</strong> plots above.<br />
6.1.4 Greeks: Vega<br />
∆ is just one of <strong>the</strong> several sensitivities that help explore exposure to risk <strong>in</strong> <strong>the</strong> short<br />
position as a function of different <strong>model</strong> parameters. O<strong>the</strong>r ’Greek letters’ <strong>in</strong>clude Θ<br />
with respect to time changes <strong>and</strong> Γ as <strong>the</strong> second derivative with respect to changes <strong>in</strong><br />
underly<strong>in</strong>g. In this part of <strong>the</strong> text we turn to vega, V, a sensitivity of a product with<br />
respect to <strong>the</strong> volatility <strong>in</strong> one of <strong>the</strong> underly<strong>in</strong>g forward rates:<br />
V = ∂U<br />
∂σ i<br />
(6.2)<br />
Information about V is not encapsulated <strong>in</strong> <strong>the</strong> solution explicitly. Here, whe<strong>the</strong>r full<br />
<strong>and</strong> <strong>sparse</strong>, <strong>the</strong> solution has to be recomputed with a small shift <strong>in</strong> volatility value of<br />
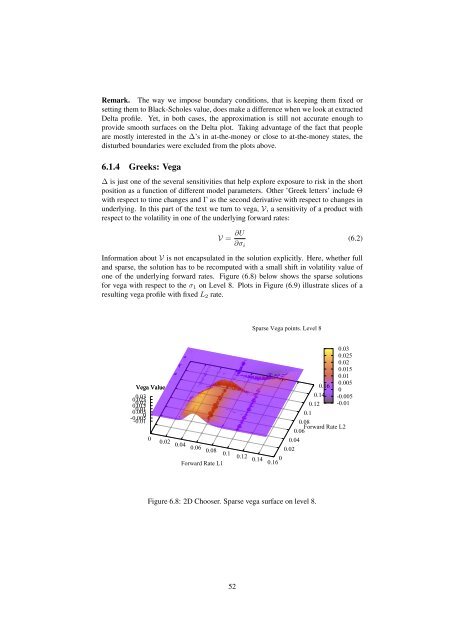
one of <strong>the</strong> underly<strong>in</strong>g forward rates. Figure (6.8) below shows <strong>the</strong> <strong>sparse</strong> solutions<br />
for vega with respect to <strong>the</strong> σ 1 on Level 8. Plots <strong>in</strong> Figure (6.9) illustrate slices of a<br />
result<strong>in</strong>g vega profile with fixed L 2 rate.<br />
Sparse Vega po<strong>in</strong>ts. Level 8<br />
Vega Value<br />
0.03<br />
0.025<br />
0.015<br />
0.02<br />
0.005<br />
0.01<br />
-0.005 0<br />
-0.01<br />
0<br />
0.02 0.04 0.06 0.08<br />
0.1 0.12 0.14 0.16<br />
0<br />
Forward Rate L1<br />
0.04<br />
0.02<br />
0.16<br />
0.14<br />
0.12<br />
0.03<br />
0.025<br />
0.02<br />
0.015<br />
0.01<br />
0.005<br />
0<br />
-0.005<br />
-0.01<br />
0.1<br />
0.08<br />
Forward Rate L2<br />
0.06<br />
Figure 6.8: 2D Chooser. Sparse vega surface on level 8.<br />
52