View - Universidad de Almería

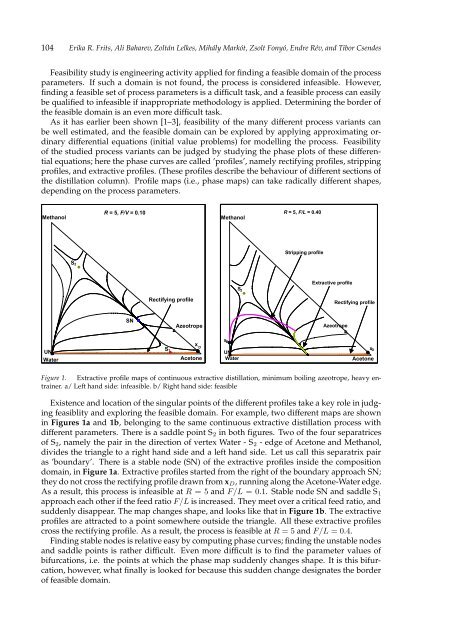
104 Erika R. Frits, Ali Baharev, Zoltán Lelkes, Mihály Markót, Zsolt Fonyó, Endre Rév, and Tibor CsendesFeasibility study is engineering activity applied for finding a feasible domain of the processparameters. If such a domain is not found, the process is considered infeasible. However,finding a feasible set of process parameters is a difficult task, and a feasible process can easilybe qualified to infeasible if inappropriate methodology is applied. Determining the border ofthe feasible domain is an even more difficult task.As it has earlier been shown [1–3], feasibility of the many different process variants canbe well estimated, and the feasible domain can be explored by applying approximating ordinarydifferential equations (initial value problems) for modelling the process. Feasibilityof the studied process variants can be judged by studying the phase plots of these differentialequations; here the phase curves are called ’profiles’, namely rectifying profiles, strippingprofiles, and extractive profiles. (These profiles describe the behaviour of different sections ofthe distillation column). Profile maps (i.e., phase maps) can take radically different shapes,depending on the process parameters.MethanolR = 5, F/V = 0.10MethanolR = 5, F/L = 0.40Stripping profileS 2S 2Extractive profileRectifying profileRectifying profileSNAzeotropeAzeotropex BUNWaterS 1x DAcetoneUNWaterx DAcetoneFigure 1. Extractive profile maps of continuous extractive distillation, minimum boiling azeotrope, heavy entrainer.a/ Left hand side: infeasible. b/ Right hand side: feasibleExistence and location of the singular points of the different profiles take a key role in judgingfeasiblity and exploring the feasible domain. For example, two different maps are shownin Figures 1a and 1b, belonging to the same continuous extractive distillation process withdifferent parameters. There is a saddle point S 2 in both figures. Two of the four separatricesof S 2 , namely the pair in the direction of vertex Water - S 2 - edge of Acetone and Methanol,divides the triangle to a right hand side and a left hand side. Let us call this separatrix pairas ’boundary’. There is a stable node (SN) of the extractive profiles inside the compositiondomain, in Figure 1a. Extractive profiles started from the right of the boundary approach SN;they do not cross the rectifying profile drawn from x D , running along the Acetone-Water edge.As a result, this process is infeasible at R = 5 and F/L = 0.1. Stable node SN and saddle S 1approach each other if the feed ratio F/L is increased. They meet over a critical feed ratio, andsuddenly disappear. The map changes shape, and looks like that in Figure 1b. The extractiveprofiles are attracted to a point somewhere outside the triangle. All these extractive profilescross the rectifying profile. As a result, the process is feasible at R = 5 and F/L = 0.4.Finding stable nodes is relative easy by computing phase curves; finding the unstable nodesand saddle points is rather difficult. Even more difficult is to find the parameter values ofbifurcations, i.e. the points at which the phase map suddenly changes shape. It is this bifurcation,however, what finally is looked for because this sudden change designates the borderof feasible domain.